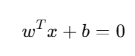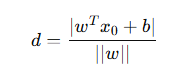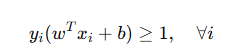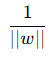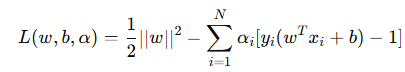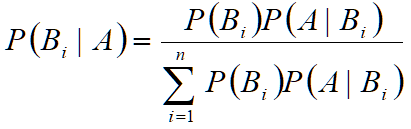1. 集合
集合分为有限集和无限集;
对于有限集,两集合元素数相等即为等势;
对于无限集,两集合元素存在一一映射关系即为等势;
无限集根据是否与正整数集等势分为可数集和不可数集。
2. sigmoid函数(也叫logistic函数)
公式:
含义:将实数集R映射到区间(0,1),两个区间是等势的,公式就是双射函数(一对一映射函数)。
3. 支持向量机
支持向量机的目标是寻找一个最优超平面,能够最大化分类间隔。
超平面形式:
数据到超平面的距离如下:
我们希望SVM在边界点数据(支持向量)的输出是
考虑上非边界点,输出是
我们最大化这个两个边界的距离的一半(支持向量到超平面的距离):
在这两个的约束下,即可求解最优w和b。
4. 决策树
1)信息论概念
信息量是事后的判断:指的是一个随机变量某个可能性(具体事件)发生所带来的信息,满足概率越低信息量越大、不相关事件信息量相加对应概率相乘,因此公式为:
𝐡(𝐱) = −𝒍𝒐𝒈𝟐𝒑(𝒙)
信息熵是事前的预估:指的是一个随机变量所有可能性的信息量的期望,公式为:
𝐇(𝐱) = −𝒔𝒖𝒎(𝒑(𝒙)𝒍𝒐𝒈𝟐𝒑(𝒙))
2)决策树理解
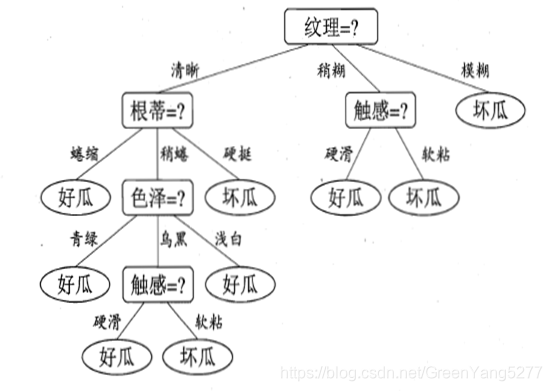
决策树是要找到一棵树,按照这棵树的节点进行递归判断就可以得到判断结果,例如一个瓜是不是好瓜,需要判断一系列特征然后得到结论。
决策树算法则是为了找到这样一颗树,需要确定节点顺序。显然应该优先判断重要特征,即那些对确定性增益最大的,或者说熵减最多的。
3)决策树实现
基于信息论的决策树算法有ID3 、C4.5和 CART等算法,其中C4.5和CART两种算法从ID3算法中衍生而来。
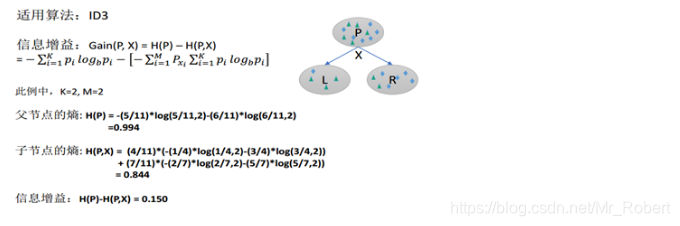
ID3算法使用 信息增益 作为分裂的规则,信息增益越大,则选取该分裂规则。具体来说,首先计算好瓜坏瓜这个随机变量的信息熵,然后计算特征A各个可能性下的好瓜坏瓜的信息熵的期望,相减得到信息增益,计算所有特征的信息增益,选取信息增益最大的作为节点。下一个节点则是在该特征的各个可能下继续上述操作来确定。
4)优缺点
| 优点 | 缺点 |
|---|---|
| 易于理解和解释 | 容易过拟合 |
| 能够处理多种数据类型 | 对数据分布敏感 |
| 对缺失值不敏感 | 倾向于选择具有更多取值的特征 |
| 不需要特征缩放 | 难以处理高维稀疏数据 |
| 能够捕捉非线性关系 | 不稳定性 |
| 计算效率较高 | 对类别不平衡数据敏感 |
| 支持分类和回归任务 | 难以表达复杂关系 |
5)改进方法
为了克服决策树的缺点,可以采用以下方法:
剪枝:通过预剪枝或后剪枝减少过拟合。
集成学习:使用随机森林(Random Forest)或梯度提升树(Gradient Boosting Trees)来提高模型的稳定性和泛化能力。
类别平衡处理:通过过采样、欠采样或调整类别权重来处理类别不平衡问题。
特征工程:对高维稀疏数据进行降维或特征选择。
6)剪枝处理
如果按照我们之前的方法形成决策树后,会存在一定的问题。决策树会无休止的生长,直到训练样本中所有样本都被划分到正确的分类。实际上训练样本中含有异常点,当决策树节点样本越少的时候,异常点就可能使得该结点划分错误。另外,我们的样本属性并不一定能完全代表分类的标准,可能有漏掉的特征,也可能有不准确的特征。这样就会导致决策树在训练集上准确率超高,但是在测试集上效果不好,模型过拟合,泛化能力弱。因此我们需要适当控制决策树的生长。
5. 朴素贝叶斯
1)贝叶斯公式
先验概率:通过经验来判断事情发生的概率
后验概率:事情发生后推测原因的概率
条件概率:一个事件在另一个事件发生条件下的概率,即P(B|A),若两者独立,则等于P(B)
全概率公式:P(Y) = P(Y,X1) + ... + P(Y,Xn) = P(X1)P(Y|X1) + ... + P(Xn)P(Y|Xn)
贝叶斯公式:
2)朴素贝叶斯(贝叶斯分类器)
朴素贝叶斯,假设每个输入变量之间独立。即全概率中各个X是独立的。
贝叶斯分类器就是在这种假设下的分类器,只需要求出在输入变量(特征)X1...Xn的条件下,各个可能类别的条件概率,找到最大的即为要分的类
贝叶斯分类器的参数(先验概率 P(c) 和条件概率 P(xi∣c))通常是通过一次训练过程计算得到的,不需要多轮训练。这是因为贝叶斯分类器的训练过程主要是基于训练数据来估计这些参数,而这些参数的估计通常是直接的统计计算,不需要像一些复杂的神经网络模型那样通过迭代优化来调整参数。
参考:【机器学习算法笔记系列】决策树(Decision Tree)算法详解和实战_decisiontreeclassifier是什么算法-CSDN博客