目录
目录
1.快速排序
1.1左右指针法
步骤:
- 建立一个keyi保存最左或者最右的下标,我这边选择的是最左(切记不要选择中间不好控制,反而使问题更复杂了);
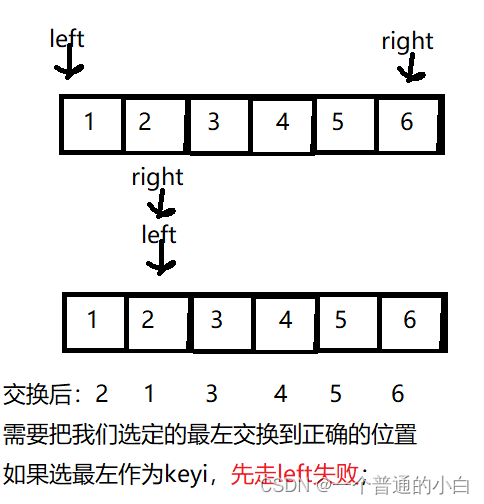
- 定义一个left和right,right从右向左找小,left从左向右找大(注:如果选择最左作为keyi,则需要right先走,left后走;选择最右同理);
如果选择left先走和我们需要的结果不同
3.right从右向左找小,如果找到比a[keyi]小的数则停下,再让left从左向右找大,找到比a[keyi]大的left停下,交换a[left]和a[right];然后继续以上过程,直到right和left相遇,出循环交换a[keyi]和相遇位置(left和right都可以)(单趟排序);
4.此时a[keyi]左边的数都小于a[keyi],右边大于的数都a[keyi];
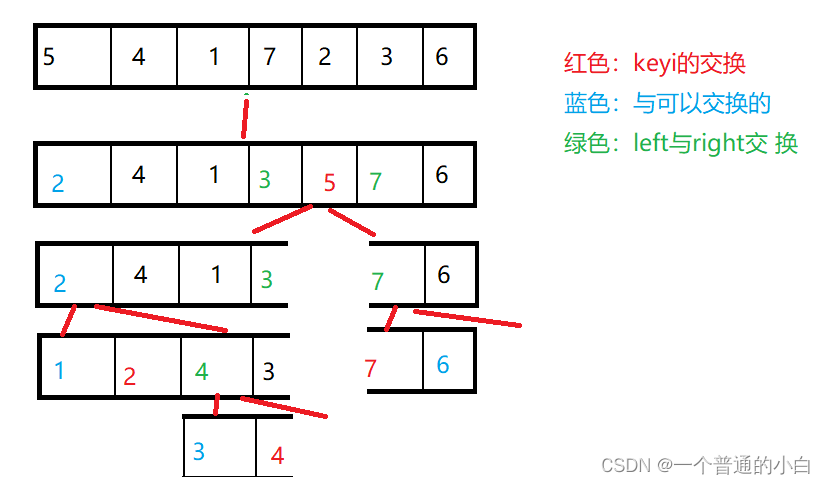
5.然后使用分治的思想,让keyi的左数列和右序列再次进行上面的单趟排序,反复此过程,直到左右数列只有一个数据或者不存在(使用递归);
如图所示:
代码如下:
int PartSort1(int* a, int left, int right)//左右指针法
{
int keyi = left;
while (right > left)
{
//一趟
while (right > left && a[right] >= a[keyi])//right>left以免越界
{
//找小
--right;
}
while (right > left && a[left] <= a[keyi])
{
//找大
left++;
}
Swap(&a[left], &a[right]);//交换或者相遇了交换还是没变
}
Swap(&a[keyi], &a[left]);//把key交换到正确的位置
return left;
}
void QuickSort(int* a, int begin, int end)//快速排序
{
if (begin >= end)
{
return;
}
//左子树[begin,meet-1]
//右子树[meet+1,end-1]
int meet = PartSort1(a, begin, end);
QuickSort(a, begin, meet - 1);
QuickSort(a, meet + 1, end);
}1.2挖坑法
步骤:
- 建立key保存最左或者最右,把此位置作为坑()
- 定义一个left和right,right从右向左找小,left从左向右找大(注:如果选择最左作为keyi,则需要right先走,left后走;选择最右同理)
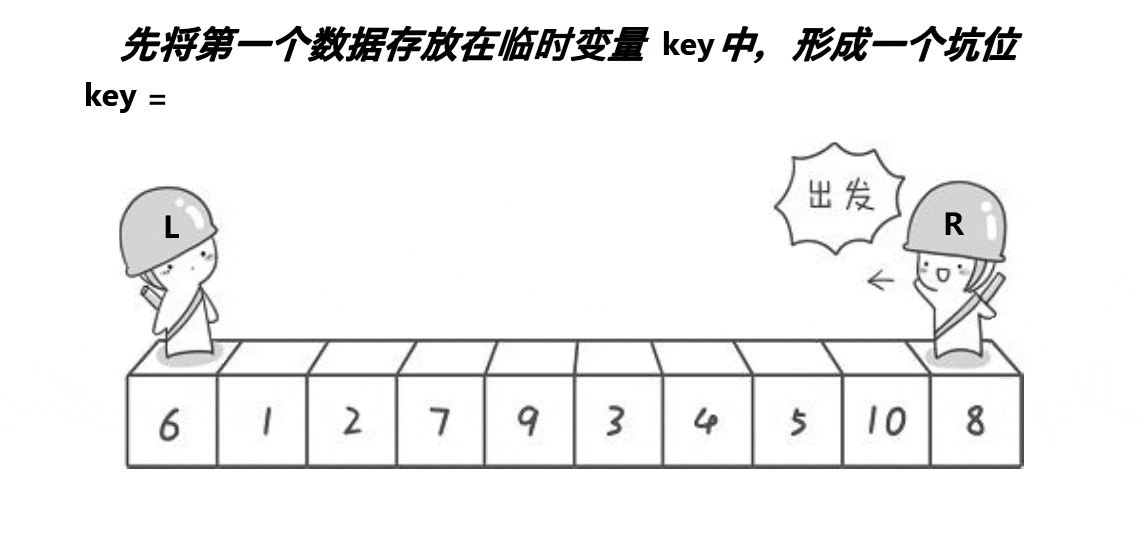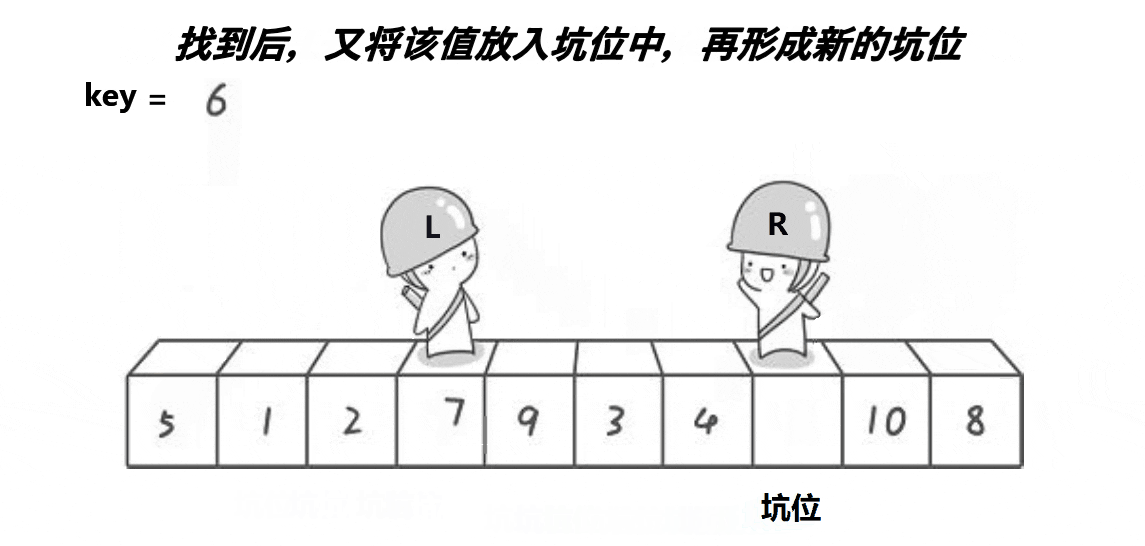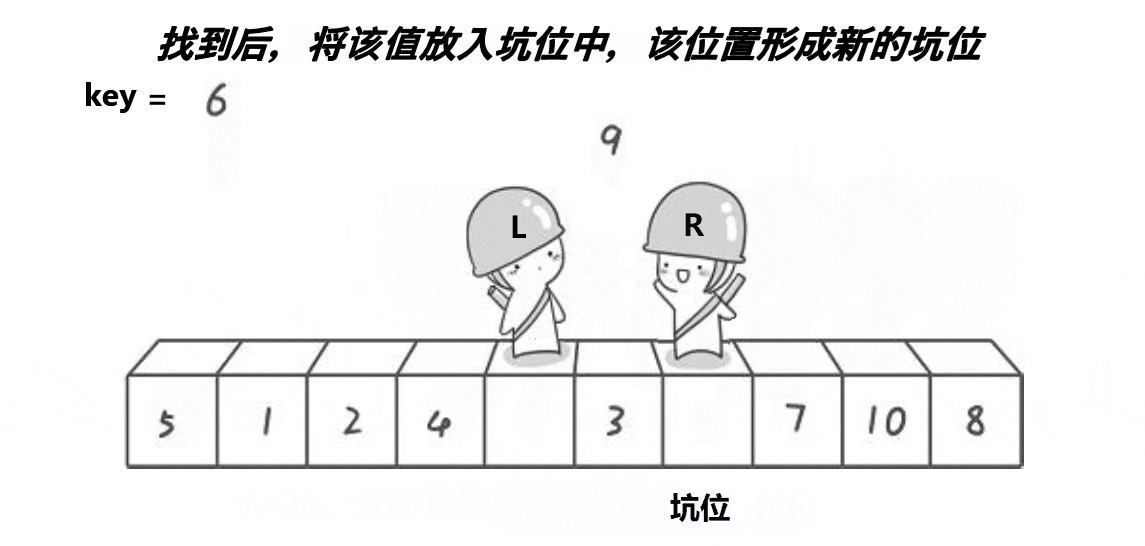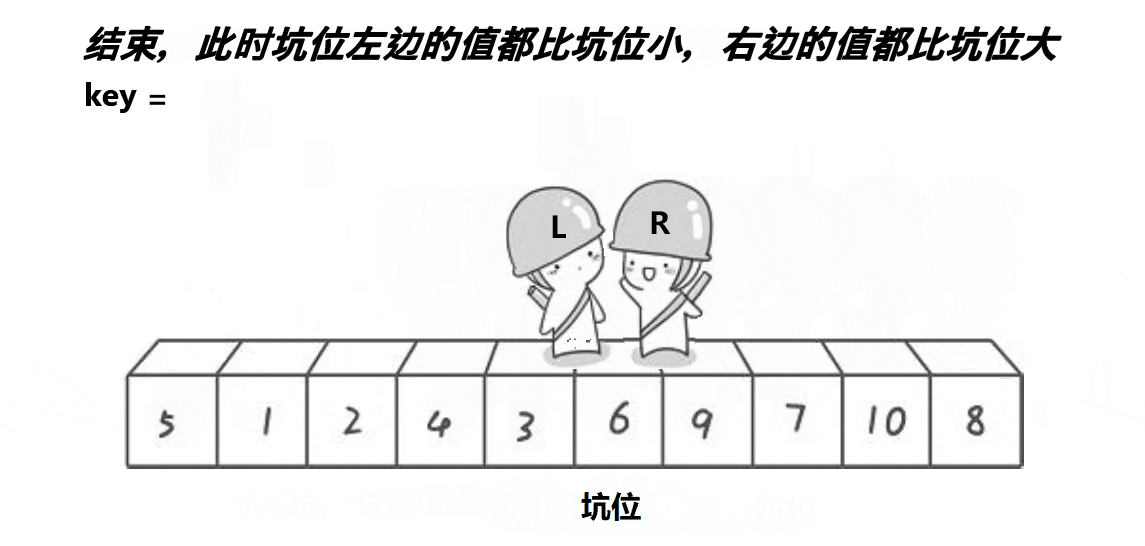
- right从右向左找小,如果找到比key小的数则停下,把a[right]放入坑中然后在a[right]位置形成新坑;再让left从左向右找大,找到比key大的left停下,把a[left]放入坑中然后在a[left]位置形成新坑;然后继续以上过程,直到right和left相遇,把key放入相遇的那个位置的坑(left和right都可以)(和左右指针法思路大体相同)(单趟排序);
-
此时key左边的数都小于key,右边大于的数都key;
-
然后使用分治的思想,让keyi的左数列和右序列再次进行上面的单趟排序,反复此过程,直到左右数列只有一个数据或者不存在(使用递归);
如图所示:
代码如图:
int PartSort2(int* a, int left, int right)//挖坑法
{
int key = a[left];
while (left < right)
{
//找小
while (left < right && a[right] >= key)
{
right--;
}
//把数放在左边的坑,右边形成新坑
a[left] = a[right];
//找大
while (left < right && a[left] <= key)
{
left++;
}
//把数放在右边的坑,左边形成新坑
a[right] = a[left];
}
//相遇了,把key放在相遇的坑
a[left] = key;
return left;
}
void QuickSort(int* a, int begin, int end)//快速排序
{
if (begin >= end)
{
return;
}
//左子树[begin,meet-1]
//右子树[meet+1,end-1]
int meet = PartSort2(a, begin, end);
QuickSort(a, begin, meet - 1);
QuickSort(a, meet + 1, end);
}1.3前后指针法
步骤:
- 建立一个keyi保存最左或者最右的下标,我这边选择的是最左(切记不要选择中间不好控制,反而使问题更复杂了);
- 定义一个前后指针cur和prev,prev=left,cut=prev+1(注:请在单趟排序中也要保持一前一后);
- cur从左到右找比a[keyi]小的数据,找到让prev++后交换a[prev]和a[cur],交换完成后cur++,重复以上过程直到cur>right(最后一个元素的下标),出循环交换a[prev]和a[key](单趟排序);
- 此时a[keyi]左边的数都小于a[keyi],右边大于的数都a[keyi];
- 然后使用分治的思想,让keyi的左数列和右序列再次进行上面的单趟排序,反复此过程,直到左右数列只有一个数据或者不存在(使用递归);
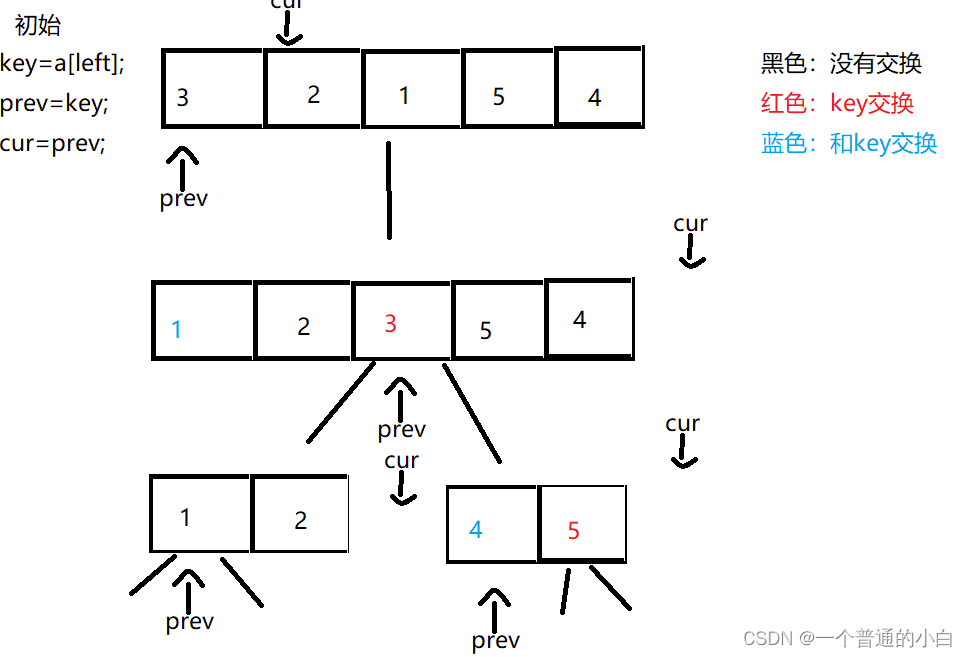
如图所示:
代码如图:
int PartSort3(int* a, int left, int right)//前后指针法
{
int keyi = left;
int prev = left, cur = prev + 1;
while (cur <= right)
{
while(cur <= right && a[cur] >= a[keyi])
{
cur++;
}
if (cur > right)
break;
Swap(&a[++prev], &a[cur]);
cur++;//保持perv和cur一前一后
//if(a[cur] < a[keyi] && ++prev != cur)//这个方法更简洁
//{
// Swap(&a[cur], &a[prev]);
//}
//cur++;
}
Swap(&a[keyi], &a[prev]);
return prev;
}
void QuickSort(int* a, int begin, int end)//快速排序
{
if (begin >= end)
{
return;
}
//左子树[begin,meet-1]
//右子树[meet+1,end-1]
int meet = PartSort3(a, begin, end);
QuickSort(a, begin, meet - 1);
QuickSort(a, meet + 1, end);
}1.4三数取中优化
思想:
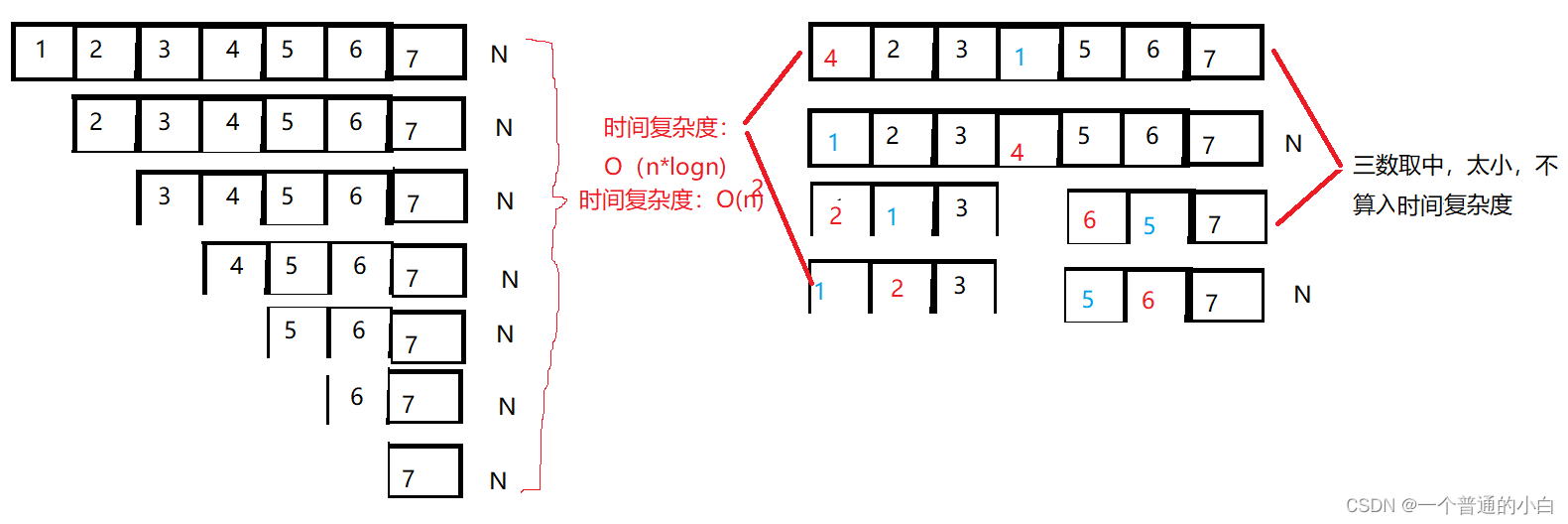
如果数组为一些极端情况(顺序),时间复杂度为O(n2),效率太低为了解决这种情况出现了三数取中,就是取头 ,尾,((头+尾)/2)的中位数,使快排的时间复杂度得到优化(三数取中很重要)
如图所示:
使用代码如图:
int GetMidIndex(int* a, int left, int right)//三数取中
{
int mid = (left + right) >> 1;
if (a[left] < a[mid])
{
if (a[mid] < a[right])
{
return mid;
}
else if(a[mid]>a[right])
{
if (a[left] > a[right])
{
return left;
}
else
{
return right;
}
}
}
else
{
if (a[mid] > a[right])
{
return mid;
}
else if (a[mid] < a[right])
{
if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
}
}
int PartSort1(int* a, int left, int right)//左右指针法
{
int midIndex = GetMidIndex(a, left, right);
Swap(&a[left], &a[midIndex]);
int keyi = left;
while (right > left)
{
//一趟
while (right > left && a[right] >= a[keyi])//right>left以免越界
{
//找小
--right;
}
while (right > left && a[left] <= a[keyi])
{
//找大
left++;
}
Swap(&a[left], &a[right]);//交换或者相遇了交换还是没变
}
Swap(&a[keyi], &a[left]);//把key交换到正确的位置
return left;
}