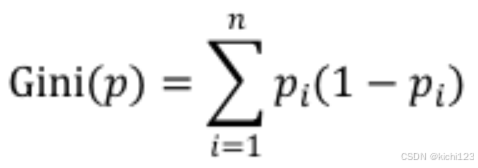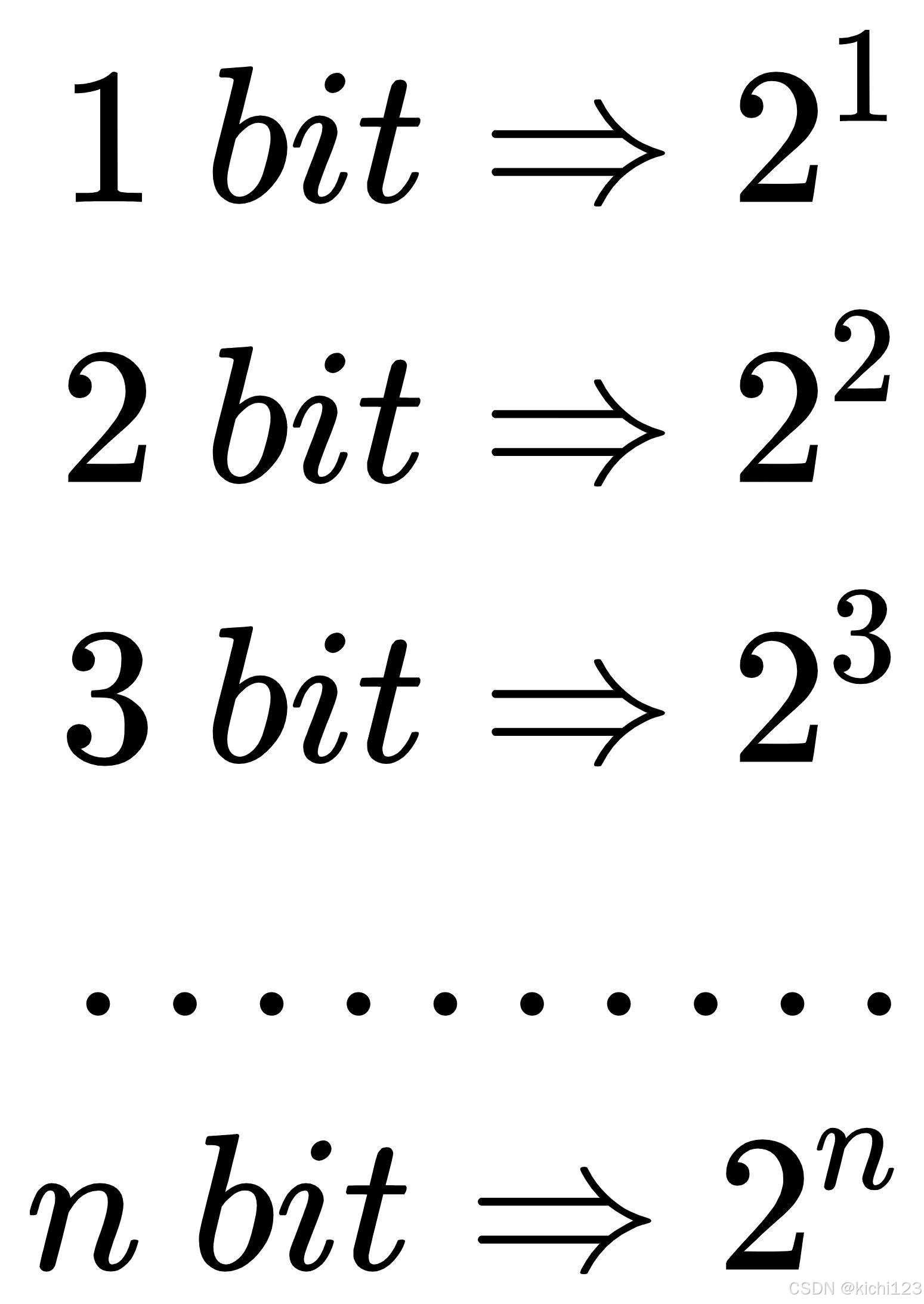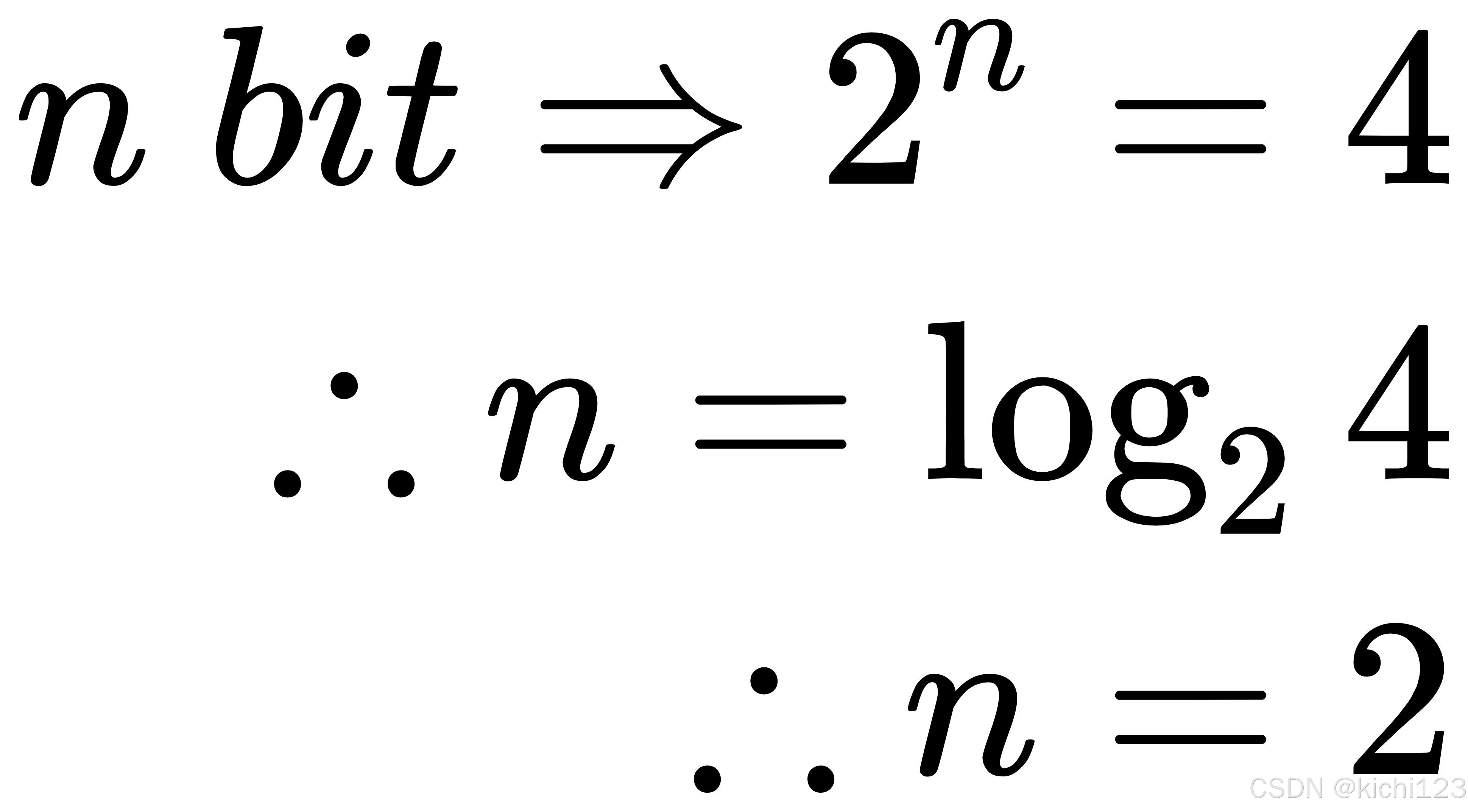目录
一、基本原理
1. 决策树的基本思想
决策树通过根据某种原则选择一个属性来划分数据集。例如,对于西瓜的分类问题,可能会先按照触感将西瓜划分,将“硬滑”与“软粘”属性的样本分成不同子集。接下来,对每个子集重复此划分过程,直到满足一定停止条件。这种递归划分的过程可以形成树形结构。
2. 决策树划分过程中可能遇到的特殊情况
(1) 单一类别终止:
当递归划分过程中某个子集中已仅含有同一类别的样本(如全为“好瓜”),则不再进行划分,直接终止该分支的划分过程。极端情况下,如果初始数据集中样本都属于同一类,则不进行任何划分。
(2) 属性用尽:
每次划分时,选择的属性通常不可重复使用(针对离散属性)。如果在递归过程中所有属性已被用尽,但子集内仍存在不同类别的样本,只能使用“少数服从多数”的原则,将样本数量最多的类别作为该子集的标签。即便属性集合未完全为空,当子集中样本在剩余属性上的取值相同时,也无法再继续划分,此时返回标记。
(3) 样本空缺:
若选择某一属性划分时,某个属性值没有对应的样本。例如,使用“纹理”属性划分,发现样本集中没有“模糊”取值的样本,此时该分支记为叶节点,并标记为训练集中出现频率最高的类别。这样可以为测试时可能遇到的样本提供一个默认分类。
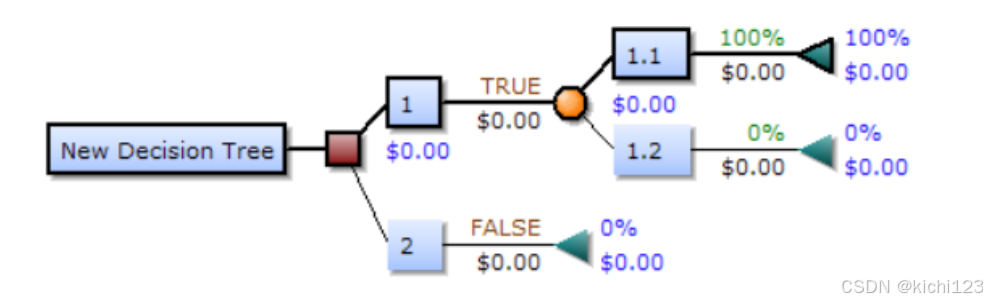
3. 决策树的结构
- 决策节点:通常用矩形框表示,代表数据集划分的属性。
- 机会节点:通常用圆圈表示,表示一种可能的属性值。
- 终结节点:通常用三角形表示,代表划分终止后的类别。
二、信息量、信息熵
首先可以看这个科普视频了解:如何理解信息熵_哔哩哔哩_bilibili
1. 信息量
信息量,字面理解是信息含量,没错,信息的多少也是可以度量的。对计算机有点了解的同学应该知道,计算机中存储信息容量的单位是b、Kb、Mb等,最小单位是bit,1b=8bit。
这里可以引用一个有点数学之美的解释方法来理解一下信息量的概念。
举个例子,我们现在有个事件A(四季),他是某种季节的可能性是1/4,那么也就是说,事件A总共有4种情况会发生,那么如果在计算机里要存储事件A,我们知道计算机里存储信息,1个bit有0和1共2种可能,即:
以此类推2 bit,3 bit……n bit:
那么对于四季这个有4种情况的事件,信息量是多少bit呢?
则"四季"这个事件的信息量为2bit。也就是说,我们得出一个信息量的表达公式,信息量:
2. 信息熵
信息熵用来度量一组数据的纯度,或者叫做复杂度、事件中包含了多少信息,从这个定义上,可以体会信息熵H(x)的表达式:
三、决策树
在构建决策树时,我们主要通过不纯度来决定划分的属性。经典的不纯度指标包括三种:信息增益(ID3算法)、信息增益率(C4.5算法)以及基尼指数(CART算法)。这些指标用于衡量节点划分后数据纯度的提升程度,以便更好地分类数据。
1. ID3 决策树(使用信息增益)
信息增益是知道了某个条件后,事件的不确定性下降的程度。写作 g(X,Y)。它的计算方式为熵减去条件熵:,表示的是,知道了某个条件后,原来事件不确定性降低的幅度。
2. C4.5 决策树(使用信息增益率)
假如某个条件极其严格,比如某个同学提前知道了所有选题的答案,那么将选题的序号作为条件,不存在任何不确定性,所以可以得到最大的信息增益。但是这个条件是没有意义的,假设老师换一份考卷答案就全部作废了。信息增益率在信息增益的基础上增加了惩罚项,惩罚项是特征的固有值,是避免上述情况而设计的。
写作gr (X,Y),定义为信息增益除以特征的固有值: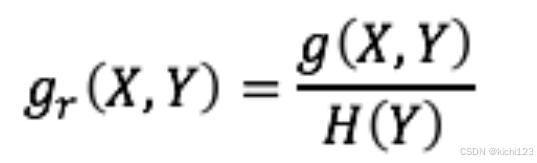
3. CART 决策树(使用基尼指数)
与熵一样,基尼系数表征的也是事件的不确定性,将熵定义式中的“logpi”替换为 1-pi 就是基尼系数: