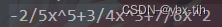数据结构实验一

哈尔滨工业大学计算学部

实验报告

课程名称：数据结构与算法

实验项目：线性表的链式存储结构与应用

实验题目：一元多项式计算器

一、实验目的

一元多项式计算器，使用链式存储结构实现计算，并且可以实现以下内容：

多项式的系数以分数形式表示，每一项的幂次可以用负数表示。
可以按任意顺序输入多项式并按照指数降幂的顺序输出。
计算过程中多项式的输入和输出通过文件进行。
可以计算两个多项式的加，减，和乘。
可以计算一元多项式的任意阶导数。
可以计算多项式在某一点的值，该未知数可为浮点数。

二、实验要求及实验环境

实验要求：

以动态或者静态链表存储一元多项式，在此基础上按要求完成对一元多项式的运算。（为保证多项式的值的准确性，多项式的系数可以用分数表示，涉及到两个分数相除时，结果也可以用分数表示。）

实验环境：

我本次使用Visual Studio Code来编写C++程序。

三、设计思想（本程序中的用到的所有数据类型的定义，主程序的流程图及各程序模块之间的调用关系、核心算法的主要步骤）

1．所使用的数据结构：

使用结构体来存储每一项，并通过链表形式来存储，结构体成员中定义了系数的分子coef1，分母coef2，指数exp，及指向下一项的指针link。

算法设计逻辑及程序运行效果：

（1）int main()

在main函数中打开并按照格式一项一项读入文件中的多项式

以下为输入文件：

排好序后，通过在控制台输入要进行的计算：

add 1 minus 2 mul 3 derivative 4 value 5

完成各项功能并在最后释放内存。

（2）polypointer CreatLNode(int coef1, int coef2, int exp)

用于在从文件中按照系数分子，系数分母，指数格式读出三个数据后，将这三个数据存储到一个结构体中，并返回指向该结构体的指针。

（3）void Insert(polypointer *head, polypointer p)

用于将结点p接入到头指针为head的链表的最后位置，判断头结点是否为空，若为空则该结点p为头结点，否则通过while循环找到该链表的最后一个结点，并在该结点的下一个结点插入p，并返回插入p结点后链表的头指针head。

（4）void Output(polypointer head, const char *filename)

该函数用于将链表头指针为head的链表输出到文件名为filename的文件中，首先判断是否能正确打开待写入文件，如果可以，为了正确输出多项式，保证第一项如果为正的则不输出正号，而项与项之间正常输出正负号，设置flag这一标志来判断是否为多项式的第一项，之后按照格式一项一项的输出到文件中。

（5）polypointer SortList(polypointer head)

用于对按照任意顺序输入的多项式按照指数幂次递降的顺序进行排序，如果待排序链表为空或者只有一项则无需进行排序，设置已排序部分的头结点和待排序部分的当前节点，当待排序链表的当前结点不为空即未排序结束，如果已排序链表头结点为空，即未进行排序或者待排序链表的当前结点指数大于排好序的第一项，这两种情况都需要在排序链表的头部插入该项，否则，找到合适顺序位置再插入。

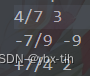
如下图为按照指数幂次递降顺序排好的两个多项式在文件中的输出。

（6）polypointer Derivate(polypointer head, int k)

该函数用于对多项式进行求任意阶导，首先用一个指针指向待求导的头指针，当当前待求导指针不为空即求导未进行完，在求导过程中需要注意如果此时指数为0，不应该把指数乘到系数上，按照流程进行求导直到完成k阶求导，再进行下一项的求导计算。下图为两个多项式完成求导后的结果输出到文件中的图。

（7）polypointer Add(polypointer a, polypointer b)

该函数用于求两个多项式的和，首先用两个指针分别指向两个多项式的头结点，当两个多项式都不为空时，申请一个临时节点temp，之后比较两个指针分别指向的多项式当前项的指数，如果不相等，则将较大的一项的指数，系数分子及分母分别赋值给temp，再将该结点追加到结果多项式相应的位置。如果相等，则判断两项系数之和是否为零，若为零，则略过这两项，否则赋值给temp接到结果多项式后面，再进行下一项的比较，直到其中一个多项式指针为空，则将另一个多项式剩余的全部接到结果多项式后面。下图为按照指数降幂次序输出的结果多项式文件中的内容。

对于减法来说，只需要把系数的分子变成相反数，直接执行Add函数即可。

（8）polypointer Mul(polypointer p1, polypointer p2)

该函数用于计算两个多项式相乘，对于多项式p1和多项式p2，令p，q分别指向p1和p2，p所指结点不为空时，将p当前所指结点与q的每一项相乘，并将结果插入到结果多项式中，之后p指向p1多项式的下一节点，再将该项与q的每一项相乘，接入结果多项式，直到p为空。下图为两个多项式相乘结果输出到文件的截图。

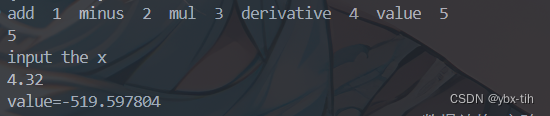
（9）double Value(double x, polypointer head)

该函数用于计算多项式求值，对于每一项，求出当取x值时的值，再将每一项的值加到一起。下图为控制台输出的结果。

四、测试结果

已在第三部分结合函数介绍给出运行截图。

五、经验体会与不足

通过此次实验的练习我更加熟悉链表的操作，并且发现了之前学习链表上的漏洞，并且由于程序代码较多，存在“牵一发而动全身”的情况，我认识到先有一个整体架构再填充细节的重要性，每修改一个地方都应注意是否会影响程序的其它部分。以下简要描述实验中遇到的问题：

初步完成代码后发现存在传了指针但是未能改变值的情况，与同学讨论发现传递指针是不能改变整个链表的，需要通过传递指针的地址或者将指针作为返回值返回来修改。

附录：源代码（带注释）

函数解释等注释已在上述部分给出。

#include <iostream>
#include <math.h>
struct polynode
{
    int coef1;
    int coef2;
    int exp;
    polynode *link;
};
typedef polynode *polypointer;

char Compare(int a, int b);
polypointer CreatLNode(int coef1, int coef2, int exp);
void Insert(polypointer *head, polypointer p);
polypointer SortList(polypointer head);
void Output(polypointer head, const char *filename);
polypointer Add(polypointer a, polypointer b);
void Reverse(polypointer head);
polypointer Mul(polypointer p1, polypointer p2);
polypointer Derivate(polypointer head, int k);
double Value(double x, polypointer head);

int main()
{
    polypointer head1 = NULL;
    polypointer head2 = NULL;
    int coef1, coef2, exp;
    FILE *file1;
    FILE *file2;
    int choice;

    if ((file1 = fopen("input1.txt", "r")) == NULL)
    {
        printf("Fail to open file1\n");
        exit(0);
    }
    if ((file2 = fopen("input2.txt", "r")) == NULL)
    {
        printf("Fail to open file2!\n");
        exit(0);
    }

    while (fscanf(file1, "%d/%d %d", &coef1, &coef2, &exp) == 3)
    {
        polypointer newLNode = CreatLNode(coef1, coef2, exp);
        Insert(&head1, newLNode);
    }
    while (fscanf(file2, "%d/%d %d", &coef1, &coef2, &exp) == 3)
    {
        polypointer newLNode = CreatLNode(coef1, coef2, exp);
        Insert(&head2, newLNode);
    }
    fclose(file1);
    fclose(file2);
    head1 = SortList(head1);
    head2 = SortList(head2);
    Output(head1, "output1.txt");
    Output(head2, "output2.txt");

    printf("add  1  minus  2  mul  3  derivative  4  value  5\n");
    scanf("%d", &choice);
    if (choice == 1)
    {
        polypointer result = Add(head1, head2);
        Output(result, "Add.txt");
    }
    else if (choice == 2)
    {
        Reverse(head2);
        polypointer result = Add(head1, head2);
        Output(result, "Minus.txt");
    }
    else if (choice == 3)
    {
        polypointer result = Mul(head1, head2);
        Output(result, "Mul.txt");
    }
    else if (choice == 4)
    {
        int k;
        printf("taking the nth derivative\n");
        scanf("%d", &k);
        head1 = Derivate(head1, k);
        head2 = Derivate(head2, k);
        Output(head1, "Derivate1.txt");
        Output(head2, "Derivate2.txt");
    }
    else if (choice == 5)
    {
        double x;
        double result = 0.0;
        printf("input the x\n");
        scanf("%lf", &x);
        result = Value(x, head1);
        printf("value=%f\n", result);
    }

    return 0;
}

char Compare(int a, int b)
{
    if (a > b)
        return '>';
    else if (a == b)
        return '=';
    else
        return '<';
}

polypointer CreatLNode(int coef1, int coef2, int exp)
{
    polypointer p = new polynode;
    if (p == NULL)
    {
        printf("no enough space");
        return NULL;
    }
    else
    {
        p->coef1 = coef1;
        p->coef2 = coef2;
        p->exp = exp;
        p->link = NULL;
        return p;
    }
}

void Insert(polypointer *head, polypointer p)
{
    if (*head == NULL)
        *head = p;
    else
    {
        polypointer q = *head;
        while (q->link != NULL)
            q = q->link;
        q->link = p;
    }
}

polypointer SortList(polypointer head)
{
    if (head == NULL || head->link == NULL)
        return head;
    polypointer sorted = NULL;
    polypointer current = head;
    while (current != NULL)
    {
        polypointer next = current->link;
        if (sorted == NULL || current->exp > sorted->exp)
        {
            current->link = sorted;
            sorted = current;
        }
        else
        {
            polypointer temp = sorted;
            while (temp->link != NULL && temp->link->exp > current->exp)
                temp = temp->link;
            current->link = temp->link;
            temp->link = current;
        }
        current = next;
    }
    return sorted;
}

void Output(polypointer head, const char *filename)
{
    FILE *file;
    if ((file = fopen(filename, "w")) == NULL)
    {
        printf("Fail to open file!!\n");
        exit(0);
    }
    else
    {
        polypointer p = head;
        int flag = 1;
        while (p)
        {
            if (flag == 1)
            {
                fprintf(file, "%d/%dx^%d", p->coef1, p->coef2, p->exp);
                p = p->link;
                flag = 0;
            }
            else
            {
                fprintf(file, "%+d/%dx^%d", p->coef1, p->coef2, p->exp);
                p = p->link;
            }
        }
    }
    fclose(file);
}

polypointer Add(polypointer a, polypointer b)
{
    polypointer qa = a;
    polypointer qb = b;
    polypointer result = NULL;
    polypointer temp = NULL;
    while (qa && qb)
    {
        temp = new polynode;
        switch (Compare(qa->exp, qb->exp))
        {
        case '>':
        {
            temp->coef1 = qa->coef1;
            temp->coef2 = qa->coef2;
            temp->exp = qa->exp;
            temp->link = NULL;
            if (result == NULL)
                result = temp;
            else
            {
                polypointer p = result;
                while (p->link != NULL)
                    p = p->link;
                p->link = temp;
            }
            qa = qa->link;
            break;
        }
        case '=':
        {
            temp->coef1 = qa->coef1 * qb->coef2 + qa->coef2 * qb->coef1;
            temp->coef2 = qa->coef2 * qb->coef2;
            temp->exp = qa->exp;
            temp->link = NULL;
            if (temp->coef1 != 0)
            {
                if (result == NULL)
                    result = temp;
                else
                {
                    polypointer p = result;
                    while (p->link != NULL)
                        p = p->link;
                    p->link = temp;
                }
            }
            qa = qa->link;
            qb = qb->link;
            break;
        }
        case '<':
        {
            temp->coef1 = qb->coef1;
            temp->coef2 = qb->coef2;
            temp->exp = qb->exp;
            temp->link = NULL;
            if (result == NULL)
                result = temp;
            else
            {
                polypointer p = result;
                while (p->link != NULL)
                    p = p->link;
                p->link = temp;
            }
            qb = qb->link;
            break;
        }
        }
    }
    while (qa)
    {
        polypointer a = new polynode;
        a->coef1 = qa->coef1;
        a->coef2 = qa->coef2;
        a->exp = qa->exp;
        a->link = NULL;
        Insert(&result, a);
        qa = qa->link;
    }
    while (qb)
    {
        polypointer a = new polynode;
        a->coef1 = qb->coef1;
        a->coef2 = qb->coef2;
        a->exp = qb->exp;
        a->link = NULL;
        Insert(&result, a);
        qb = qb->link;
    }
    return result;
}

void Reverse(polypointer head)
{
    polypointer p = head;
    while (p)
    {
        p->coef1 = -p->coef1;
        p = p->link;
    }
}

polypointer Mul(polypointer p1, polypointer p2)
{
    polypointer p = p1;
    polypointer q = p2;
    polypointer result1 = NULL;
    polypointer result2 = NULL;
    while (p)
    {
        q = p2;
        result1 = NULL;
        while (q)
        {
            polypointer temp = new polynode;
            temp->coef1 = p->coef1 * q->coef1;
            temp->coef2 = p->coef2 * q->coef2;
            temp->exp = p->exp + q->exp;
            temp->link = NULL;
            Insert(&result1, temp);
            q = q->link;
        }
        result2 = Add(result1, result2);
        p = p->link;
    }
    return result2;
}

polypointer Derivate(polypointer head, int k)
{
    polypointer result = head;
    polypointer p = result;
    if (result == NULL)
        return NULL;
    while (p)
    {
        int i = 1;
        while (i <= k)
        {
            if (p->exp != 0)
                p->coef1 = p->coef1 * p->exp;
            p->exp--;
            i++;
        }
        p = p->link;
    }
    return result;
}

double Value(double x, polypointer head)
{
    double result = 0.0;
    polypointer p = head;
    while (p)
    {
        double temp = (double)p->coef1 / (double)p->coef2 * pow(x, p->exp);
        result += temp;
        p = p->link;
    }
    return result;
}

数据结构实验一

悦读