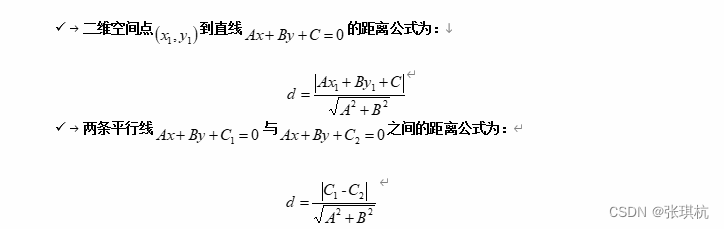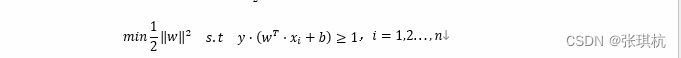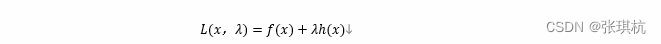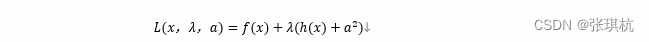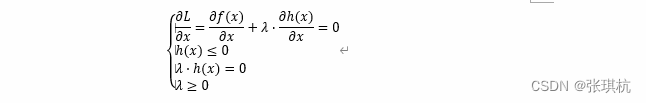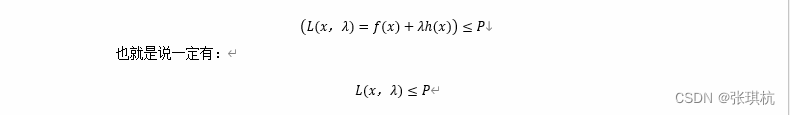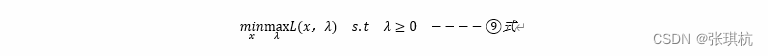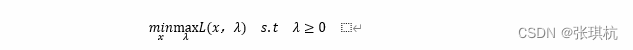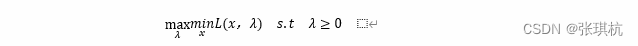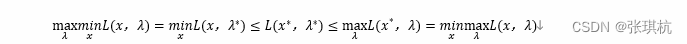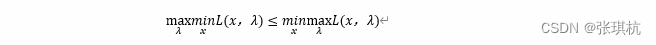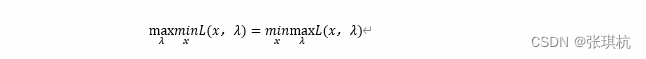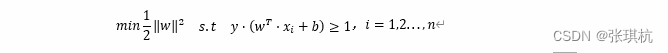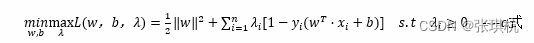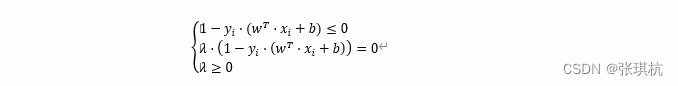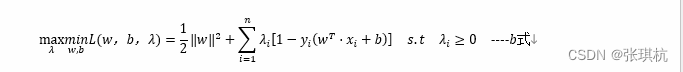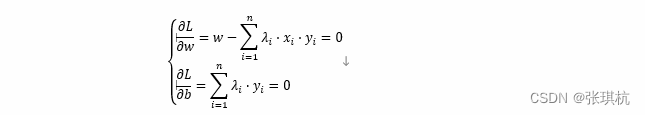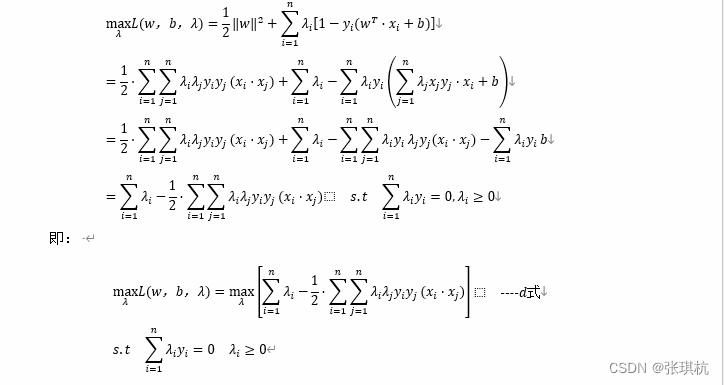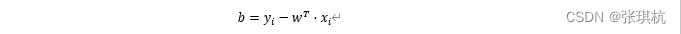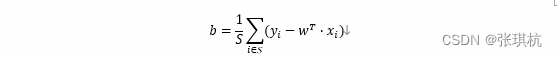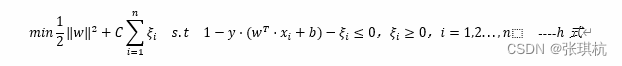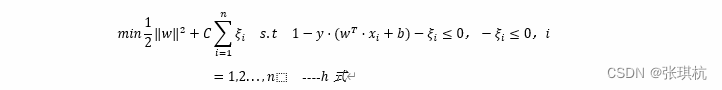目录
一支持向量机
1.支持向量机SVM
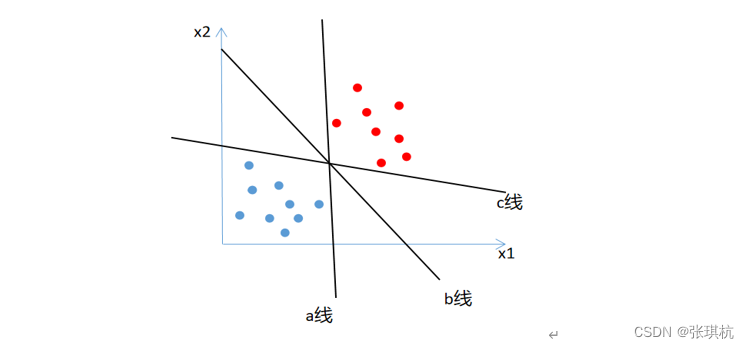
支持向量机(support vector machines,SVM)是一种二分类算法,它的目的是寻找一个超平面来对样本进行分割,分割的原则是间隔最大化,如果对应的样本特征少,一个普通的SVM就是一条线将样本分隔开,但是要求线到两个类别最近样本点的距离要最大。
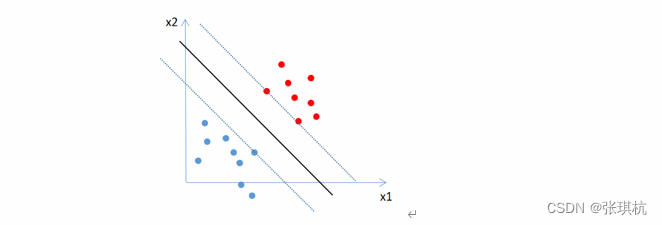
对两类样本点进行分类,如下图,有a线、b线、c线三条线都可以将两类样本点很好的分开类,凭直觉就知道b线是最好的,那是为什么呢?根据概念,要求线到两个类别最近样本点的距离要最大。
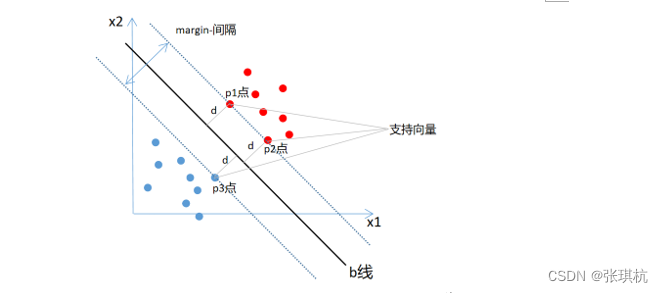
b线就是我们根据支持向量机要找到的分割线,这条线需要到两个类别最近的样本点最远,图上的距离就是d,由于这条线处于两个类别的中间,所以到两个类别的距离都是d。支持向量机SVM算法就是在寻找一个最优的决策边界(上图中的两条虚线)来确定分类线b,所说的支持向量(support vector)就是距离决策边界最近的点(上图中p1、p2、p3点,只不过边界穿过了这些点)。如果没有这些支持向量点,b线的位置就要改变,所以SVM就是根据这些支持向量点来最大化margin,来找到了最优的分类线(machine,分类器),这也是SVM分类算法名称的由来。
2构建svm目标函数
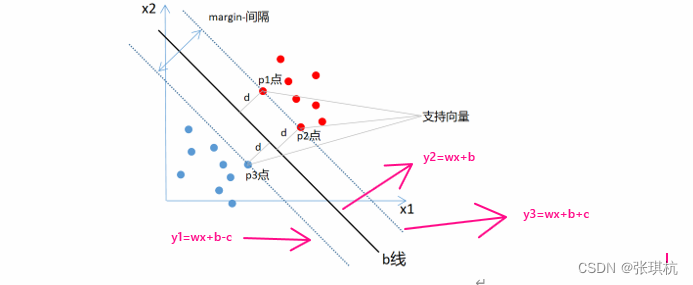
以上面的二分类问题,假设支持向量机最终要找的线是l2,决策边界两条线是l1和l3,那么假设l2的方程为y2=wx+b,要确定l2直线,只需要确定w和b即可,此外,由于l1和l3是l2的决策分类边界线,一定与l2平行的,平行的意味着斜率不变,b改变。而且l2到l1和l3的距离是一样的所以l1和l3的方程可以写成:y1=wx+b-d,y3=wx+b+d。当然机器学习一般表示为wT⋅x+b=0,wT⋅x+b=-c,wT⋅x+b=c
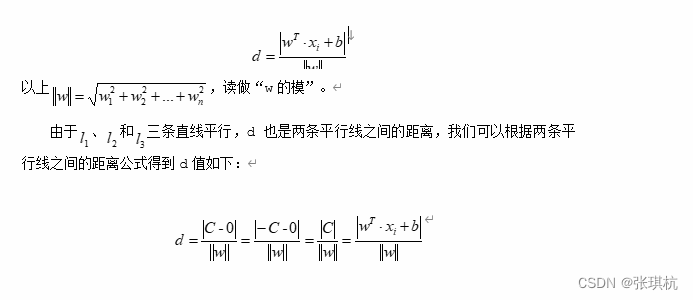
然后根据高中所学的点到点的距离公式,平行线的距离公式就可以推出d
我们希望的是决策边界上的样本点到l2直线的距离d越大越好。我们可以直接计算l1或l3上的点到直线l2的距离。这里是二维的,如果是n维的数据那么点到点的距离公式和平行线的距离公式就为:
我们可以看到无论计算点到直线的距离还是两个平行线之间的距离,最终结果都是d。对于l1直线y=wx+b-d我们可以两边同时除以d结果不变,y/d=wx/d+b-1,也就是wx/d-y/d+b/d=-1,同理得l2和l3分别可变成wx/d-y/d+b/d=0,wx/d-y/d+b/d=1。带入距离公式:
我们希望决策边界上的点到超平面l2距离d越大越好。我们将l3上方的点分类标记为“1”类别,将l1下方的点分类标记为“-1”类别,那么我们可以得到如下公式:
&wT⋅xi+b≥1y=1①式&wT⋅xi+b≤-1y=-1②式
所以对于所有样本点我们需要在满足y⋅wT⋅xi+b≥1条件下,最大化d=1/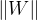
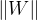
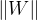
以上n代表样本总数,缩写s.t表示“Subject to”是“服从某某条件”的意思,上述公式描述的是一个典型的不等式约束条件下的二次型函数优化问题,同时也是支持向量机的基本数学模型,这里我们称支持向量机的目标函数。
3.拉格朗日乘法,kkt条件
拉格朗日乘法:
假设x=x1,x2,...,xn是一个n维向量,f(x)和h(x)含有x的函数,我们需要找到满足h(x)=0条件下f(x)最小值,也就是将向量X带入h(x)中结果为0,带入f(x)中结果要最小,我们可以引入一个可以任意取值的自变量
L(x,λ)叫做Lagrange函数(拉格朗日函数),λ叫做拉格朗日乘子(其实就是系数)。令L(x,λ)对x的导数为0,对λ的导数为0,求解出x,λ 的值,那么x就是函数f(x)在附加条件h(x)下极值点。
以上就是拉格朗日乘数法,通俗理解拉格朗日乘数法就是将含有等式条件约束优化问题转换成了无约束优化问题构造出拉格朗日函数L(x,λ),让L(x,λ)对未知数x和λ进行求导,得到一组方程式,可以计算出对应的x和λ结果,这个x对应的f(x)函数值就是在条件h(x)下的最小值点。
kkt条件
其实kkt条件和拉格朗日差不多,差别就在拉格朗日的条件是h(x)=0,而kkt是h(x)<=0,而kkt是解决不等式问题,拉格朗日是解决等式问题,也就是假设x=x1,x2,...,xn是一个n维向量,f(x)和h(x)含有x的函数,我们需要找到满足h(x)≤0条件下f(x)最小值,针对上式,显然是一个不等式约束最优化问题,不能再使用拉格朗日乘数法,因为拉格朗日乘数法是针对等式约束最优化问题。
那我们可以考虑加入一个“松弛变量”a**2让条件h(x)≤0来达到等式的效果,即使条件变成h(x)+a2=0,这里加上a2的原因是保证加的一定是非负数,即:a2≥0,但是目前不知道这个a2值是多少,一定会找到一个合适的a2值使h(x)+a2=0成立。我们就把他变成等式约束了,就可以使用拉格朗日来操作了,只是多了a这个参数
然后分别对三个参数求导
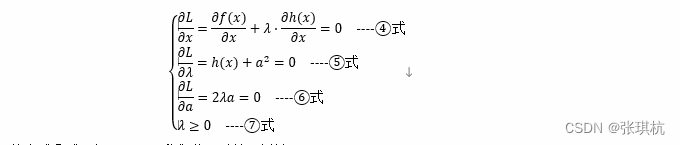
从上式⑥式可知λa=0,我们分两种情况讨论:
- λ=0,a≠0
由于λ=0,根据③式可知,约束不起作用,根据①式可知h(x)≤0。
- λ≠0,a=0
由于λ≠0,根据③式可知λ>0。由于a=0,约束条件起作用,根据⑤式可知,h(x)=0。
综上两个步骤我们可以得到λ⋅h(x)=0,且在约束条件起作用时,λ>0,h(x)=0;约束条件不起作用时,λ=0,h(x)≤0。
上面方程组中的⑥式可以改写成λ⋅h(x)=0。由于a**2≥0,所以将⑤式也可以改写成h(x)≤0,所以上面方程组也可以转换成如下:
以上便是不等式约束优化问题的KKT(Karush-Kuhn-Tucker)条件,我们回到最开始要处理的问题上,根据③式可知,我们需要找到合适的x,λ,a值使L(x,λ,a)最小,但是合适的x,λ,a必须满足KKT条件。
我们对③式的优化问题可以进行优化如下
满足最小化⑧式对应的x,λ值一定也要满足KKT条件,假设现在我们找到了合适的参数x值使f(x)取得最小值P【注意:这里根据①式来说,计算f(x)的最小值,这里假设合适参数x值对应的f(x)的值P就是最小值,不存在比这更小的值。】,由于⑧式中λh(x)一定小于等于零,所以一定有
为了找到最优的λ值,我们一定想要L(x,λ)接近P,即找到合适的λ最大化L(x,λ),可以写成maxλL(x,λ),所以⑧式求解合适的x,λ值最终可以转换成如下
对偶问题
对偶问题是我们定义的一种问题,对于一个不等式约束的原问题(不懂的搜一下)

我们定义对偶问题为(对上面方程的求解等效求解下面方程)
其实就是把min和max对调了一下,当然对应的变量也要变换
对偶问题有什么好处呢?对于原问题,我们要先求里面的max,再求外面的min。而对于对偶问题,我们可以先求里面的min。有时候,先确定里面关于x的函数最小值,比原问题先求解关于λ的最大值,要更加容易解
但是原问题跟对偶问题并不是等价的,这里有一个强对偶性、弱对偶性的概念,弱对偶性是对于所有的对偶问题都有的一个性质,弱对偶:
其中 x*,λ*是函数取最大值最小值的时候对应的最优解,也就是说,原问题始终大于等于对偶问题
如果两个问题是强对偶的,那么这两个问题其实是等价的问题
所有的下凸函数都满足强对偶性,也就是说所有下凸函数都满足上式
4.最小化SVM目标函数
通过1.2小节我们知道SVM目标函数如下,s.t表示在什么条件之下
根据拉格朗日乘数法、KKT条件、对偶问题我们可以按照如下步骤来计算SVM目标函数最优的一组w值
kkt条件:
因为上式子的条件是不等式约束,那么就的用kkt条件
根据kkt条件推出的的式子9带入SVM目标函数得:
以上不等式转换成拉格朗日函数必须满足KKT条件,详见KKT条件,这里满足的KKT条件如下
计算分割线w和b的值:
对偶转换:
由于原始目标函数是个下凸函数,根据1.3.3中对偶问题可知L(w,b,λ)一定是强对偶问题,所以可以将a式改写成如下
针对b式,我们假设参数λ固定,使L(w,b,λ)对参数w和b进行求导得到如下
进一步可以得到
按照解方程组的思想,我们现在将以上计算得到的结果代入到b式中得到
我们可以发现以上公式经过转换只含有λ的方程求极值问题,但是λ
含有λi,λj…这些未知数(注意不是2个),那么我们要求的一组w如何得到呢?只要针对以上公式得到λ
值后,我们可以根据c式进一步求解到对应的一组w值。针对上式求极值问题,我们常用 SMO(Sequential Minimal Optimization) 算法求解λi,λj…。
注意:d式中(xi⋅xj)代表两个向量的点积,也叫内积,例如:xi=(xi1,xi2),xj=(xj1,xj2)那么两个向量点积结果为xi1⋅xj1+xi2⋅xj2
当λ>0时,一定有1-yi⋅wT⋅xi+b=0,对于这样的样本就属于支持向量点,就在分类边界上,我们将对应的w代入到yi⋅wT⋅xi+b=1中,然后两边乘yi,得到yi**2⋅wT⋅xi+b=yi。由于yi**2=1,所以:
假设我们有S个支持向量,以上b的计算可以使用任意一个支持向量代入计算即可,如果数据严格是线性可分的,这些b结果是一致的对于数据不是严格线性可分的情况,参照后面的软间隔问题,一般我们可以采用一种更健壮的方式,将所有支持向量对应的b都求出,然后将其平均值作为最后的结果,最终b的结果如下
5软间隔及优化
以上讨论问题都是基于样本点完全的线性可分,我们称为硬间隔如下图
如果存在部分样本点不能完全线性可分,大部分样本点线性可分的情况,如下图所示
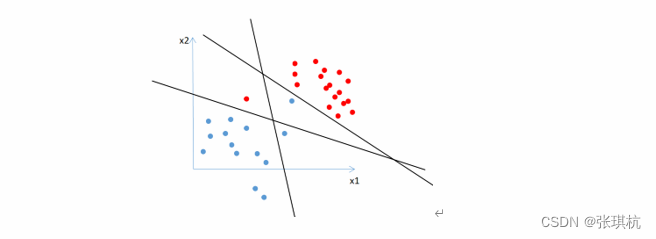
那么我们就需要用到软间隔,相比于硬间隔的苛刻条件,我们允许个别样本点出现在间隔带里面
即我们允许部分样本点不满足约束条件y⋅wT⋅xi+b≥1
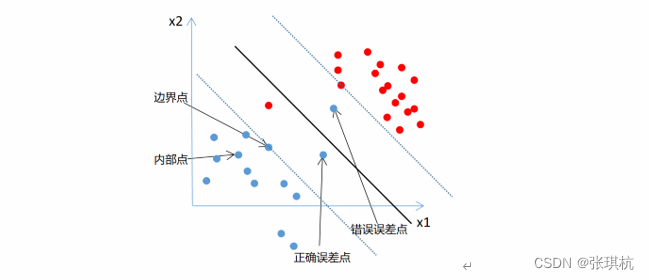
为了度量这个间隔软到何种程度,我们为每个样本引入一个“松弛变量”ξi,ξi≥0,(中文:克西)加入松弛变量后,我们的约束条件变成y⋅wT⋅xi+b≥1-ξi,这样不等式就不会那么严格,数据点在不同的约束条件下的情况如下
- 内部点:y⋅wT⋅xi+b>1,即ξi=0
- 边界点:y⋅wT⋅xi+b=1,即ξi=0
- 正确误差点:y⋅wT⋅xi+b=1-ξi,即0<ξi<1
- 错误误差点:y⋅wT⋅xi+b=1-ξi,即ξi≥1
优化svm目标函数
加入软间隔后我们的目标函数变成了
其中C是一个大于0的常数,这里在原有的目标函数中加入Ci=1nξi可以理解为错误样本的惩罚程度,我们希望在对应条件下min12w2+Ci=1nξi变小,对应的也是希望Ci=1nξi变小,当C为无穷大,ξi必然无穷小,这样的话SVM就变成一个完全线性可分的SVM。如果C为有对应的值时,ξi对应的会有一个大于0的值,这样的SVM就是允许部分样本不遵守约束条件。
接下来我们对新的目标函数h式求解最优化问题,步骤与1.4 SVM“硬间隔”完全线性可分步骤完全一
构造拉格朗日函数
将h式目标函数改写成如下
构造拉格朗日函数如下
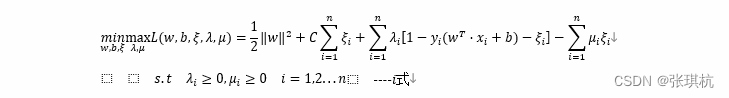
上式中λi,μi是拉格朗日乘子,w,b,ξ是我们要计算的主问题参数
对偶转换关系:
目标函数是个下凸函数,对应的拉格朗日函数复合强对偶性,所以可以根据强对偶向,将对偶问题转换为
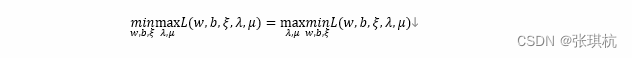


我们发现上式中求与μ
没有关系,但是为什么可以消掉是因为
,所以在约束条件中一定有此条件,所以我们得到最终的目标函数可以写成如下
推导到以上之后,我们发现结果和硬间隔结果一样,参照1.4.3 d式,只是结果中多了约束条件C=λi+μi
求解结果:
同样我们也可以利用SMO算法对式L求解得到一组合适的λ值和μ值,由于综上所述,我们可以的到最终的w和b的值如下
这里得到的w和b虽然和硬分割结果一样,但是这是加入松弛变量之后得到的w和b的值,根据L式的条件C=λi+μi和λi≥0,μi≥0,结合h式,C越大,必然导致松弛越小,如果C无穷大,那么就意味着模型过拟合,在训练SVM时,C是我们需要调节的参数。
那么确定w和b之后,我们就能构造出最大分割超平面:wT⋅x+b=0,新来样本对应的特征代入后得到的结果如果是大于0那么属于一类,小于0属于另一类
总结:
SVM向量机就是使用拉格朗日,kkt条件,对偶问题来求的线或超平面的参数W和b,从而对目标进行分类的一个算法