正文
一.概述
1.本次数据结构所做5个题目:
11.2.1一元稀疏多项式计算器
11.2.5模拟浏览器操作系统
11.2.10图的基本操作与实现
11.2.18八皇后问题
11.2.21木棒加工问题
2.使用语言:
C语言
3.编译环境:
Dev-C++;Microsoft Visual C++ 6.0
二.课程设计题目
1.一元稀疏多项式计算器
1.1问题描述
设计一个一元稀疏多项式简单计算器。
1.2需求分析
- 输入并建立多项式。
- 输出多项式,输出形式为整数序列:n.c1.e1,c2,e2,....cn,en,其中 n是多项式的项数,ci,ei,分别是第i项的系数和指数,序列按指数降序排序。
(4)实现多项式 a和 b 相加,建立多项式 a+b。
(5)实现多项式 a和 b相减,建立多项式 a—b。
(6)计算多项式在×处的值。
(7)计算器的仿真界面
1.3算法的设计与实现
1.3.1设计思路
1. 输入并建立多项式:
- 用户输入多项式的项数n。
- 循环n次,每次输入一个项的系数ci和指数ei。
- 将所有输入的项保存在一个列表中。
2. 输出多项式:
- 对保存的多项式进行按指数降序排序。
- 遍历排序后的多项式列表,依次输出每个项的系数和指数。
3. 多项式相加:
- 用户输入两个多项式a和b。
- 创建一个空的结果多项式c。
- 遍历a和b的项,将对应指数相同的项的系数相加,并将结果添加到c中。
- 如果某个多项式的项已经遍历完,将另一个多项式剩余的项直接添加到c中。
4. 多项式相减:
- 用户输入两个多项式a和b。
- 创建一个空的结果多项式c。
- 遍历a和b的项,将对应指数相同的项的系数相减,并将结果添加到c中。
- 如果某个多项式的项已经遍历完,将另一个多项式剩余的项取相反数后直接添加到c中。
5. 计算多项式在×处的值:
- 用户输入一个值x。
- 遍历多项式的每个项,将每个项的系数乘以x的指数次幂,并累加得到结果。
6. 计算器的仿真界面:
- 可以使用图形用户界面(GUI)库来实现计算器的界面。
- 在界面上提供输入框和按钮,用于输入多项式、操作符和值。
- 根据用户的选择,调用相应的函数进行计算,并在界面上显示结果。
1.3.2主要函数说明与源程序代码
主要函数:
dnode *creat() //用链表存放多项式
void swap(dnode *p,dnode *q) /*交换p,q指针所指的指数和系数*/
void sort(dnode *h) /*采用冒泡法对链表每一项重新排序*/
dnode *operate(dnode *a,dnode *b) /*稀疏多项式计算*/
void prn(dnode *h)//打印结果
float qiuzhi(int x,dnode *h) //求多项式在x处的值
源代码:
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>
#define NULL 0
typedef struct node /*定义多项式每一项*/
{
int e; //e为指数
float c; //c为系数
struct node *next; //next指向下一项
}dnode;
dnode *creat() /*用链表存放多项式*/
{ //多项式的创建, 即输入两个多项式
dnode *h,*p;
int e,i,n; //n为多项式的项数
float c; //c为多项式的系数
h=(dnode *)malloc(sizeof(dnode)); //分配头节点
h->next=NULL;
do //当n为0或小于1时,则重新输入
{
printf("请输入多项式的项数n:");
scanf("%d",&n);
}while(n<1);
for(i=1;i<=n;i++) //输入各项的系数c和指数e
{
printf("请输入第%d项的系数c和指数e:",i);
scanf("%f%d",&c,&e);
p=(dnode *)malloc(sizeof(dnode)); //创建新结点
p->c=c;p->e=e; //将值传给data域
p->next=h->next;//用头插法建立链表
h->next=p;
}
return h; //返回头结点
}
void swap(dnode *p,dnode *q) /*交换p,q指针所指的指数和系数*/
{
float m; //中间变量
int n; //中间变量
n=p->e; //交换操作
p->e=q->e;
q->e=n;
m=p->c;
p->c=q->c;
q->c=m;
}
void sort(dnode *h) /*采用冒泡法对链表每一项重新排序*/
{
dnode *pi,*pl,*p,*q;
p=h->next; //p此时指向第一项
while(p->next!=NULL)
p=p->next; //寻找尾结点
pi=p; //pi指向最后一次交换的位置,初值为表尾
while(pi!=h->next) //结点数大于1时
{
pl=h->next; //为中间变量,起传递地地址的作用
for(p=h->next;p!=pi;p=p->next)
{
q=p->next;
if(p->e>q->e)
{
swap(p,q); //调用交换函数
pl=p;
}
}
pi=pl; //pi指向前一个结点
}
}
dnode *operate(dnode *a,dnode *b) /*稀疏多项式计算*/
{
int sel;
float x;
dnode *p1,*p2,*p,*t; //t为结果链表的表头
t=(dnode *)malloc(sizeof(dnode));
t->next=NULL;
printf("--------------------------------------\n");
printf("| 请选择运算方式: |\n");
printf("| 1、多项式相加 |\n");
printf("| 2、多项式相减 |\n");
printf("| 0、退出! |\n");
printf("--------------------------------------\n");
printf("请选择:");
scanf("%d",&sel);
p1=a->next;
p2=b->next;
while(p1&&p2)
{
if(p1->e==p2->e) //指数相同
{
if(sel==1)
x=p1->c+p2->c; //系数相加
else
x=p1->c-p2->c; //系数相减
if(x!=0)
{
p=(dnode *)malloc(sizeof(dnode));
p->e=p1->e;
p->c=x;
p->next=t->next;//利用头插法将p结点插入t中
t->next=p;
}
p1=p1->next;
p2=p2->next;
}
else if(p1->e>p2->e) //p1的指数大于p2的指数
{
p=(dnode *)malloc(sizeof(dnode));
p->e=p2->e;
if(sel==1)
p->c=p2->c;
else
p->c=(-1)*p2->c;
p->next=t->next;
t->next=p;
p2=p2->next;
}
else //p1的指数小于p2的指数
{
p=(dnode *)malloc(sizeof(dnode));
p->e=p1->e;
p->c=p1->c;
p->next=t->next;
t->next=p;
p1=p1->next;
}
}
while(p1!=NULL) //p2为空,p1不为空时
{
p=(dnode *)malloc(sizeof(dnode));
p=p1;
p1=p1->next;
p->next=t->next; //把p1 放在结果链表后面
t->next=p;
}
while(p2!=NULL) //p1为空,p2不为空时
{
p=(dnode *)malloc(sizeof(dnode));
p->e=p2->e;
if(sel==2) //如果选择的是2,则将p2中剩余的项的系数取其相反数
p->c=(-1)*p2->c;
else
p->c=p2->c;
p2=p2->next;
p->next=t->next; //把p1 放在结果链表后面
t->next=p;
}
return t; //返回运算后的多项式的头结点
}
void prn(dnode *h)//打印结果
{
dnode *p;
p=h->next;
if(p==NULL) //如果多项式项数为0
{
printf("多项式项数为0,退出!\n");
exit(0);
}
printf("生成的多项式如下:\n");
while((p->next)!=NULL) //否则,则输出
{
printf("%3.1f X^%d + ",p->c,p->e);
p=p->next;
}
if(p->next==NULL)
{
printf("%3.1f X^%d\n",p->c,p->e);
}
}
float qiuzhi(int x,dnode *h) //求多项式在x处的值
{
dnode *p;
float sum=0;
int i,t;
printf("请输入x的值:");
scanf("%d",&x);
for(p=h->next;p;p=p->next)
{
t=1;
for(i=p->e;i!=0;)
{
if(i<0){t/=x;i++;}//指数小于0,进行除法
else{t*=x;i--;} //指数小于0,进行除法
}
sum+=p->c*t;
}
return sum;
}
void main()
{
int x;
float sum=0;
dnode *a,*b,*c;
a=creat(); //第一个多项式
sort(a); //排序
prn(a); //打印结果
b=creat(); //第二个多项式
sort(b); //排序
prn(b); //打印结果
c=operate(a,b); //结果多项式
prn(c); //打印
sum=qiuzhi(x,c);
printf("多项式的值为:%.3f",sum);
printf("\n");
}1.4 调试分析与测试结果
1.4.1.调试:
【问题一】
- 输入错误:用户输入的多项式格式不正确,例如指数为负数或非整数,系数为非数字等。
【问题二】
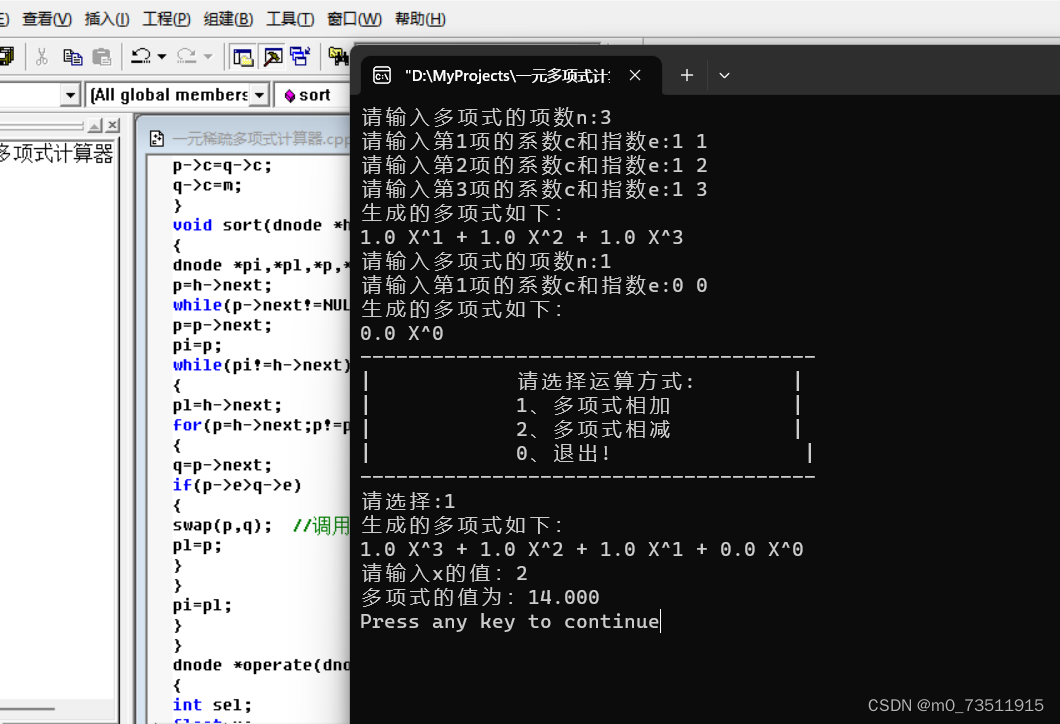
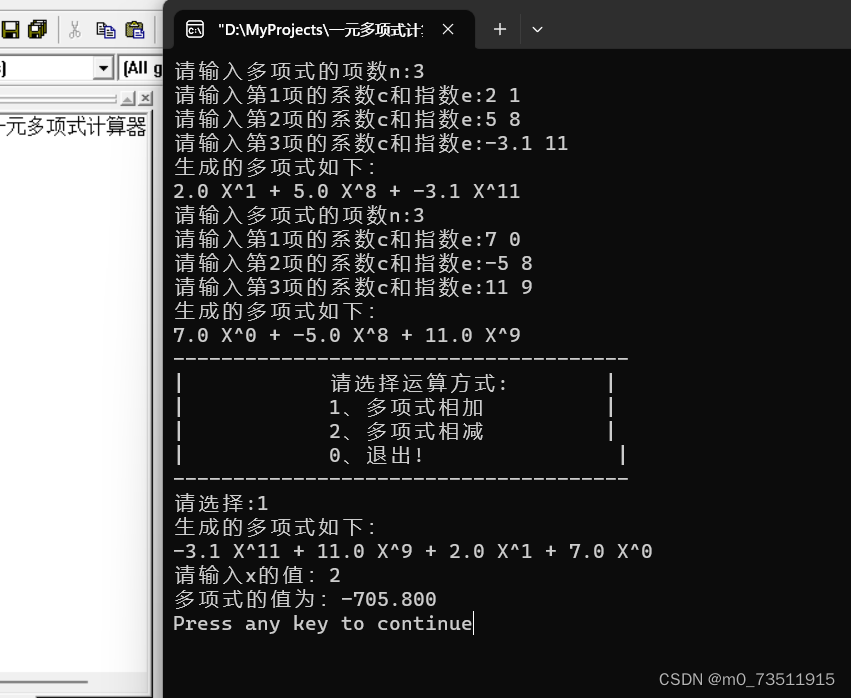
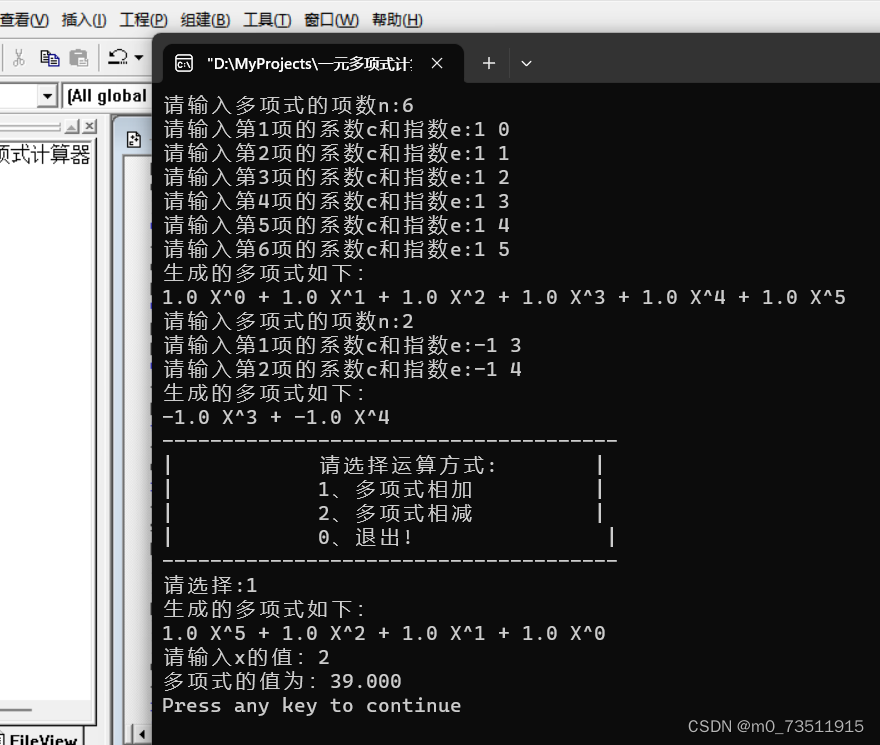
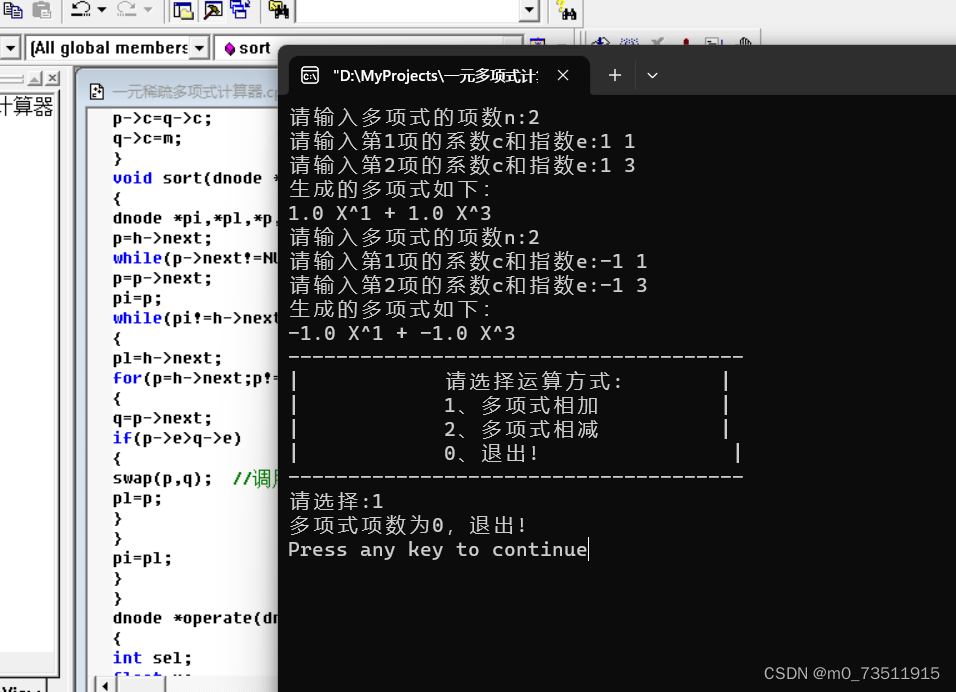
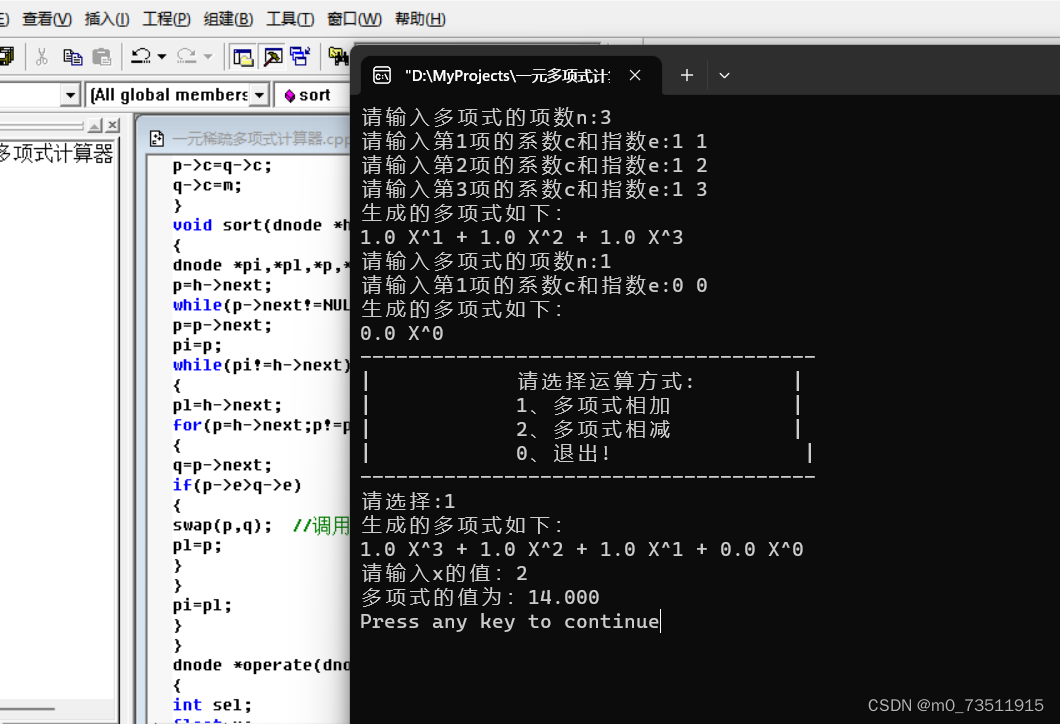
1.4.2测试结果:
2.模拟浏览器操作程序
2.1问题描述
标准Web浏览器具有在最近访问的网页间后退和前进的功能。实现这些功能的一个方法是:使用两个栈,追踪可以后退和前进而能够到达的网页。在本题中,要求模拟实现这一功能。
2.2需求分析
需要支持以下指令:
BACK:将当前页推到“前进栈”的顶部。取出“后退栈”中顶端的页面,使它成为当前页。若“后退栈”是空的,忽略该命令。
FORWARD:将当前页推到“后退栈”的顶部。取出“前进栈”中顶部的页面,使它成为当前页。如果“前进栈”是空的,忽略该命令。
VISIT <url>:将当前页推到“后退栈”的顶部。使 URL特指当前页。清空“前进栈”。
QUIT:退出浏览器。
假设浏览器首先加载的网页 URL 是:
2.3算法的设计与实现
2.3.1设计思路
运用了栈,“先进后出,后进先出”的特点。BACK,FORWARD操作对应的进行栈的进出。此外,还设置了标志位flag判断是否退出,将num与栈的长度进行比较,确定输出网址还是ignore。
2.3.2主要函数说明
void PUSHQ(QU *qu, char cur[ ])//入队
void POPQ(QU *qu)//出队
void PUSH(ST *st, char cur[])//入栈
void POP(ST *st)//出栈
void BACK(ST *stfront,ST *strear,char cur[], QU *qu)//回溯
void FORWARD(ST *stfront, ST *strear, char cur[], QU *qu)//前寻
void VISIT(ST *stfront,ST *strear, char cur[],QU *qu)//访问
【源程序】
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct stack
{
char s[100][70];
int top;
}ST;//栈定义
typedef struct queue
{
char q[100][70];
int head;
int tail;
}QU;//队列定义,用于接受输出
void PUSHQ(QU *qu, char cur[])//入队
{
if (qu->tail == 100)
{
printf("队满\n");
}
else
{
qu->tail++;
strncpy(qu->q[qu->tail], cur,strlen(cur) + 1);
}
}
void POPQ(QU *qu)//出队
{
qu->head++;
}
void PUSH(ST *st, char cur[])//入栈
{
if (st->top == 100)
{
printf("栈满\n");
}
else
{
strncpy(st->s[st->top],cur,strlen(cur)+1);
st->top++;
}
}
void POP(ST *st)//出栈
{
if (st->top == 0)
{
printf("栈空\n");
}
else
{
st->top--;
}
}
int EMPTY(ST *st)//判空
{
if (st->top == 0)
return 1;
else
return 0;
}
void BACK(ST *stfront,ST *strear,char cur[], QU *qu)//回溯
{
if (!EMPTY(strear))
{
PUSH(stfront, cur);
POP(strear);
strncpy(cur,strear->s[strear->top],strlen(strear->s[strear->top]) + 1);
PUSHQ(qu, cur);
}
else
{
char *a = "Ignored";
PUSHQ(qu, a);
}
}
void FORWARD(ST *stfront, ST *strear, char cur[], QU *qu)//前寻
{
if (!EMPTY(stfront))
{
PUSH(strear, cur);
POP(stfront);
strncpy(cur, stfront->s[stfront->top],strlen(stfront->s[stfront->top]) + 1);
PUSHQ(qu, cur);
}
else
{
char *a = "Ignored";
PUSHQ(qu,a);
}
}
void VISIT(ST *stfront,ST *strear, char cur[],QU *qu)//访问
{
PUSHQ(qu, cur);
stfront->top = 0;
}
int main()
{
printf("输入:\n");
ST stfront;
ST strear;
stfront.top = 0;
strear.top = 0;
QU qu;
qu.head = -1;
qu.tail = -1;
char cur[70];
char start[70] = "http://www.acm.org/";//需先对此网站进行如回溯栈的特殊处理
char in[2][70];
strncpy(cur, start,strlen(start) + 1);
scanf("%s", in[0], 70);
while (strcmp(in[0], "QUIT") != 0)
{
if (strcmp(in[0], "VISIT") == 0)
{
PUSH(&strear, cur);
scanf("%s", in[1], 70);
strncpy(cur,in[1],strlen(in[1])+1);
VISIT(&stfront, &strear, cur, &qu);
}
else if (strcmp(in[0], "QUIT") == 0)
{
break;
}
else if (strcmp(in[0], "BACK") == 0)
{
BACK(&stfront, &strear, cur, &qu);
}
else
{
FORWARD(&stfront, &strear, cur, &qu);
}
scanf("%s", in[0], 70);
}
printf("输出:\n");//输出
while (qu.head != qu.tail)
{
POPQ(&qu);
printf("%s\n", qu.q[qu.head]);
}
return 0;
}2.4调试分析与结果测试
2.4.1调试分析:
后退栈为空时执行BACK指令:
- 当用户执行BACK指令时,程序应检查后退栈是否为空。
- 如果后退栈为空,则无法执行BACK指令,程序应忽略该命令。
- 当用户执行FORWARD指令时,程序应检查前进栈是否为空。
- 如果前进栈为空,则无法执行FORWARD指令,程序应忽略该命令。
执行VISIT指令:
- 当用户执行VISIT指令时,程序应将当前页推到后退栈的顶部。
- 如果指定的URL与当前页相同,则不进行任何操作。
- 程序应清空前进栈,以确保用户在执行其他操作时无法前进到已访问的页面。
执行QUIT指令:
- 当用户执行QUIT指令时,程序应退出浏览器。
初始加载网页URL:
- 浏览器首次加载网页URL为http://www.acm.org/。
- 程序应将此URL作为当前页,并将其推入后退栈的顶部。
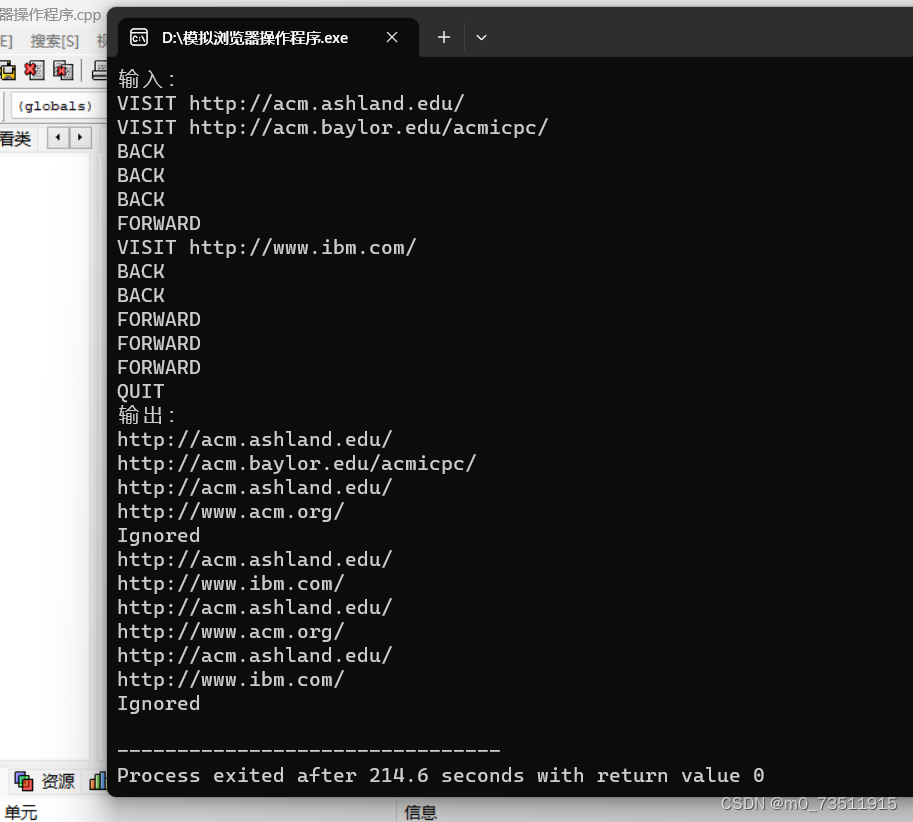
2.4.2测试结果
3.图的基本操作与实现
3.1问题描述
要求用邻接表存储结构,实现对图 11-3 所示的有向带权网络 G 的操作。
3.2需求分析
(1)输入含 n(1≤n≤100)个顶点(用字符表示顶点)和e条边。
(2)求每个顶点的出度和人度,输出结果。
(3)指定任意顶点×为初始顶点,对图G作DFS遍历,输出 DFS 顶点序列。
(4)指定任意顶点x为初始顶点,对图G作BFS 遍历,输出 BFS 顶点序列。
(5)输入顶点 x,查找图 G:若存在含x 的顶点,则删除该结点及与之相关联的边,并作 DFS遍历;否则输出信息“无x”。
(6)判断图 G是否是连通图,输出信息“YES”/“NO”。
(7)根据图 G 的邻接表创建图 G 的邻接矩阵,即复制图G。
(8)找出该图的一棵最小生成树。
3.3算法设计与实现
3.3.1设计思路
1. 创建一个图的类,包含顶点和边的数据结构和操作方法。
2. 定义一个函数,接受输入的顶点和边的数量,并创建对应数量的顶点和边。
3. 定义函数来计算每个顶点的出度和入度,并输出结果。
4. 定义DFS遍历函数,接受初始顶点作为参数,使用递归或者栈来实现深度优先搜索,并输出DFS顶点序列。
5. 定义BFS遍历函数,接受初始顶点作为参数,使用队列来实现广度优先搜索,并输出BFS顶点序列。
6. 定义函数来接受输入的顶点x,并查找图G中与之相关联的顶点和边。如果存在顶点x,则删除该顶点及与之相关联的边,并进行DFS遍历;否则输出"无x"。
7. 定义函数来判断图G是否是连通图。使用DFS或BFS遍历,检查是否可以遍历到所有的顶点。如果可以,则输出"YES";否则输出"NO"。
8. 定义函数来根据图G的邻接表创建邻接矩阵,并复制图G。
9. 定义函数来找出图的一棵最小生成树。使用Prim算法或Kruskal算法来实现。
3.3.2主要函数说明及源程序
//有向带权图,邻接表中的节点
typedef struct Node {
int value;//顶点下标,也可以说是值
int weight;//权
struct Node* next;//指针域
} Node;
// 图的结构
typedef struct Graph {
int numNodes;//节点数
Node** adjacencyList;
} Graph;
// 创建节点
Node* createNode(int value, int weight) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->value = value;
newNode->weight = weight;
newNode->next = NULL;
return newNode;
}
// 创建图,传入节点数
Graph* createGraph(int numNodes) {
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->numNodes = numNodes;
graph->adjacencyList = (Node**)malloc(numNodes * sizeof(Node*));
// 初始化邻接表为空
for (int i = 0; i < numNodes; i++) {
graph->adjacencyList[i] = NULL;
}
return graph;
}
// 添加边
void addEdge(Graph* graph, int source, int target, int weight) {
// 创建新的节点
Node* newNode = createNode(target, weight);
// 将新节点插入到源节点的邻接表中,顶点以下标为标准直接以头插法插入
newNode->next = graph->adjacencyList[source];
graph->adjacencyList[source] = newNode;
}
// 求顶点的出度
int outDegree(Graph* graph, int vertex) {
Node* currentNode = graph->adjacencyList[vertex];
int outDegree = 0;
while (currentNode != NULL) {
outDegree++;
currentNode = currentNode->next;
}
return outDegree;
}
// 求顶点的入度,遍历整个邻接表
int inDegree(Graph* graph, int vertex) {
int inDegree = 0;
for (int i = 0; i < graph->numNodes; i++) {
Node* currentNode = graph->adjacencyList[i];
while (currentNode != NULL) {
if (currentNode->value == vertex) {
inDegree++;
}
currentNode = currentNode->next;
}
}
return inDegree;
}
// 深度优先,递归遍历
void DFS(Graph* graph, int vertex, int* visited) {
visited[vertex] = 1;
printf("%d ", vertex);
Node* currentNode = graph->adjacencyList[vertex];
while (currentNode != NULL) {
int neighbor = currentNode->value;
if (!visited[neighbor]) {
DFS(graph, neighbor, visited);
}//如果此顶点未被访问,则继续深度优先遍历
currentNode = currentNode->next;
}
}
// 广度优先遍历
void BFS(Graph* graph, int startVertex) {
int* visited = (int*)malloc(graph->numNodes * sizeof(int));
for (int i = 0; i < graph->numNodes; i++) {
visited[i] = 0;
}
// 创建队列
int* queue = (int*)malloc(graph->numNodes * sizeof(int));
int front = 0;
int rear = 0;
visited[startVertex] = 1;
printf("%d ", startVertex);
queue[rear++] = startVertex;
while (front < rear) {
int vertex = queue[front++];
Node* currentNode = graph->adjacencyList[vertex];
while (currentNode != NULL) {
int neighbor = currentNode->value;
if (!visited[neighbor]) {
visited[neighbor] = 1;
printf("%d ", neighbor);
queue[rear++] = neighbor;
}
currentNode = currentNode->next;
}
}
free(visited);
free(queue);
}
// 查找顶点
bool searchVertex(Graph* graph, int vertex) {
for (int i = 0; i < graph->numNodes; i++) {
Node* currentNode = graph->adjacencyList[i];
while (currentNode != NULL) {
if (currentNode->value == vertex) {
return true;
}
currentNode = currentNode->next;
}
}
return false;
}
// 判断是否为连通图
bool isConnected(Graph* graph) {
int* visited = (int*)malloc(graph->numNodes * sizeof(int));
for (int i = 0; i < graph->numNodes; i++) {
visited[i] = 0;
}
DFS(graph, 0, visited);
for (int i = 0; i < graph->numNodes; i++) {
if (visited[i] == 0) {
free(visited);
return false;
}
}
free(visited);
return true;
}
// 创建邻接矩阵
int** createAdjacencyMatrix(Graph* graph) {
int** matrix = (int**)malloc(graph->numNodes * sizeof(int*));
for (int i = 0; i < graph->numNodes; i++) {
matrix[i] = (int*)malloc(graph->numNodes * sizeof(int));
for (int j = 0; j < graph->numNodes; j++) {
matrix[i][j] = 0;
}
}
for (int i = 0; i < graph->numNodes; i++) {
Node* currentNode = graph->adjacencyList[i];
while (currentNode != NULL) {
matrix[i][currentNode->value] = currentNode->weight;
currentNode = currentNode->next;
}
}
return matrix;
}
【源程序】
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
//有向带权图
// 邻接表中的节点
typedef struct Node {
int value;//顶点下标,也可以说是值
int weight;//权
struct Node* next;//指针域
} Node;
// 图的结构
typedef struct Graph {
int numNodes;//节点数
Node** adjacencyList;
} Graph;
// 创建节点
Node* createNode(int value, int weight) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->value = value;
newNode->weight = weight;
newNode->next = NULL;
return newNode;
}
// 创建图,传入节点数
Graph* createGraph(int numNodes) {
Graph* graph = (Graph*)malloc(sizeof(Graph));
graph->numNodes = numNodes;
graph->adjacencyList = (Node**)malloc(numNodes * sizeof(Node*));
// 初始化邻接表为空
for (int i = 0; i < numNodes; i++) {
graph->adjacencyList[i] = NULL;
}
return graph;
}
// 添加边
void addEdge(Graph* graph, int source, int target, int weight) {
// 创建新的节点
Node* newNode = createNode(target, weight);
// 将新节点插入到源节点的邻接表中,顶点以下标为标准直接以头插法插入
newNode->next = graph->adjacencyList[source];
graph->adjacencyList[source] = newNode;
}
// 求顶点的出度
int outDegree(Graph* graph, int vertex) {
Node* currentNode = graph->adjacencyList[vertex];
int outDegree = 0;
while (currentNode != NULL) {
outDegree++;
currentNode = currentNode->next;
}
return outDegree;
}
// 求顶点的入度,遍历整个邻接表
int inDegree(Graph* graph, int vertex) {
int inDegree = 0;
for (int i = 0; i < graph->numNodes; i++) {
Node* currentNode = graph->adjacencyList[i];
while (currentNode != NULL) {
if (currentNode->value == vertex) {
inDegree++;
}
currentNode = currentNode->next;
}
}
return inDegree;
}
// 深度优先,递归遍历
void DFS(Graph* graph, int vertex, int* visited) {
visited[vertex] = 1;
printf("%d ", vertex);
Node* currentNode = graph->adjacencyList[vertex];
while (currentNode != NULL) {
int neighbor = currentNode->value;
if (!visited[neighbor]) {
DFS(graph, neighbor, visited);
}//如果此顶点未被访问,则继续深度优先遍历
currentNode = currentNode->next;
}
}
// 广度优先遍历
void BFS(Graph* graph, int startVertex) {
int* visited = (int*)malloc(graph->numNodes * sizeof(int));
for (int i = 0; i < graph->numNodes; i++) {
visited[i] = 0;
}
// 创建队列
int* queue = (int*)malloc(graph->numNodes * sizeof(int));
int front = 0;
int rear = 0;
visited[startVertex] = 1;
printf("%d ", startVertex);
queue[rear++] = startVertex;
while (front < rear) {
int vertex = queue[front++];
Node* currentNode = graph->adjacencyList[vertex];
while (currentNode != NULL) {
int neighbor = currentNode->value;
if (!visited[neighbor]) {
visited[neighbor] = 1;
printf("%d ", neighbor);
queue[rear++] = neighbor;
}
currentNode = currentNode->next;
}
}
free(visited);
free(queue);
}
// 查找顶点
bool searchVertex(Graph* graph, int vertex) {
for (int i = 0; i < graph->numNodes; i++) {
Node* currentNode = graph->adjacencyList[i];
while (currentNode != NULL) {
if (currentNode->value == vertex) {
return true;
}
currentNode = currentNode->next;
}
}
return false;
}
// 判断是否为连通图
bool isConnected(Graph* graph) {
int* visited = (int*)malloc(graph->numNodes * sizeof(int));
for (int i = 0; i < graph->numNodes; i++) {
visited[i] = 0;
}
DFS(graph, 0, visited);
for (int i = 0; i < graph->numNodes; i++) {
if (visited[i] == 0) {
free(visited);
return false;
}
}
free(visited);
return true;
}
// 创建邻接矩阵
int** createAdjacencyMatrix(Graph* graph) {
int** matrix = (int**)malloc(graph->numNodes * sizeof(int*));
for (int i = 0; i < graph->numNodes; i++) {
matrix[i] = (int*)malloc(graph->numNodes * sizeof(int));
for (int j = 0; j < graph->numNodes; j++) {
matrix[i][j] = 0;
}
}
for (int i = 0; i < graph->numNodes; i++) {
Node* currentNode = graph->adjacencyList[i];
while (currentNode != NULL) {
matrix[i][currentNode->value] = currentNode->weight;
currentNode = currentNode->next;
}
}
return matrix;
}
int main() {
int numNodes = 6;
Graph* graph = createGraph(numNodes);
addEdge(graph, 0, 1, 2);
addEdge(graph, 0, 2, 3);
addEdge(graph, 1, 2, 1);
addEdge(graph, 2, 3, 4);
addEdge(graph, 3, 1, 5);
addEdge(graph, 3, 4, 2);
addEdge(graph, 4, 0, 1);
addEdge(graph, 4, 2, 3);
addEdge(graph, 5, 3, 2);
// 求每个顶点的出度和入度
for (int i = 0; i < numNodes; i++) {
printf("顶点%d的出度:%d\n", i, outDegree(graph, i));
printf("顶点%d的入度:%d\n", i, inDegree(graph, i));
}
printf("从顶点0开始的DFS顶点序列:");
int* visitedDFS = (int*)malloc(numNodes * sizeof(int));
for (int i = 0; i < numNodes; i++) {
visitedDFS[i] = 0;//生成所有顶点
}
DFS(graph, 0, visitedDFS);
printf("\n");
printf("从顶点0开始的BFS顶点序列:");
BFS(graph, 0);
printf("\n");
int searchVertexValue = 2;
printf("查找顶点%d:", searchVertexValue);
if (searchVertex(graph, searchVertexValue)) {
printf("存在\n");
}
else {
printf("不存在\n");
}
printf("图是否为连通图:");
if (isConnected(graph)) {
printf("是\n");
}
else {
printf("不是\n");
}
int** adjacencyMatrix = createAdjacencyMatrix(graph);
printf("邻接矩阵:\n");
for (int i = 0; i < numNodes; i++) {
for (int j = 0; j < numNodes; j++) {
printf("%d ", adjacencyMatrix[i][j]);
}
printf("\n");
}
} 3.4调试分析与结果测试
3.4.1调试分析:
【问题一】
输入格式错误问题:用户输入的顶点和边的数量可能不符合要求。
解决方法是在接收输入时进行验证,确保顶点和边的数量在有效范围内。
【问题二】
DFS遍历问题:DFS遍历可能陷入无限循环,或者无法访问到所有的顶点。
解决方法是使用一个标记数组来记录已经访问过的顶点,避免重复访问,并确保能够访问到所有的顶点。
【问题三】
BFS遍历问题:BFS遍历可能无法处理有向图中的环路,导致陷入无限循环。
解决方法是使用一个队列来保存待访问的顶点,并使用一个标记数组来记录已经访问过的顶点。
【问题四】
图中不存在指定顶点问题:在进行删除操作或查找操作时,如果图中不存在指定的顶点,可能会引发错误。解决方法是在操作之前进行判断,如果顶点不存在,则输出相应的提示信息。
【问题五】
连通图判断问题:判断图是否为连通图可能需要进行图的遍历。
解决方法是通过DFS或BFS遍历图,并检查是否能够访问到所有的顶点。
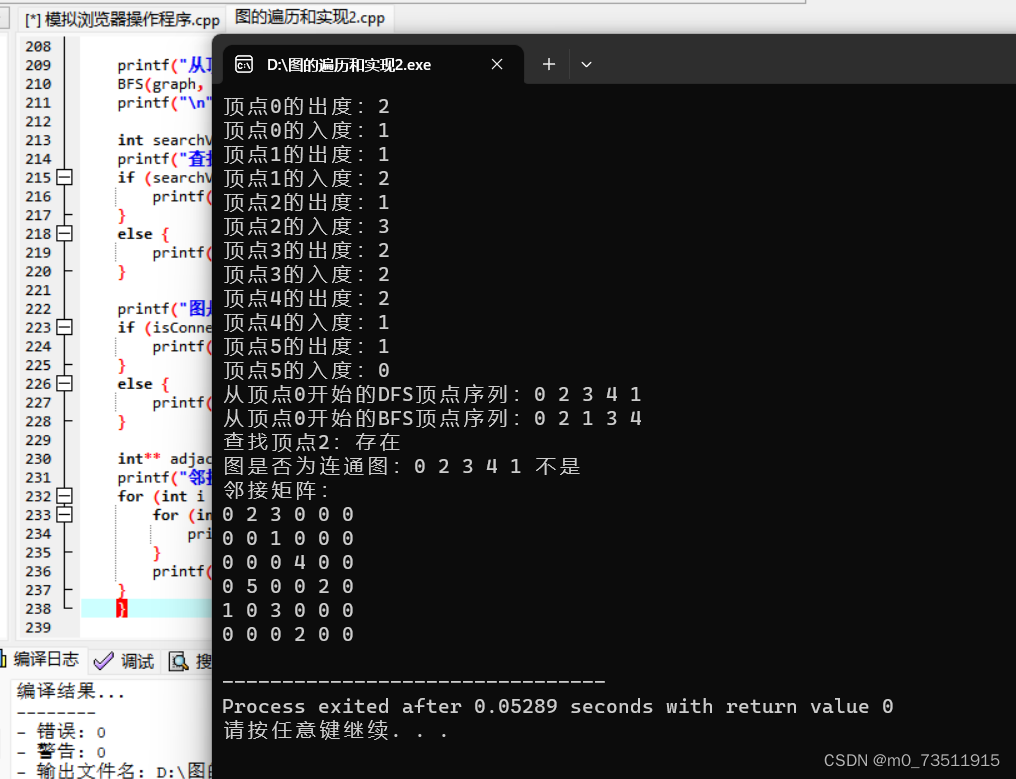
3.4.2测试结果:
4.八皇后问题
4.1问题描述
八皇后问题是一个古老而著名的问题,它是回溯算法的典型例题。该问题是 19 世纪德国著名数学家高斯于 1850 年提出的:在 8 行 8 列的国际象棋棋盘上摆放着 8 个皇后。若两个皇后位于同一行、同一列或同一对角线上,则称为它们为互相攻击。在国际象棋中皇后是最强大的棋子,因为它的攻击范围最大,
4.2需求分析
编程解决八皇后问题。在 8×8 的棋盘上,放置 8 个皇后。要求使这8 个皇后不能相互攻击,即每一横行、每一列,每一对角线上均只能放置一个皇后,求出所有可能的方案,输出这些方案,并统计方案总数。
4.3算法设计与实现
4.3.1.设计思路
因为八个皇后每一行只能有一个占据东宫的位置,所以我们只需要定义一个一维数组,每一个数字来表示皇后所在的列数即可。我们在每摆放一个新的皇后时都要与前面的皇后进行if语句的判断,确保她们不会再同一行上,不会在直角线上(成45°或135°)(定义的一维数组已经保证每一行只会有一个皇后,如果if不成立,则返回上一个皇后的位置重新选择)。
4.3.2主要函数说明及源程序
#include<stdio.h>
int main()
int count = 0;//计数器,每成功摆放一次记一次
for (int q1 = 0; q1 < 8; q1++)
{
for (int q2 = 0; q2 < 8; q2++)
{
if (q1 == q2 || q1 == q2 + 1 || q1 == q2 - 1)
{
continue;
}
for (int q3 = 0;q3 < 8; q3++)
{
if (q1 == q3 || q1 == q3 + 2 || q1 == q3-2
|| q2 == q3 || q2 == q3 + 1|| q2 == q3 - 1)
{
continue;
}
for (int q4 = 0; q4 < 8; q4++)
{
if (q1 == q4 || q1 == q4 + 3 || q1 == q4 - 3
|| q2 == q4 || q2 == q4 + 2|| q2 == q4- 2
|| q3 == q4 || q3 == q4 + 1 || q3== q4- 1)
{
continue;
}
for (int q5 = 0; q5 < 8; q5++)
{
if (q1 == q5 || q1 == q5 + 4 || q1 == q5 - 4
|| q2 == q5 || q2 == q5 + 3|| q2 == q5 - 3
|| q3 == q5 || q3 == q5 + 2 || q3 == q5- 2
|| q4 == q5 || q4 == q5 + 1 || q4 == q5 - 1)
{
continue;
}
for (int q6 = 0; q6 < 8; q6++)
{
if (q1 == q6 || q1 == q6 + 5 || q1 == q6 - 5
|| q2 == q6 || q2 == q6 + 4 || q2 == q6 - 4
|| q3 == q6 || q3 == q6 + 3 || q3 == q6 - 3
|| q4 == q6 || q4 == q6 + 2 || q4 == q6 - 2
|| q5 == q6 || q5 == q6 + 1 || q5 == q6 - 1)
{
continue;
}
for (int q7 = 0; q7 < 8; q7++)
{
if (q1 == q7 || q1 == q7 + 6 || q1 == q7 - 6
|| q2 == q7 || q2 == q7 + 5 || q2 == q7 - 5
|| q3 == q7 || q3 == q7 + 4 || q3 == q7 - 4
|| q4 == q7 || q4 == q7 + 3 || q4 == q7 - 3
|| q5 == q7 || q5 == q7 + 2 || q5 == q7 - 2
|| q6 == q7 || q6 == q7 + 1 || q6 == q7 - 1)
{
continue;
}
for (int q8 = 0; q8 < 8; q8++)
{
if (q1 == q8 || q1 == q8 + 7 || q1 == q8 - 7
|| q2 == q8 || q2 == q8 + 6 || q2 == q8 -6
|| q3 == q8 || q3 == q8 + 5 || q3 == q8 -5
|| q4 == q8 || q4 == q8 + 4 || q4 == q8 -4
|| q5 == q8 || q5 == q8 + 3 || q5 == q8 -3
|| q6 == q8 || q6 == q8 + 2 || q6 == q8 -2
|| q7 == q8 || q7 == q8 + 1 || q7 == q8 -1)
{
continue;
}
count++;
printf("%d,%d,%d,%d,%d,%d,%d,%d\n", q1, q2, q3, q4,q5, q6, q7, q8);
}
}
}
}
}
}
}
}
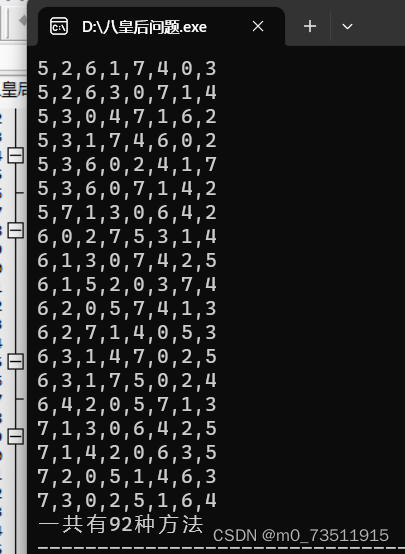
printf("一共有%d种方法", count);
return 0;
}4.4 调试分析与结果测试
4.4.1调试分析
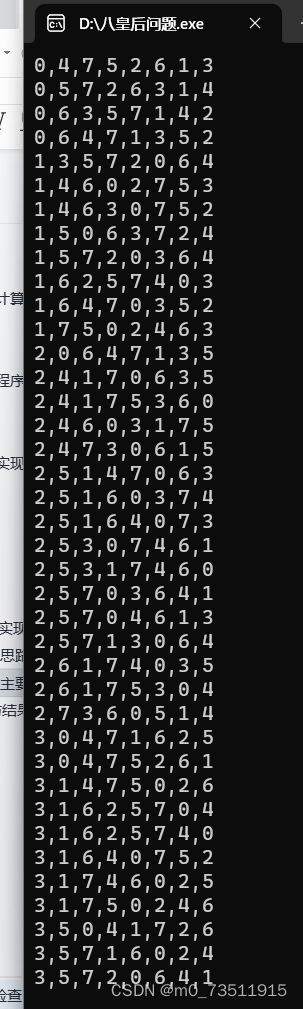
运行环境存在问题,在Dev C++中运行出现问题,结果出现遗漏
4.4.2测试结果:
5.木棒加工问题
5.1问题描述
现有 n 根木棒,已知它们的长度和重量,要用一部木工机一根一根地加工这些木棒。该的准备时间如下:
- 第一根木棒需要 1 分钟的准备时间。
(2)在加工完一根长为 lenth,重为 weight 的木棒之后,接着加工一根长为lenth'(lenth<=lenth'),重为 weight'(weight<= weight')的木棒是不需要任何准备时间的。否则需要一分钟的准备时间。
5.2需求分析
给定 n(1<n≤5000)根木棒,已知它们的长度和重量,请编写程序:找到加工完所有的木棒所需的最少准备时间,以及加工这些木棒的顺序。
5.3算法设计与分析
5.3.1设计思路
先对n根木棒按照长度进行全局排序,得到了一个长度有序而重量无序的序列(贪心先按长度排序)。\n再在每一个同一长度序列中,对重量进行局部排序。至此,长度和重量都是有序的。\n最长单调递增子序列的个数(采用动态规划),即为最终的答案。
5.3.2主要函数说明及源程序
void sort_length(int n) //排序算法
void sort_weight(int n) //同一长度内进行排序
【源程序】
#include <iostream>
#include <malloc.h>
#define max 5001
typedef struct{
int length, weight;
}boat;
boat b[max];
int count = 0;
using namespace std;
void sort_length(int n){
//排序算法
int i, j;
boat x;
for(i=1; i<=n; i++){
for(j=1; j<=n-i; j++){
if(b[j].length >= b[j+1].length){
x = b[j];
b[j] = b[j+1];
b[j+1] = x;
}
}
}
}
void sort_weight(int n){
boat x;
int i=1, j=1, p=0;
int k, s;
//同一长度内进行排序
for(i=1; i<=n; i++){
x = b[i];
j = i+1;
while(b[i].length == b[j].length){
j++;
}
p = 0;
for(k=i; k<j; k++){
//冒泡排序
for(s=i; s<j-p-1; s++){
if(b[s].weight >= b[s+1].weight){
x = b[s];
b[s] = b[s+1];
b[s+1] = x;
}
}
p++;
}
i = j-1;
}
for(i=1; i<=n; i++){
printf("%d %d\n", b[i].length, b[i].weight);
}
//排序完成
for(i=1; i<=n; i++){
k=i;
for(j=i+1; j<=n; j++){
if(b[i].length == b[j].length){
i = j;continue;
}
if(b[i].weight <= b[j].weight){
i = i+1;
x = b[j];
//元素后移
for(s=j; s>i; s--){
b[s] = b[s-1];
// printf("%d %d\n", b[s].length, b[s].weight);
}
b[i] = x;
}
}
count++;
printf("\n每一次加工的木棒\n");
for(; k<=i; k++){
printf("%d %d\n", b[k].length, b[k].weight);
}
}
printf("\n总共所需要的时间:%dmin\n", count);
}
int main(){
int n;
int i;
printf("请输入木棒总数:");
scanf("%d", &n);
printf("请输入木棒的长度和重量:");
for(i=1;i<=n;i++){
scanf("%d%d", &b[i].length, &b[i].weight);
}
printf("先按照长度进行排序。\n");
sort_length(n);
for(i=1; i<=n; i++){
printf("%d %d\n", b[i].length, b[i].weight);
}
printf("\n再在排好序的基础上按照重量排序。\n");
sort_weight(n);
return 0;
}5.4调试分析与结果测试
5.4.1调试分析
1.输入数据的格式错误:如果输入的木棒数量小于等于1或者大于5000,或者木棒的长度和重量不符合要求,程序可能无法正确处理这些数据。
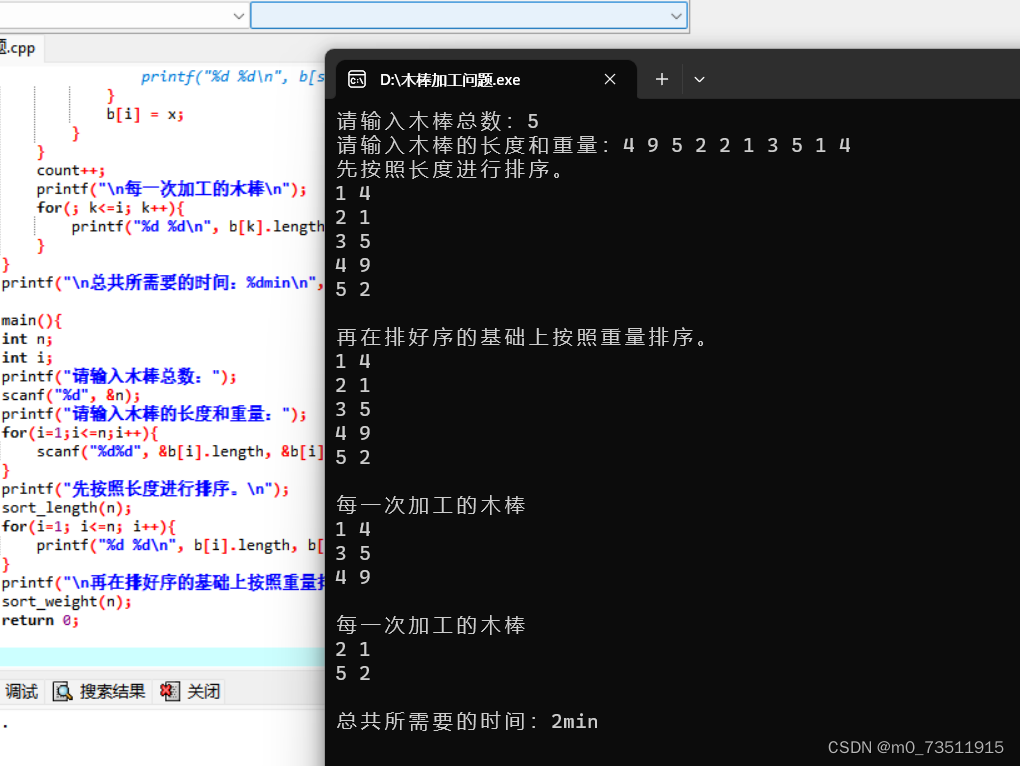
5.4.2测试结果:
三.课程设计总结
此次课程设计的题目可以说经典但是有点难度,主要体现在对于题目的理解和运用程序难以实现,在程序运行过程中还出现了包括编译环境在内的一系列问题,。我参照了网上的很多代码,几乎都需要自己的理解加上改写,这对于我是非常大的难题。好在班上有和我选一样的题的同学,这使我们可以一起探讨关于编程以及算法设计上的问题。也帮我解决了课程设计中的绝大多数问题。与此同时,经过这次的课程设计,我的对于程序的编写和改写能力得到了明显的提高,对结果的分析能力,资料搜集、阅读及整理能力,以及良好的沟通、表达能力都显著提升。也加深对常用数据结构理论知识的理解,能够运用各种数据结构与算法,独立分析、设计、解决问题。通过良好的文字、口头等沟通方式,表达个人对系统设计、实施及测试结论等方面的见解。
- 谭浩强.c程序设计(第二版)北京:清华大学出版社,2004
- 严蔚敏,吴伟民.数据结构.北京:清华大学出版社,2005
- 林劼,刘震,陈端兵等.数据结构与算法[M].北京大学出版社,2019.
陈锐,张志锋,马军霞.数据结构与算法详解[M]