先总体说下题型，共有20道选择题，4道简答题，3道编程题和1道扩展题，题目都比较简单，限时一小时完成。

一、选择题

选择题非常简单，都是基础题，什么死锁发生的条件、HashMap和HashSet查找插入删除的时间复杂度、Thread类和Runnable接口、排序复杂度比较、建堆调整堆等等，具体的也记不得了。

二、简答题

1. 简述Servlet的生命周期

2. 写出至少8个Java常用的包名称

3. Overload和Override的区别，Overloaded方法能不能修改返回值类型？

4. 不用中间变量交换a和b的值

三、编程题

1. 有N个人围一圈依次报数，数到3的人出列，问当只剩一个人时他原来的位子在哪里？

2. 有两个已递增有序的单链表pLinkList和qLinkList，将这两个链表合并成一个递增有序的链表，请自己定义单链表的结构。

3. 具体题目不记得，大概意思就是：从N个数中随机抽取出M个数(M < N)，为了使抽取比较均匀，请自己定义抽取函数使得抽取的数既均匀又尽量随机。

四、扩展题

具体题目也记不清了，一大堆，大概意思是：有一个海量日志库，里面的每条日志记录都有相应的关键词和访问次数，但记录是无序的，为了挖掘客户偏好，需要找出前N个最高访问次数的日志记录，请设计算法尽量使时间复杂度和空间复杂度最低。

下面是我自己写的答案，不一定正确，欢迎大家批评指定和提出自己更好的想法和意见：

二、简答题

1. 简述Servlet的生命周期

答：Web容器加载servlet，生命周期开始，通过调用servlet的的init()方法进行servlet的初始化，通过调用service()方法实现，根据请求的不同调用不同的doGet()和doPost()方法，结束服务，web容器调用servlet的destroy()方法。

一个servlet的生命周期由部署servlet的容器控制，当一个请求映射到一个servlet时，容器执行下步骤：

1.加载servlet类

2.创建一个servlet类的实例

3.调用init初始化servlet实例，

4.调用service方法，传递一个请求和响应对象

5.容器要移除一个servlet，调用servlet的destroy方法结束该servlet

2. 写出至少8个Java常用的包名称

答：答出以下的任意8个就行了

1.java.langJava编程语言的基本类库

2.java.applet创建applet需要的所有类

3.java.awt创建用户界面以及绘制和管理图形、图像的类

4.java.io通过数据流、对象序列以及文件系统实现的系统输入、输出

5.java.net用于实现网络通讯应用的所有类

6.java.util集合类、时间处理模式、日期时间工具等各类常用工具包

7.java.sql访问和处理来自于Java标准数据源数据的类

8.java.test以一种独立于自然语言的方式处理文本、日期、数字和消息的类和接口

9.java.security设计网络安全方案需要的一些类

10.java.beans开发Java Beans需要的所有类

11.java.math简明的整数算术以及十进制算术的基本函数

12.java.rmi与远程方法调用相关的所有类

3. Overload和Override的区别，Overloaded方法是否可以改变返回值类型？

答：Overload是重载的意思，Override是覆盖的意思，也就是重写。

(1)重载Overload表示同一个类中可以有多个名称相同的方法，但这些方法的参数列表各不相同(即参数个数或类型不同)，重载发生在同一个类中。

(2)重写Override表示子类中的方法可以与父类中的某个方法的名称和参数完全相同，通过子类创建的实例对象调用这个方法时，将调用子类中的定义方法，这相当于把父类中定义的那个完全相同的方法给覆盖了，这也是面向对象编程的多态性的一种表现。子类覆盖父类的方法时，只能比父类抛出更少的异常，或者是抛出父类抛出的异常的子异常，因为子类可以解决父类的一些问题，不能比父类有更多的问题。子类方法的访问权限只能比父类的更大，不能更小。如果父类的方法是private类型，那么，子类则不存在覆盖的限制，相当于子类中增加了一个全新的方法。重写发生在不同的类(父类和子类)中。

(3)至于Overloaded的方法是否可以改变返回值的类型这个问题，要看你倒底想问什么呢？这个题目很模糊。如果几个Overloaded的方法的参数列表不一样，它们的返回者类型当然也可以不一样。但我估计你想问的问题是：如果两个方法的参数列表完全一样，是否可以让它们的返回值不同来实现重载Overload。这是不行的，我们可以用反证法来说明这个问题，因为我们有时候调用一个方法时也可以不定义返回结果变量，即不要关心其返回结果，例如，我们调用map.remove(key)方法时，虽然remove方法有返回值，但是我们通常都不会定义接收返回结果的变量，这时候假设该类中有两个名称和参数列表完全相同的方法，仅仅是返回类型不同，java就无法确定编程者倒底是想调用哪个方法了，因为它无法通过返回结果类型来判断。

4. 不用中间变量交换a和b的值

答：很多种方法，我这里给出最简单的：

a = a + b;

b = a - b;

a = a - b;

三、编程题

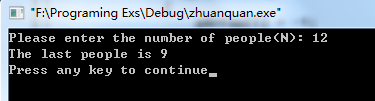
1. 有N个人围一圈依次报数，数到3的倍数的人出列，问当只剩一个人时他原来的位子在哪里？

解答：经典的转圈踢人问题，好吧专业一点，约瑟夫环问题，相信大家都会，下面给我的code：

intmain()

{intN, i, j;

printf("Please enter the number of people(N):");

scanf("%d", &N);int *pArray = (int *)malloc(sizeof(int) *N);int count = 0;//这里编号为0 ~ N - 1

for(i = 0; i < N; i++)

{

pArray[i]=i;

}for(i = 0, j = 0; i < N; i = (i + 1) %N)

{if(pArray[i] != -1)

{

j++;if(j % 3 == 0)

{

pArray[i]= -1;

count++;if(count ==N)

{

printf("The last people is %d\n", i);break;

}

}

}

}return 0;

}

好吧，我承认我的算法很臃肿，完全是模拟了整个游戏过程，时间复杂度为O(mn)，这里m=3，网上有个大牛给出了归纳数学的方法，具体方法如下：

为了讨论方便，先把问题稍微改变一下，并不影响原意：

问题描述：n个人(编号0~(n-1))，从0开始报数，报到(m-1)(这里m=3)的退出，剩下的人继续从0开始报数，求最后剩下一个人的编号。

我们知道第一个人(编号一定是m%n-1) 出列之后，剩下的n-1个人组成了一个新的约瑟夫环(以编号为k=m%n的人开始):

k  k+1  k+2  ... n-2, n-1, 0, 1, 2, ... k-2并且从k开始报0。

现在我们把他们的编号做一下转换：

k     --> 0

k+1   --> 1

k+2   --> 2

...

...

k-2   --> n-2

k-1   --> n-1

变换后就完完全全成为了(n-1)个人报数的子问题，假如我们知道这个子问题的解：例如x是最终的胜利者，那么根据上面这个表把这个x变回去不刚好就是n个人情况的解吗？！！变回去的公式很简单，相信大家都可以推出来：x'=(x+k)%n

如何知道(n-1)个人报数的问题的解？对，只要知道(n-2)个人的解就行了。(n-2)个人的解呢？当然是先求(n-3)的情况 ---- 这显然就是一个倒推问题！好了，思路出来了，下面写递推公式：

令f[i]表示i个人玩游戏报m退出最后胜利者的编号，最后的结果自然是f[n]

递推公式

f[1]=0;

f[i]=(f[i-1]+m)%i;  (i>1)

有了这个公式，我们要做的就是从1-n顺序算出f[i]的数值，最后结果是f[n]。因为实际生活中编号总是从1开始，我们输出f[n]+1

由于是逐级递推，不需要保存每个f[i]，程序也是异常简单：

#include #include

intmain()

{int N, i, s = 0;

printf("Please enter the number of people(N):");

scanf("%d", &N);for (i = 2; i <= N; i++)

{

s= (s + 3) %i;

}

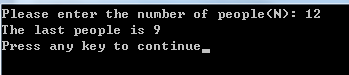
printf ("The last people is %d\n", s);return 0;

}

这个算法的时间复杂度为O(n)，相对于模拟算法已经有了很大的提高。算n，m等于一百万，一千万的情况不是问题了。可见，适当地运用数学策略，不仅可以让编程变得简单，而且往往会成倍地提高算法执行效率。数学确实很重要啊！！！

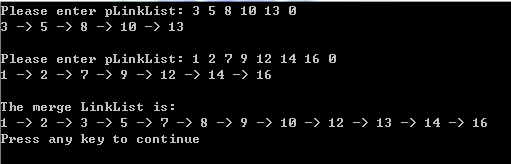
2. 有两个已递增有序的单链表pLinkList和qLinkList，将这两个链表合并成一个递增有序的链表，请自己定义单链表的结构。

解答：同样很经典，不用多说，直接上我自己的code(不是最好的)：

#include

using namespacestd;structLinkList {intdata;

LinkList*next;

};

LinkList*createList() {

LinkList*head = NULL, *p, *q;intdata;

cin>>data;while(data) {

p= newLinkList;

p->data =data;

p->next =NULL;if(head ==NULL) {

head=p;

q=head;

}else{

q->next =p;

q=p;

}

cin>>data;

}returnhead;

}//合并后的链表放在pLinkList中

void merge(LinkList *&pLinkList, LinkList *qLinkList) {

LinkList*pre, *p, *q;

pre=NULL;

p=pLinkList;

q=qLinkList;while(p != NULL && q !=NULL) {if(p->data < q->data)

{

pre=p;

p= p->next;

}else{//如果p第一个结点大于q，则改变合并后头结点为q

if(pre ==NULL)

{

pLinkList=q;

}else{

pre->next =q;

}

pre=q;

q=q->next;

pre->next =p;

}

}//最后不要忘了qLinkList剩余的大结点

if(q !=NULL)

{

pre->next =q;

}

}void print(LinkList *l) {

LinkList*p =l;while(p !=NULL) {if(p->next ==NULL) {

cout<< p->data;break;

}

cout<< p->data << "->";

p= p->next;

}

cout<

}intmain() {

cout<< "Please enter pLinkList:";

LinkList*pLinkList =createList();

print(pLinkList);

cout<< "\nPlease enter pLinkList:";

LinkList*qLinkList =createList();

print(qLinkList);

merge(pLinkList, qLinkList);

cout<< "\nThe merge LinkList is: \n";

print(pLinkList);return 0;

}

3. 具体题目不记得，大概意思就是：从N个数中随机抽取出M个数(M < N)，为了使抽取比较均匀，请自己定义抽取函数使得抽取的数既均匀又尽量随机。

解答：当时时间太急了，没来得及多想，做法很傻：从1 ~ M*N中随机抽取一个数字，然后mod (N + 1)，求得的值为N个数中的下标，再根据此下标去N个数中取，重复M次即可。假如这N个数存在数组nArray[]中，抽取的M个数存在数组mArray[]中，伪代码描述如下：

for(int i = 0; i < M; i++)

{int index = Random(M * N) %N;

mArray[i]=nArray[index];

}

由于觉得这个算法实在是不好，就懒得测试了，大家有好想法的赶紧提出来吧。

四、扩展题

具体题目也记不清了，一大堆描述，大概意思是：有一个海量日志库，里面的每条日志记录都有相应的关键词和访问次数，但记录是无序的，为了挖掘客户偏好，需要找出前N个最高访问次数的日志记录，请设计算法尽量使时间复杂度和空间复杂度最低。

解答：典型的Top K问题，我用的算法也是大家都知道的，大致描述下思路：假如关键词和访问次数成一个记录结构体，维护一个有N个该结构体的小根堆，初始化为N个日志记录的关键词和访问次数(建堆算法)，每次有新的记录时，将该记录的访问次数与小根堆的堆顶元素进行比较，如果大于堆顶元素则与堆顶元素交换记录，然后调整堆结构使其重新为一个小根堆，否则置之不理。当所有记录遍历完后，所有的堆元素就是所要求的前N个最高访问次数的日志记录。时间复杂度为O(MlgN)，不知道自己分析的对不对，完全是自以为是的想法，如果大家有更好的算法欢迎提出！