1.补充题(三)果园篱笆问题
1.1问题描述
某大学ACM集训队,不久前向学校申请了一块空地,成为自己的果园。全体队员兴高采烈的策划方案,种植了大批果树,有梨树、桃树、香蕉……。后来,发现有些坏蛋,他们暗地里偷摘果园的果子,被ACM 集训队队员发现了。因此,大家商量解决办法,有人提出:修筑一圈篱笆,把果园围起来,但是由于我们的经费有限,必须尽量节省资金,所以,我们要找出一种最合理的方案。由于每道篱笆,无论长度多长,都是同等价钱。所以,大家希望设计出来的修筑一圈篱笆的方案所花费的资金最少。有人己经做了准各工序,统计了果园里果树的位置,每棵果树分别用二维坐标来表示,进行定位。现在,他们要求根据所有的果树的位置,找出一个n边形的最小篱笆,使得所有果树都包围在篱笆内部,或者在篱笆边沿上。
本題的实质:凸包问题。请使用蛮力法和分治法求解该问题,
1、至少用两种方法设计该问题的,
2、用程序实现两种算法,并给出两算法运行结果的比较,要有图形化的界面
3、文档要求给出重要算法的算法设计的基本方法(分治,动态规划、贪心、
回溯等),选用这些设计方法的原因,给出该算法的伪代码,分析该算法的时间复杂度,给出算法实际运行的结果。
1.2解决问题所用的方法和基本思路
1.蛮力法:
(1)选用原因:
蛮力法是一种朴素的暴力搜索算法,它可以解决一些小规模的问题。在本问题中,蛮力法可以枚举所有可能的边,判断该边是否为凸包的一条边,最后得到凸包。虽然该算法的时间复杂度为O(n^3),但是当果树的数量比较小时,可以接受
(2)具体思路:
1. 对果树的坐标点进行排序,按照x坐标从小到大排序,如果x坐标相同,则按照y坐标从小到大排序。
2. 枚举所有可能的边,即对于每两个果树,判断是否能够构成凸包的一条边。
3. 对于每条边,判断其他果树是否在该边的左侧,如果都在左侧,则该边是凸包的一条边。
4. 将所有凸包的边保存下来,构成凸包。
最后,对凸包的顶点进行排序和去重操作,计算篱笆的长度即可。
2.分治法:
(1)选用原因:
在求解凸包的问题中,分治法是一种常用的解法。其基本思路是将问题分成若干个子问题,对每个子问题递归地求解,最后将子问题的解合并起来得到原问题的解.对于凸包问题,可以使用分治法来求解。具体地,我们可以将所有的点按照横坐标排序,然后选取横坐标最小和最大的两个点作为凸包上的端点。将剩余的点按照它们与直线AB的位置关系分成两部分,分别对这两部分递归求解凸包。然后将这两个凸包合并起来得到最终的凸包
在合并两个凸包的过程中,我们需要找到离直线AB最远的点C和D,然后将CD加入到凸包中。由于两个凸包都是凸的,因此CD一定是这两个凸包的交点。因此,我们可以通过二分查找的方法来找到CD.
由于每次递归都会将问题规模缩小一半,因此该算法的时间复杂度为O(nlogn)。因此,分治法是一种非常高效的解决凸包问题的方法。
通过递归地将点集分成两部分,分别求出这两部分的凸包,然后再将这两个凸包合并成一个凸包。其中,求解凸包的算法采用的是 Graham 扫描法。在求解凸包的过程中,对于每个点,算法根据其与凸包上两个端点的位置关系,判断其是否应该被加入到凸包中。如果该点应该被加入到凸包中,则算法会递归地处理该点与凸包上其他点的位置关系,以保证凸包的正确性。最终,算法得到的凸包就是所求的篱笆顶点。
(2)具体思路如下:
首先将所有的果树按照横坐标排序,如果横坐标相同,则按照纵坐标排序。
然后采用分治法求解凸包。首先在所有果树中选择横坐标最小和最大的两个点A和B,将果树分为两部分,一部分在直线AB的上方,另一部分在直线AB的下方。
对于每一部分,递归地求解其凸包。对于求解凸包的过程,采用了单调链法。具体做法是,首先将最左边的两个点加入到凸包中,然后从第三个点开始,依次加入到凸包中。对于每个新加入的点P,如果它在当前凸包的右侧,就将凸包的末尾点不断弹出,直到该点在凸包的左侧,然后再将该点加入到凸包的末尾。这样就可以得到一个凸包。
对于两个子凸包的合并,采用了分治的思想。首先找到两个凸包上离直线AB最远的点C和D,将CD加入到凸包中,然后递归地对两个子凸包进行合并。
最后得到的凸包就是果园的最小篱笆。计算凸包上所有相邻点之间的距离之和,即为最小篱笆的长度。
1.3 采用的数据结构描述
(1)分治法:数组、结构体和递归
(2)蛮力法:结构体(struct node),数组:包括p数组和s数组
1.4算法描述:
- 蛮力法:
算法名称:蛮力法求解凸包问题
输入:待处理篱笆顶点的个数以及各顶点的坐标
输出:篱笆应该放置的位置以及最小篱笆长度
伪代码:
蛮力法求解最小包围凸多边形 brute_force_convex_hull(n):
对果树坐标点数组 p 进行排序操作,排序规则为 cmp 函数;
m = 0;
for i <- 0 to n-1:
for j <- i+1 to n-1:
flag = 1;
for k <- 0 to n-1:
If k!=1 &&k!=j:
if multi(p[i], p[j], p[k]) > 0:
flag = 0;
break;
If(flag):
将 p[i] 存储到 s[m++] 中;
将 p[j] 存储到 s[m++] 中;- 分治法:
算法名称:分治法求解凸包问题
输入:待处理篱笆顶点的个数以及各顶点的坐标
输出:篱笆应该放置的位置以及最小篱笆长度
伪代码:
求解点集的凸包的功能。其中,dhull 函数和 uhull 函数分别用于求解下半部分和上半部分的 凸包。在每个函数中,算法首先找到距离直线最远的点,并将其作为新的端点。然后,算法 根据该点与原来的端点的位置关系,将点集分成两部分,并递归地对这两部分求解凸包。最 终,将两个凸包合并即可得到整个点集的凸包。
convex_hull(n):
qsort(p, n, sizeof(struct node), cmp)//对坐标点按照cmp函数规则进行排序
dhull(0, n - 1)//遍历下半部分的坐标点,找到与直线相交但离直线最远的点,记录其索引为j。如 果j为-1,则直接将p[x]加入凸包点,否则,根据叉积的正负来确定上半部分和下半部分的起始点,并递归调用dhull和uhull函数。
uhull(0, n - 1)//同dhull()。
dhull(x, y):
j = -1
for i from x + 1 to y - 1:
if multi(p[x], p[y], p[i]) <= 0:
if dist(p[x], p[y], p[i]) > dis:
dis = dist(p[x], p[y], p[i])
j = i
if j == -1:
s[m++] <- p[x]
return
if multi(p[x], p[j], p[y]) < 0:
uh <- x
dh<-y
else:
uh<-y
dh <- x
dhull(dh, j)
uhull(uh, j)1.5算法的时间和空间复杂度
- 蛮力:
基本运算:计算两个向量的叉积和比较
基本运算重复次数:O(n3)
时间复杂度分析:
输入果树的坐标点:时间复杂度为O(n),其中n是果树的个数。
排序果树的坐标点:使用快速排序算法qsort,时间复杂度为O(nlogn)。
枚举所有可能的凸包顶点组合:三重循环,时间复杂度为O(n^3)。
判断一个点是否在凸包内:对于每个点,需要遍历所有其他点进行判断,时间复杂度为O(n)。
计算篱笆的长度:遍历凸包的顶点,时间复杂度为O(m),其中m是凸包的顶点数。
综上所述,整个算法的时间复杂度为O(n^3)。
空间复杂度分析:
果树的坐标点数组:占用O(n)的空间。
凸包的顶点数组:占用O(n)的空间,最坏情况下凸包的顶点数为n。
其他局部变量:占用常数空间。
综上所述,整个算法的空间复杂度为O(n)。
- 分治:
基本运算:计算两个向量的叉积、计算点到直线的距离、计算两点之间的距离,比较
基本运算重复执行次数:O(n)
时间复杂度:
对输入的点集进行排序:O(nlogn)
篱笆算法的时间复杂度:T(n)=2T(n/2)+O(n)根据主定理可得其时间复杂度: O(nlogn)
总的时间复杂度:O(nlogn)
空间复杂度:
输入点需要O(n) 的空间存储
函数调用栈需要:O(logn) 的空间。
输出凸包点集需要:O(n) 的空间存储。
总的复杂度:O(n) 的空间存储。
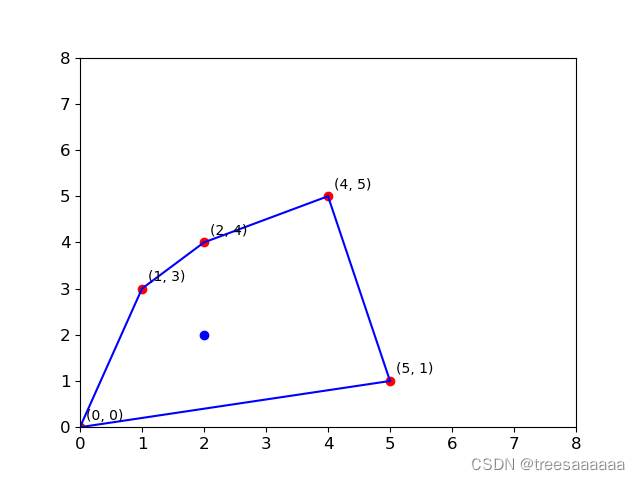
1.6算法实例:
最终结果图:
- 蛮力法:
输入:
输出:
代码:
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
struct node
{
double x, y;
};
struct node p[110], s[110];
int m;
double multi(struct node p1, struct node p2, struct node p3);//计算叉积
int cmp(const void *a, const void *b);对果树坐标点数组 p 进行排序操作
double dist(struct node p1, struct node p2, struct node p3);//求解点到直线的距离
void brute_force_convex_hull(int n);
int main()
{
int n, i;//n为果树的个数,i用于重复输入果树的顶点
m = 0;
printf("请输入果树的个数:\n");
scanf("%d", &n);
for (i = 0; i < n; i++)
{
printf("请输入第%d棵果树的坐标点:\n", i + 1);
scanf("%lf %lf", &p[i].x, &p[i].y); 输入第 i+1 棵果树的坐标点 p[i].x, p[i].y;
}
// 使用蛮力法求解最小包围凸多边形
brute_force_convex_hull(n);
printf("修筑一圈篱笆的最小方案为:\n");
// 对凸包顶点数组 s 进行排序和去重操作:
qsort(s, m, sizeof(struct node), cmp); //调用 qsort 函数对 s 数组进行排序,排序规则为 cmp 函数;qsort就是一个通过快速排序(一种排序方式)来实现任意类型数组排序的库函数。他所要的头文件为<stdlib.h>
int k = 0;
for (i = 1; i < m; i++) {
if (s[i].x != s[k].x || s[i].y != s[k].y) {
s[++k] = s[i];
}
}
m = k + 1;
double length = 0.0; // 篱笆的长度
for (i = 0; i < m; i++)
{
printf("(%lf, %lf)\n", s[i].x, s[i].y);
// 计算篱笆的长度
length += dist(s[i], s[(i + 1) % m], s[(i + 2) % m]);
}
printf("篱笆的长度为:%lf\n", length);
return 0;
}
double dist(struct node p1, struct node p2, struct node p3)
{
return sqrt(pow(p2.y - p1.y, 2) + pow(p1.x - p2.x, 2));
}
double multi(struct node p1, struct node p2, struct node p3)
{
return p1.x * p2.y + p3.x * p1.y + p2.x * p3.y - p3.x * p2.y - p2.x * p1.y - p1.x * p3.y;
}
int cmp(const void *a, const void *b)//
{比较函数 cmp(a, b):将结构体指针 a 和 b 转换为 struct node 类型的指针 pa 和 pb; 如果 pa->x 和 pb->x 相等,则返回 pa->y 和 pb->y 的大小关系;否则,返回 pa->x 和 pb->x 的大小关系;
struct node *pa = (struct node *)a;
struct node *pb = (struct node *)b;
if (pa->x == pb->x)
return pa->y < pb->y ? -1 : 1;
return pa->x < pb->x ? -1 : 1;
}
void brute_force_convex_hull(int n)
{
qsort(p, n, sizeof(struct node), cmp);
m = 0;
for (int i = 0; i < n; i++)
{
for (int j = i + 1; j < n; j++)
{
int flag = 1;
for (int k = 0; k < n; k++)
{
if (k != i && k != j)
{
if (multi(p[i], p[j], p[k]) > 0)
{
flag = 0;
break;
}
}
}
if (flag)
{
s[m++] = p[i];
s[m++] = p[j];
}
}
}
}- 分治法:
输入:
输出
代码:
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
#define PI acos(-1.0)
#define eps 1e-9
struct node
{
double x, y;
};
struct node p[110], s[110];//定义全局变量p和s,分别用于存储输入的坐标点和生成的凸包点。
int m;//用于记录凸包点的个数。
double multi(struct node p1, struct node p2, struct node p3);//计算叉积
int cmp(const void *a, const void *b);//用于排序坐标点。
double dist(struct node p1, struct node p2, struct node p3);//求解点到直线的距离
double distd(struct node a, struct node b);//计算两点之间的距离,计算两点 a 和 b 之间的欧几里得距离。
void convex_hull(int n);//用于计算凸包。
void uhull(int x, int y);//分别计算下半部分和上半部分的凸包。
void dhull(int x, int y);
int main()
{
int n, i;
double d;
m = 0;
printf("请输入待处理篱笆顶点个数:\n");
scanf("%d", &n);
for (i = 0; i < n; i++)
{
printf("请输入第%d个坐标点:\n", i + 1);
scanf("%lf %lf", &p[i].x, &p[i].y);
}
convex_hull(n);
double sum = 0;
for (i = 0; i < m; i++)
{
sum += distd(s[i], s[(i + 1) % m]);
}
printf("篱笆应放置点为:\n");
for (i = 0; i < m; i++)
{
printf("%lf, %lf\n", s[i].x, s[i].y);
}
printf("篱笆长度为:%lf\n", sum);
return 0;
}
double dist(struct node p1, struct node p2, struct node p3)
{
return fabs((p2.y - p1.y) * p3.x + (p1.x - p2.x) * p3.y + (p1.y - p2.y) * p1.x + (p2.x - p1.x) * p1.y) / sqrt(pow(p2.y - p1.y, 2) + pow(p1.x - p2.x, 2));
}
double multi(struct node p1, struct node p2, struct node p3)
{
return p1.x * p2.y + p3.x * p1.y + p2.x * p3.y - p3.x * p2.y - p2.x * p1.y - p1.x * p3.y;
}
int cmp(const void *a, const void *b)
{
struct node *pa = (struct node *)a;
struct node *pb = (struct node *)b;
if (fabs(pa->x - pb->x) <= eps)
return pa->y < pb->y ? -1 : 1;
return pa->x < pb->x ? -1 : 1;
}
double distd(struct node a, struct node b)
{
return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
void convex_hull(int n)
{
qsort(p, n, sizeof(struct node), cmp);//对坐标点进行排序。
dhull(0, n - 1);
uhull(0, n - 1);
}
void dhull(int x, int y)//遍历下半部分的坐标点,找到与直线相交但离直线最远的点,记录其索引为j。如果j为-1,则直接将p[x]加入凸包点。
否则,根据叉积的正负来确定上半部分和下半部分的起始点,并递归调用dhull和uhull函数。
{
int i, j, l, r;
double dis = -1;
j = -1;
if (x <= y)
{
l = x;
r = y;
}
else
{
l = y;
r = x;
}
for (i = l + 1; i < r; i++)
{
if (multi(p[x], p[y], p[i]) <= 0)
{
if (dist(p[x], p[y], p[i]) > dis)
{
dis = dist(p[x], p[y], p[i]);
j = i;
}
}
}
if (j == -1)
{
s[m++] = p[x];
return;
}
int uh, dh;
if (multi(p[x], p[j], p[y]) < 0)
{
uh = x;
dh = y;
}
else
{
uh = y;
dh = x;
}
dhull(dh, j);
uhull(uh, j);
}
void uhull(int x, int y)
{
int i, j, l, r;
double dis = -1;
j = -1;
if (x <= y)
{
l = x;
r = y;
}
else
{
l = y;
r = x;
}
for (i = l + 1; i < r; i++)
{
if (multi(p[x], p[y], p[i]) >= 0)
{
if (dist(p[x], p[y], p[i]) > dis)
{
dis = dist(p[x], p[y], p[i]);
j = i;
}
}
}
if (j == -1)
{
s[m++] = p[y];
return;
}
int uh, dh;
if (multi(p[x], p[j], p[y]) <= 0)
{
uh = x;
dh = y;
}
else
{
uh = y;
dh = x;
}
dhull(dh, j);
uhull(uh, j);
}