一.实验内容
- 最长公共子序列递归备忘录,动态规划算法比较
2.用程序实现算法,并画出程序运行时间与n*m的关系图,解释实验结果
二.实验过程及记录结果
1.递归求解代码:
int lcs1(char *X, char *Y, int m, int n)
{
if (m == 0 || n == 0) {
return 0;
} else if (X[m - 1] == Y[n - 1]) {
return 1 + lcs1(X, Y, m - 1, n - 1);
} else {
return max(lcs1(X, Y, m, n - 1), lcs1(X, Y, m - 1, n));
}
}
2.备忘录求解代码:
int lcs2(char *X, char *Y, int m, int n, int **memo)
{
if (memo[m][n] != -1) {
return memo[m][n];
}
if (m == 0 || n == 0) {
memo[m][n] = 0;
} else if (X[m - 1] == Y[n - 1]) {
memo[m][n] = 1 + lcs2(X, Y, m - 1, n - 1, memo);
} else {
memo[m][n] = max(lcs2(X, Y, m, n - 1, memo), lcs2(X, Y, m - 1, n, memo));
}
return memo[m][n];
}3.动态规划求解代码:
int lcs3(char *X, char *Y, int m, int n)
{
int i, j;
int **dp = (int **) malloc((m + 1) * sizeof(int *));
for (i = 0; i <= m; i++) {
dp[i] = (int *) malloc((n + 1) * sizeof(int));
}
for (i = 0; i <= m; i++) {
for (j = 0; j <= n; j++) {
if (i == 0 || j == 0) {
dp[i][j] = 0;
} else if (X[i - 1] == Y[j - 1]) {
dp[i][j] = 1 + dp[i - 1][j - 1];
} else {
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
int len3 = dp[m][n];
// 释放动态规划数组
for (i = 0; i <= m; i++)
{
free(dp[i]);
}
free(dp);
return len3;
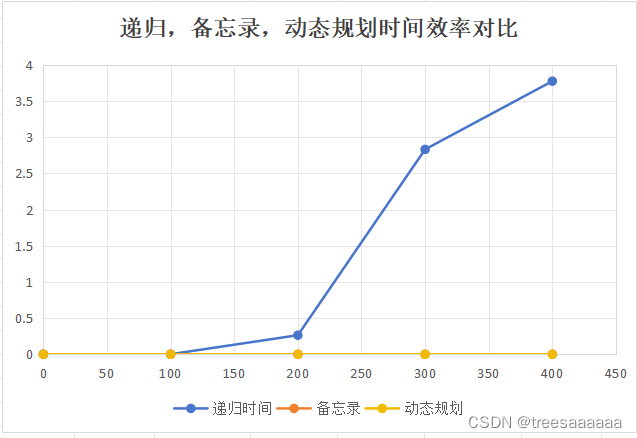
}4.递归,备忘录,动态规划求最大公共子序列的n*m(0<n*m<400)时间效率对比:
5.结果分析
实验结果:由运行结果可视化分析可以得出,当n逐渐增大后,递归所花费的时间明显高于备忘录和动态规划的时间。即动态规划的时间效率最高,备忘录第二,递归的时间效率最差。
原因分析:
- 递归:
* 递归的时间复杂度通常为 O(n * m),这是因为每次递归调用都需要对两个长度为 n 和 m 的序列进行比较,然后选择一个最优的选项。
* 递归的优点在于其简单性和直观性。我们可以很容易地理解和实现递归算法。
* 递归的缺点在于其时间复杂度较高,且在实际运行过程中可能会出现大量的重复计算,导致实际运行时间较长。 - 备忘录:
* 备忘录是一种优化递归的方法,它通过存储已经计算过的子问题的解来避免重复计算。使用备忘录后,时间复杂度可以降低到 O(n * m)。这是因为备忘录避免了重复计算,所以总体运行时间与直接计算递归的复杂度相同,但是实际运行时间可能会更短。
* 备忘录的优点在于其能够减少重复计算,提高算法效率。同时,备忘录也可以很方便地解决动态规划无法处理的问题,例如无法分解的问题。
* 备忘录的缺点在于其需要额外的空间来存储已经计算过的子问题的解,而且如果子问题的数量非常大,备忘录可能会占用大量的空间。
3.动态规划:
* 动态规划是解决最长公共子序列问题的最优方法,其时间复杂度为 O(n * m),与直接计算和备忘录相同。但是,动态规划的优点在于它不需要存储所有子问题的解,而只需要存储到达每个点的路径。因此,动态规划的内存使用通常比备忘录要小。
* 动态规划的优点在于其能够将原问题分解为子问题,并按照自底向上的顺序求解子问题,避免了递归的重复计算问题,且不需要额外的空间来存储子问题的解。此外,动态规划还可以很方便地处理无法分解的问题。
* 动态规划的缺点在于其需要较多的内存来存储中间状态的数据,如果输入序列的长度较大,动态规划可能会占用较多的内存。此外,动态规划的算法实现相对复杂一些,不如递归直观易懂。
六.总结
递归、备忘录和动态规划都有各自的优缺点。在选择使用哪种策略时,我们需要根据具体的问题和场景进行权衡。如果对算法的理解和实现较为简单,且对时间复杂度要求不高,可以选择递归;如果对算法效率和空间要求较高,且问题可以分解为子问题求解,可以选择动态规划;如果需要避免重复计算,且不需要额外的空间来存储子问题的解,可以选择备忘录。