一.实验内容
- 编写程序实现0-1背包问题的递归,备忘录,及动态规划的比较。
- 画出运行时间与n*C的曲线,并分析原因
二. 实验过程及记录结果
-
递归求解代码
int recursion(int n, int c) {
if (n == 0 || c == 0) {
return 0;
}
if (w[n] > c) {
return recursion(n-1, c);
}
int value1 = recursion(n-1, c);
int value2 = recursion(n-1, c-w[n]) + v[n];
return value1 > value2 ? value1 : value2;
}
2.备忘录求解代码
int memoization(int n, int c) {
if (n == 0 || c == 0) {
return 0;
}
if (memo[n][c] != -1) {
return memo[n][c];
}
int value;
if (w[n] > c) {
value = memoization(n-1, c);
} else {
int value1 = memoization(n-1, c);
int value2 = memoization(n-1, c-w[n]) + v[n];
value = value1 > value2 ? value1 : value2;
}
memo[n][c] = value;
return value;
}
3.动态规划求解代码
int dynamicProgramming() {
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= C; j++) {
if (w[i] > j) {
f[i][j] = f[i-1][j];
} else {
int value1 = f[i-1][j];
int value2 = f[i-1][j-w[i]] + v[i];
f[i][j] = value1 > value2 ? value1 : value2;
}
}
}
return f[N][C];
}4.完整代码
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#define N 15// 物品数量
#define W 15 // 背包容量
int w[N+1], v[N+1]; // 物品体积和价值
int f[N+1][W+1]; // 备忘录数组
int dp[N+1][W+1]; // 动态规划数组
// 递归解法
int thief(int i, int rest_w) {
if (i <= 0 || rest_w <= 0) {
return 0;
}
if (w[i] > rest_w) {
return thief(i-1, rest_w);
}
int value1 = thief(i-1, rest_w);
int value2 = thief(i-1, rest_w-w[i]) + v[i];
return value1 > value2 ? value1 : value2;
}
// 备忘录解法
int thief_memo(int i, int rest_w) {
if (i <= 0 || rest_w <= 0) {
return 0;
}
if (f[i][rest_w] >= 0) {
return f[i][rest_w];
}
if (w[i] > rest_w) {
f[i][rest_w] = thief_memo(i-1, rest_w);
} else {
int value1 = thief_memo(i-1, rest_w);
int value2 = thief_memo(i-1, rest_w-w[i]) + v[i];
f[i][rest_w] = value1 > value2 ? value1 : value2;
}
return f[i][rest_w];
}
// 动态规划解法
int thief_dp(int n, int w) {
for ( int i = 1; i <= n; i++) {
for (int j=1; j <= w; j++) {
if (j > w)
{
dp[i][j] = dp[i-1][j];
} else {
int value1 = dp[i-1][j];
int value2 = dp[i-1][j- w] + v[i];
dp[i][j] = value1 > value2 ? value1 : value2;
}
}
}
return dp[n][w];
}
int main() {
srand(time(NULL));
int capacity = rand() % (W+1); // 随机生成背包容量
printf("背包容量:%d\n", capacity);
for (int i = 1; i <= N; i++) {
w[i] = rand() % (capacity+1); // 随机生成物品体积
v[i] = rand() % 11; // 随机生成物品价值
printf("物品%d,体积=%d,价值=%d\n", i, w[i], v[i]);
}
// 递归解法
clock_t start_time = clock();
int max_value1 = thief(N, capacity);
clock_t end_time = clock();
printf("递归解法:最大总价值=%d,运行时间=%ldms\n", max_value1, end_time-start_time);
// 备忘录解法
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= W; j++) {
f[i][j] = -1;
}
}
start_time = clock();
int max_value2 = thief_memo(N, capacity);
end_time = clock();
printf("备忘录解法:最大总价值=%d,运行时间=%ldms\n", max_value2, end_time-start_time);
// 动态规划解法
start_time = clock();
int max_value3 = thief_dp(N, capacity);
end_time = clock();
printf("动态规划解法:最大总价值=%d,运行时间=%ldms\n", max_value3, end_time-start_time);
return 0;
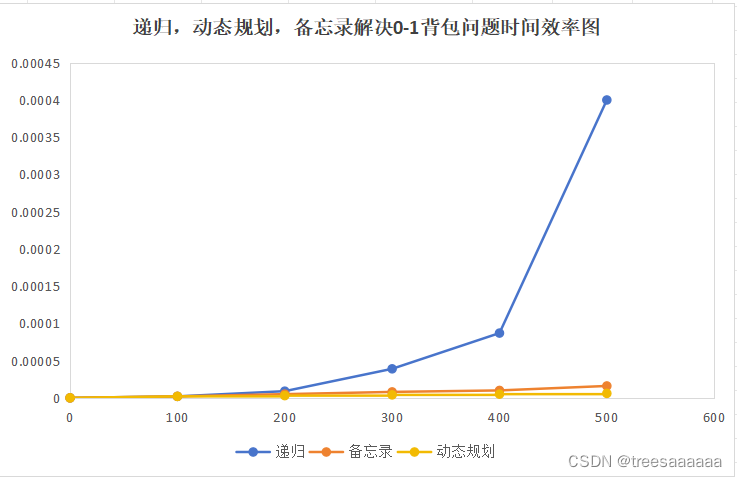
}5.递归,备忘录,动态规划求解0-1背包问题的n*C(0<n*m<500)时间效率对比
6.结果分析
实验结果:由运行结果可视化分析可以得出,当n*C逐渐增大后,递归所花费的时间明显高于备忘录和动态规划的时间。即动态规划的时间效率最高,备忘录第二,递归的时间效率最差。
原因分析:
(1)递归:
递归的思路是,对于给定的物品集合和背包容量,如果背包容量为0或者物品集合为空,那么背包的总价值也为0。否则,我们可以考虑所有物品的一种特定选择,即选取当前物品或者不选取当前物品。如果我们选取当前物品,那么我们需要在剩余的物品集合和剩余的背包容量上应用相同的递归过程;如果我们不选取当前物品,那么我们只需要在剩余的物品集合和剩余的背包容量上应用相同的递归过程。由于递归需要重复计算相同的子问题,所以它的时间复杂度是指数级的。具体来说,对于n个物品和背包容量为W的0-1背包问题,递归的时间复杂度是O(2^n * C)。
(2)备忘录:
备忘录的思路是,我们使用一个数组来存储已经计算过的子问题的解,这样当我们需要再次计算同一个子问题时,我们就可以直接使用存储在备忘录中的解,而不需要重新计算。备忘录方法可以避免递归中的重复计算,从而提高了效率。备忘录方法的时间复杂度是介于指数级和多项式级之间的。具体来说,对于n个物品和背包容量为W的0-1背包问题,备忘录的时间复杂度是O(nC)。虽然这比递归的效率高,但是当物品数量n或者背包容量W非常大时,备忘录方法仍然可能非常慢。
(3)动态规划:
动态规划的思路是,我们使用一个数组dp来存储子问题的解,并且当我们计算一个子问题时,我们更新这个数组的值。具体来说,dp[i][j]表示在前i个物品中选择总重量不超过j的情况下能够获得的最大价值。这样,当我们需要计算一个子问题时,我们只需要查看dp数组中已经计算过的子问题的解,而不是像备忘录方法那样需要存储所有的子问题的解。对于n个物品和背包容量为W的0-1背包问题,动态规划的时间复杂度是O(nW)。动态规划的时间复杂度与备忘录的时间复杂度相同,但是动态规划不需要像备忘录那样存储所有的子问题的解,因此在实际应用中动态规划通常比备忘录更有效。
7.总结
1. 递归的时间复杂度是指数级的,因为递归需要重复计算相同的子问题。这是导致递归在解决大规模0-1背包问题时效率低的主要原因。
2. 备忘录方法通过存储已经计算过的子问题的解来避免重复计算,从而提高了效率。但是,由于备忘录需要存储所有子问题的解,当物品数量n或者背包容量W非常大时,备忘录方法仍然可能非常慢。
3. 动态规划方法通过只存储需要的子问题的解来避免重复计算,从而提高了效率。动态规划的时间复杂度与备忘录相同,但是动态规划不需要存储所有的子问题的解,因此在处理大规模问题时通常更有效。