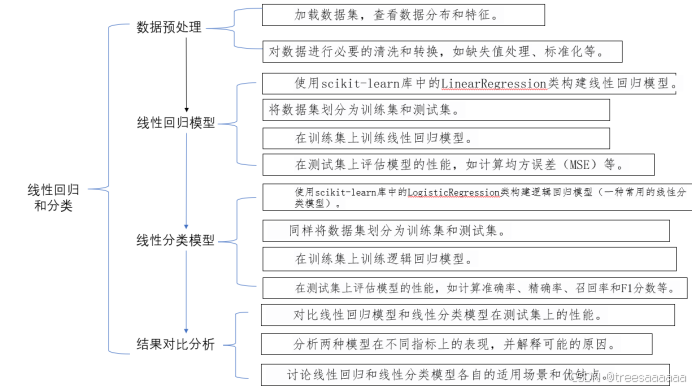
一、实验目的
本实验旨在通过实际编程实践,掌握线性回归和线性分类模型的基本原理和实现方法。通过对比两种模型在特定数据集上的表现,加深对机器学习算法的理解,并学习如何评估模型的性能。
二、实验环境
- 操作系统:Windows/Linux/MacOS
- 编程语言:Python
- 开发环境:Jupyter Notebook/PyCharm
- 库:NumPy, Pandas, Matplotlib, scikit-learn
三、实验数据集
本实验使用了一个包含两个类别(类别0和类别1)的模拟数据集。数据集包含特征变量和目标变量,用于训练和评估线性回归和线性分类模型。
四、实验步骤
- 数据预处理
- 加载数据集,查看数据分布和特征。
- 对数据进行必要的清洗和转换,如缺失值处理、标准化等。
- 线性回归模型
- 使用scikit-learn库中的LinearRegression类构建线性回归模型。
- 将数据集划分为训练集和测试集(如果需要)。
- 在训练集上训练线性回归模型。
- 在测试集上评估模型的性能,如计算均方误差(MSE)等。
- 线性分类模型
- 使用scikit-learn库中的LogisticRegression类构建逻辑回归模型(一种常用的线性分类模型)。
- 同样将数据集划分为训练集和测试集。
- 在训练集上训练逻辑回归模型。
- 在测试集上评估模型的性能,如计算准确率、精确率、召回率和F1分数等。
- 结果对比与分析
- 对比线性回归模型和线性分类模型在测试集上的性能。
- 分析两种模型在不同指标上的表现,并解释可能的原因。
- 讨论线性回归和线性分类模型各自的适用场景和优缺点。
- 实验目的
1.线性回归模型部分
(1)应用场景
预测房价:根据多个特征(如面积、卧室数量、位置等)预测房价。
销售额预测:根据广告支出、季节、市场趋势等特征预测未来的销售额。
温度预测:根据历史数据中的日期和时间特征预测未来的温度。
(2)原因
线性回归模型适用于预测一个连续变量(因变量)与一个或多个自变量之间的线性关系。在上述场景中,目标变量(如房价、销售额、温度等)都是连续的数值,这使得线性回归成为一个合适的选择。
2.逻辑回归模型部分
(1)应用场景
疾病诊断:根据病人的症状和体检数据预测是否患有某种疾病(如糖尿病)。
客户流失预测:根据客户的使用行为、服务反馈等数据预测客户是否会流失。
垃圾邮件分类:根据邮件内容的特征(如词频、链接数量等)预测邮件是否为垃圾邮件。
(2)原因
逻辑回归模型适用于二分类问题,即预测目标变量是两个类别之一。在上述场景中,目标变量(如是否患病、是否流失、是否为垃圾邮件)都是二元的,这使得逻辑回归成为一个合适的选择。此外,逻辑回归还提供概率输出,可以帮助我们更好地理解预测结果的置信度。
- 实验步骤
- 实验流程
2.实验结果反映的现实问题:
通过线性回归模型,我们可以得到特征(如时间、消费指数等)与目标变量(如物价)的关系。现实世界中,物价趋势受多种因素影响,包括经济发展水平、政策变化等。线性回归可以帮助我们量化这些关系,为政府和企业提供决策依据。例如:预测未来物价: 基于历史数据,预测未来某一时间点的物价。政策效果分析: 评估某一政策(如税收政策)对物价的影响。
通过上述模型,我们可以构建综合分析系统,预测和分析物价趋势与经济情况的关联性。例如:
(1)数据收集与预处理:
收集多年的经济数据,包括 GDP、失业率、通货膨胀率等。
收集相应年份的物价指数、消费指数等。
(2)模型建立与训练:
使用线性回归模型,分析各经济指标与物价指数的关系。
使用逻辑回归模型,将经济数据与物价变化分类(上涨、平稳、下跌)。
(3)模型应用:
预测未来物价趋势,为政府制定经济政策提供参考。
评估不同政策对物价的影响,帮助企业制定价格策略。
- 附源代码
# 导入线性回归模型
from sklearn.linear_model import LinearRegression # 线性回归模型用于预测一个或多个自变量与因变量之间的关系
# 打印标题,说明接下来是一个线性回归模型的训练例子
print("线性回归模型训练例子")
# 实例化一个线性回归模型对象
clf = LinearRegression()
# 使用三个样本点进行训练。这些点形成一条直线,所以线性回归模型可以完美地拟合它们
clf.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2]) # 训练数据,前两个列表是特征(x1, x2),第三个列表是目标值(y)
# 说明预期的线性方程,这里的注释仅用于说明,并非模型实际学到的方程
y = 0.5*x1 + 0.5*x2 # 线性方程(预测模型),但这只是假设,实际模型可能会学到不同的系数
# 使用训练好的模型对新的数据点 [3, 3] 进行预测
pre = clf.predict([[3, 3]]) # 预测数据[3, 3]的 y 值
# 打印模型的回归系数和截距
print("回归系数", clf.coef_) # 回归系数表示每个特征对目标变量的影响程度
print("截距", clf.intercept_) # 截距表示当所有特征都为 0 时,目标变量的预测值
# 打印数据[3, 3]的预测值
print("数据[3, 3]的预测值:", pre)
print("*****************")
# 导入逻辑回归模型类,它是 sklearn 库中用于解决分类问题的一个类
from sklearn.linear_model import LogisticRegression
# 导入 make_classification 函数,该函数用于生成模拟的分类数据集
# 它非常适合于测试机器学习算法
from sklearn.datasets import make_classification
# 导入 train_test_split 函数,该函数用于将数据集划分为训练集和测试集
# 在机器学习中,我们通常需要将数据集划分为这两部分来训练和评估模型
from sklearn.model_selection import train_test_split
# 导入 classification_report 函数,该函数用于评估分类模型的性能
# 它会输出每个类别的精确度、召回率、F1 分数等指标
from sklearn.metrics import classification_report
# 导入 numpy 库,它提供了大量的数学函数和工具来操作大型多维数组和矩阵
import numpy as np
# 使用 make_classification 函数来生成一个模拟的二分类数据集
# 参数解释:
# n_samples=100: 生成的样本数量为 100
# n_features=2: 每个样本的特征数量为 2
# n_informative=2: 所有特征都是信息性的(即都与目标变量 y 相关)
# n_redundant=0: 没有冗余的特征(即与目标变量 y 无关的特征)
# random_state=42: 设置随机数生成器的种子,以确保每次运行代码时生成的数据集相同
X, y = make_classification(n_samples=100, n_features=2, n_informative=2,
n_redundant=0, random_state=42)
# 使用 train_test_split 函数来划分数据集
# 参数解释:
# X, y: 要划分的特征矩阵和目标变量数组
# test_size=0.2: 测试集占整个数据集的比例为 20%
# random_state=42: 设置随机数生成器的种子,以确保划分的结果相同
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=42)
# 创建一个逻辑回归模型的实例
# 参数解释:
# solver='liblinear': 使用'liblinear'求解器来优化问题,它特别适合于小数据集
# random_state=42: 设置随机数生成器的种子,以确保模型训练的结果相同
clf = LogisticRegression(solver='liblinear', random_state=42)
# 使用训练集数据来拟合(训练)逻辑回归模型
# 参数解释:
# X_train, y_train: 训练集的特征矩阵和目标变量数组
clf.fit(X_train, y_train)
# 使用训练好的模型对测试集进行预测
# 参数解释:
# X_test: 测试集的特征矩阵
# 返回值:
# y_pred: 测试集上模型预测的目标变量数组
y_pred = clf.predict(X_test)
# 打印分类报告,该报告会展示模型的分类性能
print(classification_report(y_test, y_pred))
# 打印逻辑回归模型的系数(权重)
# 这些系数表示每个特征对模型预测结果的影响程度
print("回归系数(权重):", clf.coef_)
# 打印模型的截距
# 截距表示当所有特征都为 0 时,模型预测为正样本的概率的对数几率
print("截距:", clf.intercept_)
# 使用 predict_proba 方法获取测试集上每个样本属于各个类别的概率预测
# 对于二分类问题,这将返回两个概率值(对应于两个类别),它们的和应该接近 1
y_prob = clf.predict_proba(X_test)
print("预测概率:\n", y_prob)结果展示: