大家好呀，我是残念，希望在你看完之后，能对你有所帮助，有什么不足请指正！共同学习交流哦（不能私学，谁私学谁是）
本文由：残念ing原创CSDN首发，如需要转载请通知
个人主页：残念ing-CSDN博客，欢迎各位→点赞👍 + 收藏⭐️ + 留言📝
📣系列专栏：残念ing 的C++进阶系列专栏——CSDN博客

1.红黑树的概念：

红黑树是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。通过对任何一条从根到叶子的路径上各个着色方式的限制，红黑树确保么没有一条路径会比其他路径长出两倍(最长路径<=最短路径*2)，因此是接近平衡的。

2.红黑树的性质：

1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的，则它的两个孩子结点是黑色的（一条路径中没有连续的红色）
4. 对于每一个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点（每条路径上的黑色结点是相等的）
5. 每个叶子结点都是黑色的（此处的叶子结点是指空结点）

3.实现时需要注意的情况

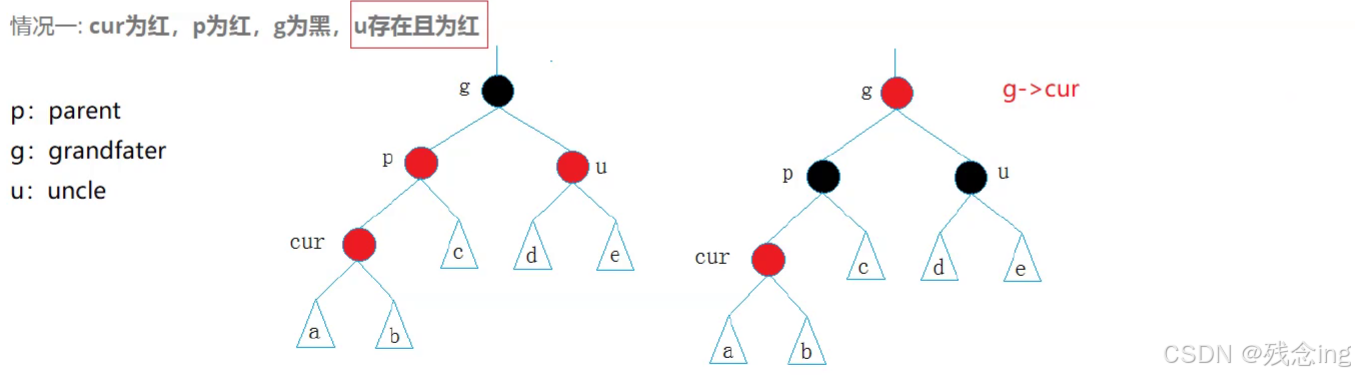
3.1 情况一：cur为红，p为红，g为黑，u存在且为红

解决办法：将p，u改成黑，将g改为红，然后把g当成cur，继续向上调整，如果g为根结点的话就不用变为红了，也就停止了

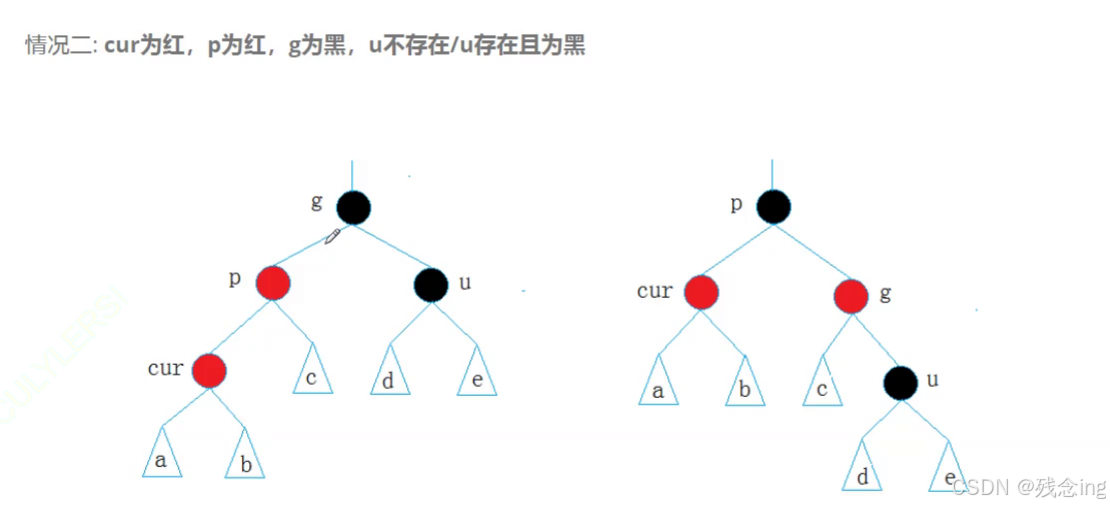
3.2 情况二：cur为红，p为红，g为黑，u不存在/u存在且为黑

3.2.1 u不存在

解决办法：
如果p为g的左孩子，cur为p的左孩子，则进行右单旋（以g为点），
如果p为g的右孩子，cur为p的右孩子，则进行左单旋，
旋转之后，p变为黑，g为红

3.2.2 u存在且为黑

解决办法：
p为g的左孩子，cur为p的右孩子，则进行左右双旋（以p为点左旋，以g为点右旋，然后将cur变为黑，g变为红）
p为g的右孩子，cur为p的左孩子，则进行右左双旋，
旋转之后，p变为黑，g为红

4 代码的实现

#pragma once
#pragma once
#include<iostream>
#include<assert.h>
using namespace std;


enum Color
{
	READ,
	BLAKE
};
template<class K, class V>
struct RBTreeNodes
{
	pair<K, V> _kv;
	RBTreeNodes<K, V>* _left;
	RBTreeNodes<K, V>* _right;
	RBTreeNodes<K, V>* _parent;
	Color _color;

	RBTreeNodes(const pair<K, V>& kv)
		: _kv(kv)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _color(READ)
	{}
};


template <class K, class V>

class RBTree
{
	typedef RBTreeNodes<K, V> NOde;
public:

	//添加
	bool Inster(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new NOde(kv);
			_root->_color = BLAKE;
			return true;
		}
		NOde* parent = nullptr;
		NOde* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;

			}
			else if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				return false;
			}
		}
		cur = new NOde(kv);
		cur->_color = READ;
		if (parent->_kv.first < kv.first)
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		cur->_parent = parent;
		//处理
		while (parent && parent->_color == READ)
		{
			NOde* grandfather = parent->_parent;
			if (grandfather->_left == parent)
			{
				//u存在且为红
				NOde* uncle = grandfather->_right;
				if (uncle && uncle->_color == READ)
				{
					parent->_color = BLAKE;
					uncle->_color = BLAKE;
					grandfather->_color = READ;

					cur = grandfather;
					parent = cur->_parent;
				}
				else if (uncle == nullptr || uncle->_color == BLAKE)
				{
					if (cur == parent->_left)
					{
						//右旋转
						RotateR(grandfather);
						parent->_color = BLAKE;
						grandfather->_color = READ;
					}
					if (cur == parent->_right)
					{
						//左右双旋转
						RotateL(parent);
						RotateR(grandfather);
						cur->_color = BLAKE;
						grandfather->_color = READ;
					}

					break;
				}
			}
			else if (grandfather->_right == parent)
			{
				NOde* uncle = grandfather->_left;
				if (uncle && uncle->_color == READ)
				{
					parent->_color = BLAKE;
					uncle->_color = BLAKE;
					grandfather->_color = READ;
					cur = grandfather;
					parent = cur->_parent;
				}
				else if (uncle == nullptr || uncle->_color == BLAKE)
				{
					if (cur == parent->_right)
					{
						//左旋转
						RotateL(grandfather);
						parent->_color = BLAKE;
						grandfather->_color = READ;

					}
					if (cur == parent->_left)
					{
						//右左双旋转
						RotateR(parent);
						RotateL(grandfather);
						cur->_color = BLAKE;
						grandfather->_color = READ;
					}
					break;
				}

			}
		}
		_root->_color = BLAKE;

		return true;
	}

	NOde* Find(const K& key)
	{
		NOde* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
			{
				cur = cur->_right;

			}
			else if (cur->_kv.first > key)
			{
				cur = cur->_left;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}

	void Inorder()
	{
		_Inorder(_root);
		cout << endl;
	}
	bool Delete(const K& key)
	{
		NOde* parent = nullptr;
		NOde* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
			{
				parent = cur;
				cur = cur->_right;

			}
			else if (cur->_kv.first > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//delete一个或0个孩子
				if (cur->_left == nullptr)
				{
					if (parent == nullptr)
					{
						_root = cur->_right;
					}
					else
					{
						if (parent->_left == cur)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}
					delete cur;
					return true;
				}
				if (cur->_right == nullptr)
				{
					if (parent == nullptr)
					{
						_root = cur->_left;
					}
					else
					{
						if (parent->_right == cur)
						{
							parent->_right = cur->_left;
						}
						else
						{
							parent->_left = cur->_left;
						}
					}
					delete cur;
					return true;
				}

				//两个孩子
				//右子树最小节点作为代替节点
				NOde* rightMinp = cur;
				NOde* rightMin = cur->_right;
				while (rightMin->_left)
				{
					rightMinp = rightMin;
					rightMin = rightMin->_left;
				}
				cur->_key = rightMin->_key;

				if (rightMinp->_left == rightMin)
					rightMinp->_left = rightMin->_right;
				else
					rightMinp->_right = rightMin->_right;

				delete rightMin;
				return true;
			}
		}
		return false;
	}

	bool IsBalance()
	{
		if (_root == nullptr)
			return true;

		if (_root->_color == READ)
		{
			return false;
		}

		// 参考值
		int refNum = 0;
		NOde* cur = _root;
		while (cur)
		{
			if (cur->_color == BLAKE)
			{
				++refNum;
			}

			cur = cur->_left;
		}

		return Check(_root, 0, refNum);
	}

private:

	bool Check(NOde* root, int blackNum, const int refNum)
	{
		if (root == nullptr)
		{

			if (refNum != blackNum)
			{
				cout << "存在黑色节点的数量不相等的路径" << endl;
				return false;
			}
			cout << blackNum << " " << refNum << endl;
			return true;
		}

		if (root->_color == READ && root->_parent->_color == READ)
		{
			cout << root->_kv.first << "存在连续的红色节点" << endl;
			return false;
		}

		if (root->_color == BLAKE)
		{
			blackNum++;
		}

		return Check(root->_left, blackNum, refNum)
			&& Check(root->_right, blackNum, refNum);
	}

	int _Height(NOde* root)
	{
		if (root == nullptr)
		{
			return 0;
		}
		int leftHeight = _Height(root->_left);
		int rightHeight = _Height(root->_right);
		return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
	}

	void RotateL(NOde* parent)
	{
		NOde* subR = parent->_right;
		NOde* subRL = subR->_left;

		parent->_right = subRL;
		if (subRL)
			subRL->_parent = parent;
		NOde* parentparent = parent->_parent;

		subR->_left = parent;
		parent->_parent = subR;

		if (parentparent == nullptr)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (parent == parentparent->_left)
			{
				parentparent->_left = subR;
			}
			if (parent == parentparent->_right)
			{
				parentparent->_right = subR;
			}
			subR->_parent = parentparent;
		}

	}
	void RotateR(NOde* parent)
	{
		NOde* subL = parent->_left;
		NOde* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;
		NOde* parentparent = parent->_parent;

		subL->_right = parent;
		parent->_parent = subL;

		if (parentparent == nullptr)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (parent == parentparent->_left)
			{
				parentparent->_left = subL;
			}
			if (parent == parentparent->_right)
			{
				parentparent->_right = subL;
			}
			subL->_parent = parentparent;
		}

	}

	void _Inorder(NOde* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_Inorder(root->_left);
		cout << root->_kv.first << "=" << root->_kv.second << "|";
		_Inorder(root->_right);
	}

private:
	NOde* _root = nullptr;
};

void TestAVLTree()
{
	RBTree<int, int> t;
	int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto e : a)
	{
		t.Inster({ e, e });
	}

	t.Inorder();
	cout << t.IsBalance() << endl;
}