贪心算法(Greedy Algorithm) 概述:
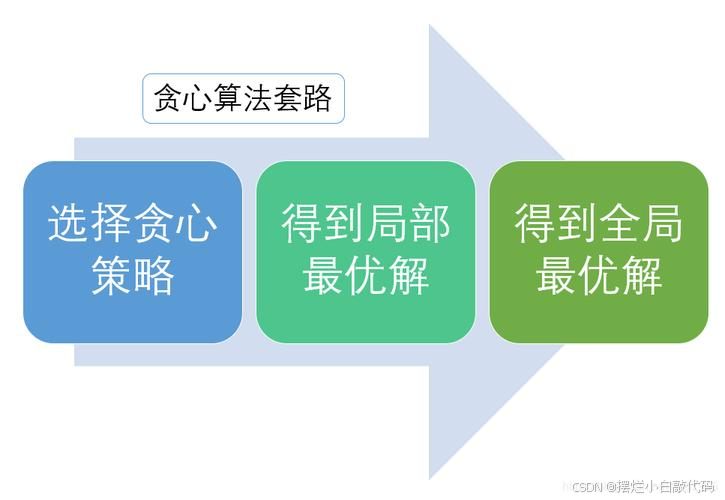
贪心算法是一种在求解最优化问题时采取的一种常用算法策略。贪心算法的基本思想是,每次选择当前情况下的局部最优解,并相信这个局部最优解能够导致全局最优解。贪心算法通过迭代的方式一步步地构建最优解,并不进行回溯。
贪心算法的一般步骤:
1. 将问题分解成多个子问题;
2. 对每个子问题,确定一个最优解;
3. 对每个子问题的最优解进行合并,得到原问题的最优解。
贪心算法的正确性需要满足两个条件:
1.最优子结构:问题的最优解能够由子问题的最优解组合而成。
2. 贪心选择性:通过局部最优选择能够得到全局最优解。
贪心算法适用的问题一般具有以下特点:
1. 子问题的最优解能够推导出原问题的最优解;
2. 子问题的最优解构成原问题的最优解时,原问题的最优解也能由它推导出。
贪心算法的优点是简单、高效,时间复杂度通常较低。然而,贪心算法并不适用于所有问题,有些问题需要使用其他更复杂的算法来求解。在使用贪心算法时,需要仔细分析问题的特点并证明贪心策略的正确性。
由于贪心是一种思想,没有具体的算法模板,而且贪心一般不会单独作为一种算法出现在题目中,一般会跟其他算法结合在一起出现。例如:动态规划、递归、高级数据结构等。在此基础上保证每一步时最优解的情况下就可以得到最优的答案。下面我们将以例题的形式让大家来了解这种思想。
例题一:
AcWing 3769. 移动石子
题目:
一共有 n 个箱子排成一排,从左到右依次编号为 1∼n。
其中,第 i 号箱子中放有 ai个石子。
现在,你可以进行最多 d 次操作。
每次操作可以将一个石子从一个箱子移动至另一个与其相邻的箱子里。
我们希望通过合理操作使得 1 号箱子内的石子数量尽可能大。
请问,这个最大可能值是多少?
输入格式
第一行包含整数 T,表示共有 T 组测试数据。
每组数据第一行包含两个整数 n和 d。
第二行包含 n 个整数 a1,a2,…,an。
输出格式
每组数据输出一行结果,表示答案。
数据范围
1≤T≤100,
1≤n,d≤100,
0≤ai≤100.
输入样例:
3
4 5
1 0 3 2
2 2
100 1
1 8
0
输出样例:
3
101
0解题思路:
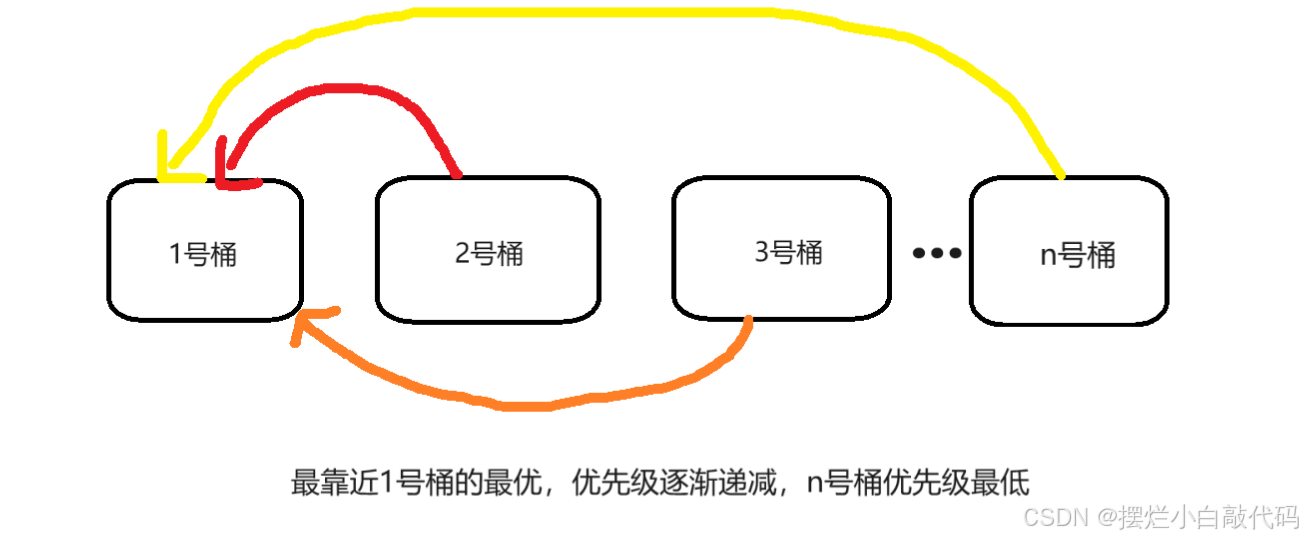
这个题很明显贪心思想,要让第一个箱子尽可能多的石子,在操作次数的限制下,我们最优解,要从第二个箱子开始贪心,第二个、第三个...,这样可以使操作次数尽可能的少。
AC代码:
#include<iostream>
using namespace std;
const int N=105;
int t,n,d;
int a[N];
int main(){
cin>>t;
while(t--){
cin>>n>>d;
for(int i=1;i<=n;i++)cin>>a[i];
int k=2;
while(d){
if(k>n)break;
if(d>=a[k]*(k-1)){
a[1]+=a[k];
d-=a[k]*(k-1);
}else{
a[1]+=d/(k-1);
d=0;
}
k++;
}
cout<<a[1]<<endl;
}
return 0;
}例题二:
洛谷 P1007 独木桥
题目背景
战争已经进入到紧要时间。你是运输小队长,正在率领运输部队向前线运送物资。运输任务像做题一样的无聊。你希望找些刺激,于是命令你的士兵们到前方的一座独木桥上欣赏风景,而你留在桥下欣赏士兵们。士兵们十分愤怒,因为这座独木桥十分狭窄,只能容纳 1 个人通过。假如有 2 个人相向而行在桥上相遇,那么他们 2 个人将无法绕过对方,只能有 1 个人回头下桥,让另一个人先通过。但是,可以有多个人同时呆在同一个位置。
题目描述
突然,你收到从指挥部发来的信息,敌军的轰炸机正朝着你所在的独木桥飞来!为了安全,你的部队必须撤下独木桥。独木桥的长度为 L,士兵们只能呆在坐标为整数的地方。所有士兵的速度都为 1,但一个士兵某一时刻来到了坐标为 0 或 L+1 的位置,他就离开了独木桥。
每个士兵都有一个初始面对的方向,他们会以匀速朝着这个方向行走,中途不会自己改变方向。但是,如果两个士兵面对面相遇,他们无法彼此通过对方,于是就分别转身,继续行走。转身不需要任何的时间。
由于先前的愤怒,你已不能控制你的士兵。甚至,你连每个士兵初始面对的方向都不知道。因此,你想要知道你的部队最少需要多少时间就可能全部撤离独木桥。另外,总部也在安排阻拦敌人的进攻,因此你还需要知道你的部队最多需要多少时间才能全部撤离独木桥。
输入格式
第一行共一个整数 L,表示独木桥的长度。桥上的坐标为 1,2,⋯ L。
第二行共一个整数 N,表示初始时留在桥上的士兵数目。
第三行共有 N 个整数,分别表示每个士兵的初始坐标。
输出格式
共一行,输出 2 个整数,分别表示部队撤离独木桥的最小时间和最大时间。2 个整数由一个空格符分开。
解题思路:
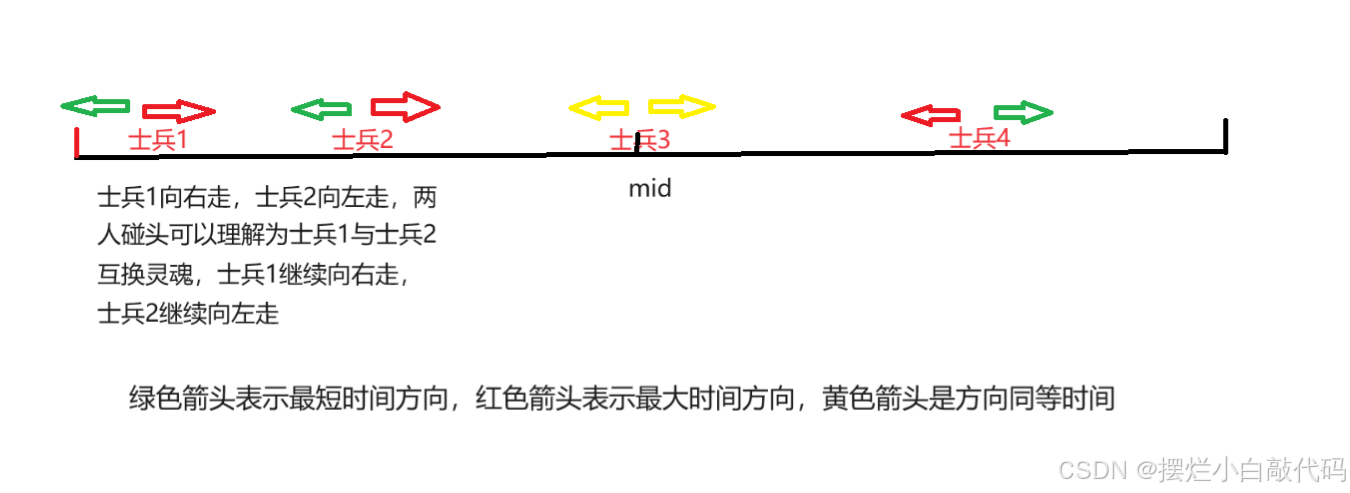
这个题看似显得很累赘,但是做过此类型题的一眼就能看穿,在《挑战程序设计竞赛》这本书上就有详细的解释,当然它们是蚂蚁过桥为背景。解这题的关键在于最大值的求解,我们知道最小值就是在独木桥两边的士兵直接往两端走就可以,走左边还是右边min一下,因为要求所有部队通过所以在所有值里面去一个最大值。对于最大时间的求解,那么我就让靠近左边的人往右边走,靠经右边的人往左边走,如果两个人碰头时,它们可以交换灵魂继续前进,这是《挑战程序设计竞赛》上思想,意思就是我变成他继续前进,他变成我继续前进,最后是对结果没有影响的。那么最大时间就是在最大值里面取一个最大值。
综上所述,最小时间是最小值里面的最大值,最大时间是最大值里面的最大值。
AC代码:
#include<iostream>
#include<algorithm>
using namespace std;
const int N=5e3+5;
int n,l,x;
int a[N];
int main(){
cin>>l>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
sort(a,a+n);//先排序
int minx=0;
int maxx=0;
for(int i=0;i<n;i++){
minx=max(min(a[i],l+1-a[i]),minx);//最小时间
maxx=max(maxx,max(a[i],l+1-a[i]));//最大时间
}
cout<<minx<<" "<<maxx<<endl;
return 0;
}例题三:
AcWing 507. 积木大赛
题目:
春春幼儿园举办了一年一度的“积木大赛”。
今年比赛的内容是搭建一座宽度为 n 的大厦,大厦可以看成由 n 块宽度为 1 的积木组成,第 i 块积木的最终高度需要是 hi。
在搭建开始之前,没有任何积木(可以看成块高度为 0 的积木)。
接下来每次操作,小朋友们可以选择一段连续区间 [L,R],然后将第 L 块到第 R 块之间(含第 L 块和第 R 块)所有积木的高度分别增加 1。
小 M 是个聪明的小朋友,她很快想出了建造大厦的最佳策略,使得建造所需的操作次数最少。
但她不是一个勤于动手的孩子,所以想请你帮忙实现这个策略,并求出最少的操作次数。
输入格式
输入包含两行,第一行包含一个整数 n,表示大厦的宽度。
第二行包含 n 个整数,第 i 个整数为 hi。
输出格式
仅一行,即建造所需的最少操作数。
数据范围
1≤n≤105,
0≤hi≤10000
输入样例:
5
2 3 4 1 2
输出样例:
5
解题思路:
这可不是一道纯正的贪心,因为读完题就知道是差分了,但是为什么还要归到贪心里面,因为贪心是一种思想,上面三个题目都涉及到了最大、最小,一般这种就有贪心思想了,当然,这一个题,会了差分就迎刃而解了,具体的贪心还是体现在算法操作上,比如这个题中间的数最大,那么每次选择区间加一都尽量选上这个数,这样可以使操作次数最小。
AC代码:
#include<iostream>
using namespace std;
int n,ans;
const int N=1e5+5;
int h[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>h[i];
}
for(int i=n+1;i>=1;i--){
h[i]=h[i]-h[i-1];//差分数组
}
for(int i=1;i<=n+1;i++){
if(h[i]>0){
ans+=h[i];
}
}
cout<<ans<<endl;
return 0;
}其他例题:
第十四届蓝桥杯省赛大学C组(C/C++)三国游戏_c语言三国游戏-CSDN博客
AcWing 1262. 鱼塘钓鱼(每日一题)-CSDN博客