第5关:基尼系数
基尼系数
在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益率来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。能不能简化模型同时也不至于完全丢失熵模型的优点呢?当然有!那就是基尼系数!
CART算法使用基尼系数来代替信息增益率,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益与信息增益率是相反的(它们都是越大越好)。
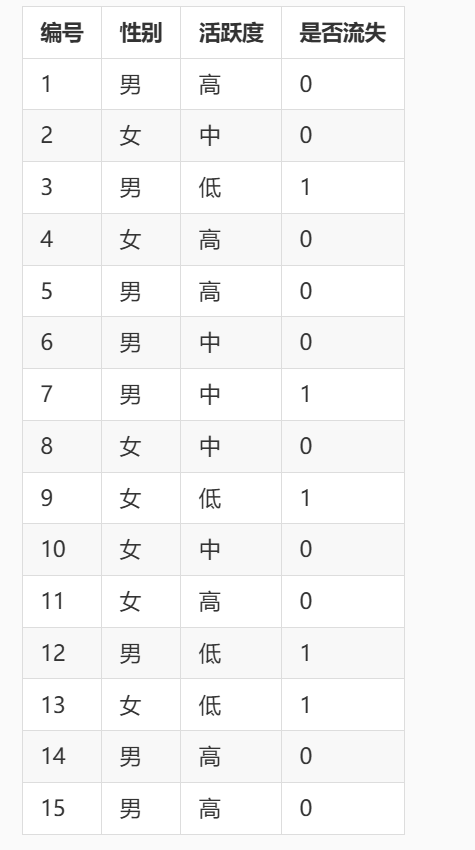
从公式可以看出,相比于信息增益和信息增益率,计算起来更加简单。举个例子,还是使用第二关中提到过的数据集,第一列是编号,第二列是性别,第三列是活跃度,第四列是客户是否流失的标签(0表示未流失,1表示流失)。
代码
import numpy as np
def calcGini(feature, label, index):
'''
计算基尼系数
:param feature:测试用例中字典里的feature,类型为ndarray
:param label:测试用例中字典里的label,类型为ndarray
:param index:测试用例中字典里的index,即feature部分特征列的索引。该索引指的是feature中第几个特征,如index:0表示使用第一个特征来计算信息增益。
:return:基尼系数,类型float
'''
# 计算子集的基尼指数
def calcGiniIndex(label_subset):
total = len(label_subset)
if total == 0:
return 0
label_counts = np.bincount(label_subset)
probabilities = label_counts / total
gini = 1.0 - np.sum(np.square(probabilities))
return gini
# 将feature和label转为numpy数组
f = np.array(feature)
l = np.array(label)
# 得到指定特征列的值的集合
unique_values = np.unique(f[:, index])
total_gini = 0
total_samples = len(label)
# 按照特征的每个唯一值划分数据集
for value in unique_values:
# 获取该特征值对应的样本索引
subset_indices = np.where(f[:, index] == value)[0]
# 获取对应的子集标签
subset_label = l[subset_indices]
# 计算子集的基尼指数
subset_gini = calcGiniIndex(subset_label)
# 加权计算总的基尼系数
weighted_gini = (len(subset_label) / total_samples) * subset_gini
total_gini += weighted_gini
return total_gini
第6关:预剪枝与后剪枝
为什么需要剪枝
决策树的生成是递归地去构建决策树,直到不能继续下去为止。这样产生的树往往对训练数据有很高的分类准确率,但对未知的测试数据进行预测就没有那么准确了,也就是所谓的过拟合。
决策树容易过拟合的原因是在构建决策树的过程时会过多地考虑如何提高对训练集中的数据的分类准确率,从而会构建出非常复杂的决策树(树的宽度和深度都比较大)。在之前的实训中已经提到过,模型的复杂度越高,模型就越容易出现过拟合的现象。所以简化决策树的复杂度能够有效地缓解过拟合现象,而简化决策树最常用的方法就是剪枝。剪枝分为预剪枝与后剪枝。
预剪枝
预剪枝的核心思想是在决策树生成过程中,对每个结点在划分前先进行一个评估,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶结点。
想要评估决策树算法的泛化性能如何,方法很简单。可以将训练数据集中随机取出一部分作为验证数据集,然后在用训练数据集对每个结点进行划分之前用当前状态的决策树计算出在验证数据集上的正确率。正确率越高说明决策树的泛化性能越好,如果在划分结点的时候发现泛化性能有所下降或者没有提升时,说明应该停止划分,并用投票计数的方式将当前结点标记成叶子结点。
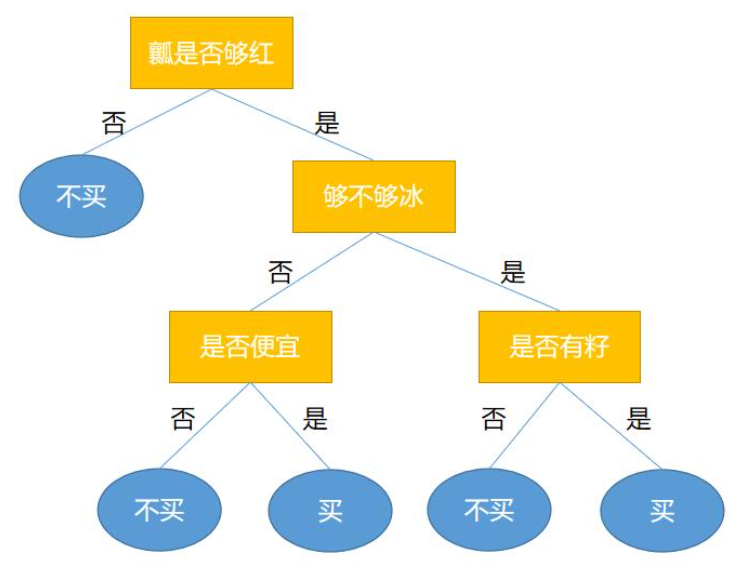
举个例子,假如上一关中所提到的用来决定是否买西瓜的决策树模型已经出现过拟合的情况,模型如下:
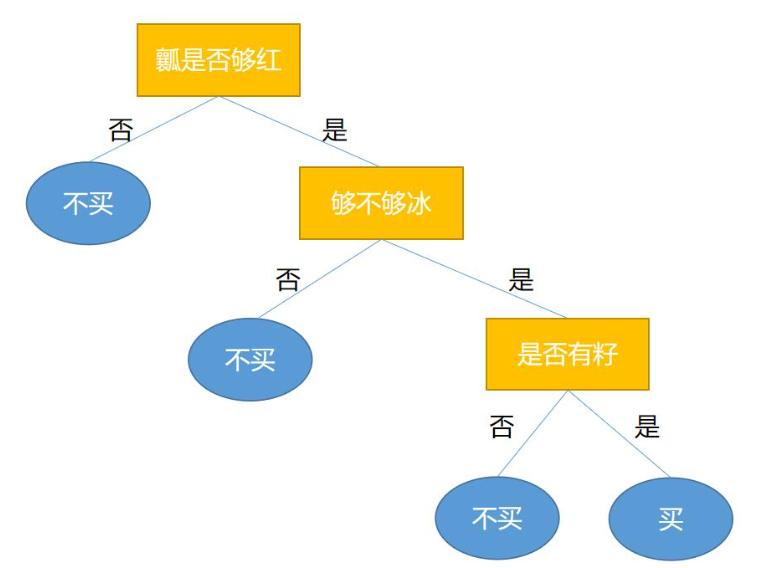
假设当模型在划分是否便宜这个结点前,模型在验证数据集上的正确率为0.81。但在划分后,模型在验证数据集上的正确率降为0.67。此时就不应该划分是否便宜这个结点。所以预剪枝后的模型如下:
从上图可以看出,预剪枝能够降低决策树的复杂度。这种预剪枝处理属于贪心思想,但是贪心有一定的缺陷,就是可能当前划分会降低泛化性能,但在其基础上进行的后续划分却有可能导致性能显著提高。所以有可能会导致决策树出现欠拟合的情况。
后剪枝
后剪枝是先从训练集生成一棵完整的决策树,然后自底向上地对非叶结点进行考察,若将该结点对应的子树替换为叶结点能够带来决策树泛化性能提升,则将该子树替换为叶结点。
后剪枝的思路很直接,对于决策树中的每一个非叶子结点的子树,我们尝试着把它替换成一个叶子结点,该叶子结点的类别我们用子树所覆盖训练样本中存在最多的那个类来代替,这样就产生了一个简化决策树,然后比较这两个决策树在测试数据集中的表现,如果简化决策树在验证数据集中的准确率有所提高,那么该子树就可以替换成叶子结点。该算法以bottom-up的方式遍历所有的子树,直至没有任何子树可以替换使得测试数据集的表现得以改进时,算法就可以终止。
从后剪枝的流程可以看出,后剪枝是从全局的角度来看待要不要剪枝,所以造成欠拟合现象的可能性比较小。但由于后剪枝需要先生成完整的决策树,然后再剪枝,所以后剪枝的训练时间开销更高。
代码
import numpy as np
from copy import deepcopy
class DecisionTree(object):
def __init__(self):
# 决策树模型
self.tree = {}
def calcInfoGain(self, feature, label, index):
# 计算信息增益的代码
def calcInfoEntropy(feature, label):
# 计算信息熵
label_set = set(label)
result = 0
for l in label_set:
count = 0
for j in range(len(label)):
if label[j] == l:
count += 1
p = count / len(label)
result -= p * np.log2(p)
return result
def calcHDA(feature, label, index, value):
# 计算条件熵
count = 0
sub_feature = []
sub_label = []
for i in range(len(feature)):
if feature[i][index] == value:
count += 1
sub_feature.append(feature[i])
sub_label.append(label[i])
pHA = count / len(feature)
e = calcInfoEntropy(sub_feature, sub_label)
return pHA * e
base_e = calcInfoEntropy(feature, label)
f = np.array(feature)
f_set = set(f[:, index])
sum_HDA = 0
for value in f_set:
sum_HDA += calcHDA(feature, label, index, value)
return base_e - sum_HDA
def getBestFeature(self, feature, label):
max_infogain = 0
best_feature = 0
for i in range(len(feature[0])):
infogain = self.calcInfoGain(feature, label, i)
if infogain > max_infogain:
max_infogain = infogain
best_feature = i
return best_feature
def calc_acc_val(self, the_tree, val_feature, val_label):
# 计算验证集准确率
result = []
def classify(tree, feature):
if not isinstance(tree, dict):
return tree
t_index, t_value = list(tree.items())[0]
f_value = feature[t_index]
if isinstance(t_value, dict):
classLabel = classify(tree[t_index][f_value], feature)
return classLabel
else:
return t_value
for f in val_feature:
result.append(classify(the_tree, f))
result = np.array(result)
return np.mean(result == val_label)
def createTree(self, train_feature, train_label):
# 创建决策树
if len(set(train_label)) == 1:
return train_label[0]
if len(train_feature[0]) == 1 or len(np.unique(train_feature, axis=0)) == 1:
vote = {}
for l in train_label:
if l in vote.keys():
vote[l] += 1
else:
vote[l] = 1
max_count = 0
vote_label = None
for k, v in vote.items():
if v > max_count:
max_count = v
vote_label = k
return vote_label
best_feature = self.getBestFeature(train_feature, train_label)
tree = {best_feature: {}}
f = np.array(train_feature)
f_set = set(f[:, best_feature])
for v in f_set:
sub_feature = []
sub_label = []
for i in range(len(train_feature)):
if train_feature[i][best_feature] == v:
sub_feature.append(train_feature[i])
sub_label.append(train_label[i])
tree[best_feature][v] = self.createTree(sub_feature, sub_label)
return tree
def post_cut(self, val_feature, val_label):
# 剪枝相关代码
def get_non_leaf_node_count(tree):
non_leaf_node_path = []
def dfs(tree, path, all_path):
for k in tree.keys():
if isinstance(tree[k], dict):
path.append(k)
dfs(tree[k], path, all_path)
if len(path) > 0:
path.pop()
else:
all_path.append(path[:])
dfs(tree, [], non_leaf_node_path)
unique_non_leaf_node = []
for path in non_leaf_node_path:
isFind = False
for p in unique_non_leaf_node:
if path == p:
isFind = True
break
if not isFind:
unique_non_leaf_node.append(path)
return len(unique_non_leaf_node)
def get_the_most_deep_path(tree):
non_leaf_node_path = []
def dfs(tree, path, all_path):
for k in tree.keys():
if isinstance(tree[k], dict):
path.append(k)
dfs(tree[k], path, all_path)
if len(path) > 0:
path.pop()
else:
all_path.append(path[:])
dfs(tree, [], non_leaf_node_path)
max_depth = 0
result = None
for path in non_leaf_node_path:
if len(path) > max_depth:
max_depth = len(path)
result = path
return result
def set_vote_label(tree, path, label):
for i in range(len(path)-1):
tree = tree[path[i]]
tree[path[len(path)-1]] = label
acc_before_cut = self.calc_acc_val(self.tree, val_feature, val_label)
for _ in range(get_non_leaf_node_count(self.tree)):
path = get_the_most_deep_path(self.tree)
tree = deepcopy(self.tree)
step = deepcopy(tree)
for k in path:
step = step[k]
vote_label = sorted(step.items(), key=lambda item: item[1], reverse=True)[0][0]
set_vote_label(tree, path, vote_label)
acc_after_cut = self.calc_acc_val(tree, val_feature, val_label)
if acc_after_cut > acc_before_cut:
set_vote_label(self.tree, path, vote_label)
acc_before_cut = acc_after_cut
def fit(self, train_feature, train_label, val_feature, val_label):
# 训练决策树模型
self.tree = self.createTree(train_feature, train_label)
self.post_cut(val_feature, val_label)
def predict(self, feature):
# 预测函数
result = []
def classify(tree, feature):
if not isinstance(tree, dict):
return tree
t_index, t_value = list(tree.items())[0]
f_value = feature[t_index]
if isinstance(t_value, dict):
classLabel = classify(tree[t_index][f_value], feature)
return classLabel
else:
return t_value
for f in feature:
result.append(classify(self.tree, f))
return np.array(result)
第7关:鸢尾花识别
掌握如何使用sklearn提供的DecisionTreeClassifier
数据简介:
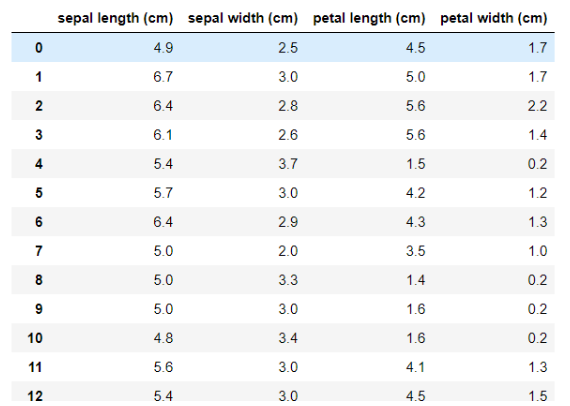
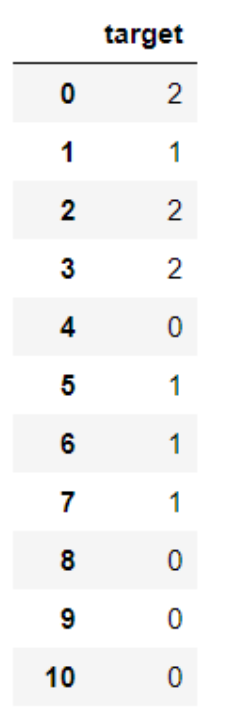
鸢尾花数据集是一类多重变量分析的数据集。通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类(其中分别用0,1,2代替)。
数据集中部分数据与标签如下图所示:
DecisionTreeClassifier
DecisionTreeClassifier的构造函数中有两个常用的参数可以设置:
criterion:划分节点时用到的指标。有gini(基尼系数),entropy(信息增益)。若不设置,默认为gini
max_depth:决策树的最大深度,如果发现模型已经出现过拟合,可以尝试将该参数调小。若不设置,默认为None
和sklearn中其他分类器一样,DecisionTreeClassifier类中的fit函数用于训练模型,fit函数有两个向量输入:
X:大小为[样本数量,特征数量]的ndarray,存放训练样本;
Y:值为整型,大小为[样本数量]的ndarray,存放训练样本的分类标签。
DecisionTreeClassifier类中的predict函数用于预测,返回预测标签,predict函数有一个向量输入:
X:大小为[样本数量,特征数量]的ndarray,存放预测样本。
DecisionTreeClassifier的使用代码如下:
from sklearn.tree import DecisionTreeClassifier
clf = tree.DecisionTreeClassifier()
clf.fit(X_train, Y_train)
result = clf.predict(X_test)
代码
#********* Begin *********#
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
train_df = pd.read_csv('./step7/train_data.csv').as_matrix()
train_label = pd.read_csv('./step7/train_label.csv').as_matrix()
test_df = pd.read_csv('./step7/test_data.csv').as_matrix()
dt = DecisionTreeClassifier()
dt.fit(train_df, train_label)
result = dt.predict(test_df)
result = pd.DataFrame({'target':result})
result.to_csv('./step7/predict.csv', index=False)
#********* End *********#