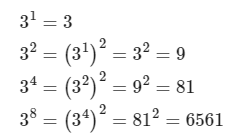前言：

幂运算是一种常见的运算，求取a^n,最容易想到的方法便是通过循环逐个累乘，其复杂度为O(n)，这在很多时候是不够快的，所以我们需要一种算法来优化幂运算的过程。

快速幂，二进制取幂（Binary Exponentiation，也称平方法），是一个在O(logn)的时间内计算a^n的小技巧。

解释：

如下计算公式，无需多言

那么计算一个数的n次幂的时候，就可以将n转化为二进制数，比如计算

因此，计算3^13，只要将对应的二进制位为1的整数幂 乘起来就行了

实现

经过以上的介绍，快速幂的代码实现就比较容易了：

// 计算x 的 n 次幂
public static double fastPow(int x, int n) {
    // 0的任何次幂都是0
    if (x == 0) {
        return 0;
    }
    // 非0的零次幂是1
    if (n == 0) {
        return 1;
    }
    // 负数次幂计算
    if (n < 0) {
        x = 1 / x;
        n = -n;
    }

    double res = 1.0;
    while (n > 0) {
        // 当前n的最低位不是0，最终结果就要乘以这个值
        if ((n & 1) == 1) {
            res *= x;
        }

        // 从低到高位进行运算，低位运算完了，就要到高一位了
        n = n >> 1;
        // 高一位的值，也就是计算结果要乘以的值。
        x *= x;
    }
    return res;
}

实战

1969. 数组元素的最小非零乘积

思路：

1、首先假设给定三个正整数 a,b,,c，满足 a<b<c，此时需要将某个数缩小 1，另外一个数增加 1，使得 abc 最小，如何选择才是最优选择？---> 最优解其实就是大数加1，小数减1。即(a-1)b(c+1)。

2、回到本题，两个数在进行相同的位交换的时候，本质就是将一个数减小2^k，另外一个数增大2^k，我们可以知道一种贪心思路：进行相同位交换时，优先缩小数组中最小的元素，再增加数组中最大的元素

    public static int minNonZeroProduct(int p) {
        if (p == 1) {
            return 1;
        }

        // 题目给的取余数
        int mod = 1000000007;
        // 数组最后一个值
        long last = fastPow(2, p, mod) - 1;

        // 需要计算的数目,注意这里不能用快速幂计算，因为用了余数取模，算出来的数目大于模数的时候就不准了
        long binarySize = (long) 1 << (p - 1);
        binarySize = binarySize - 1;

        // 结果
        return (int) (fastPow(last - 1, binarySize, mod) * last % mod);

    }

    public static long fastPow(long x, long n, int mod) {
        long res = 1l;
        while (n > 0) {
            if ((n & 1) == 1) {
                res = res * x % mod;
            }
            n = n >> 1;
            x = x * x % mod;
        }
        return res;
    }