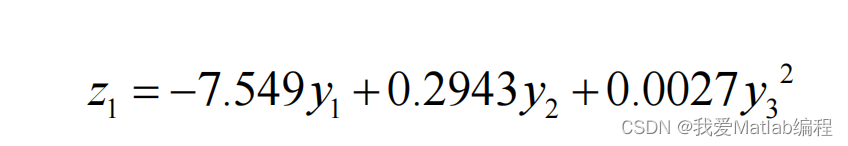【数学建模】多元非线性回归nlinfit（Matlab代码实现）

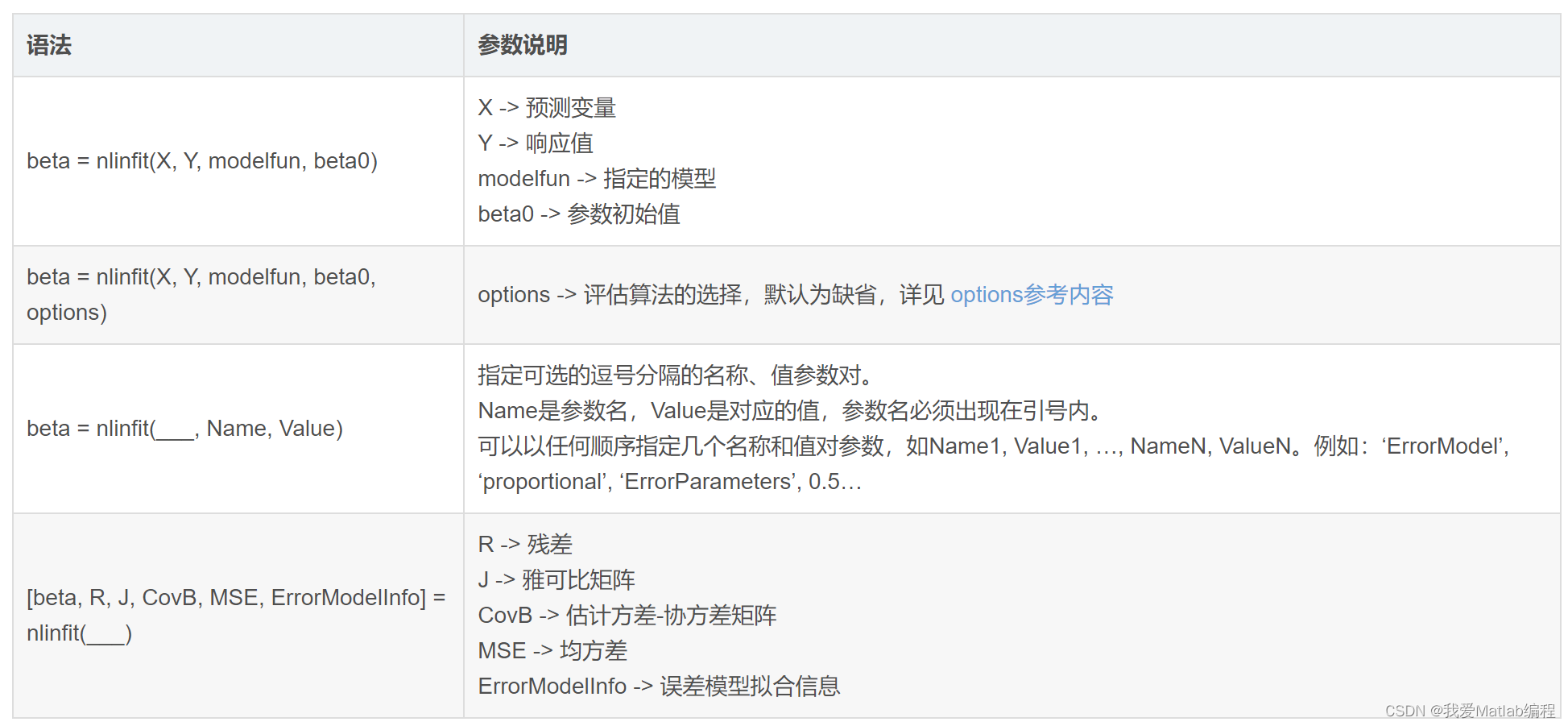
1 基本语法

2 算例及Matlab代码实现

2.1 算例

熔喷非织造材料是口罩生产的重要原材料，具有很好的过滤性能，其生产工艺简单、成本低、质量轻等特点，受到国内外企业的广泛关注。但是，由于熔喷非织造材料纤维非常细，在使用过程中经常因为压缩回弹性差而导致其性能得不到保障。因此，科学家们创造出插层熔喷法，即通过在聚丙烯（PP）熔喷制备过程中将涤纶(PET）短纤等纤维插入熔喷纤维流，制备出了“Z型”结构的插层熔喷非织造材料。
插层熔喷非织造材料制备工艺参数较多，参数之间还存在交互影响，加上插层气流之后更为复杂，因此，通过工艺参数（接收距离和热空气速度）决定结构变量（厚度、孔隙率、压缩回弹性)，而由结构变量决定最终产品性能（过滤阻力、过滤效率、透气性）的研究也变得较为复杂。如果能分别建立工艺参数与结构变量、结构变量和产品性能之间的关系模型，则有助于为产品性能调控机制的建立提供一定的理论基础。请查阅相关文献，了解专业背景，研究题目数据，回答下列问题。

问题:请研究结构变量与产品性能的关系，以及结构变量之间、产品性能之间的关系。

这里以产品性能中过滤阻力与结构变量（厚度、孔隙率、压缩回弹性)的关系。

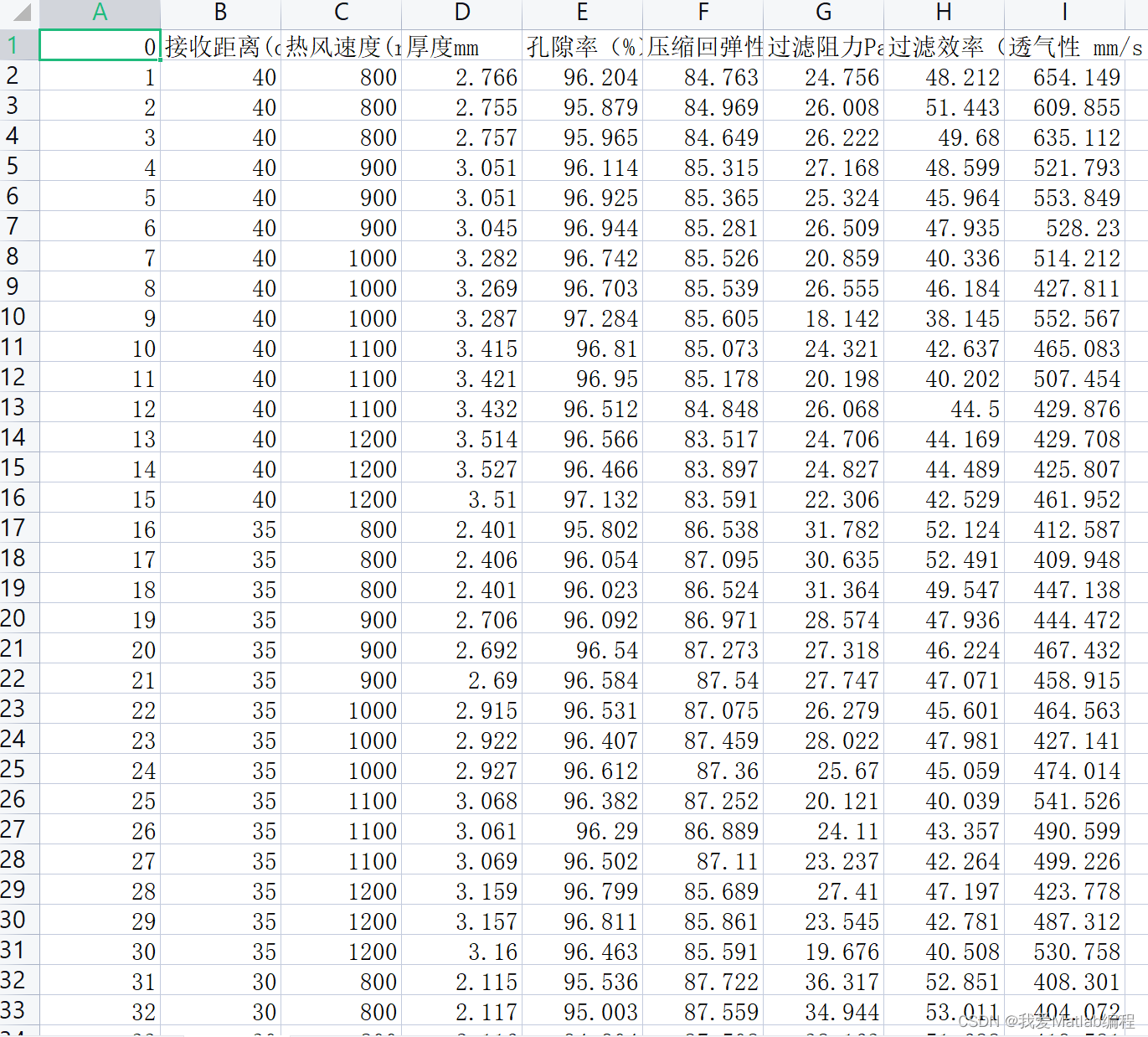
2.2 数据

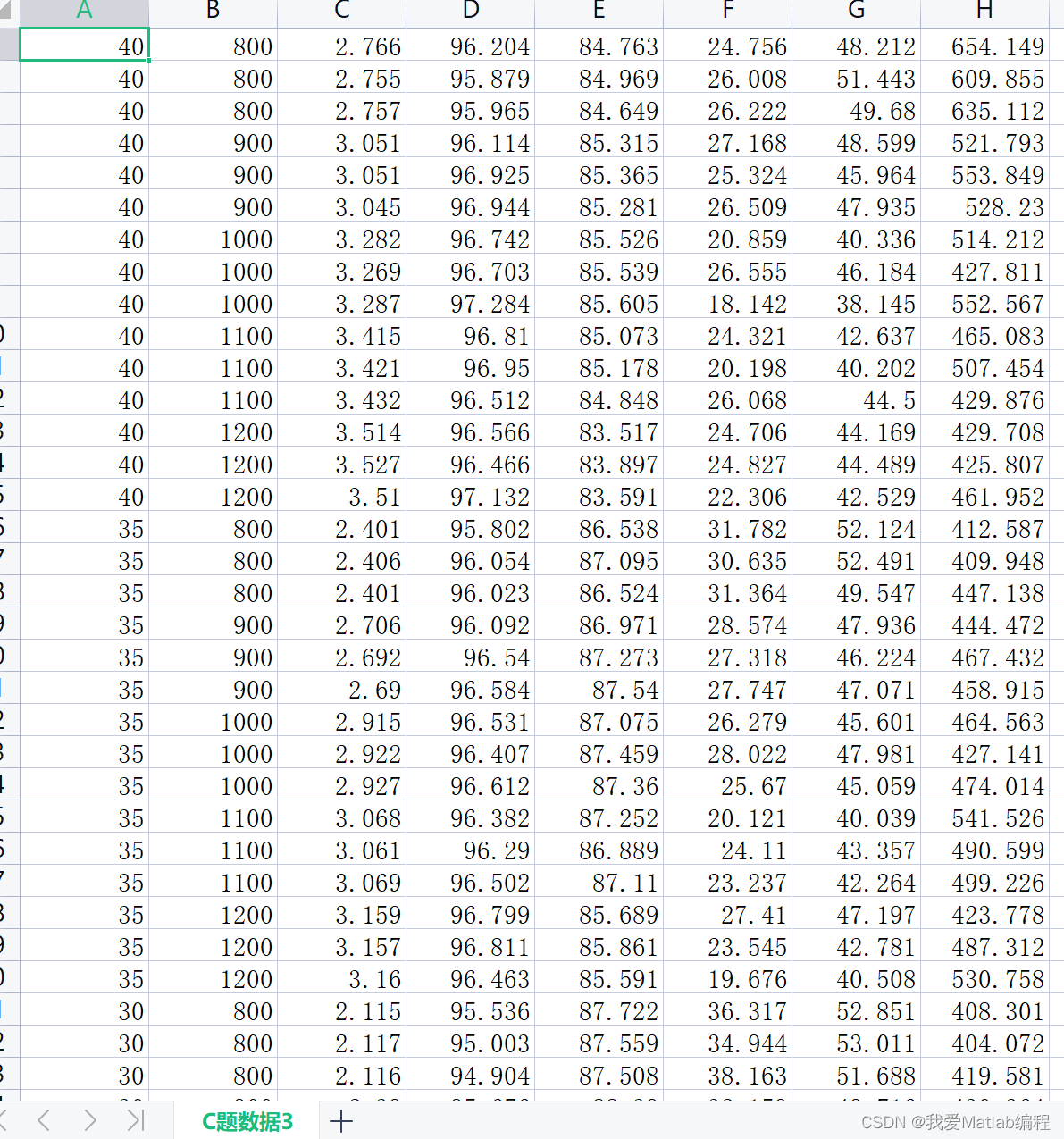
整理一下，方便编程：

2.3 Matlab代码实现

主函数：main

clear
clc
data =csvread('C题数据3.csv')  

x1 = data(:,3);  %厚度mm
x2 = data(:,4);  %孔隙率（%）
x3= data(:,5);  %压缩回弹性率（%）
% x4= data(:,4);
% x5= data(:,5);
% x1=[1.1 1 1.2 1.1 0.9]';
% x2=[2 2 1.8 1.9 2.1]';
% x3=[3.2 3.2 3 2.9 2.9]';
y=data(:,6);  %过滤阻力Pa,
X=[x1,x2,x3];
beta0=[1,1,1];
[beta,r,J,CovB]=nlinfit(X,y,'myfun',beta0);
% 非线性回归
    % beta—系数估计
    % r—残差
    % J—雅可比矩阵
[Ypred,delta]=nlpredci('myfun', X, beta, r, 'Jacobian', J)
%plot(X(:, 1), y, 'k.', X(:, 1), Ypred, 'r');

%% 输出设置
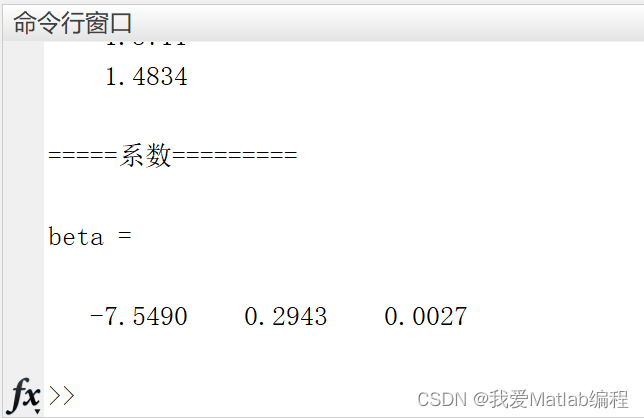
disp('=====系数=========')
beta

子函数：myfun

function y=myfun(beta,x)
y=beta(1)*x(:,1)+beta(2)*x(:,2)+beta(3)*x(:,3).^2;

结果：

全部求解结果：