目录

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

💥1 概述

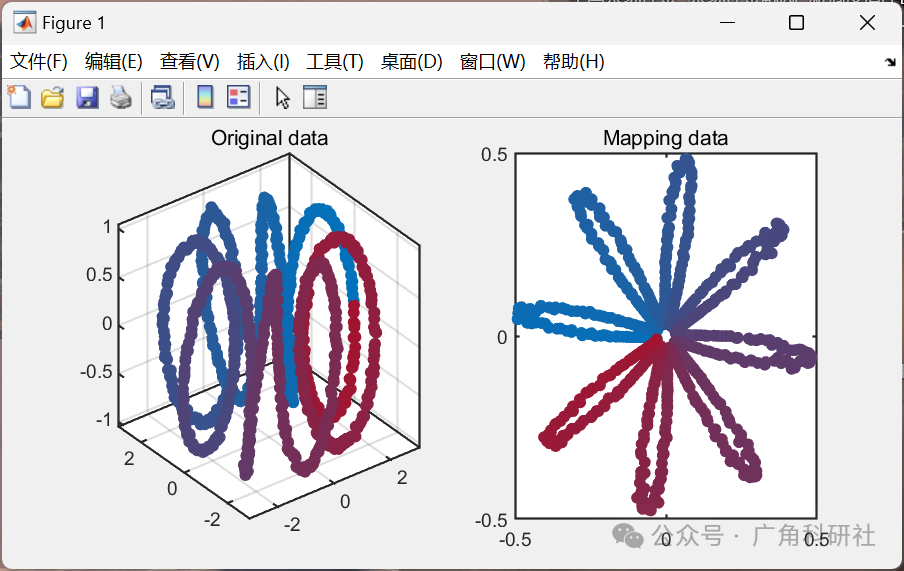
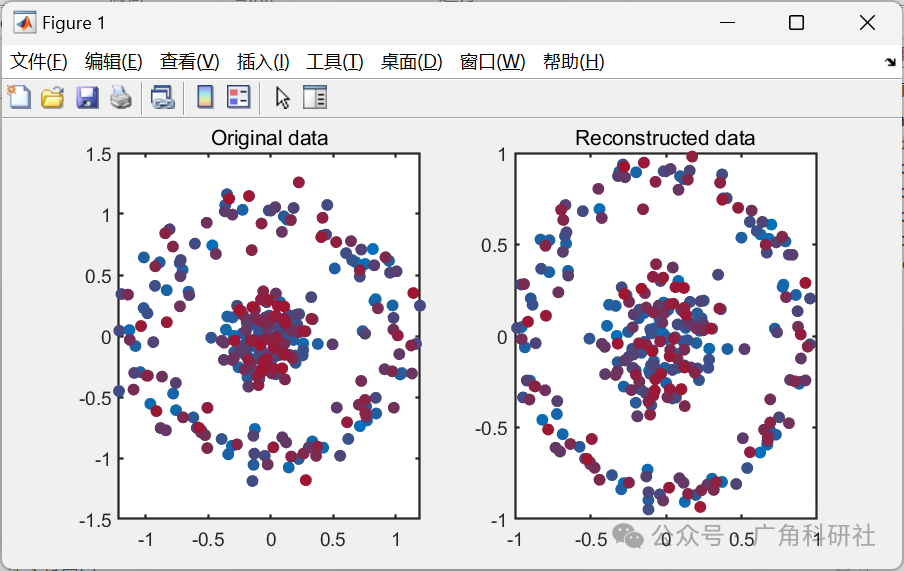
基于核主成分分析（KPCA）进行降维、特征提取、故障检测和故障诊断是一种常见的方法，特别适用于高维数据和非线性特征。通过KPCA，可以将高维数据映射到一个低维的核空间中，从而实现降维。在这个低维空间中，可以更容易地进行特征提取和故障检测，因为数据结构更加清晰。故障诊断则可以利用KPCA映射后的数据，结合适当的分类器或聚类算法来进行。

除了KPCA，还有其他一些常用的降维和特征提取方法，如主成分分析（PCA）、线性判别分析（LDA）、t分布邻域嵌入（t-SNE）等。每种方法都有其适用的场景和特点。例如，PCA适用于线性数据降维，而LDA则适用于分类问题。另外，对于故障检测和诊断，还可以使用支持向量机（SVM）、K均值聚类等算法进行分析和预测。综合考虑数据的性质和任务的需求，选择合适的方法进行处理和分析是非常重要的。

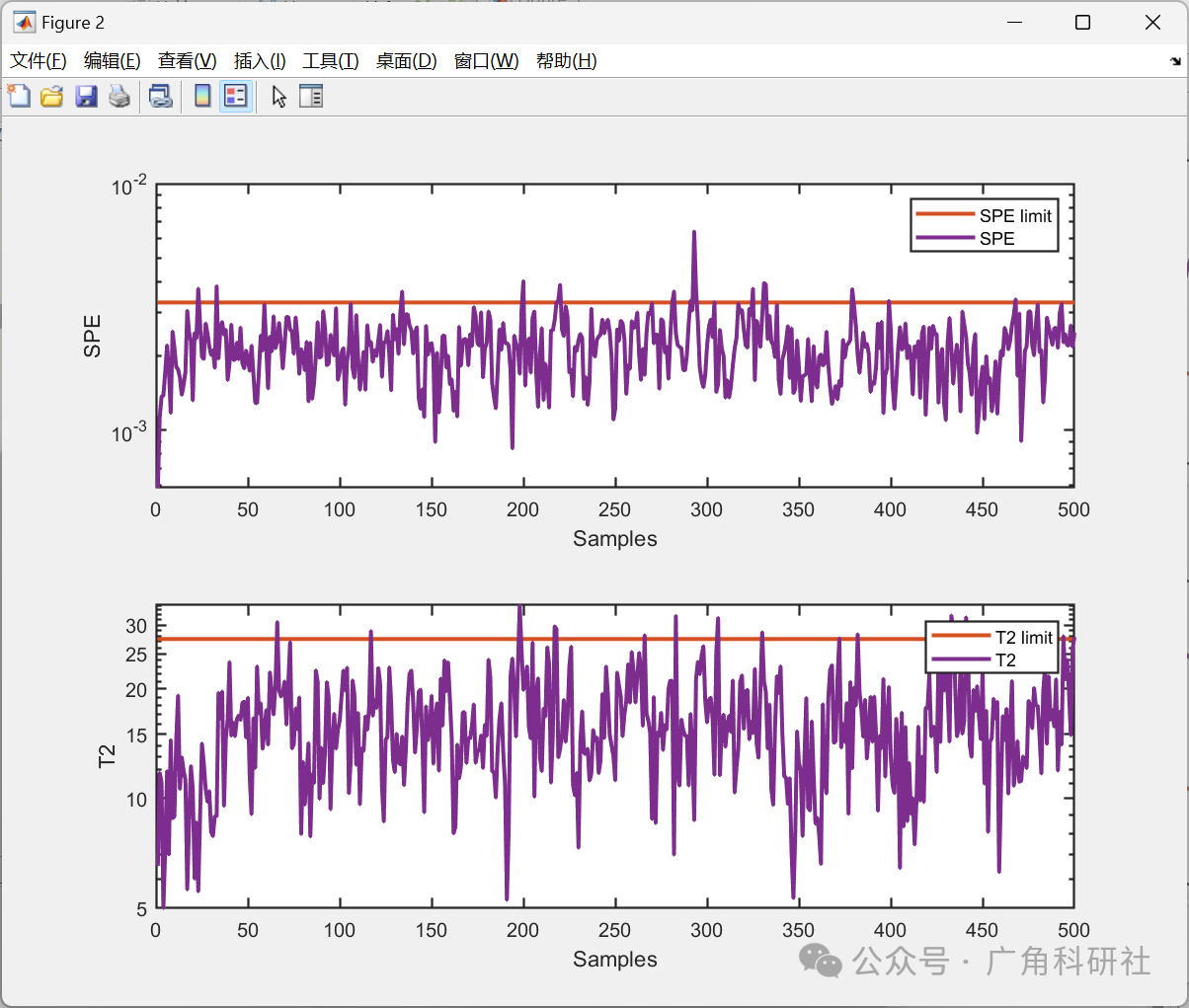
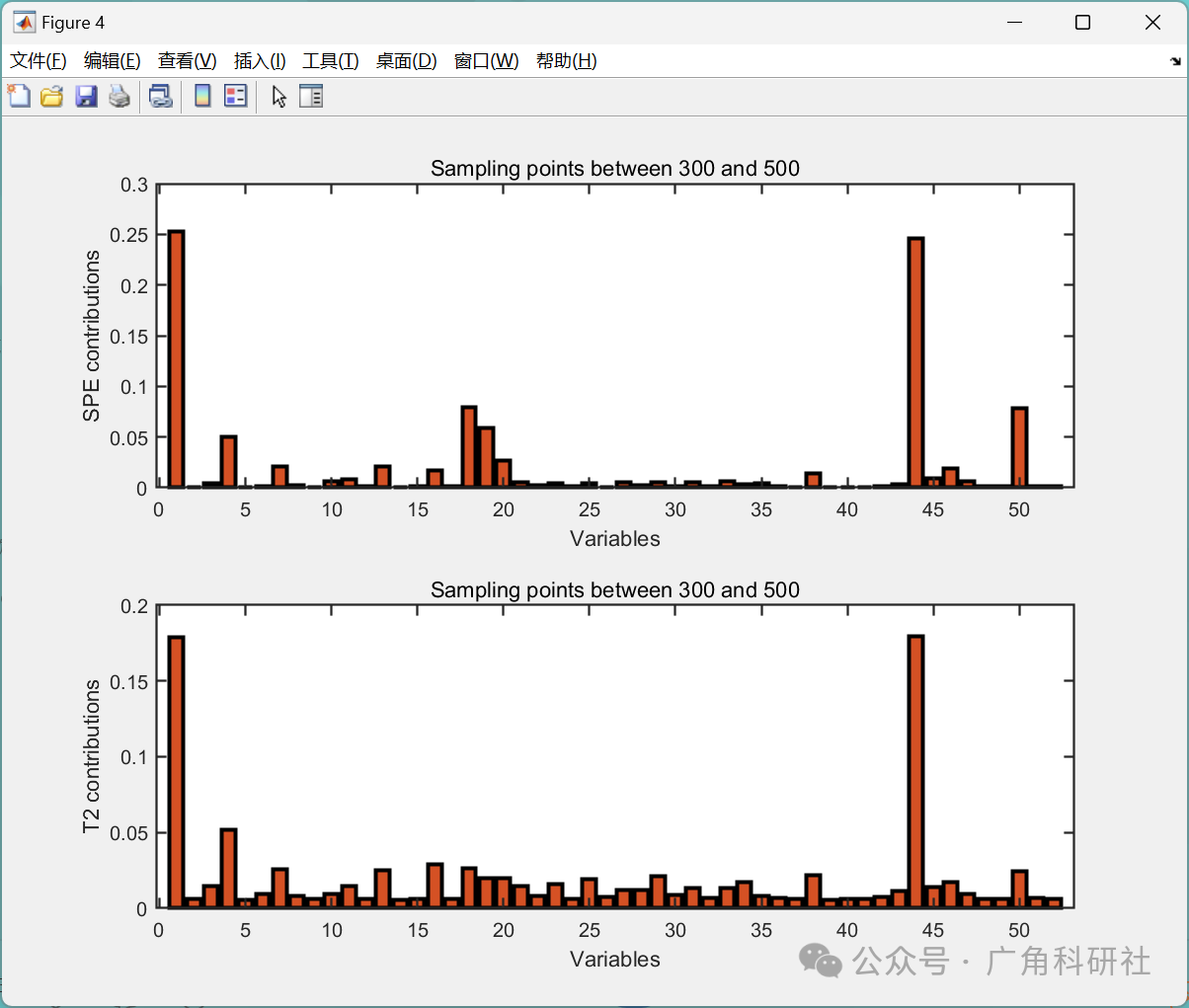
📚2 运行结果

主函数部分代码：

%{
    Demonstration of dimensionality reduction using KPCA.
%}
clc
clear all
close all
addpath(genpath(pwd))
​
load('.\data\TE.mat', 'trainData')
kernel = Kernel('type', 'gaussian', 'gamma', 1/128^2);
​
%% case 1
%{
    The number of components is determined by the given explained level.
    The given explained level should be 0 < explained level < 1.
    For example, when explained level is set to 0.75, the parameter should
    be set as:
​
    parameter = struct('numComponents', 0.75, ...
                       'kernelFunc', kernel);
%}
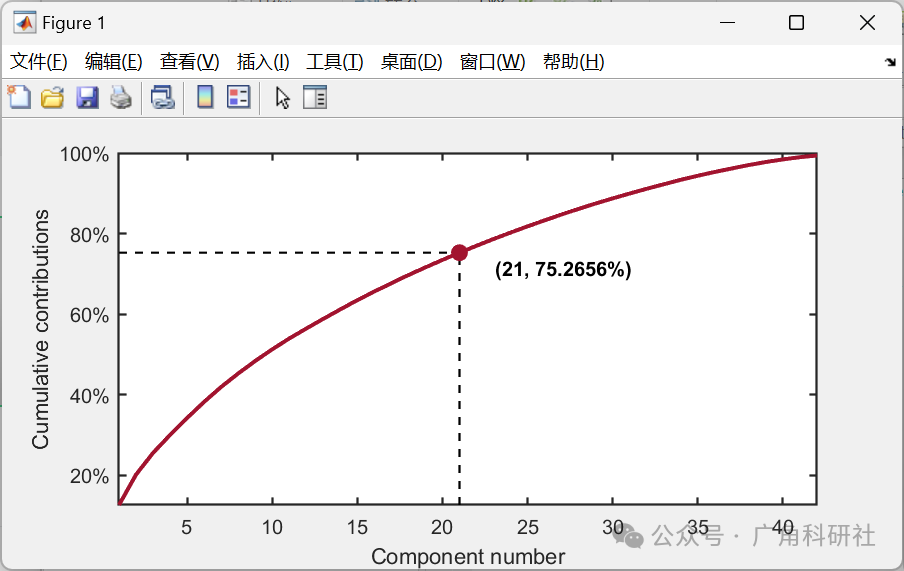
parameter = struct('numComponents', 0.75, ...
                   'kernelFunc', kernel);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(trainData);
​
% Visualization
kplot = KernelPCAVisualization();
kplot.cumContribution(kpca)
​
%% case 2
%{
    The number of components is determined by the given number.
    For example, when the given number is set to 24, the parameter should
    be set as:
​
    parameter = struct('numComponents', 24, ...
                       'kernelFunc', kernel);
%}
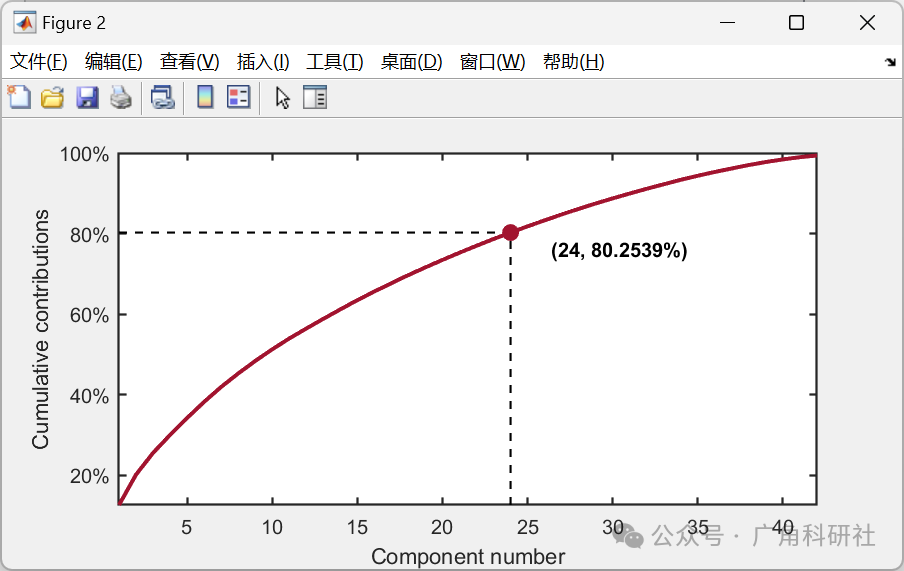
parameter = struct('numComponents', 24, ...
                   'kernelFunc', kernel);
% build a KPCA object
kpca = KernelPCA(parameter);
% train KPCA model
kpca.train(trainData);
​
% Visualization
kplot = KernelPCAVisualization();
kplot.cumContribution(kpca)
​
​

🎉3 参考文献

[1]陈盟.基于核主成分分析和支持向量回归对每日和每分钟股票价格的预测[D].兰州大学,2020.​

部分理论引用网络文献，若有侵权联系博主删除。