💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学,什么是电的时候,不要觉得这些问题搞笑。哲学是科学之母,哲学就是追究终极问题,寻找那些不言自明只有小孩子会问的但是你却回答不出来的问题。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能让人胸中升起一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它居然给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥1 概述
基于EEMD(集合经验模态分解)-MPE(多尺度排列熵)-KPCA(核主元分析)-BiLSTM(双向长短期记忆网络)的故障识别与诊断方法,是一种综合性的信号处理与数据分析技术,能够高效地处理非平稳、非线性信号,并从中提取关键故障特征。以下是该方法的基本步骤及应用优势:
1. 集合经验模态分解(EEMD)
目的:将原始信号分解成一系列本征模态函数(IMF),这些IMF反映了信号在不同频率尺度上的成分,从而去除了噪声,保留了信号的本质特征。
步骤:
- 在原始信号中加入均匀分布的高斯白噪声。
- 对加噪后的信号进行经验模态分解(EMD),得到多个IMF和一个残差分量。
- 重复上述过程多次,并对每次分解得到的IMF取均值,作为最终的EEMD分解结果。
优势:通过引入白噪声,EEMD能够解决EMD方法中的模态混叠问题,使得分解结果更加稳定可靠。
2. 多尺度排列熵(MPE)
目的:评估每个IMF的复杂性和信息量,以便区分噪声IMF、混合IMF和信息IMF。
步骤:
- 对每个IMF计算排列熵值,以量化其复杂性和信息含量。
- 根据排列熵值将IMF分类为噪声IMF、混合IMF和信息IMF。
优势:MPE能够有效地区分信号中的噪声成分和有用信息,为后续处理提供了有力支持。
3. 核主元分析(KPCA)
目的:从处理后的IMF中提取关键故障特征,降低数据维度,提高处理效率。
步骤:
- 将经过MPE筛选的信息IMF和混合IMF作为KPCA的输入。
- 通过非线性映射将原始数据投影到高维特征空间。
- 在高维特征空间中进行主成分分析,提取非线性主成分。
优势:KPCA能够处理非线性数据,有效地提取出影响故障率的关键因子,为后续的诊断提供了有力的数据支持。
4. 双向长短期记忆网络(BiLSTM)
目的:利用BiLSTM对提取出的关键故障特征进行建模,实现故障识别和诊断。
步骤:
- 将KPCA提取出的非线性主成分作为BiLSTM的输入。
- BiLSTM通过前向和后向两个LSTM网络捕捉序列数据中的双向依赖关系。
- 对BiLSTM的输出进行进一步处理,实现故障的分类和识别。
优势:BiLSTM能够充分利用序列数据的前后文信息,提高故障识别的准确性和鲁棒性。
总结
基于EEMD-MPE-KPCA-BiLSTM的故障识别与诊断方法,通过集成多种先进的信号处理和数据分析技术,能够有效地处理非平稳、非线性信号,并从中提取出关键故障特征。该方法在多个领域具有广泛的应用前景,如旋转机械、变压器等设备的故障诊断和预测维护。通过不断优化和改进各个环节的技术实现,可以进一步提高故障识别的准确性和效率。
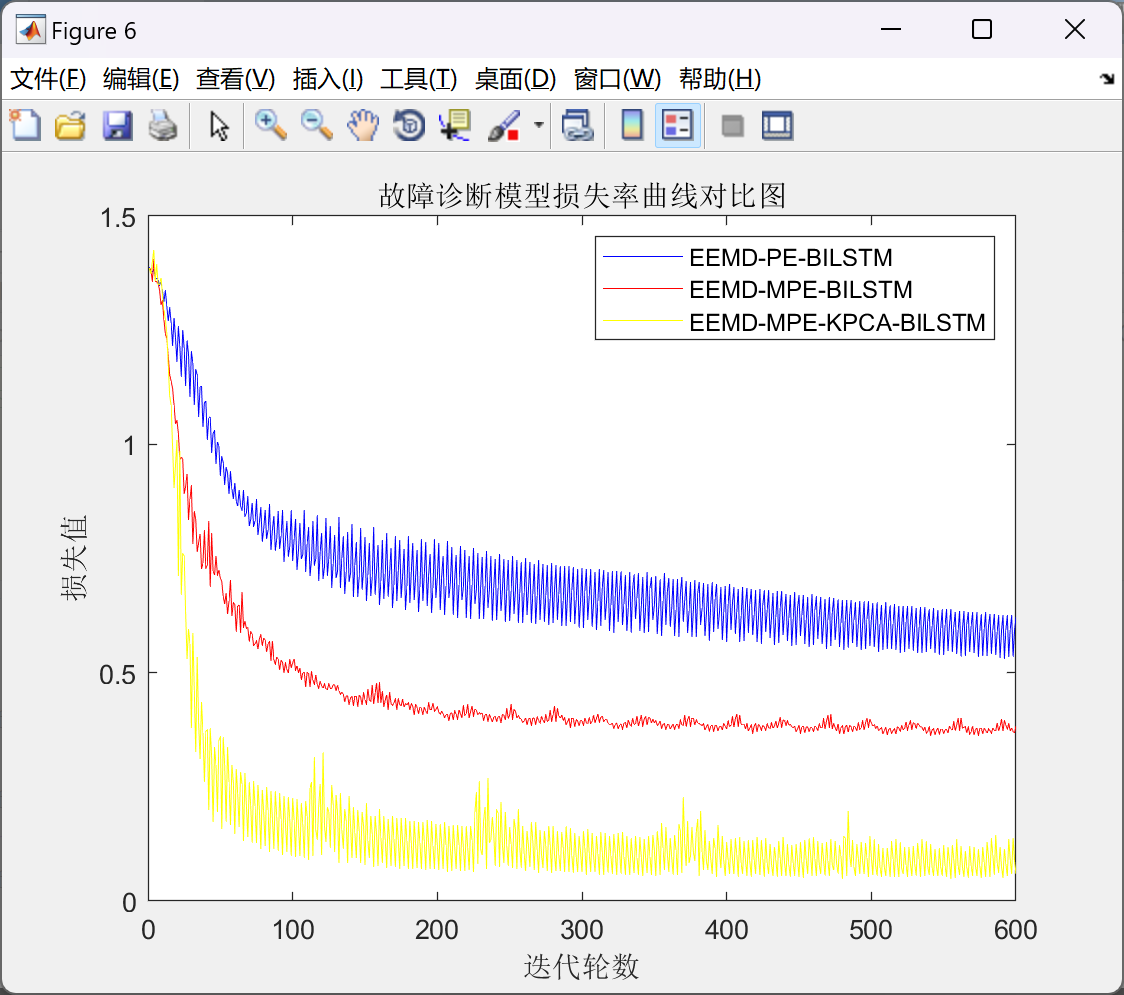
📚2 运行结果
部分代码:
%% EEMD-MPE-PCA-bilstm%% EEMD-MPE-PCA-bilstm%% EEMD-MPE-PCA-bilstm
data3=Y; %读取kpca数据
%输入输出数据
input3=data3(:,1:end-1); %data的第一列-倒数第二列为特征指标
output3=data3(:,end); %data的最后面一列为标签类型
N=length(output3); %全部样本数目
testNum=0.2*N; %设定测试样本数目
trainNum=N-testNum; %计算训练样本数目
%训练集、测试集
P_train3 = input3(1:trainNum,:)';
T_train3 =output3(1:trainNum)';
P_test3 =input3(trainNum+1:trainNum+testNum,:)';
T_test3 =output3(trainNum+1:trainNum+testNum)';
num_class = length(unique(data3(:, end))); % 类别数(Excel最后一列放类别)
t_train3 = categorical(T_train3)';
t_test3 = categorical(T_test3 )';
% 数据归一化
[p_train3, ps_input] = mapminmax(P_train3, 0, 1);
p_test3 = mapminmax('apply', P_test3, ps_input );
% 格式转换
for i = 1 : trainNum
pp_train3{i, 1} = p_train3(:, i);
end
for i = 1 : testNum
pp_test3{i, 1} = p_test3(:, i);
end
% 创建网络
numFeatures = size(P_train3, 1); % 特征维度
numResponses = num_class;
layers = [ ...
sequenceInputLayer(numFeatures) % 输入层
bilstmLayer(120, 'OutputMode', 'last') % bilstm层
reluLayer % Relu 激活层
fullyConnectedLayer(numResponses) % 全连接层数等于分类数
softmaxLayer % 损失函数层
classificationLayer]; % 分类层
% 参数设置
checkpointPath = pwd;
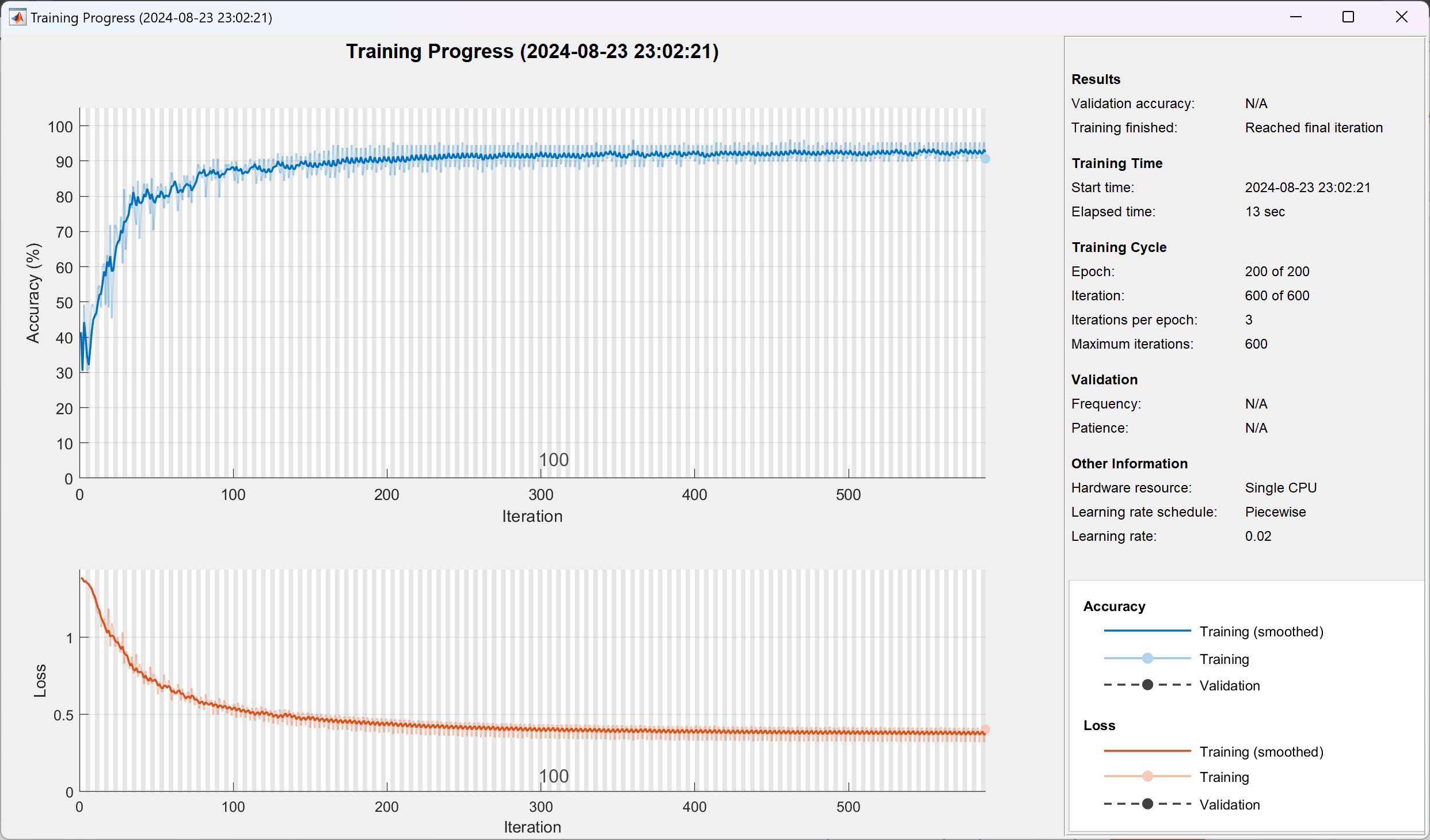
options = trainingOptions('adam', ... % 优化算法Adam
'MaxEpochs', 200, ... % 最大训练次数
'GradientThreshold', 1, ... % 梯度阈值
'InitialLearnRate', 0.045, ... % 初始学习率
'LearnRateSchedule', 'piecewise', ... % 学习率调整
'LearnRateDropPeriod', 200, ... % 训练700次后开始调整学习率
'L2Regularization', 0.001, ... % 正则化参数
'LearnRateDropFactor',0.2, ... % 学习率调整因子
'ExecutionEnvironment', 'cpu',... % 训练环境
'Verbose', 0, ... % 关闭优化过程
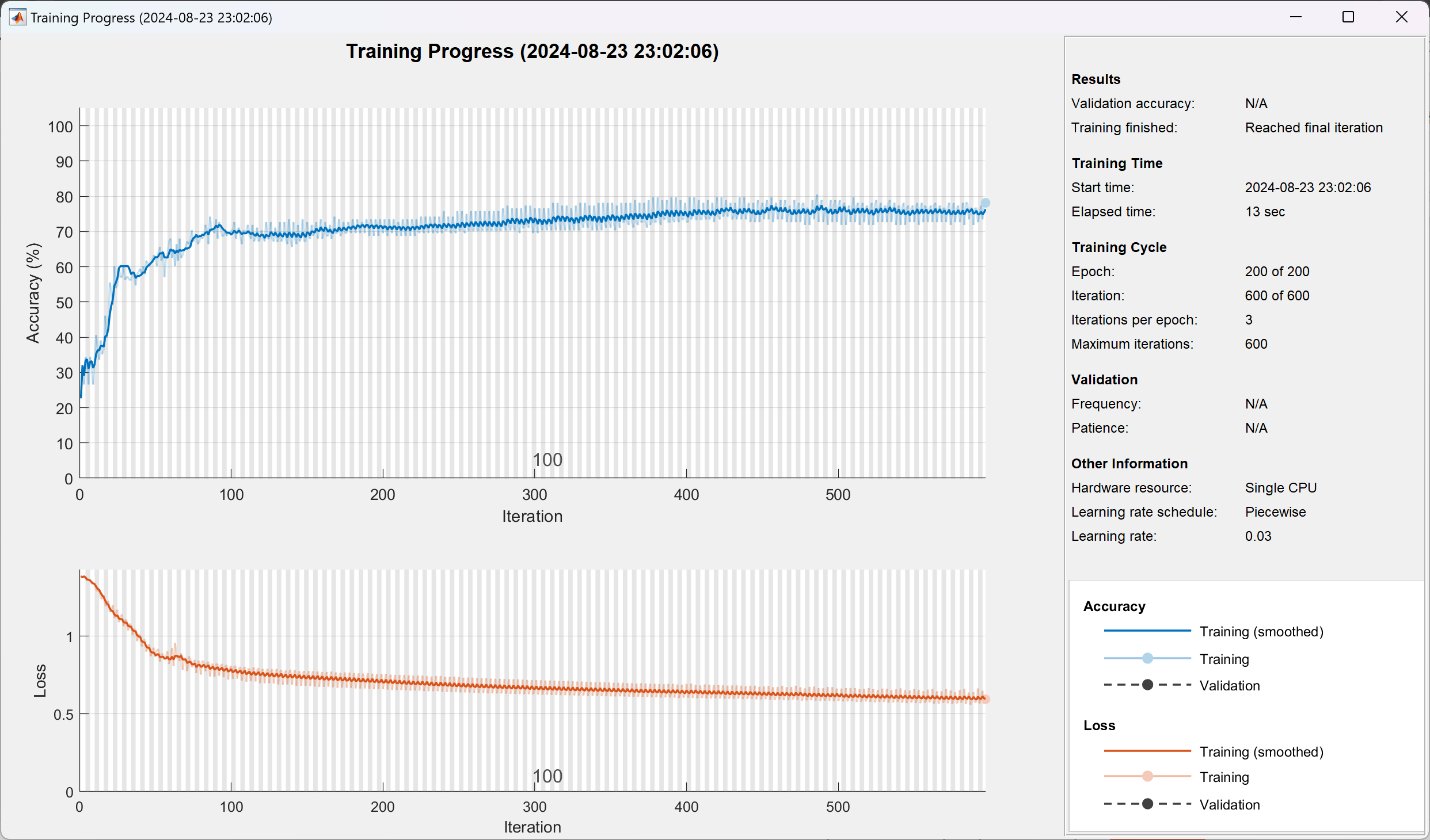
'Plots', 'training-progress'); % 画出曲线
% 训练
[net_MSE2,info3] = trainNetwork(pp_train3, t_train3, layers, options);
% 预测
t_sim1_MSE = classify(net_MSE2, pp_train3);
t_sim2_MSE = classify(net_MSE2, pp_test3);
% 反归一化
T_sim1_MSE = double(t_sim1_MSE');
T_sim2_MSE = double(t_sim2_MSE');
disp('-------------------------------------------------------------')
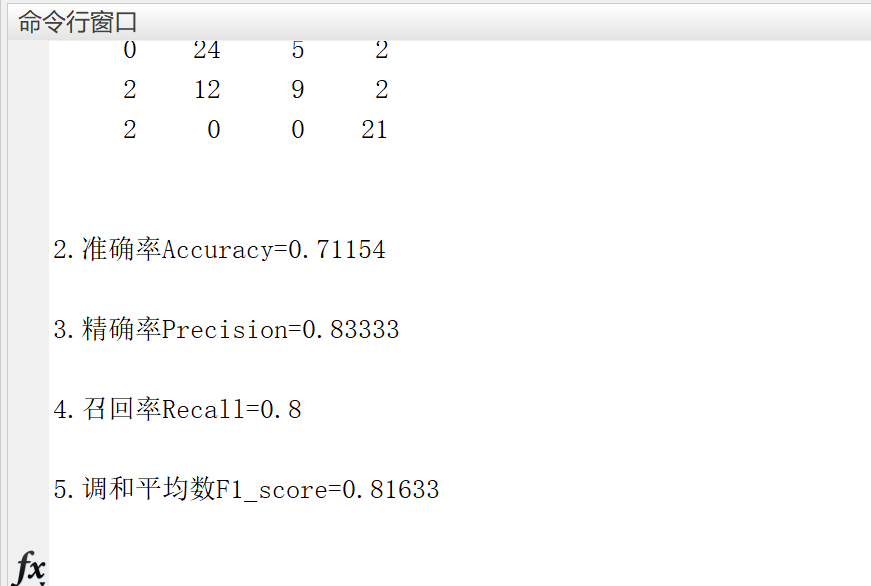
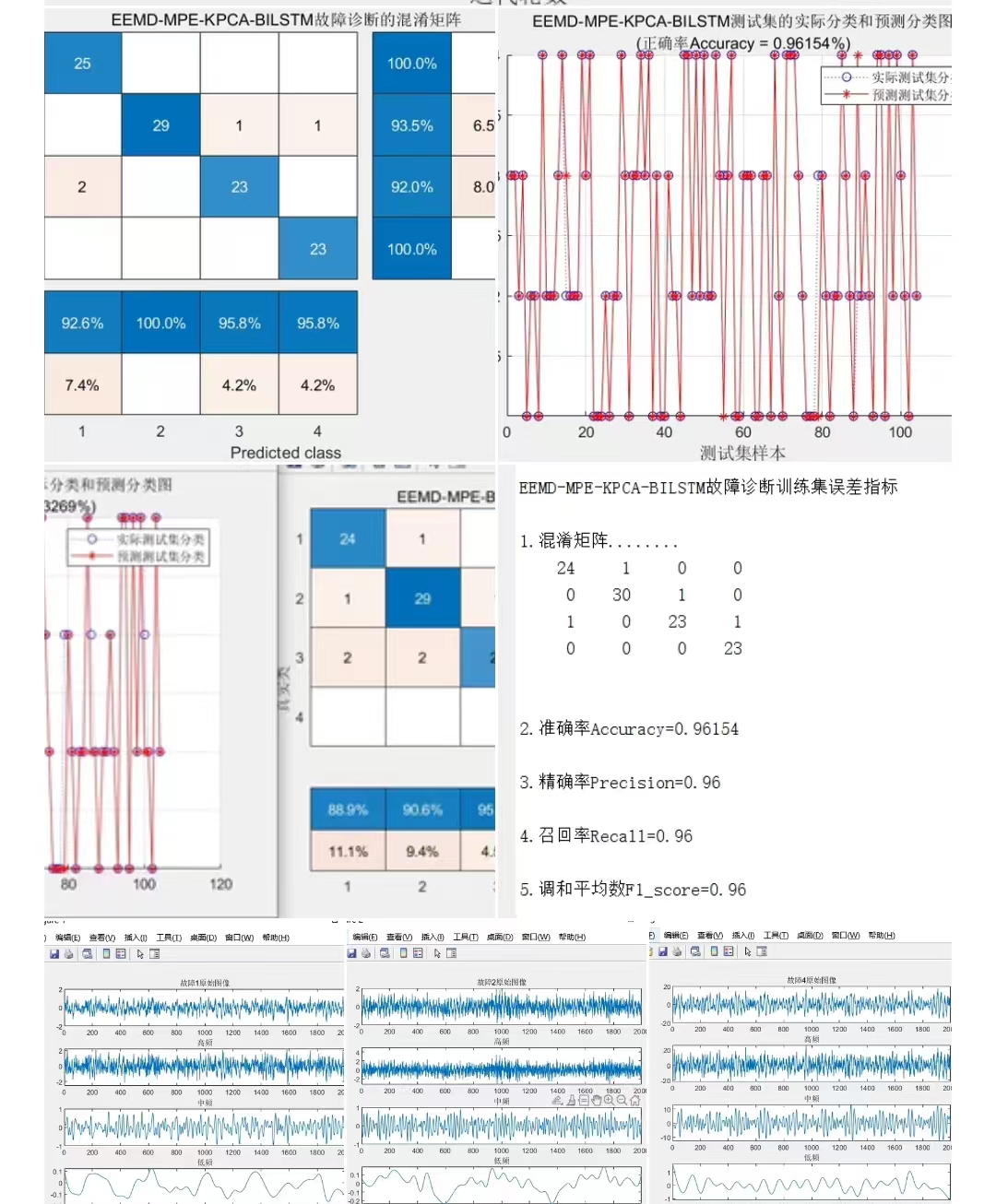
disp('EEMD-MPE-KPCA-BILSTM故障诊断训练集误差指标')
[confmat3,Accuracy3,Precision3,Recall3,F1_score3]=calc_error(T_test3,T_sim2_MSE);
fprintf('\n')
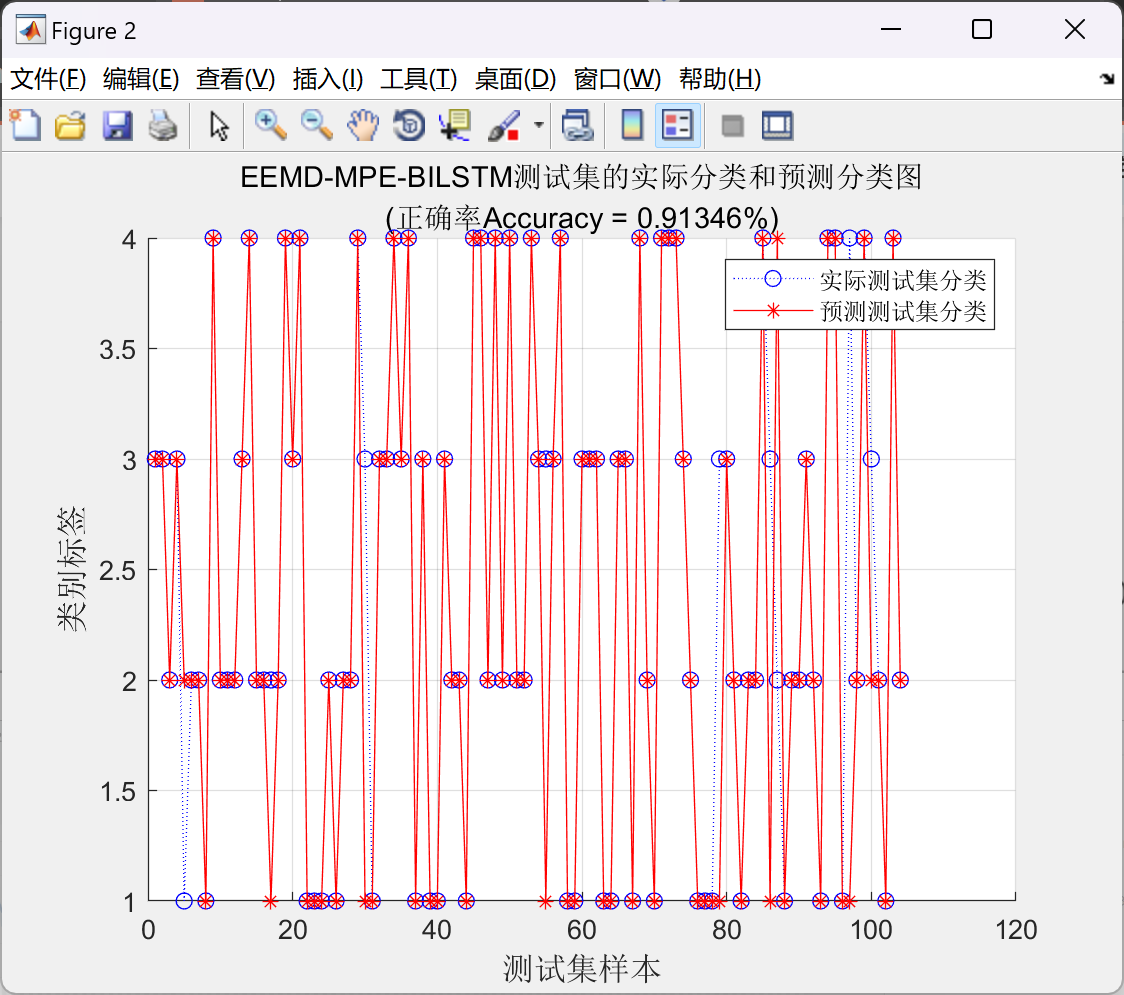
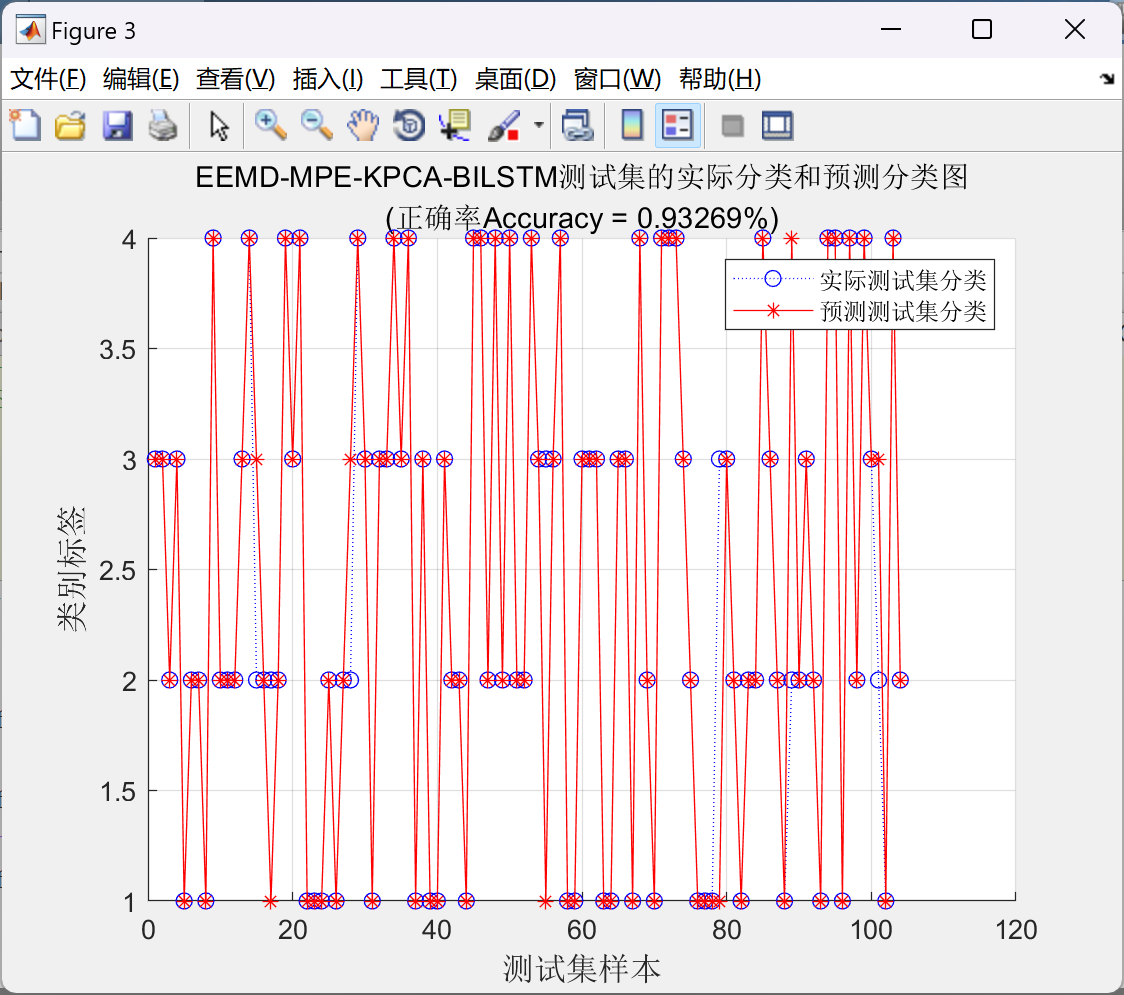
figure;
hold on;
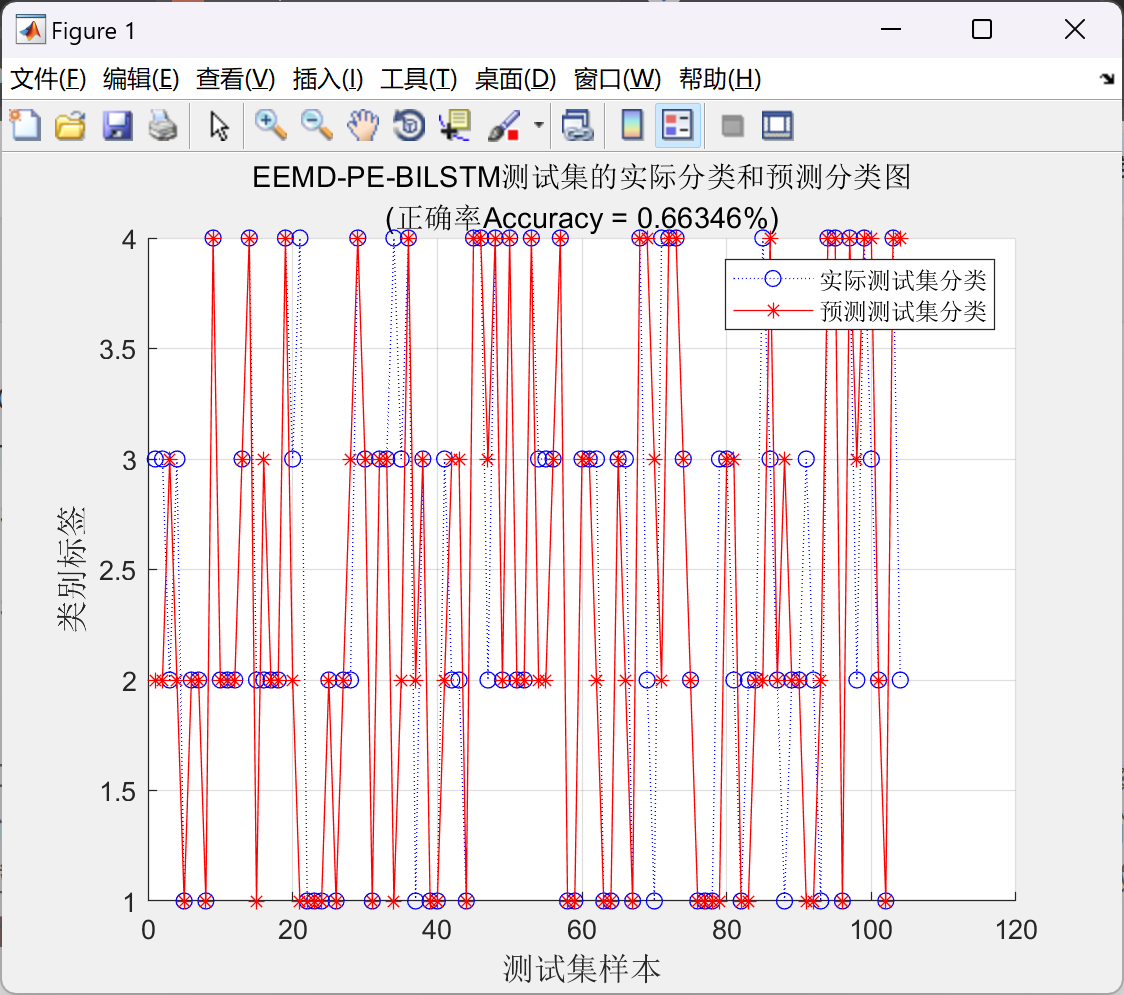
plot(T_test,'b:o');
plot(T_sim2_MSE,'r-*');
xlabel('测试集样本','FontSize',12);
ylabel('类别标签','FontSize',12);
legend('实际测试集分类','预测测试集分类');
string = {'EEMD-MPE-KPCA-BILSTM测试集的实际分类和预测分类图';['(正确率Accuracy = ' num2str(Accuracy3) '%)' ]};
title(string)
grid on;
% 混淆矩阵
figure
cm = confusionchart(T_test3, T_sim2_MSE);
cm.Title = 'EEMD-MPE-KPCA-BILSTM故障诊断的混淆矩阵';
cm.ColumnSummary = 'column-normalized';
cm.RowSummary = 'row-normalized';
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
🌈4 Matlab代码、数据
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取