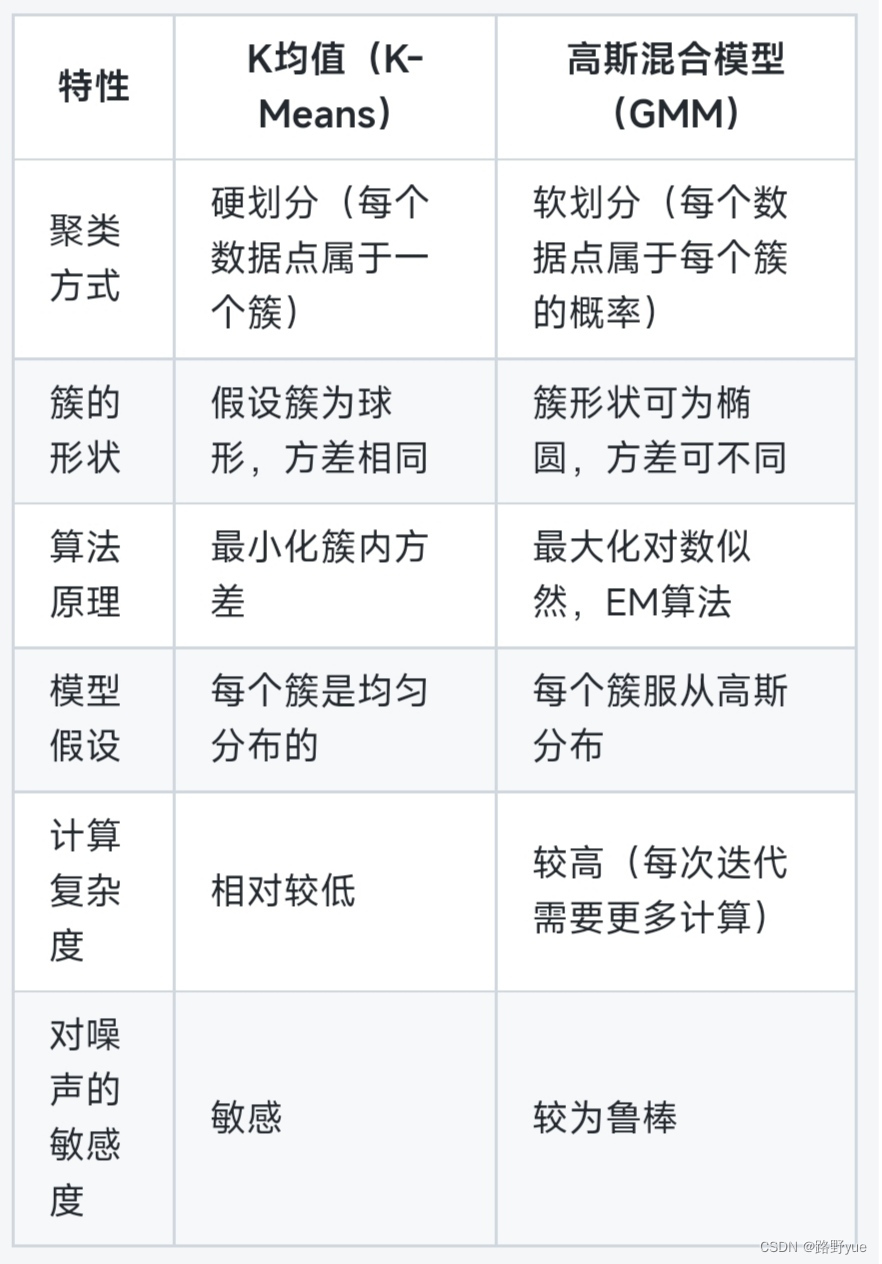
高斯混合模型（Gaussian Mixture Model, GMM）和K均值（K-Means）算法都是常用于聚类分析的无监督学习方法，虽然它们的目标都是将数据分成若干个类别或簇，但在实现方法、假设和适用场景上有所不同。

1. 模型假设

K均值（K-Means）：假设每个簇的样本点在簇中心附近呈均匀分布，通常是球形的（即每个簇的数据点彼此之间的距离相对均匀，具有相同的方差）。每个簇通过一个中心点来表示（即质心），簇内的数据点与质心的距离最小。

高斯混合模型（GMM）：假设数据点来自多个高斯分布的混合体。每个簇不是一个简单的质心，而是由一个高斯分布表示，其中包含了均值、协方差矩阵和混合系数。每个簇的形状不再是球形的，可以是任意的椭圆形，具有不同的方差和协方差。

2. 聚类方式

K均值：基于硬划分（Hard Assignment），即每个数据点被分配到距离其最近的质心的簇中。一个数据点只能属于一个簇。

高斯混合模型（GMM）：基于软划分（Soft Assignment），每个数据点属于每个簇的概率是不同的。通过计算数据点在每个簇中的概率，数据点可能部分属于多个簇，属于每个簇的“隶属度”是概率值。

3. 模型表示

K均值：通过质心来表示每个簇，簇内所有点的分布是均匀的，假设所有簇的形状相同。

高斯混合模型（GMM）：每个簇使用一个高斯分布来表示，包括均值、协方差矩阵（描述簇的形状）和混合系数（表示每个簇在整个数据集中的相对比例）。

 4. 算法优化目标

K均值：通过最小化每个簇内样本点与簇中心的欧几里得距离平方和（即最小化簇内的方差）来优化。

高斯混合模型（GMM）：通过最大化数据的对数似然（log-likelihood）来优化，采用期望最大化（EM）算法进行参数估计。

 5. 适用场景

K均值：适合于簇的形状较为规则（通常是球形簇），簇之间的方差相差不大，且数据量较大的情况。对于噪声和离群点敏感。

高斯混合模型（GMM）：适用于簇形状复杂且可能有不同方差的情况。它能处理簇间形状不同、不同尺度的情形，能够建模非球形的簇。

 6. 算法复杂度

K均值：相对简单，时间复杂度为 O(nkt），其中n是样本数量，k是簇的数量，t是迭代次数。K均值在每次迭代时进行质心计算和数据点分配，通常收敛较快。

高斯混合模型（GMM）：相对复杂，通常采用期望最大化（EM）算法进行参数估计，每次迭代需要计算每个点属于各个簇的概率，并更新高斯分布的参数（均值、协方差和权重）。时间复杂度较高，但每次迭代需要更多的计算。

7. 初始化方式

K均值：质心的初始化对结果有较大影响，通常使用随机选择的方式来初始化质心，或者使用K均值++算法来提高初始化的质量。

高斯混合模型（GMM）：初始化参数（均值、协方差和权重）也是非常关键的，常用的初始化方法是使用K均值算法先初始化簇的均值，然后用它们来估计高斯分布的参数。

8. 对噪声和离群点的敏感度

K均值：对噪声和离群点较为敏感，因为离群点可能会拉偏质心的位置。

高斯混合模型（GMM）：相对来说对噪声和离群点的容忍度较高，因为它通过概率的方式进行分配，不会强制每个点都属于某个簇，而是允许存在“模糊”归属。

总结：

总结：

K均值适用于簇的形状规则且簇内方差相似的情况，算法简单且计算速度较快。

高斯混合模型（GMM）适合簇形状不规则且方差不同的情况，更灵活，但计算复杂度较高。