前言
本篇博客把排序剩下没总结到的知识汇总一下,这样数据结构初阶也算是完了,之前的冒泡,选择,堆,插入,希尔,快排,都说过了,让我们看看还有什么没说到的那
💓 个人主页:小张同学zkf
⏩ 文章专栏:数据结构
若有问题 评论区见📝
🎉欢迎大家点赞👍收藏⭐文章

目录
1.归并排序(递归方法)
基本思想:归并排序( MERGE-SORT )是建立在归并操作上的一种有效的排序算法 , 该算法是采用分治法( Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
我们来看一下动图
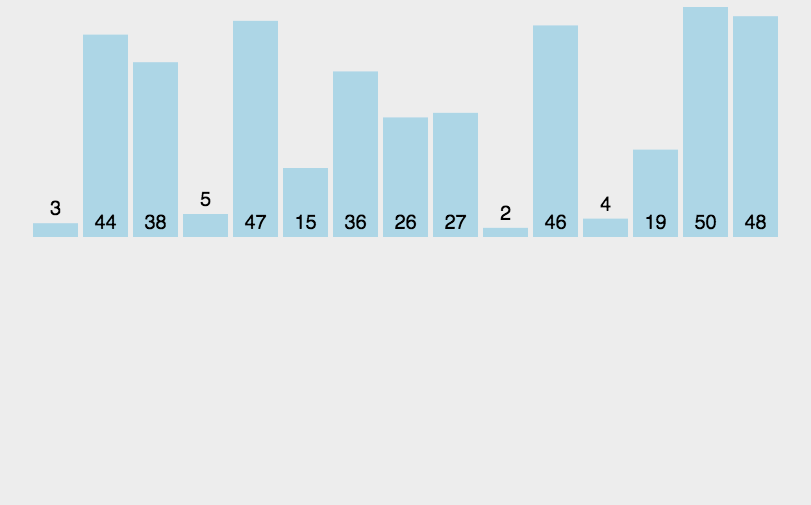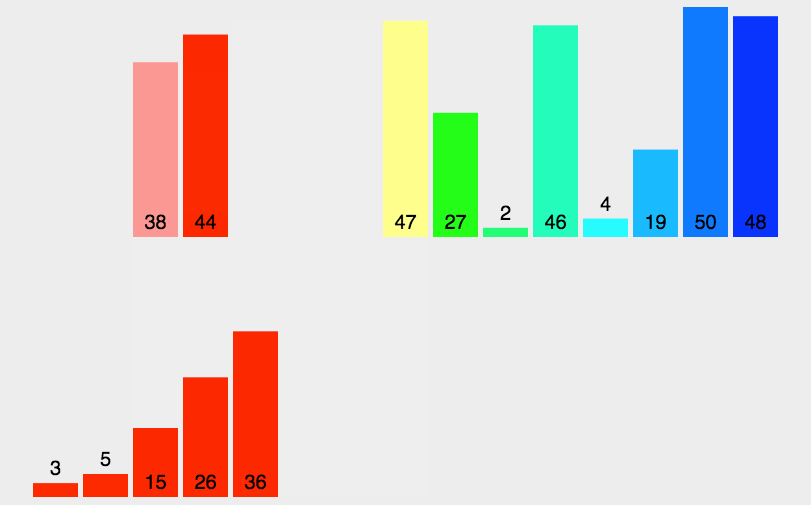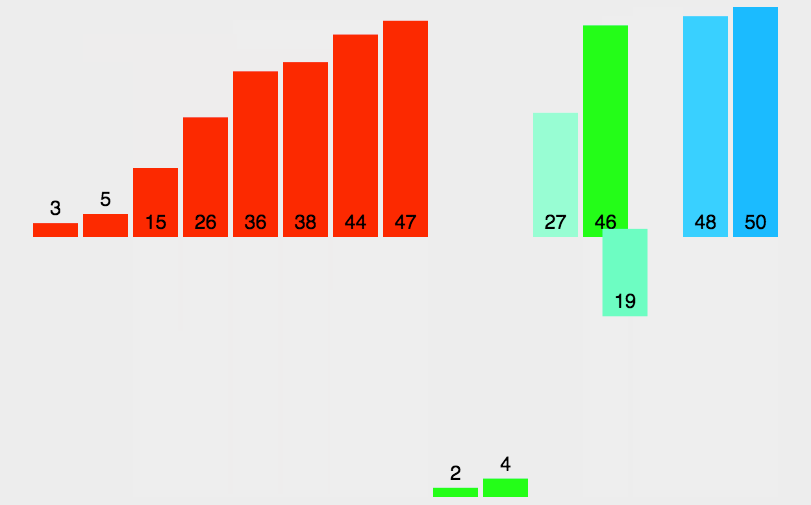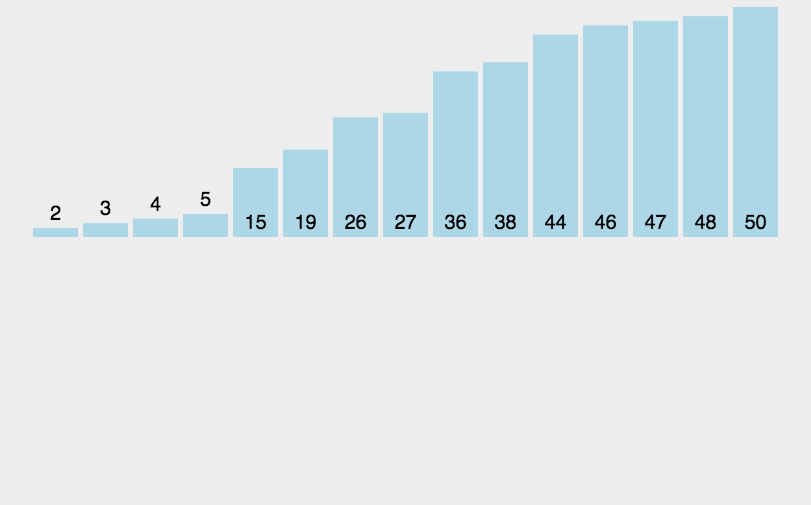
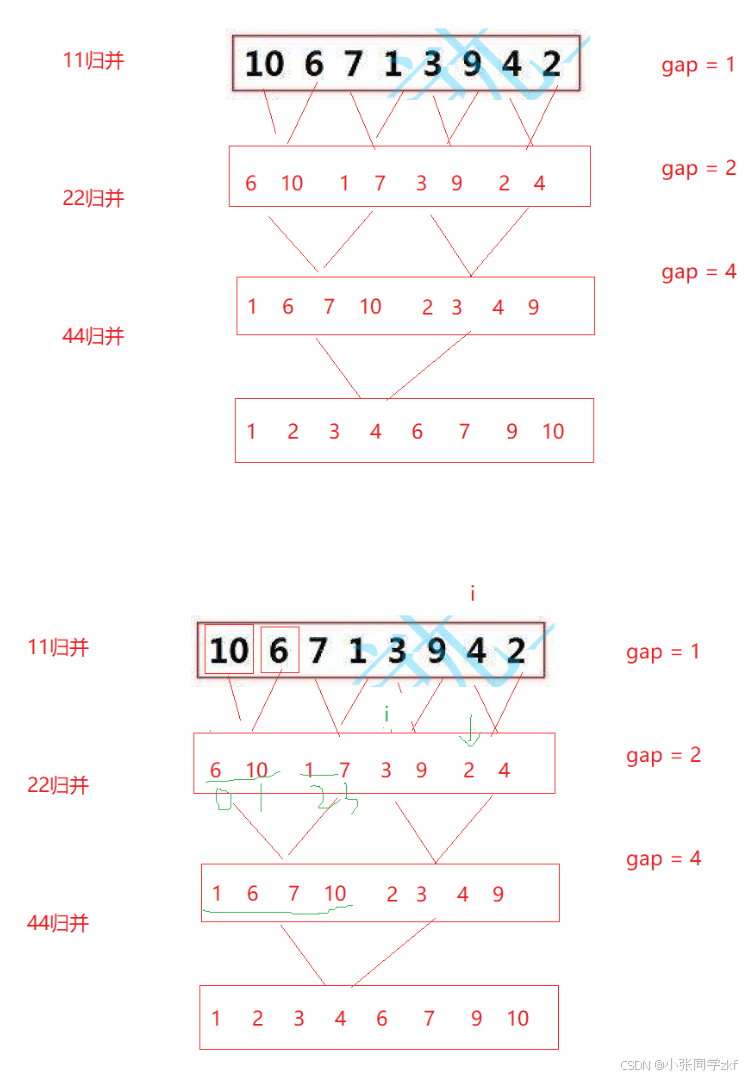
我们画图分析一下
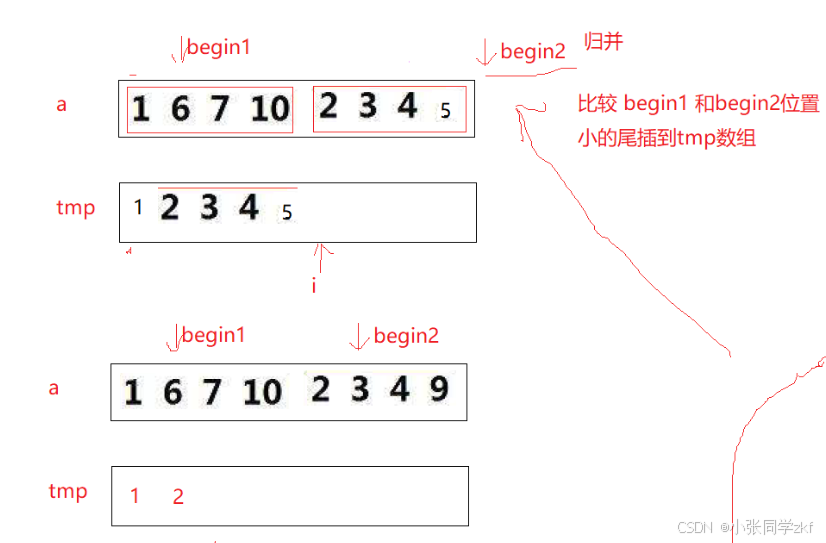
找到中间数据分割,然后比较,在原数组中修改,最后拷贝到新数组中
代码如下
void _mas(int* a, int* tmp, int left, int right)
{
if (left >= right)
return;
int mid = (left + right) / 2;
_mas(a, tmp, left, mid);
_mas(a, tmp, mid + 1, right);
int i = left;
int begin1 = left;
int end1 = mid;
int begin2 = mid + 1;
int end2 = right;
while (begin1<=end1&&begin2<=end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
memcpy(a + left, tmp + left, (right-left+1) * sizeof(int));
}
void guibingpaixu(int* a,int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc");
}
int left = 0;
int right = n - 1;
_mas(a, tmp, left, right);
free(tmp);
}2.归并排序(非递归方法)
快排我们用的非递归方法是通过栈,那么归并的非递归方法按组归并
gap从第一组开始,依次乘2,组数1归并完组数2归并,直到组数等于数据个数,每次归并需要两组,所以归并两组,起始位置要跨两组数据。

但是我们要考虑越界问题,end1,begin2,end2越界问题,假如我们要考虑end1越界,那么此刻begin2与end2必越界,且end2是以二倍增长的,所以它越界时,要把end2赋予最后一个位置的值,以为它极有可能直接跨过最后一组没有归并,至于begin2与end1越界,我们仔细想一下,这俩跨界,我们还需要拍吗,因为这俩跨界根本凑不出来两组,怎么归并,并且这一组也是提前归并好的是有续的,所以不需要归并。
代码如下
void guibing(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i = i + 2 * gap)
{
int begin1 = i;
int end1 = i + gap-1;
int begin2 = i + gap;
int end2 = i + 2 * gap - 1;
if (begin2 >= n)
{
break;
}
if (end2 >= n)
{
end2 = n - 1;
}
int j = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));
}
gap = gap * 2;
}
free(tmp);
tmp = NULL;
}
3.归并排序特性
归并排序的特性总结:1. 归并的缺点在于需要 O(N) 的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。2. 时间复杂度: O(N*logN)(原理在于递归方式与二叉树相似)3. 空间复杂度: O(N)(开辟了一个新的动态数组空间)4. 稳定性:稳定
4.计数排序(非比较排序)
这个排序不常用不过还是点一下
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。 操作步骤:
1.
统计相同元素出现次数
2.
根据统计的结果将序列回收到原来的序列中
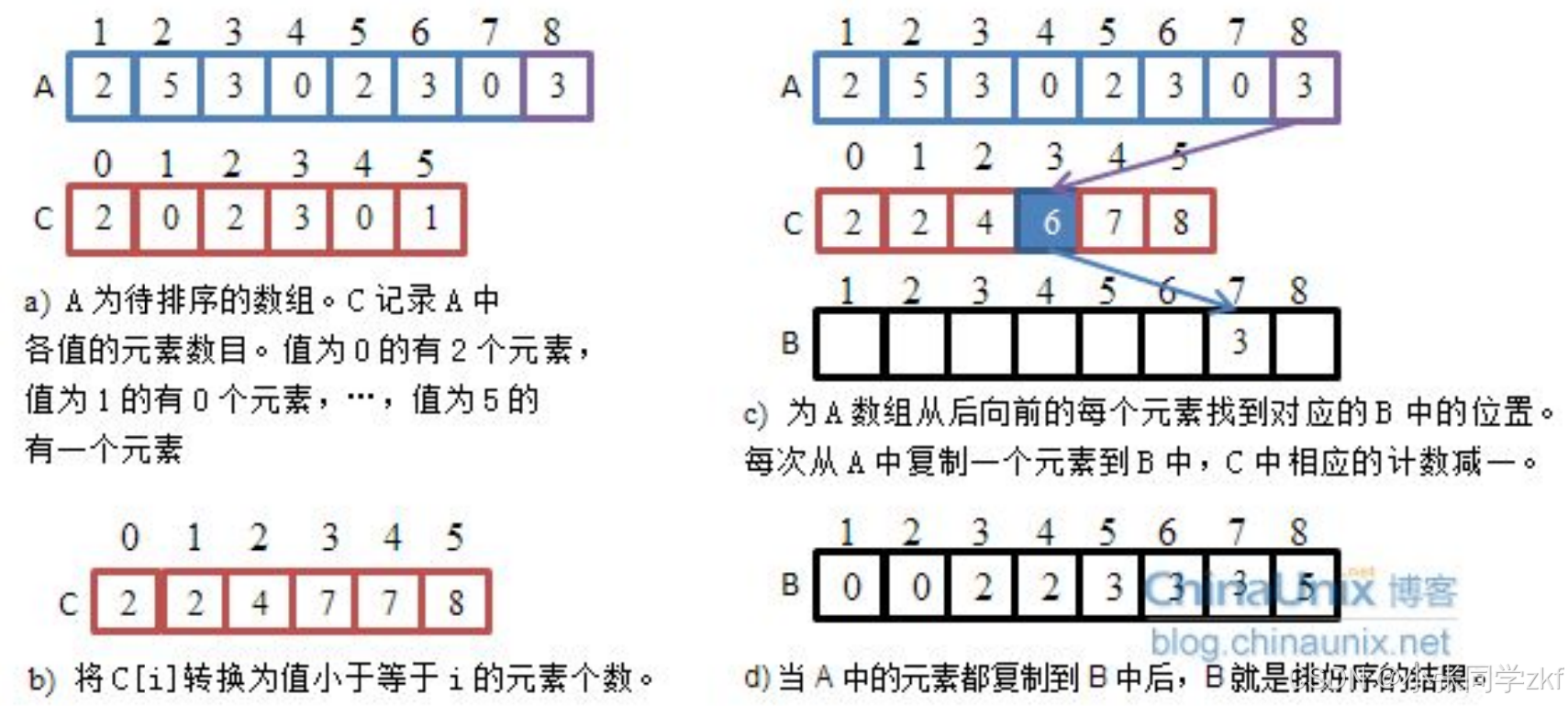
过程如下图


代码如下
void jishu(int* a, int n)
{
int min = a[0];
int max = a[0];
for (int i = 1; i < n; i++)
{
if (a[i] < min)
{
min = a[i];
}
if (a[i] > max)
{
max = a[i];
}
}
int range = max - min + 1;
int* tmp = (int*)calloc(range, sizeof(int));
if (tmp == NULL)
{
perror("calloc");
return;
}
for (int i = 0; i < n; i++)
{
tmp[a[i]-min]++;
}
int as = 0;
for (int j = 0; j < range; j++)
{
while (tmp[j]--)
{
a[as++] = j + min;
}
}
}
计数排序的特性总结:1. 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。2. 时间复杂度: O(MAX(N, 范围 ))3. 空间复杂度: O( 范围 )4. 稳定性:稳定
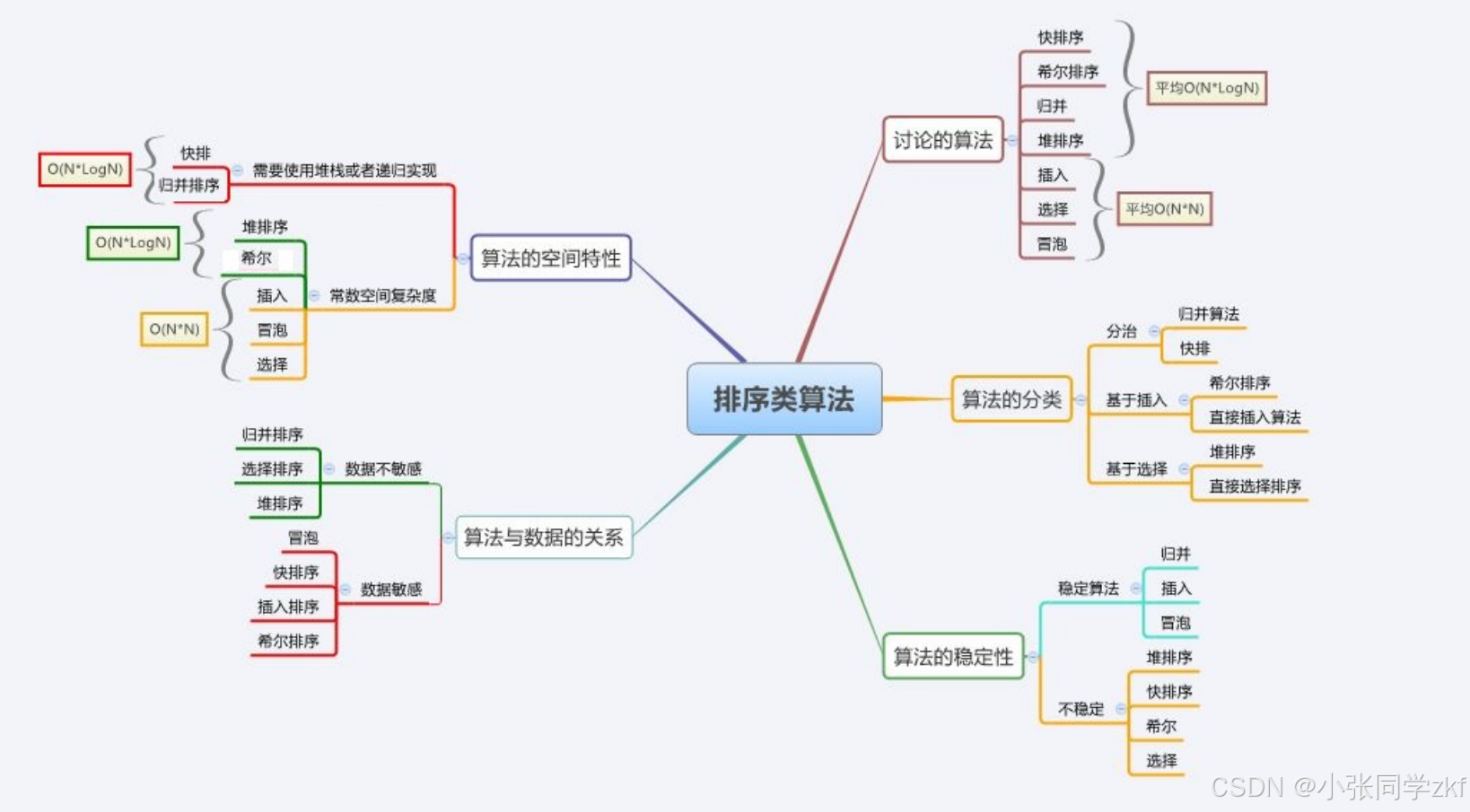
5.排序算法复杂度及稳定性分析
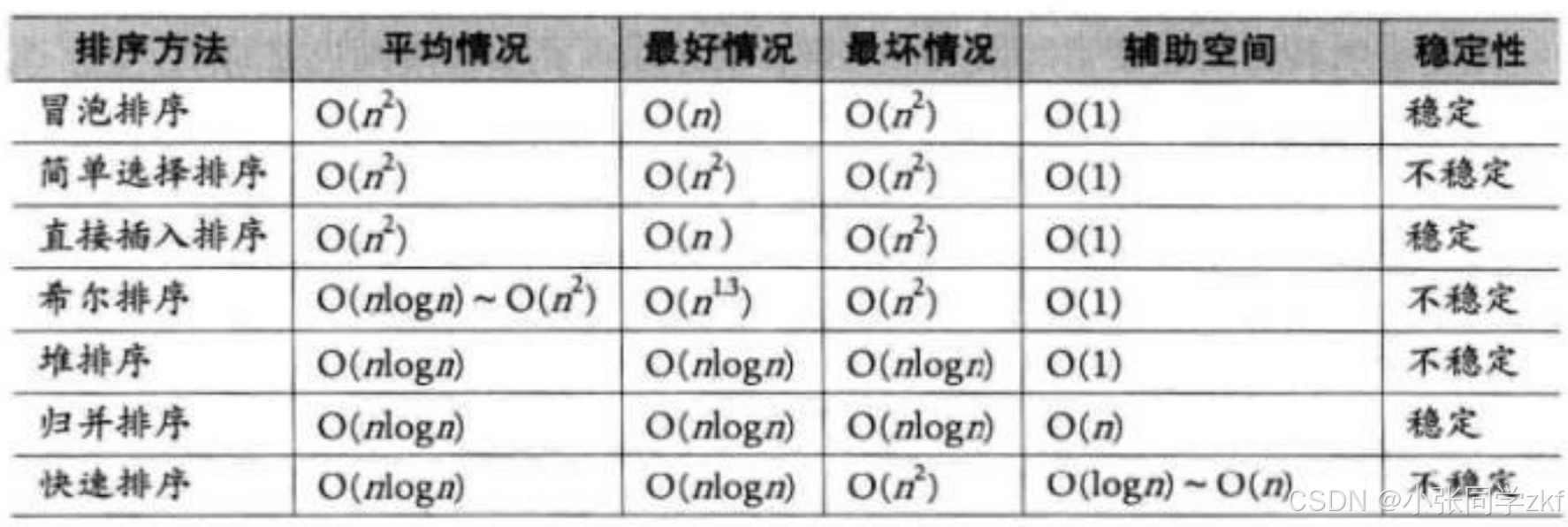
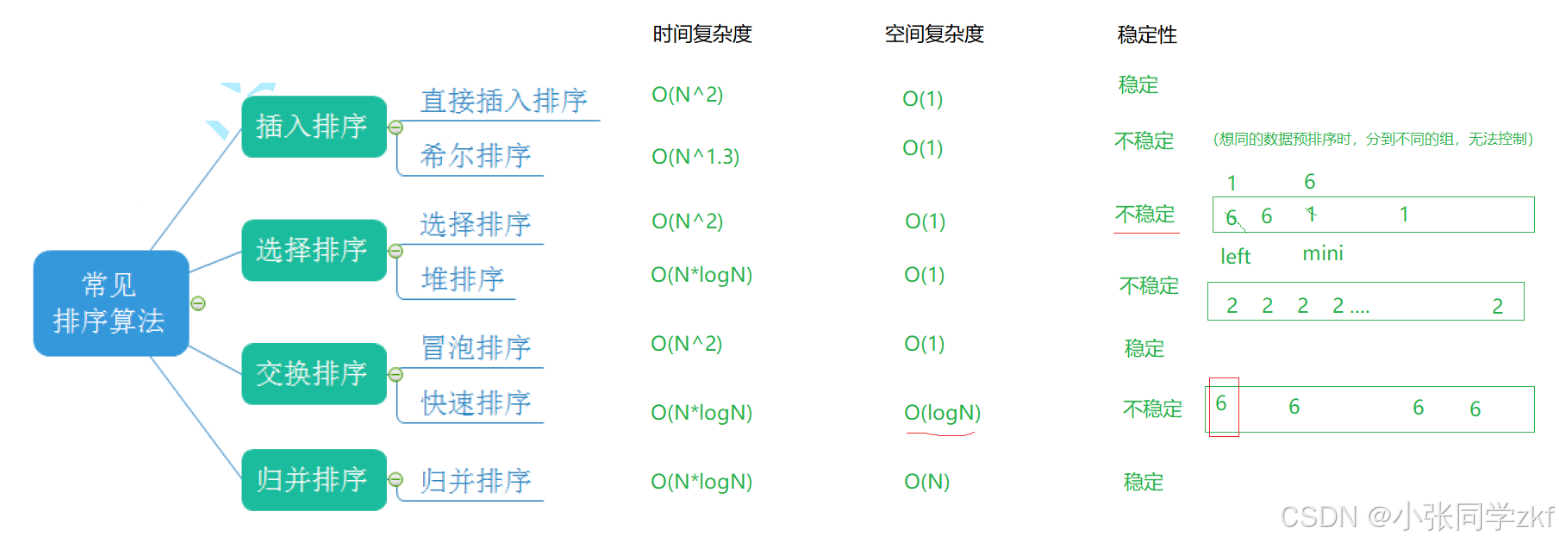
结束语
OK排序这一系列就暂时总结完了,初阶数据结构这一块也就结束了,下一部分就开始正式C++知识总结,进入C++这一部分,难度会直线上升,大家一起努力
OK,本篇博客结束!!!