一: KMP介绍
KMP:通常用来处理字符串匹配类型问题
例如:当你遇到一个问题,需要在父字符串当中去寻找一串给定的子字符串的位置或者数量的问题时,就可以用到KMP算法去解决这个问题。例如下面这个问题。
二: KMP分析
1. 思路分析
1.1传统思路
对于一般的思路我们可以对于父字符串的每个位置作为一个起始,再使用子字符串去逐个匹配若匹配完全成功则记录下这个结果的方法。
弊端:显然这个过程是最暴力的一个过程,其时间复杂度是O(N*M)的,这很明显并不是一个最优的方法,所以我们需要对于其匹配的过程再进行一个分析尝试找到一些地方可以优化我们的过程。
1.2 优化思路
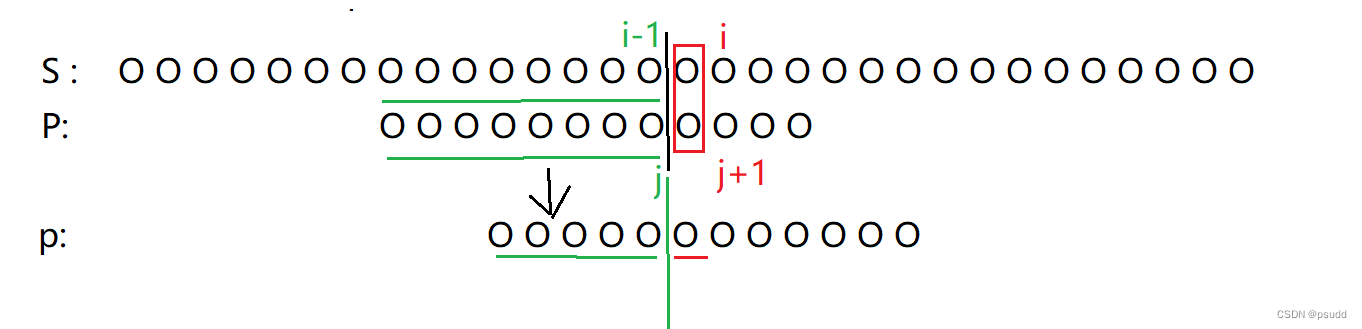
选取匹配过程一般状态分析: char s[ ]为父字符串,需要被去匹配的字符串.令 char p[ ]为子字符串,要拿去进行匹配的字符串
第1步. 我们假设已经匹配了一段长度(即绿色部分),而匹配到红色的那个字符时出现错误并不符合,即如下:
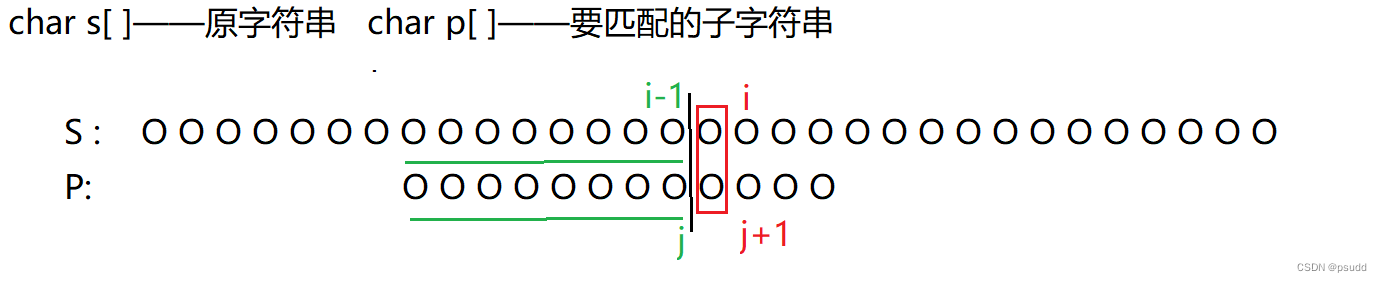
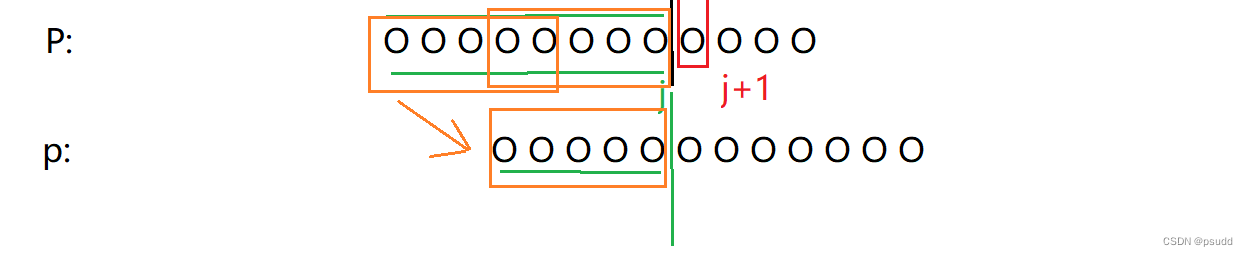
第3步. 那现在我们可以发现一个有趣的地方,当这个过程可以被实现后P会出现一些有趣的性质.
对比两次P的地方,发现P字符串会有一些重复的地方,即如下图的3个橙色的部分 ,因为P是横移过来的,显然前面一部分是一样的,而又因为P横移过后前面又可以和上面的S进行匹配,所以P后面一部分和P前面一部分应该是一样的内容
第4步. 这其实就是我们需要寻找的一个快捷的地方了,这样我们就可以每次会移动多个距离。
即 我们要记录下P字符串上每个位置的后缀和从P开头的前缀最长的一样部分的长度(因为要保证每次移动距离尽可能短,所以储存的一定是最长重复的长度),将这个值用ne[ ] 数组来存储,例如上图我们可以认为是将P向后移动了ne[j] = 3的一个长度
ne[ ]数组的解析如下图所示:
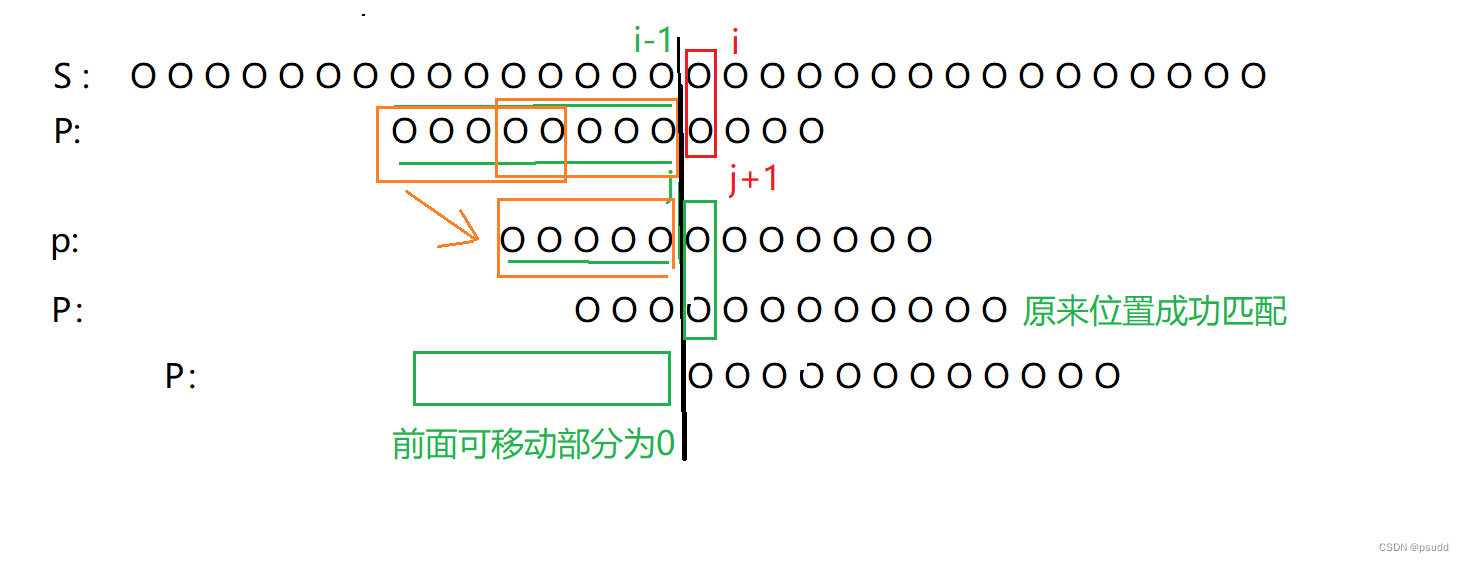
第5步 :这样我们就可以从开始去匹配这个字符串了,当遇到第一个不匹配的地方的时候,我们就调用j=ne[j]去移动这个子字符串,再去匹配原来位置的字符串,直到可以匹配或者前面可移动的重复部分的长度为0的时候(即ne[j]=0)的时候我们停止匹配。
如图:不断后移,直到原来位置匹配成功,或者前面可移动的部分为空
2. 细节注意
2.1:i 要和 j+1 进行比较
父字符串从i开始匹配到第i个字符串可以理解,但是为什么要与子字符串的 j+1进行匹配呢?
因为可以方便代码的书写,因为j还可以同时表示已经匹配的长度。 当不匹配到不相同的时候 j = ne[j],然后继续用 i 和 j+1 进行比较。
2.2:保证 ne[x] < x
因为ne[j]是移动的一个距离,如果确实存在 a a a a这个字符串,我们也不可能说 ne[1]=1,ne[2]=2,ne[3]=3,ne[4]=4,因为这个样子 j=ne[j]会进入死循环,所以这个前缀和后缀重复部分长度永远都不能完全重复自身,我们规定ne[1]=0。
三: KMP代码
1. 代码解析
p[]需要进行匹配的子串,s[]是父字符串
p[]的长度为n,s[]的长度为m
char p[N],s[M];
1.1 KMP匹配过程代码
s[]父字符串,p[]为子字符串
初始状态已经匹配的长度j=0,i从初始位置开始 i=1
for(int i=1,j=0;i<=m;i++){
1.当j>0依旧可以移动并且s[i]和p[j+1]依旧不匹配,不断移动
while(j&&s[i]!=p[j+1]) j=ne[j];
1.跳出循环后,如果是已经匹配,那么j++,匹配下一个位置
2.如果是因为j=0导致的不匹配,那么j=0,相当于继续下一个i并且和j
子字符串从头开始匹配
if(s[i]==p[j+1]) j++;
1.如果匹配长度j==n,就证明有这个子字符串,输出起始位置的坐标
(坐标从0开始)
if(j==n){
cout<<i-n<<" ";
}
}
1.2 ne[ ]数组求解过程代码
核心:同时将自己作为父字符串和子字符串进行匹配的过程
求解过程起始可kmp匹配相似,就是将自己同时当作父字符串和子字符串进行匹配。
但我们并不需要j==n才输出结果,我们可以将每次匹配到i位置的时候,
j就是代表已经匹配部分的长度,直接赋值给ne[i]=j即可
1.我们规定了ne[x]<x,所以ne[1]=0,位置直接从i=2开始
for(int i=2,j=0;i<=n;i++){
while(j&&p[i]!=p[j+1]) j=ne[j];
if(p[i]==p[j+1]) j++;
1.每次将当前位置的已经匹配的长度进行记录即可
ne[i]=j;
}
2. 完整代码
2.1 完整代码
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10,M=1e6+10;
char p[N],s[M]; // p是需要进行匹配的子串
int ne[N];
int main(){
int n,m;
cin>>n>>p+1>>m>>s+1;
for(int i=2,j=0;i<=n;i++){
while(j&&p[i]!=p[j+1]) j=ne[j];
if(p[i]==p[j+1]) j++;
ne[i]=j;
}
for(int i=1,j=0;i<=m;i++){
while(j&&s[i]!=p[j+1]) j=ne[j];
if(s[i]==p[j+1]) j++;
if(j==n){
cout<<i-n<<" ";
}
}
}
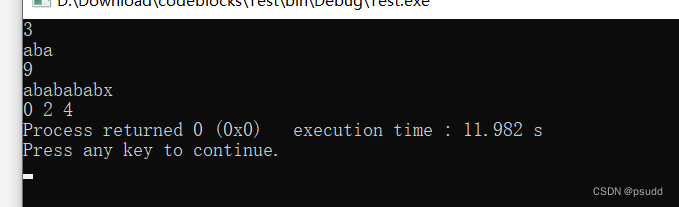
2.2 运行结果
输入子字符串: aba , n=3 父字符串: ababababx , m=9
预计结果位置为:0 , 2 , 4