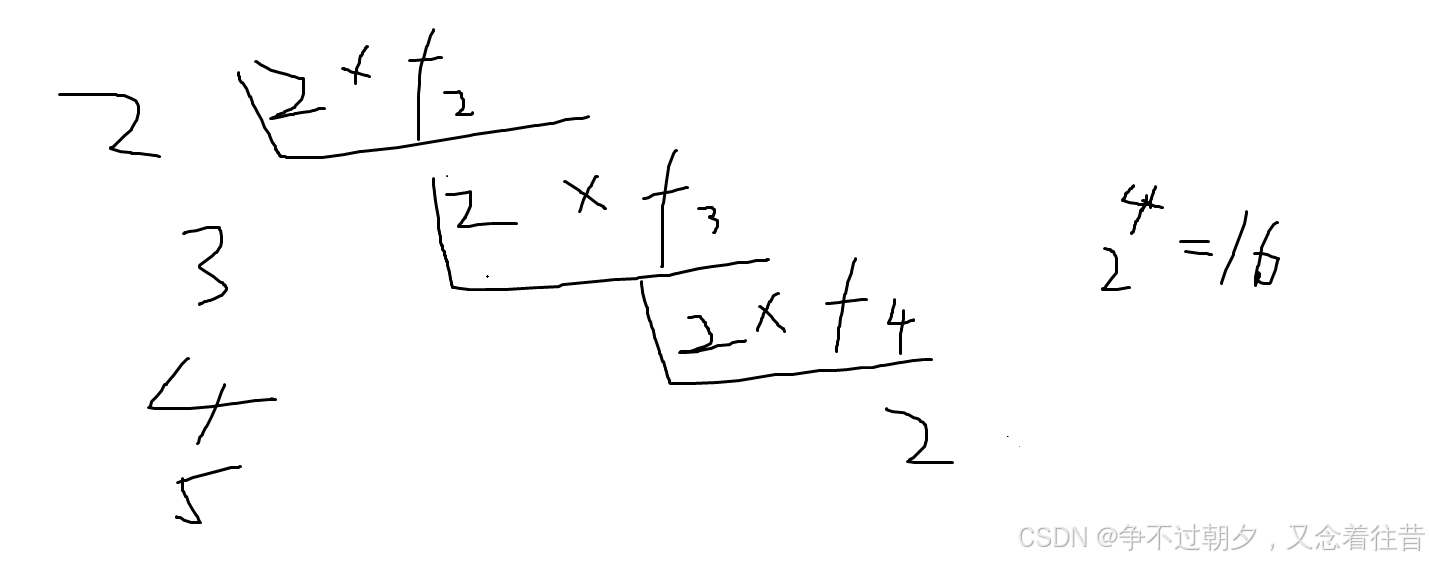一、选择题

1-5题

%o就是输出八进制的无符号数，0123，，以0开头·，本来就是八进制，所以输出为123，123是十进制，转化为八进制就是173.
故选C。

1. %d 或 %i：用于输出 int 类型的整数。
2. %u：用于输出无符号 int 类型的整数。
3. %ld 或 %li：用于输出 long int 类型的整数。
4. %lld 或 %lli：用于输出 long long int 类型的整数。
5. %o：用于输出无符号整数，以八进制形式显示。
6. %x 或 %X：用于输出无符号整数，以十六进制形式显示（%x 生成小写字母，%X 生成大写字母）。
7. %f：用于输出 float 或 double 类型的浮点数。
8. %c：用于输出单个字符。
9. %s：用于输出字符串。
10. %p：用于输出指针变量的值。
11. %e：用于输出浮点数，采用科学计数法。
12. %g：根据数值和精度，自动选择 %f 或 %e 格式。
13. %%：用于输出 % 字符。

A选项，2二进制是10，~2是01，flag和它进行与运算，同1才是1，所以，第二位一定会被置0.
故选A。

1. 位与（AND）：&

   • 用法：result = a & b;
   • 功能：对a和b中的每一位执行逻辑与操作。如果两位都是1，则结果的该位是1，否则是0。

2. 位或（OR）：|

   • 用法：result = a | b;
   • 功能：对a和b中的每一位执行逻辑或操作。如果两位中至少有一位是1，则结果的该位是1，否则是0。

3. 位非（NOT）：~

   • 用法：result = ~a;
   • 功能：对a中的每一位执行逻辑非操作。如果某位是1，则结果的该位是0，如果某位是0，则结果的该位是1。

4. 位异或（XOR）：^

   • 用法：result = a ^ b;
   • 功能：对a和b中的每一位执行逻辑异或操作。如果两位不同，则结果的该位是1，如果两位相同，则结果的该位是0。

5. 左移：<<

   • 用法：result = a << n;
   • 功能：将a的二进制表示向左移动n位。右边空出的位用0填充。

6. 右移：>>

   • 用法：result = a >> n;
   • 功能：将a的二进制表示向右移动n位。对于无符号数，左边空出的位用0填充；对于有符号数，具体行为（用0填充还是用符号位填充）取决于编译器。

使用位运算时，需要注意操作的数通常是整数类型，而且位运算直接对内存中的位进行操作，因此效率很高。同时，位运算也可以用于实现一些特定的算法，比如快速计算2的幂、交换两个数的值而不使用临时变量等。

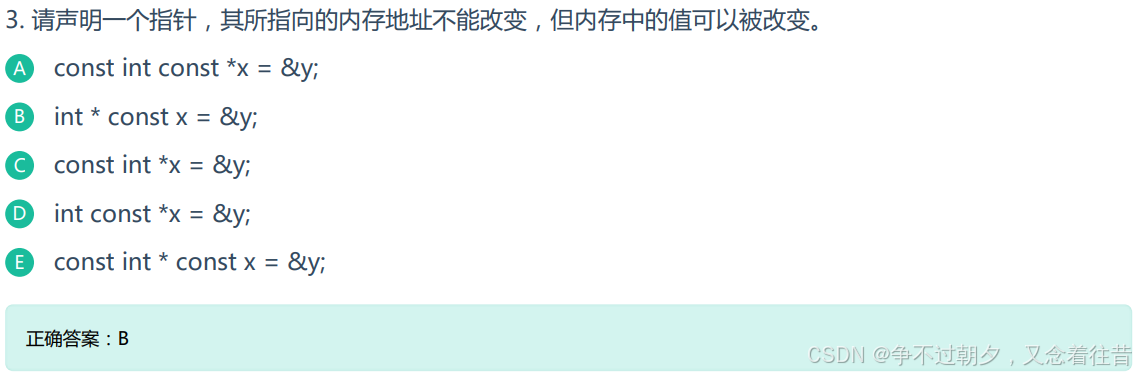
指向内存地址不能改变，指针常量，const在*右边，故选B。
A：const都在*前都是指向可以修改，但指向空间的内容不能改。

B：x指针指向不能修改，但是指向空间中的内容是可以修改

C：x指向可以修改，但是指肉空间中的内容不能修改

D：x指向可以修改，但是指向空间中的内容不能修改

E：x指针的指向不能修改，指针指向空间中的内容也不能修改

const在*前:const修饰的是解引用的结果不能修改，即指向执行空间中的内容不能修改
const在*后:const修饰指针变量本身，即指针的值不能修改，指针的指向不能修改

a是数组名，&a表示数组的地址，&a+1表示指针偏移一个数组的大小，即5个int大小的字节数，因此&a+1指向数组最后一个元素的下一个元素，在强转为int*，进行±操作移动的步长就会改变成一个int大小，因此，p-1指向元素9，*（p-1）就是9。而a是数组首元素，a+1，指向数组第二个元素，解引用完就是3.
故选C。

知识点，数组名是数组首元素的地址，&数组名是数组的地址，相同点，都指向同一个位置，不同点±操作移动的步长不一样。

不知道总共有多少行，每行有多少列
假设:数组X的起始地址为start，总共有M行，N列

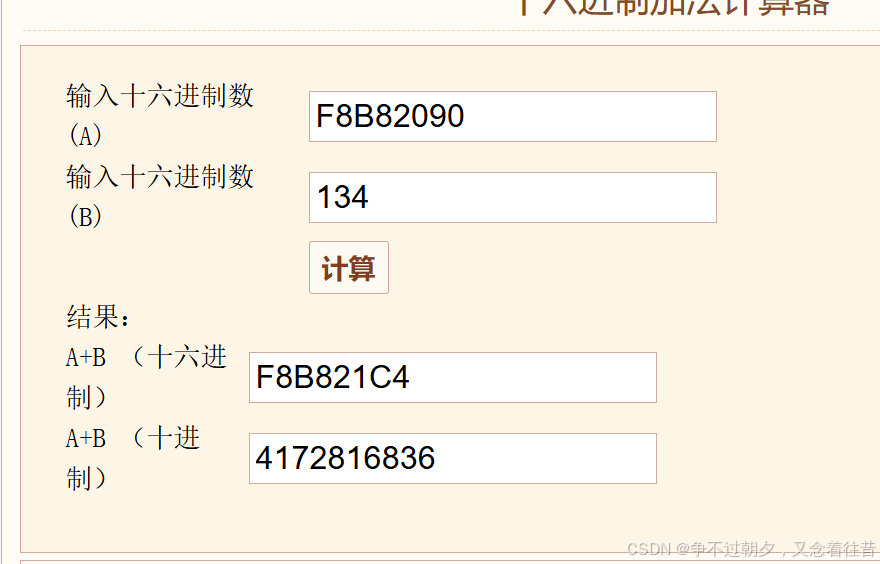
&x[4][4]= start+ 4N+4=0xf8b82140
&x[9][9]= start + 9N+9 = 0xf8b8221c
上面这是个方程组嘛，两个方程组两个未知数，解一下，得到
start=0xF8B82090
N=43

&x[7][7]= start + 7*N+7=F8B821C4

故选A。

6-10题

如图2^4＝16
故选D。

数组名表示数组首元素的地址，只有在&和sizeof之后才表示数组的本身
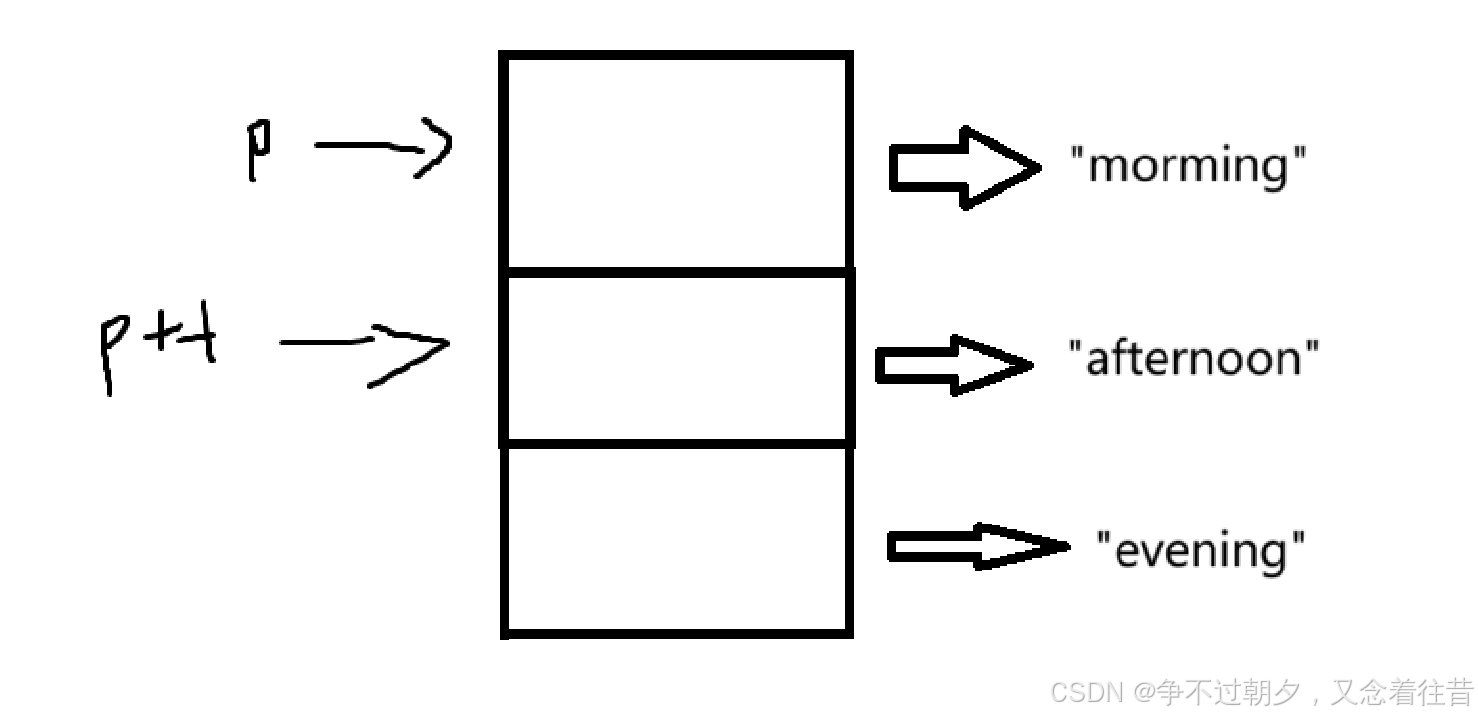
"morning"的类型是char*
p=a;p就必须给成二级指针

p原先指向第一个字符串，++之后就是指向第二个字符串，故选A。

假设x=7---->111
x=7&6=111&110=110 x=6
第-次循环:count+±–>count:1
第二次循环:count+±–>count:2 x=6&5=110&101=100 x=4
第三次循环:count+±–>count:3 x=4&3=100&011=0
最终返回的就是3

由此可以看出该函数的功能:返回x中总共有多少个1
因此把9999换算成二进制看它有几个1就好，把9999换成二进制就是10011100001111一共有8个1，所以选A。

FO递归1次
F1递归1次
F2:FO+F1=递归3次
F3:F2+F1=1+3+1 =5
F4:F3+F2=1+5+3=9
F5:F4+F3=1+9+5=15
F6:F5+F4=1+15+9=25
F7:F6+F5=1+25+15=41
F8:F7+F6=1 + 41 + 25 =67

故选B。

1.结构体为什么要对齐?
2.结构体是如何进行对齐?
3.如果想要让结构体按照任意字节对齐该如何处理?

结构体对齐:
1.保证每个成员都放在一个对齐的地址上=== min(该成员类型大小 ， 对齐参数) 能否被偏移量整除
如果可以被整除，则在对齐的地址上
如果不可以被整除，则需要补一些字节让其可以整除
第一步算完之后，结构体已经有了一个总的大小
2.对结构体整体来对齐:min(在数组中找类型最大的成员所占字节,对齐参数)看能否被第一步算出来的结构体的大小整除
如果可以被整除，则在对齐的地址上
如果不可以被整除，则需要补一些字节让其可以整除

故选C。

二、编程题

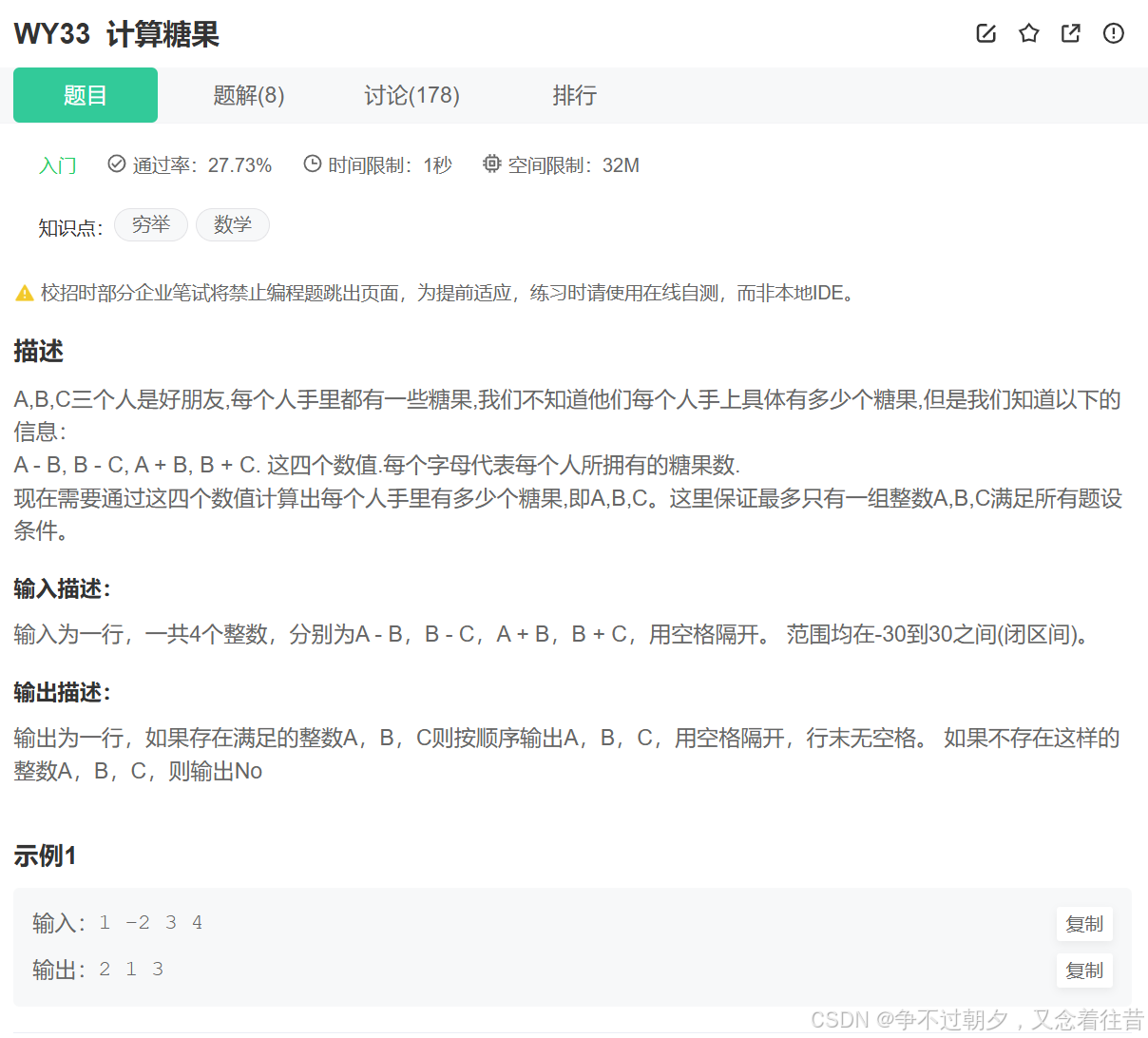
题目一

题目链接：
计算糖果

提交代码：

#include <iostream>
using namespace std;

int main() {
    int a,b,c,d;
    while(cin>>a>>b>>c>>d)
    {
        //A-B=a
        //B-C=b
        //A+B=c
        //B+C=d
        int A=(a+c)/2;
        int B1=(c-a)/2;
        int B2=(b+d)/2;
        int C=(d-b)/2;
        if(B1!=B2)
        {
            cout<<"No";
        }
        else {
        {
            cout<<A<<" "<<B1<<" "<<C;
        }
        }
    }

}
// 64 位输出请用 printf("%lld")

运行结果：

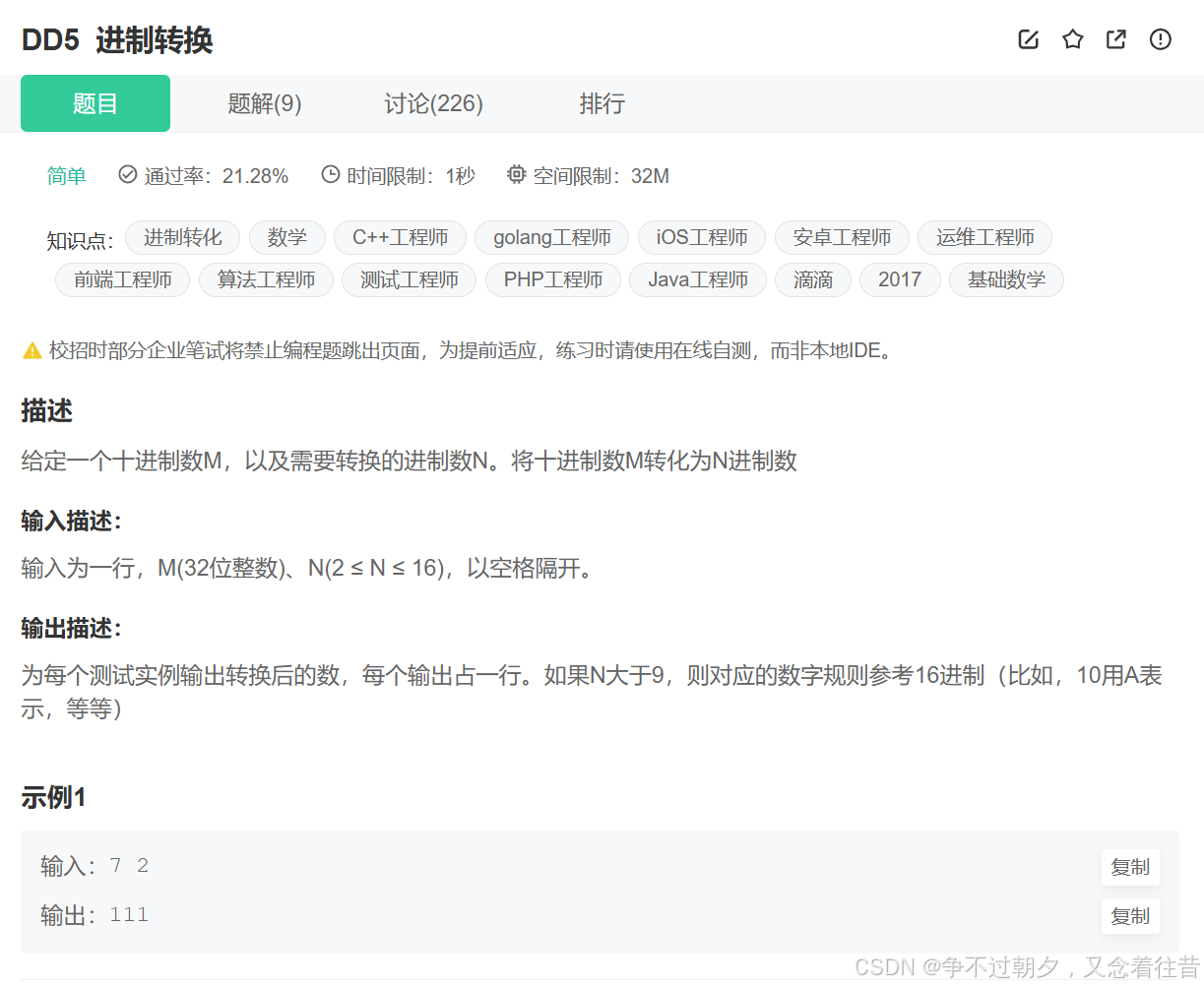
题目二

题目链接：
进制转换

提交代码：

#include <algorithm>
#include <string>
#include <iostream>
using namespace std;

int main() {
    string s,table="0123456789ABCDEF";
    int m,n;
    bool flag=false;
    cin>>m>>n;
    if(m==0)
    {
        cout<<0;
    }
    if(m<0)
    {
        m=0-m;
        flag=true;
    }
    while(m!=0)
    {
        s+=table[m%n];
        m/=n;
    }
    if(flag) s+='-';
    reverse(s.begin(), s.end());
    cout<<s;
    return 0;

}
// 64 位输出请用 printf("%lld")

运行结果：