文章目录
排序算法
概述
比较排序算法
| 算法 | 最好 | 最坏 | 平均 | 空间 | 稳定 | 思想 | 注意事项 |
|---|---|---|---|---|---|---|---|
| 冒泡 | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | Y | 比较 | 最好情况需要额外判断 |
| 选择 | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | N | 比较 | 交换次数一般少于冒泡 |
| 堆 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O(1) | N | 选择 | 堆排序的辅助性较强,理解前先理解堆的数据结构 |
| 插入 | O(n) | O( n 2 n^2 n2) | O( n 2 n^2 n2) | O(1) | Y | 比较 | 插入排序对于近乎有序的数据处理速度比较快,复杂度有所下降,可以提前结束 |
| 希尔 | O(nlogn) | O( n 2 n^2 n2) | O( n l o g n nlogn nlogn) | O(1) | N | 插入 | gap序列的构造有多种方式,不同方式处理的数据复杂度可能不同 |
| 归并 | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O( n l o g n nlogn nlogn) | O(n) | Y | 分治 | 需要额外的O(n)的存储空间 |
| 快速 | O( n l o g n nlogn nlogn) | O( n 2 n^2 n2) | O( n l o g n nlogn nlogn) | O(logn) | N | 分治 | 快排可能存在最坏情况,需要把枢轴值选取得尽量随机化来缓解最坏情况下的时间复杂度 |
非比较排序算法
| 非比较排序算法 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 计数排序 | O(n+k) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n+k) | 稳定 |
| 基数排序 | O(d*(n+k)) | O(n+k) | 稳定 |
其中
- n 是数组长度
- k 是桶长度
- d 是基数位数
稳定 vs 不稳定
Java 中的排序
Arrays.sort
JDK 7~13 中的排序实现
| 排序目标 | 条件 | 采用算法 |
|---|---|---|
| int[] long[] float[] double[] | size < 47 | 混合插入排序 (pair) |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| byte[] | size <= 29 | 插入排序 |
| size > 29 | 计数排序 | |
| char[] short[] | size < 47 | 插入排序 |
| size < 286 | 双基准点快排 | |
| 有序度低 | 双基准点快排 | |
| 有序度高 | 归并排序 | |
| size > 3200 | 计数排序 | |
| Object[] | -Djava.util.Arrays.useLegacyMergeSort=true | 传统归并排序 |
| TimSort |
JDK 14~20 中的排序实现
| 排序目标 | 条件 | 采用算法 |
|---|---|---|
| int[] long[] float[] double[] | size < 44 并位于最左侧 | 插入排序 |
| size < 65 并不是最左侧 | 混合插入排序 (pin) | |
| 有序度低 | 双基准点快排 | |
| 递归次数超过 384 | 堆排序 | |
| 对于整个数组或非最左侧 size > 4096,有序度高 | 归并排序 | |
| byte[] | size <= 64 | 插入排序 |
| size > 64 | 计数排序 | |
| char[] short[] | size < 44 | 插入排序 |
| 再大 | 双基准点快排 | |
| 递归次数超过 384 | 计数排序 | |
| size > 1750 | 计数排序 | |
| Object[] | -Djava.util.Arrays.useLegacyMergeSort=true | 传统归并排序 |
| TimSort |
- 其中 TimSort 是用归并+二分插入排序的混合排序算法
- 值得注意的是从 JDK 8 开始支持 Arrays.parallelSort 并行排序
- 根据最新的提交记录来看 JDK 21 可能会引入基数排序等优化
外部排序
1) 冒泡排序
要点
- 每轮冒泡不断地比较相邻的两个元素,如果它们是逆序的,则交换它们的位置
- 下一轮冒泡,可以调整未排序的右边界,减少不必要比较
以数组 3、2、1 的冒泡排序为例,第一轮冒泡
第二轮冒泡
未排序区域内就剩一个元素,结束
优化手段:每次循环时,若能确定更合适的右边界,则可以减少冒泡轮数
以数组 3、2、1、4、5 为例,第一轮结束后记录的 x,即为右边界
x之后的元素,在此轮排序中没有交换位置,他们是有序的,不需要进行下一轮排序
非递归版代码
采用优化手段后的冒泡排序才有可能时间复杂度达到O(n)
import java.util.Arrays;
public class BubbleSort {
// 冒泡排序方法
private static void bubble(int[] a) {
// j 表示未排序部分的边界
int j = a.length - 1;
// swapped 标志位,用于判断在一轮遍历中是否发生了交换
boolean swapped;
do {
swapped = false;
// x 用于记录最后一次交换的位置
int x = 0;
// 遍历未排序部分的数组元素
for (int i = 0; i < j; i++) {
// 如果当前元素大于下一个元素,则交换它们
if (a[i] > a[i + 1]) {
int t = a[i];
a[i] = a[i + 1];
a[i + 1] = t;
// 设置标志位为 true,表示发生了交换
swapped = true;
// 更新最后一次交换的位置
x = i;
}
}
// 更新未排序部分的边界为最后一次交换的位置
j = x;
} while (j!= 0 && swapped);
}
public static void main(String[] args) {
// 定义待排序的数组
int[] a = {6, 5, 4, 3, 2, 1};
// 输出排序前的数组
System.out.println(Arrays.toString(a));
// 调用冒泡排序方法
bubble(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
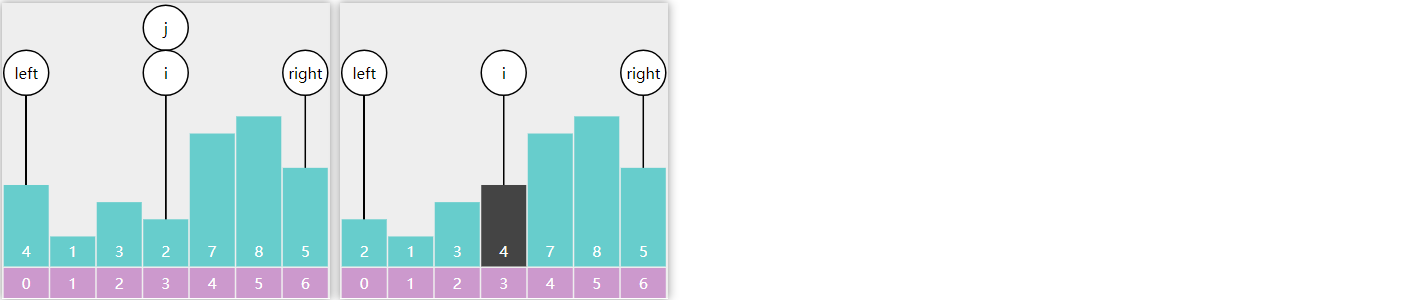
2) 选择排序
要点
- 每一轮选择,找出最大(最小)的元素,并把它交换到合适的位置
以下面的数组选择最大值为例
非递归实现
public class SelectionSort {
// 选择排序方法
public static void sort(int[] a) {
// 1. 选择轮数 a.length - 1
// 2. 交换的索引位置(right) 初始 a.length - 1, 每次递减
for (int right = a.length - 1; right > 0; right--) {
// 假设当前最大元素的索引为 right
int max = right;
// 遍历未排序部分,找到最大元素的索引
for (int i = 0; i < right; i++) {
if (a[i] > a[max]) {
max = i;
}
}
// 如果最大元素不在当前假设位置,进行交换
if (max!= right) {
swap(a, max, right);
}
}
}
// 交换数组中两个索引位置的元素
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {6, 5, 4, 3, 2, 1};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
3) 堆排序
要点:
- 建立大顶堆
- 每次将堆顶元素(最大值)交换到末尾,调整堆顶元素,让它重新符合大顶堆特性
建堆
交换,下潜调整
代码
public class HeapSort {
// 堆排序方法
public static void sort(int[] a) {
// 建堆操作
heapify(a, a.length);
// 从最后一个元素开始,每次将堆顶元素与当前未排序部分的最后一个元素交换,然后对堆顶元素进行下潜操作,以保持堆的性质
for (int right = a.length - 1; right > 0; right--) {
//每次将堆顶元素和最后一个元素交换后,改变right的值,相当于将交换后的最大的值排除在堆之外,其余部分参与下潜
swap(a, 0, right);
down(a, 0, right);
}
}
// 建堆,时间复杂度为 O(n)
private static void heapify(int[] array, int size) {
// 从最后一个非叶子节点开始,对每个非叶子节点进行下潜操作,构建堆
for (int i = size / 2 - 1; i >= 0; i--) {
down(array, i, size);
}
}
// 下潜操作
// 在 LeetCode 上数组排序题目用堆排序求解时,非递归实现比递归实现大约快 6ms
private static void down(int[] array, int parent, int size) {
while (true) {
int left = parent * 2 + 1;
int right = left + 1;
int max = parent;
// 如果左子节点存在且大于当前最大元素,更新最大元素索引为左子节点索引
if (left < size && array[left] > array[max]) {
max = left;
}
// 如果右子节点存在且大于当前最大元素,更新最大元素索引为右子节点索引
if (right < size && array[right] > array[max]) {
max = right;
}
// 如果最大元素就是当前父节点,说明没有找到更大的子节点,退出循环
if (max == parent) {
break;
}
// 交换最大子节点和父节点的元素
swap(array, max, parent);
// 更新父节点索引为最大子节点索引,继续下潜
parent = max;
}
}
// 交换数组中两个索引位置的元素
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {2, 3, 1, 7, 6, 4, 5};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用堆排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
4) 插入排序
要点
- 将数组分为两部分 [0 … low-1] [low … a.length-1]
- 左边 [0 … low-1] 是已排序部分
- 右边 [low … a.length-1] 是未排序部分
- 每次从未排序区域取出 low 位置的元素, 插入到已排序区域
例
代码
public class InsertionSort {
public static void sort(int[] a) {
// low 从 1 开始,因为单个元素的数组本身就是已排序的
for (int low = 1; low < a.length; low++) {
// 将 low 位置的元素暂存起来,准备插入到已排序区域
int t = a[low];
// i 初始为已排序区域的最后一个位置,也就是 low - 1
int i = low - 1;
// 当 i 大于等于 0 且暂存的元素小于当前已排序区域的元素时,继续寻找插入位置
while (i >= 0 && t < a[i]) {
// 将当前已排序区域的元素向后移动一位,为暂存元素空出插入位置
a[i + 1] = a[i];
// i 递减,继续在已排序区域中向前比较
i--;
}
// 找到插入位置,如果 i 不等于 low - 1,说明元素进行了移动
if (i!= low - 1) {
// 将暂存的元素插入到正确位置
a[i + 1] = t;
}
}
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 5, 8, 1, 4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用插入排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
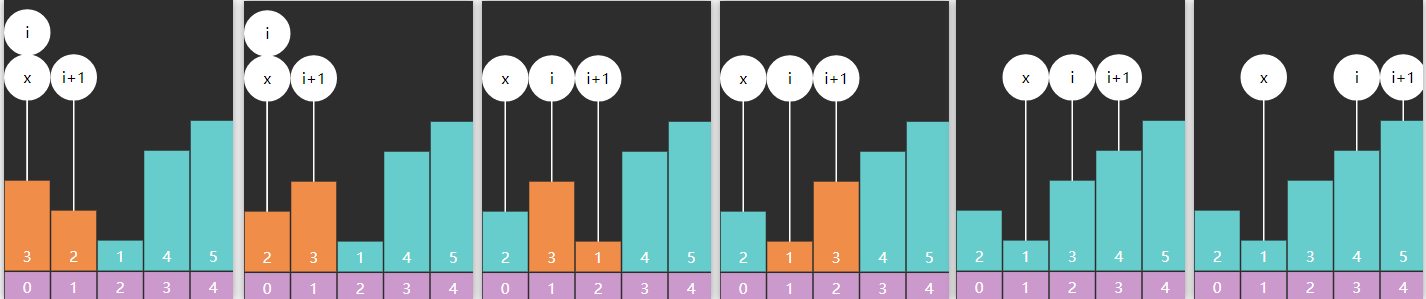
5) 希尔排序
本质上是优化的插入排序
要点
- 简单的说,就是分组实现插入,每组元素间隙称为 gap
- 每轮排序后 gap 逐渐变小,直至 gap 为 1 完成排序
- 对插入排序的优化,让元素更快速地交换到最终位置
下图演示了 gap = 4,gap = 2,gap = 1 的三轮排序前后比较
代码
两层循环,外层循环控制间隙(步长gap),内层循环采取由前到后的方式,每次遍历到一个元素,就和它同一组的前面的元素进行比较并在同一组的元素中进行插入操作,和它同一组的前面的元素已经被排好序,所以每一组遍历到最后一个元素时都是被排好序的。
public class ShellSort {
// 希尔排序方法
public static void sort(int[] a) {
// 外层循环控制步长(gap)逐渐减小
for (int gap = a.length >> 1; gap > 0; gap = gap >> 1) {
// 内层循环对每个子序列进行插入排序
for (int low = gap; low < a.length; low++) {
// 将 low 位置的元素暂存起来,准备插入到已排序区域
int t = a[low];
// i 初始为已排序区域的最后一个位置,也就是 low - gap
int i = low - gap;
// 当 i 大于等于 0 且暂存的元素小于当前已排序区域的元素时,继续寻找插入位置
while (i >= 0 && t < a[i]) {
// 将当前已排序区域的元素向后移动 gap 位,为暂存元素空出插入位置
a[i + gap] = a[i];
// i 递减 gap,继续在已排序区域中向前比较
i -= gap;
}
// 找到插入位置,如果 i 不等于 low - gap,说明元素进行了移动
if (i!= low - gap) {
// 将暂存的元素插入到正确位置
a[i + gap] = t;
}
}
}
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 5, 8, 1, 4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用希尔排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
6) 归并排序
递归实现
要点
- 分 - 每次从中间切一刀,处理的数据少一半
- 治 - 当数据仅剩一个时可以认为有序
- 合 - 两个有序的结果,可以进行合并排序(参见数组练习 E01. 合并有序数组)
代码
自顶至下的方式,通过递的方法,先将数组分成两份,再逐步分散成又两份,直到一份中只有一个元素停止分散,这是认为每一份是有序的。然后通过归的方法,将每对的两份组合在一起,再复制回原来的数组中(此处的组合要求其实是进行一个合并有序数组的工作,需要一个中间数组来储存结果)
public class MergeSortTopDown {
/*
a1 原始数组
i~iEnd 第一个有序范围的起始和结束索引
j~jEnd 第二个有序范围的起始和结束索引
a2 临时数组
*/
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2) {
// 合并两个有序范围到临时数组 a2
int k = i;
while (i <= iEnd && j <= jEnd) {
// 比较两个范围的当前元素,将较小的元素放入 a2
if (a1[i] < a1[j]) {
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
// 如果第一个范围已遍历完,将第二个范围剩余元素复制到 a2
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
}
// 如果第二个范围已遍历完,将第一个范围剩余元素复制到 a2
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
}
}
public static void sort(int[] a1) {
// 进行归并排序,使用临时数组 a2
int[] a2 = new int[a1.length];
split(a1, 0, a1.length - 1, a2);
}
private static void split(int[] a1, int left, int right, int[] a2) {
// 获取当前要处理的子数组
int[] array = Arrays.copyOfRange(a1, left, right + 1);
// System.out.println(Arrays.toString(array));
// 2. 治(当子数组只有一个元素时,直接返回)
if (left == right) {
return;
}
// 1. 分(将子数组分成两部分)
int m = (left + right) >>> 1;
split(a1, left, m, a2); // 递归处理左半部分
split(a1, m + 1, right, a2); // 递归处理右半部分
// 3. 合(合并两个有序的子数组)
merge(a1, left, m, m + 1, right, a2);
// 将合并后的结果复制回原始数组
System.arraycopy(a2, left, a1, left, right - left + 1);
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 8, 5, 1, 4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用归并排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
时间复杂度
-
两个长度为 m 和 n 的链表合并,时间复杂度是 m + n
-
归并,时间复杂度: f ( n ) = 2 f ( n / 2 ) + n , f ( 1 ) = c f(n) = 2f(n/2) + n, f(1)=c f(n)=2f(n/2)+n,f(1)=c,等价解 f ( n ) = n l o g 2 n + c n f(n) = nlog_2{n} + cn f(n)=nlog2n+cn
8 / \ 4 4 / \ / \ 2 2 2 2 || || || || 11 11 11 11 f(8) = 2f(4) + 8 f(4) = 2f(2) + 4 f(2) = 2f(1) + 2 f(1) = 1 f(8) = 8 + 24 f(4) = 4 + 8 f(2) = 2 + 2 f(1) = 1- 当 n = 16 时,结果 80
- 当 n = 64 时,结果 448
-
若逐一合并,时间复杂度: f ( n ) = ∑ n = 0 n − 1 n + 1 f(n)=\sum\limits_{n=0}^{n-1}n+1 f(n)=n=0∑n−1n+1,等价解 f ( n ) = 1 2 ( n 2 + n ) f(n)=\frac{1}{2}(n^2+n) f(n)=21(n2+n)
1|0 => 1 1|1 => 2 1|2 => 3 1|3 => 4 1|4 => 5 1|5 => 6 1|6 => 7 1|7 => 8 36- 当 n = 16 时,结果 136
- 当 n = 64 时,结果 2080
非递归实现
自下至上的方式,从子数组大小为 1 开始逐步递增,每次翻倍,直到子数组大小达到或超过原始数组长度。将子数组大小为1的子数组两两合并后形成子数组大小为2的数组。此时都是有序的,之后子数组大小加倍后再合并,直到合并成一个完整的数组。
public class MergeSortBottomUp {
/*
a1 原始数组
i~iEnd 第一个有序范围
j~jEnd 第二个有序范围
a2 临时数组
*/
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2) {
// 合并两个有序范围到临时数组 a2。
// k 是临时数组 a2 的索引,初始值为 i。
int k = i;
// 当两个范围都还有元素时,进行比较并将较小的元素放入临时数组 a2。
while (i <= iEnd && j <= jEnd) {
if (a1[i] < a1[j]) {
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
// 如果第一个范围已遍历完,将第二个范围剩余元素复制到临时数组 a2。
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
}
// 如果第二个范围已遍历完,将第一个范围剩余元素复制到临时数组 a2。
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
}
}
public static void sort(int[] a1) {
int n = a1.length;
// 创建一个与原始数组 a1 长度相同的临时数组 a2。
int[] a2 = new int[n];
// 从子数组大小为 1 开始逐步递增,每次翻倍,直到子数组大小达到或超过原始数组长度。
for (int width = 1; width < n; width *= 2) {
// 遍历原始数组 a1,以当前子数组大小为步长进行合并操作。
for (int i = 0; i < n; i += 2 * width) {
// 计算第一个子数组的结束索引,确保不超过原始数组长度且不超出当前合并范围。
int m = Integer.min(i + width - 1, n - 1);
// 计算第二个子数组的结束索引,确保不超过原始数组长度且不超出当前合并范围。
int j = Integer.min(i + 2 * width - 1, n - 1);
System.out.println(i + " " + m + " " + j);
// 合并两个子数组,将结果放入临时数组 a2。
merge(a1, i, m, m + 1, j, a2);
}
// 将临时数组 a2 的内容复制回原始数组 a1,完成一轮合并。
System.arraycopy(a2, 0, a1, 0, n);
}
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 8, 5, 1, 4};
// 输出初始数组。
System.out.println(Arrays.toString(a));
// 调用排序方法对数组 a 进行排序。
sort(a);
// 输出排序后的数组。
System.out.println(Arrays.toString(a));
}
}
7) 归并+插入
- 小数据量且有序度高时,插入排序效果高
- 大数据量用归并效果好
- 可以结合二者
设计思路,普通的归并排序是当每一组的元素为1时,才认为该组元素有序,我们结合插入排序的适合小数据量的有点,认为当每一组的数据量小于32时,用插入排序的方式使得该组元素达成有序的目的,再使用归并排序达到并的目的。
public class MergeInsertionSort {
// 插入排序方法,对指定范围内的数组进行插入排序
public static void insertion(int[] a, int left, int right) {
// low 从 left + 1 开始,因为单个元素的数组本身就是已排序的
for (int low = left + 1; low <= right; low++) {
// 将 low 位置的元素暂存起来,准备插入到已排序区域
int t = a[low];
// i 初始为已排序区域的最后一个位置,也就是 low - 1
int i = low - 1;
// 当 i 大于等于 left 且暂存的元素小于当前已排序区域的元素时,继续寻找插入位置
while (i >= left && t < a[i]) {
// 将当前已排序区域的元素向后移动一位,为暂存元素空出插入位置
a[i + 1] = a[i];
// i 递减,继续在已排序区域中向前比较
i--;
}
// 找到插入位置,如果 i 不等于 low - 1,说明元素进行了移动
if (i!= low - 1) {
// 将暂存的元素插入到正确位置
a[i + 1] = t;
}
}
}
/*
a1 原始数组
i~iEnd 第一个有序范围
j~jEnd 第二个有序范围
a2 临时数组
*/
public static void merge(int[] a1, int i, int iEnd, int j, int jEnd, int[] a2) {
// 合并两个有序范围到临时数组 a2
int k = i;
while (i <= iEnd && j <= jEnd) {
// 比较两个范围的当前元素,将较小的元素放入 a2
if (a1[i] < a1[j]) {
a2[k] = a1[i];
i++;
} else {
a2[k] = a1[j];
j++;
}
k++;
}
// 如果第一个范围已遍历完,将第二个范围剩余元素复制到 a2
if (i > iEnd) {
System.arraycopy(a1, j, a2, k, jEnd - j + 1);
}
// 如果第二个范围已遍历完,将第一个范围剩余元素复制到 a2
if (j > jEnd) {
System.arraycopy(a1, i, a2, k, iEnd - i + 1);
}
}
public static void sort(int[] a1) {
// 创建临时数组 a2
int[] a2 = new int[a1.length];
// 调用分割方法进行排序
split(a1, 0, a1.length - 1, a2);
}
private static void split(int[] a1, int left, int right, int[] a2) {
// int[] array = Arrays.copyOfRange(a1, left, right + 1);
// System.out.println(Arrays.toString(array));
// 2. 治(当子数组只有一个元素时,直接返回)
if (right == left) {
return;
}
// 如果子数组长度小于等于 32,使用插入排序
if (right - left <= 32) {
insertion(a1, left, right);
System.out.println("insert..." + left + " " + right + " " + Arrays.toString(a1));
return;
}
// 1. 分(将子数组分成两部分)
int m = (left + right) >>> 1;
split(a1, left, m, a2); // 递归处理左半部分
split(a1, m + 1, right, a2); // 递归处理右半部分
System.out.println(left + " " + right + " " + Arrays.toString(a1));
// 3. 合(合并两个有序的子数组)
merge(a1, left, m, m + 1, right, a2);
// 将合并后的结果复制回原始数组
System.arraycopy(a2, left, a1, left, right - left + 1);
}
public static void main(String[] args) {
int[] a = {9, 3, 7, 2, 8, 5, 1, 4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
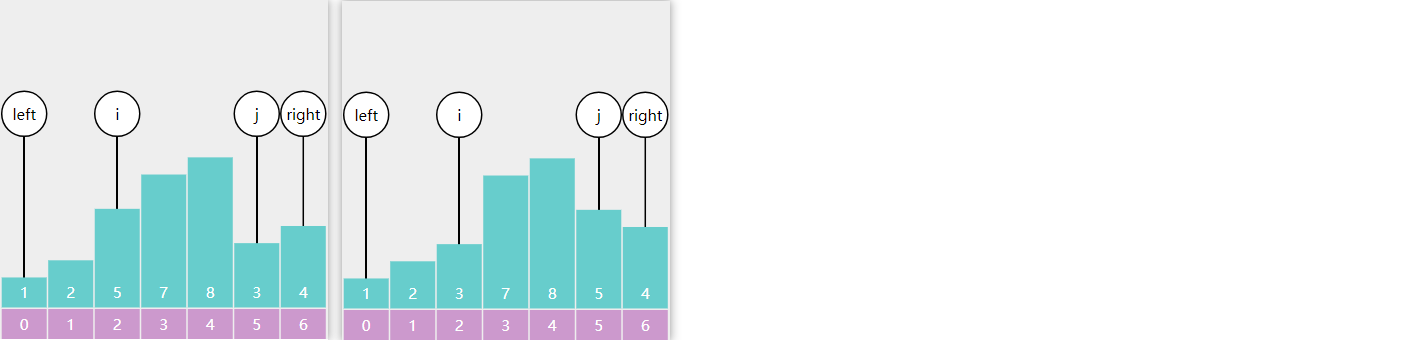
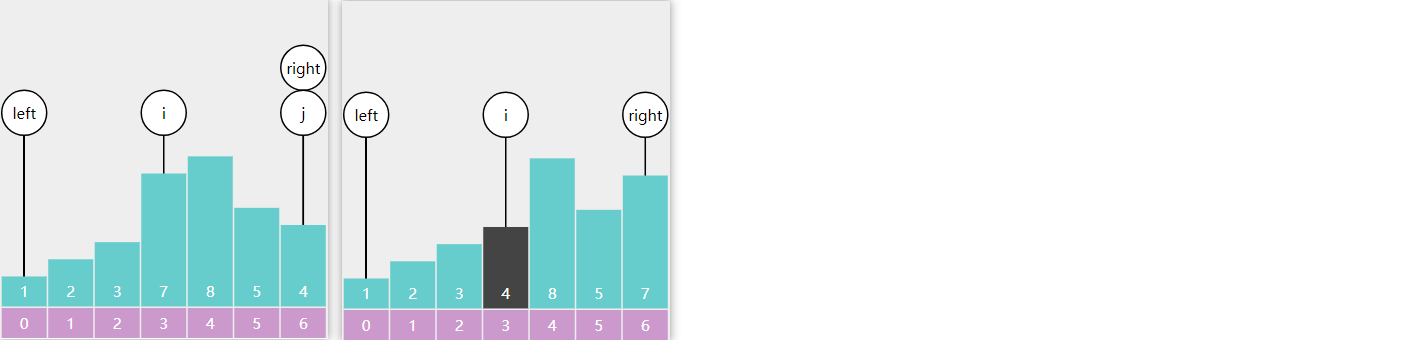
8) 快速排序
单边排序和双边排序我都采取了以右边界为基准点的方式,便于记忆
单边循环(lomuto分区)要点
- 选择最右侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- 交换时机:j 找到小的,且与 i 不相等
- i 找到 >= 基准点元素后,不应自增(此处在代码位置有详细讲解)
- 最后基准点与 i 交换,i 即为基准点最终索引(i指向比基准点大的元素)
例:
i 和 j 都从左边出发向右查找,i 找到比基准点4大的5,j找到比基准点小的2,停下来交换
i 找到了比基准点大的5,j 找到比基准点小的3,停下来交换
j 到达right 处结束,right 与 i 交换,一轮分区结束
代码
- i和j同时向前遍历,直到找到一个比基准点大的值,i不动,j向后遍历直到找到一个比基准点小的值,i和j同时++。此时i++后i处的值到j处的范围内的值肯定比基准点的值大,因为此处已经被j遍历过,一种情况是此处的值比基准点大且未被交换过,一种情况是i和j相差为1,此处的值是刚刚交换过来的i处原来的比基准点大的值。
- 当j小于基准点,i的值会有两种情况
- i == j此时说明i处的值没有出现过比基准点大的情况,i++
- i!= j 此时说明出现过i的值比基准点大的情况,交换后i++,此时i++后i处的值到j处的范围内的值肯定比基准点的值大,因为此处已经被j遍历过,一种情况是此处的值比基准点大且未被交换过,一种情况是i和j相差为1,此处的值是刚刚交换过来的i处原来的比基准点大的值。
- 最后一步当i处的值和基准点的值进行交换时,有两种情况
- 从来没有发生过i和j处的值的交换,说明基准点左侧的值都比基准点小,此时i指向基准点,交换没有影响
- 发生过i和j处的交换,此时i处指向的值到j指向的值的范围内一定是比基准点大的值,i处是从左到右第一个比基准点大的值。
public class QuickSortLomuto {
// 快速排序入口方法
public static void sort(int[] a) {
// 调用快速排序的递归方法,对整个数组进行排序
quick(a, 0, a.length - 1);
}
private static void quick(int[] a, int left, int right) {
// 如果左边界大于等于右边界,说明子数组只有一个元素或为空,直接返回
if (left >= right) {
return;
}
// 进行分区操作,返回基准点元素的索引
int p = partition(a, left, right);
// 对基准点左边的子数组进行快速排序
quick(a, left, p - 1);
// 对基准点右边的子数组进行快速排序
quick(a, p + 1, right);
}
private static int partition(int[] a, int left, int right) {
// 选取最右边的元素作为基准点元素值
int pv = a[right];
// i 表示小于基准点元素值的区间的右边界(即现状态从左到右第一个比基准点大的元素)
int i = left;
// j 用于遍历数组
int j = left;
while (j < right) {
// 如果当前元素小于基准点元素值
if (a[j] < pv) {
// 如果 i 不等于 j,说明找到了小于基准点的元素且不在正确位置,进行交换
if (i!= j) {
swap(a, i, j);
}
// 扩大小于基准点元素值的区间
i++;
}
// 继续遍历下一个元素
j++;
}
// 将基准点元素放到正确的位置(i 所指位置)
swap(a, i, right);
// 返回基准点元素的索引
return i;
}
private static void swap(int[] a, int i, int j) {
// 交换数组中两个位置的元素
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {5, 3, 7, 2, 9, 8, 1, 4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用快速排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
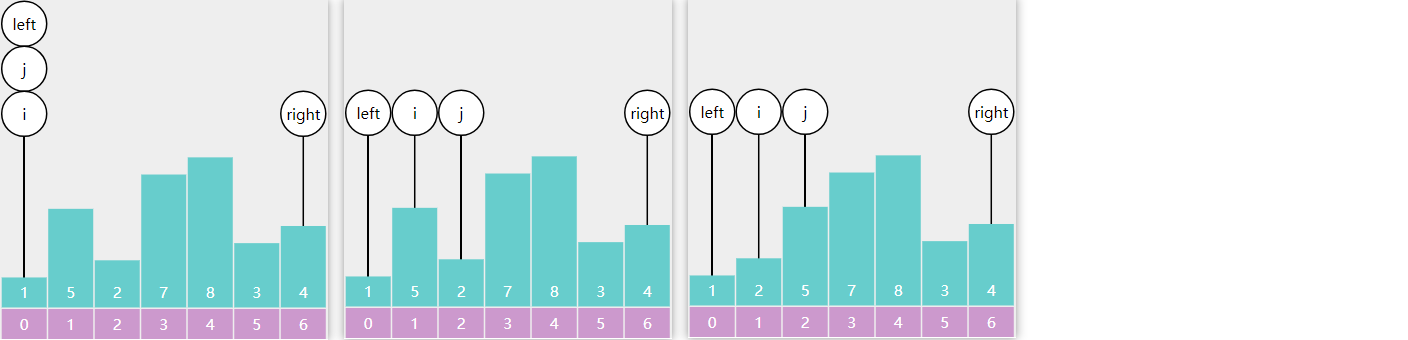
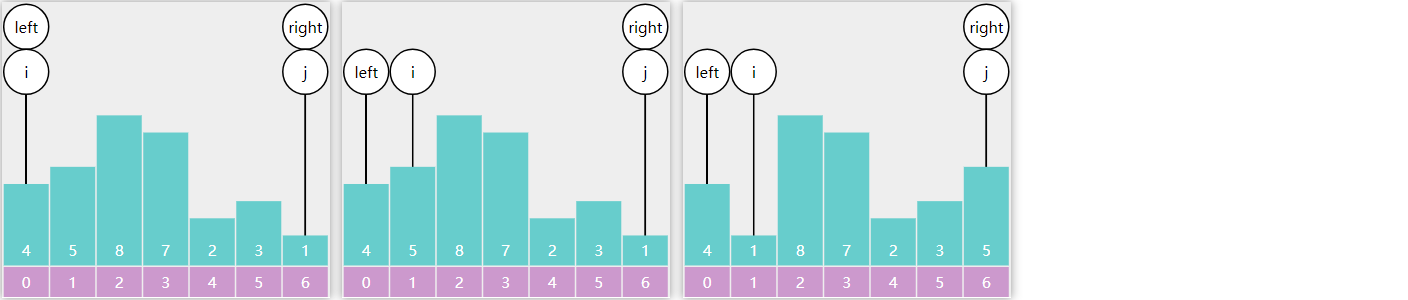
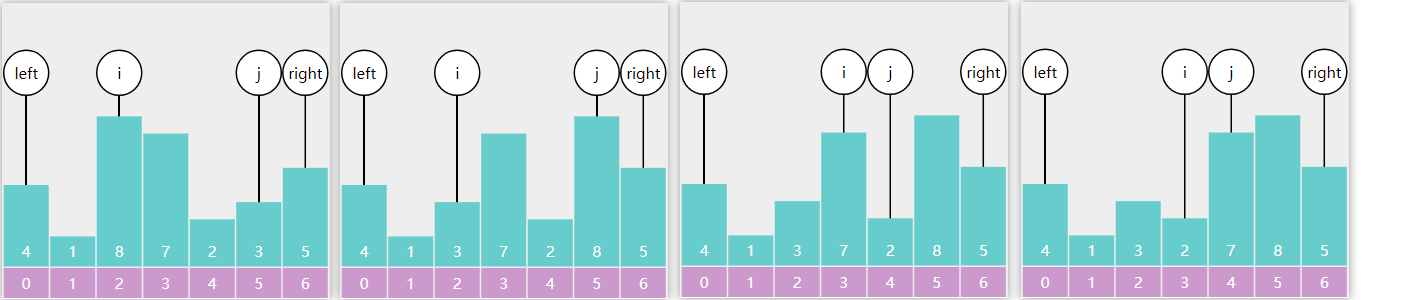
双边循环要点
- 选择最左侧元素作为基准点
- j 找比基准点小的,i 找比基准点大的,一旦找到,二者进行交换
- i 从左向右
- j 从右向左
- 最后基准点与 i 交换,i 即为基准点最终索引
例:
i 找到比基准点大的5停下来,j 找到比基准点小的1停下来(包含等于),二者交换
i 找到8,j 找到3,二者交换,i 找到7,j 找到2,二者交换
i == j,退出循环,基准点与 i 交换
代码
i和j循环的顺序不能随便改动,因为我们是要取最右侧的元素为基准点,最后一步是用i处的值和基准点的值进行交换,所以我们要优先让i去找比基准点大的值。假设这样一种场景,i和j交换后,i处的值比基准点小,j处的值比基准点大,i和j相邻,如果j优先—,那么i处的值将比基准点小,却需要和基准点交换。
import java.util.Arrays;
public class QuickSortHoare {
// 快速排序的入口方法,对给定数组进行排序
public static void sort(int[] a) {
// 调用快速排序的递归方法,传入数组的起始索引和结束索引
quick(a, 0, a.length - 1);
}
// 快速排序的递归方法
private static void quick(int[] a, int left, int right) {
// 如果左边界大于等于右边界,说明子数组只有一个元素或为空,直接返回
if (left >= right) {
return;
}
// 对当前子数组进行分区操作,得到基准点的索引
int p = partition(a, left, right);
// 对基准点左边的子数组进行快速排序
quick(a, left, p - 1);
// 对基准点右边的子数组进行快速排序
quick(a, p + 1, right);
}
// 分区方法,将数组分为两部分,左边部分小于基准点,右边部分大于基准点
private static int partition(int[] a, int left, int right) {
// i 表示左指针,初始指向左边界
int i = left;
// j 表示右指针,初始指向右边界
int j = right;
// 选取右边界的元素作为基准点元素值
int pv = a[right];
while (i < j) {
// 从左往右找第一个大于基准点的元素(注意,如果找不到比基准点大的元素,i < j也不会成立,不会发生swap)
while (i < j && a[i] <= pv) {
i++;
}
// 从右往左找第一个小于基准点的元素(这里的=是避免一直在基准点处循环,基准点的值就是j处的值)
while (i < j && a[j] >= pv) {
j--;
}
// 如果找到了满足条件的 i 和 j,交换它们所指的元素
if (i < j) {
swap(a, i, j);
}
}
// 将基准点元素放到正确的位置(i 所指位置)
swap(a, right, i);
// 返回基准点元素的索引
return i;
}
// 交换数组中两个位置的元素
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {9,7,5,8,4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用快速排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
随机基准点
使用随机数作为基准点,避免万一最大值或最小值作为基准点导致的分区不均衡
例
改进代码
int idx = ThreadLocalRandom.current().nextInt(right - left + 1) + left;//基准点随机
swap(a, idx, right);//交换随机基准点和数组最后一个值,将其设为基准点
package cn.itcast.demo;
import java.util.Arrays;
import java.util.concurrent.ThreadLocalRandom;
public class QuickSortHoare {
// 快速排序的入口方法,对给定数组进行排序
public static void sort(int[] a) {
// 调用快速排序的递归方法,传入数组的起始索引和结束索引
quick(a, 0, a.length - 1);
}
// 快速排序的递归方法
private static void quick(int[] a, int left, int right) {
// 如果左边界大于等于右边界,说明子数组只有一个元素或为空,直接返回
if (left >= right) {
return;
}
// 对当前子数组进行分区操作,得到基准点的索引
int p = partition(a, left, right);
// 对基准点左边的子数组进行快速排序
quick(a, left, p - 1);
// 对基准点右边的子数组进行快速排序
quick(a, p + 1, right);
}
// 分区方法,将数组分为两部分,左边部分小于基准点,右边部分大于基准点
private static int partition(int[] a, int left, int right) {
int idx = ThreadLocalRandom.current().nextInt(right - left + 1) + left;//基准点随机
swap(a, idx, right);//交换随机基准点和数组最后一个值,将其设为基准点
// i 表示左指针,初始指向左边界
int i = left;
// j 表示右指针,初始指向右边界
int j = right;
// 选取右边界的元素作为基准点元素值
int pv = a[right];
while (i < j) {
// 从左往右找第一个大于基准点的元素
// 从右往左找第一个小于基准点的元素
while (i < j && a[j] >= pv) {
j--;
}
while (i < j && a[i] <= pv) {
i++;
}
// 如果找到了满足条件的 i 和 j,交换它们所指的元素
if (i < j) {
swap(a, i, j);
}
}
// 将基准点元素放到正确的位置(i 所指位置)
swap(a, right, i);
// 返回基准点元素的索引
return i;
}
// 交换数组中两个位置的元素
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {9,7,5,8,4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用快速排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
处理重复值
如果重复值较多,则原来算法中的分区效果也不好,如下图中左侧所示,需要想办法改为右侧的分区效果
改进代码
package cn.itcast.demo;
import java.util.Arrays;
public class QuickSortHoare {
// 快速排序的入口方法,对给定数组进行排序
public static void sort(int[] a) {
// 调用快速排序的递归方法,传入数组的起始索引和结束索引
quick(a, 0, a.length - 1);
}
// 快速排序的递归方法
private static void quick(int[] a, int left, int right) {
// 如果左边界大于等于右边界,说明子数组只有一个元素或为空,直接返回
if (left >= right) {
return;
}
// 对当前子数组进行分区操作,得到基准点的索引
int p = partition(a, left, right);
// 对基准点左边的子数组进行快速排序
quick(a, left, p - 1);
// 对基准点右边的子数组进行快速排序
quick(a, p + 1, right);
}
// 分区方法,将数组分为两部分,左边部分小于基准点,右边部分大于基准点
private static int partition(int[] a, int left, int right) {
// i 表示左指针,初始指向左边界
int i = left;
// j 表示右指针,初始指向右边界
int j = right - 1;
// 选取右边界的元素作为基准点元素值
int pv = a[right];
while (i <= j) {
// 从左往右找第一个大于等于基准点的元素(注意,如果找不到比基准点大的元素,i < j也不会成立,不会发生swap)
while (i <= j && a[i] < pv) {
i++;
}
// 从右往左找第一个小于等于基准点的元素(这里的=是避免一直在基准点处循环,基准点的值就是j处的值)
while (i <= j && a[j] > pv) {
j--;
}
// 如果找到了满足条件的 i 和 j,交换它们所指的元素
if (i <= j) {
swap(a, i, j);
i++;
j--;
//这里如果不加i++和j--的话,遇到所有值一样的情况,会循环进行交换
}
}
// 将基准点元素放到正确的位置(i 所指位置)
swap(a, right, i);
// 返回基准点元素的索引
return i;
}
// 交换数组中两个位置的元素
private static void swap(int[] a, int i, int j) {
int t = a[i];
a[i] = a[j];
a[j] = t;
}
public static void main(String[] args) {
int[] a = {2,1,3,2,4};
// 输出初始数组
System.out.println(Arrays.toString(a));
// 调用快速排序方法
sort(a);
// 输出排序后的数组
System.out.println(Arrays.toString(a));
}
}
-
核心思想是
- 改进前,i 只找大于的,j 会找小于等于的。一个不找等于、一个找等于,势必导致等于的值分布不平衡
- 改进后,二者都会找等于的交换,等于的值会平衡分布在基准点两边
-
细节:
- 因为一开始 i 就可能等于 j,因此外层循环需要加等于条件保证至少进入一次,让 j 能减到正确位置
- 内层 while 循环中 i <= j 的 = 也不能去掉,因为 i == j 时也要做一次与基准点的判断,好让 i 及 j 正确
- i == j 时,也要做一次 i++ 和 j-- 使下次循环二者不等才能退出
- 因为最后退出循环时 i 会大于 j,因此最终与基准点交换的是 i
-
内层两个 while 循环的先后顺序不再重要
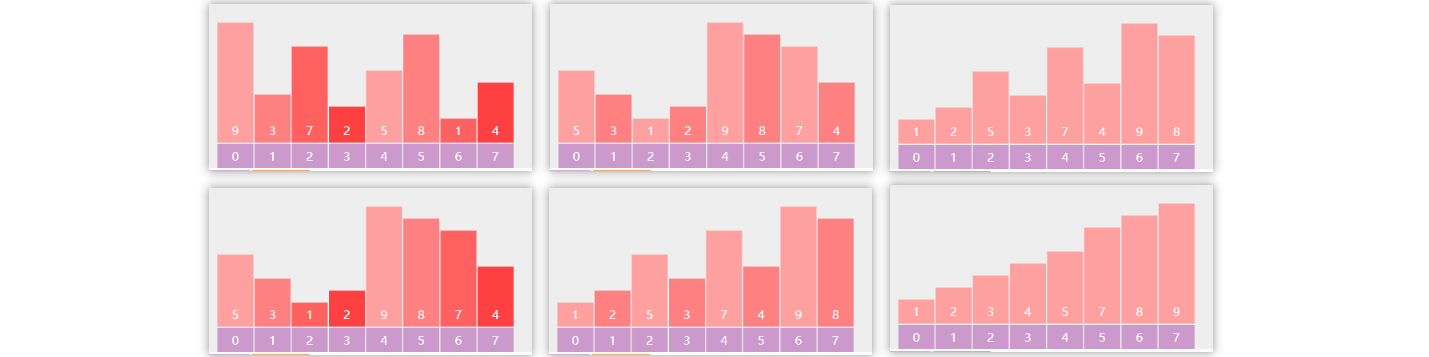
9) 计数排序
方法1(简化后的计数排序)
记录好每个元素的个数,通过寻找min值和max的值确定计数数组的大小的偏移量,参考哈希表的思路,然后遍历计数数组从小到大输出达到排序的目的。
public static void sort(int[] a) {
// 找到数组中的最小值和最大值
int min = a[0];
int max = a[0];
for (int i : a) {
if (i > max) {
max = i;
} else if (i < min) {
min = i;
}
}
// 创建计数数组,大小为最大值减去最小值加一
int[] counting = new int[max - min + 1];
// 遍历原数组,统计每个元素出现的次数
for (int i : a) {
counting[i - min]++;
}
// 将计数数组中的元素按顺序填充回原数组
int k = 0;
for (int i = 0; i < counting.length; i++) {
while (counting[i] > 0) {
a[k] = i + min;
counting[i]--;
k++;
}
}
}
针对 byte [],因为数据范围已知,省去了求最大、最小值的过程,java 中对 char[]、short[]、byte[] 的排序都可能采用 counting 排序
// 针对 byte 类型数组的计数排序,省去求最大最小值过程(因为 byte 范围已知)
public static void sort(byte[] a) {
// 创建计数数组,大小为 256(byte 的取值范围是 -128 到 127)
int[] counting = new int[256];
for (int i : a) {
// 确保索引在 0 到 255 范围内
counting[i & 0xFF]++;
}
int k = a.length - 1;
// 从较大索引开始遍历计数数组
for (int i = 128 + 256; k >= 0;) {
// 找到第一个非零计数的索引
while (counting[--i & 0xFF] == 0);
int v = i & 0xFF;
int c = counting[i & 0xFF];
// 将对应数量的元素填充回原数组
for (int j = 0; j < c; j++) {
a[k] = (byte) v;
k--;
}
}
}
稳定计数排序
实现了稳定性,调整了计数数组,在原来的计数数组的基础上由前到后相加,是的每个位置上存储的是小于等于|当前索引对应的元素|的元素个数,之后从原数组末尾开始遍历,每遍历一个元素,根据对应的计数数组的元素的值放入temp数组中,再将对应的计数数组元素-1,下一次遍历到这个元素时就会放在上一次遍历的元素的前边,达到稳定性
// 稳定计数排序(适用于一般整数数组)
public static void sort2(int[] a) {
// 找到数组中的最小值和最大值
int min = a[0];
int max = a[0];
for (int i : a) {
if (i > max) {
max = i;
} else if (i < min) {
min = i;
}
}
// 创建计数数组,大小为最大值减去最小值加一
int[] counting = new int[max - min + 1];
// 遍历原数组,统计每个元素出现的次数
for (int i : a) {
counting[i - min]++;
}
// 调整计数数组,使得每个位置存储小于等于当前索引的元素总数
for (int i = 1; i < counting.length; i++) {
counting[i] = counting[i] + counting[i - 1];
}
// 创建临时数组用于存储排序后的结果
int[] b = new int[a.length];
// 从原数组末尾开始遍历,保证稳定性
for (int i = a.length - 1; i >= 0; i--) {
int j = a[i] - min;
counting[j]--;
// 将元素放入临时数组的正确位置
b[counting[j]] = a[i];
}
// 将临时数组的内容复制回原数组
System.arraycopy(b, 0, a, 0, a.length);
}
}
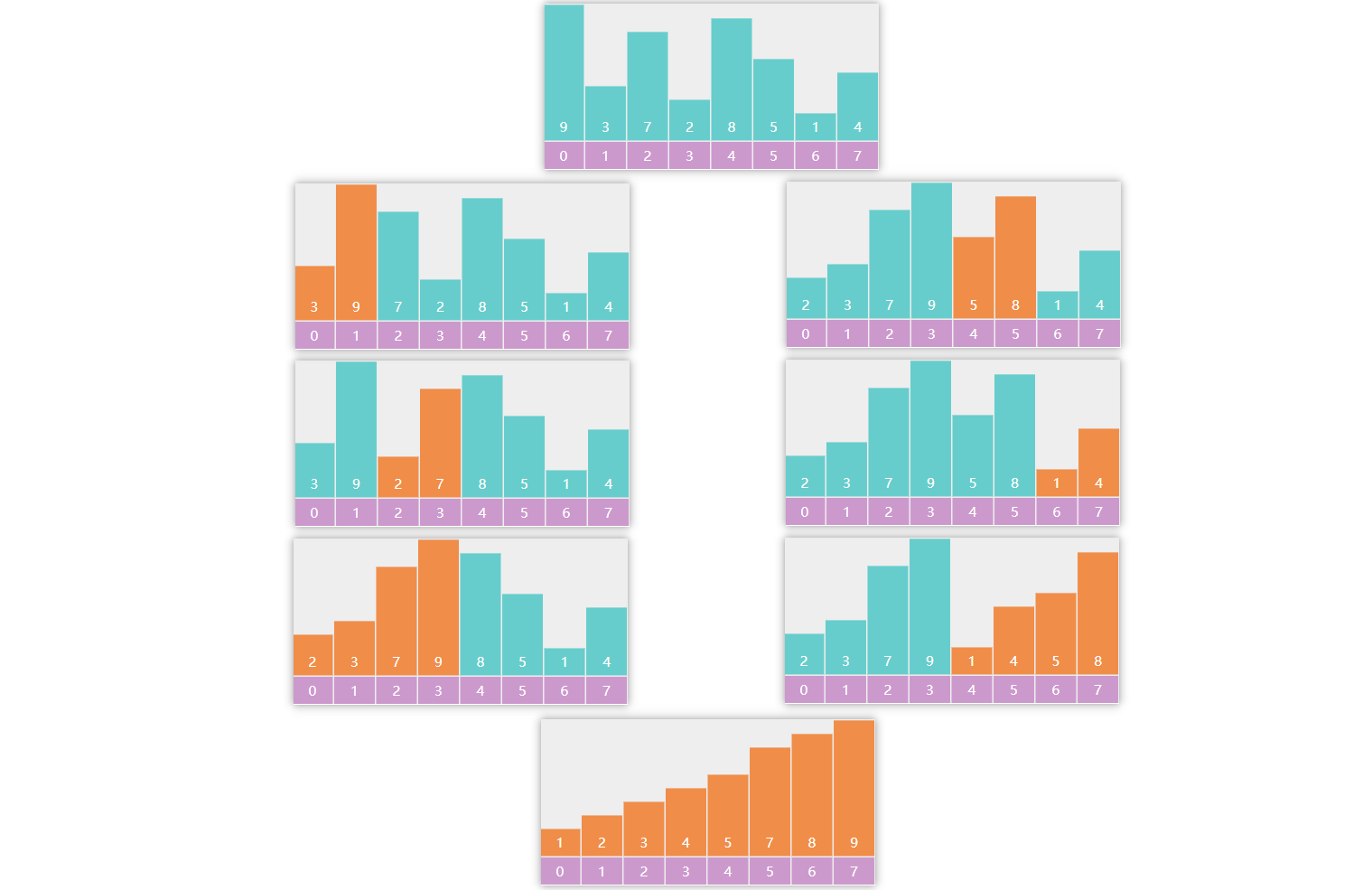
10) 桶排序
将数组中的元素分为若干桶(组),每个桶是一个范围的数组,桶之间有顺序关系,将桶中的元素排好序之后再按照桶的顺序进行合并
初步实现
import java.util.ArrayList;
import java.util.Arrays;
class InsertionSort {
// 插入排序方法,用于对给定的整数数组进行排序
public static void sort(int[] a) {
int n = a.length;
for (int i = 1; i < n; i++) {
int key = a[i];
int j = i - 1;
// 将当前元素与前面已排序的部分进行比较和插入
while (j >= 0 && a[j] > key) {
a[j + 1] = a[j];
j--;
}
a[j + 1] = key;
}
}
}
public class BucketSort {
public static void main(String[] args) {
int[] ages = {20, 18, 66, 25, 67, 30};
// 输出初始数组
System.out.println(Arrays.toString(ages));
// 调用排序方法
sort(ages);
// 输出排序后的数组
System.out.println(Arrays.toString(ages));
}
public static void sort(int[] a) {
// 使用 ArrayList 数组作为桶,每个桶代表一个特定范围的元素集合
ArrayList<Integer>[] buckets = new ArrayList[10];
for (int i = 0; i < buckets.length; i++) {
// 初始化每个桶为一个新的 ArrayList
buckets[i] = new ArrayList<>();
}
for (int v : a) {
// 根据元素的值除以 10 确定桶的索引,将元素添加到对应的桶中
ArrayList<Integer> bucket = buckets[v / 10];
bucket.add(v);
}
int k = 0;
for (ArrayList<Integer> bucket : buckets) {
// 将桶中的元素转换为整数数组
int[] array = bucket.stream().mapToInt(Integer::intValue).toArray();
// 对桶中的元素进行插入排序
InsertionSort.sort(array);
for (int v : array) {
// 将排序后的桶中的元素放回原数组
a[k++] = v;
}
}
}
}
优化:
上面的方法将桶的范围设置为固定的,如过所有元素都在一个桶中,那么桶排序就没有意义,桶的个数和自定义每个桶的范围大小和元素的范围有关
import java.util.ArrayList;
import java.util.Arrays;
class InsertionSort {
// 插入排序方法,用于对给定的整数数组进行排序
public static void sort(int[] a) {
int n = a.length;
// 从第二个元素开始遍历数组
for (int i = 1; i < n; i++) {
int key = a[i];
int j = i - 1;
// 将当前元素与前面已排序的部分进行比较和插入
while (j >= 0 && a[j] > key) {
a[j + 1] = a[j];
j--;
}
a[j + 1] = key;
}
}
}
public class BucketSortGeneric {
public static void main(String[] args) {
int[] ages = {20, 10, 28, 66, 25, 31, 67, 30, 70};
// 输出初始数组
System.out.println("初始数组:" + Arrays.toString(ages));
// 调用排序方法,传入数组和范围参数
sort(ages, 20);
// 输出排序后的数组
System.out.println("排序后的数组:" + Arrays.toString(ages));
}
public static void sort(int[] a, int range) {
int max = a[0];
int min = a[0];
// 找到数组中的最大值和最小值
for (int i = 1; i < a.length; i++) {
if (a[i] > max) {
max = a[i];
}
if (a[i] < min) {
min = a[i];
}
}
// 1. 准备桶
// 根据范围计算桶的数量,并创建桶列表数组
ArrayList<Integer>[] buckets = new ArrayList[(max - min) / range + 1];
for (int i = 0; i < buckets.length; i++) {
buckets[i] = new ArrayList<>();
}
// 2. 放入年龄数据
// 将每个年龄值分配到对应的桶中
for (int age : a) {
buckets[(age - min) / range].add(age);
}
int k = 0;
for (ArrayList<Integer> bucket : buckets) {
// 3. 排序桶内元素
// 获取桶中的元素列表,并转换为整数数组进行插入排序
int[] array = bucket.stream().mapToInt(Integer::intValue).toArray();
InsertionSort.sort(array);
System.out.println("桶内排序后的数组:" + Arrays.toString(array));
// 4. 把每个桶排序好的内容,依次放入原始数组
// 将排序后的桶中的元素放回原数组
for (int v : array) {
a[k++] = v;
}
}
}
}
11) 基数排序
对每一位进行桶排序,适合数据量较大的情况,此时采用桶排序或者计数排序需要的计数数组或者桶数组过大
import java.util.ArrayList;
import java.util.Arrays;
public class RadixSort {
// 基数排序方法,对字符串数组进行排序
public static void radixSort(String[] a, int length) {
// 创建 128 个桶,因为 ASCII 码值范围是 0-127
ArrayList<String>[] buckets = new ArrayList[128];
for (int i = 0; i < buckets.length; i++) {
// 初始化每个桶为一个新的 ArrayList
buckets[i] = new ArrayList<>();
}
// 从字符串的最后一位开始,逐位进行分配和收集
for (int i = length - 1; i >= 0; i--) {
// 将每个字符串分配到对应的桶中
for (String s : a) {
// 根据字符串当前位的字符的 ASCII 值确定桶的索引
buckets[s.charAt(i)].add(s);
}
int k = 0;
// 遍历每个桶,将桶中的字符串收集回原数组
for (ArrayList<String> bucket : buckets) {
for (String s : bucket) {
a[k++] = s;
}
// 清空桶,为下一轮分配做准备
bucket.clear();
}
}
}
public static void main(String[] args) {
String[] phoneNumbers = new String[10];
phoneNumbers[0] = "138";
phoneNumbers[1] = "139";
phoneNumbers[2] = "136";
phoneNumbers[3] = "137";
phoneNumbers[4] = "135";
phoneNumbers[5] = "134";
phoneNumbers[6] = "150";
phoneNumbers[7] = "151";
phoneNumbers[8] = "152";
phoneNumbers[9] = "157";
// 调用基数排序方法,传入字符串数组和字符串长度(这里是 3,因为电话号码示例只取了前三位)
RadixSort.radixSort(phoneNumbers, 3);
// 输出排序后的字符串数组
for (String phoneNumber : phoneNumbers) {
System.out.println(phoneNumber);
}
}
}
基数排序是稳定排序,因此先排个位、再排十位,十位的排序不会打乱个位取值相等的元素顺序