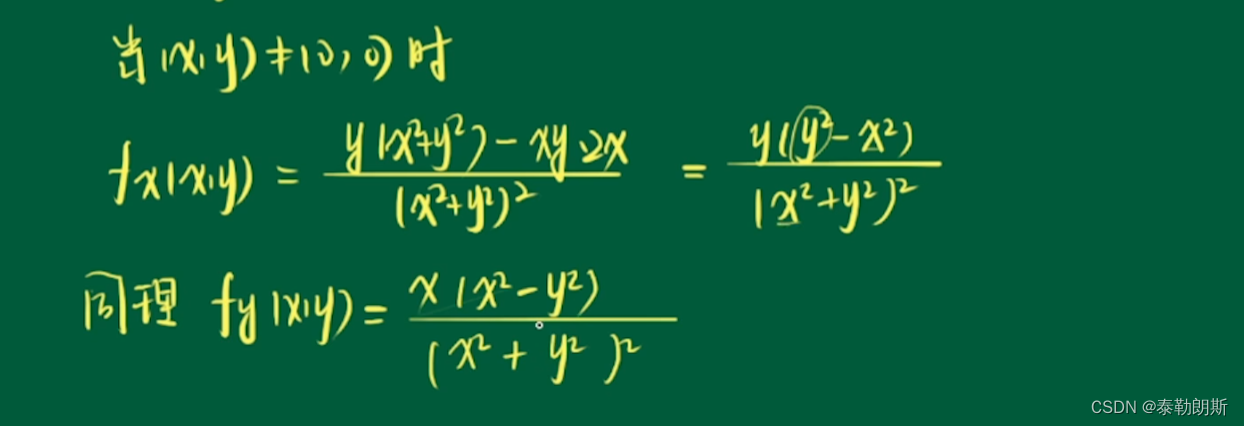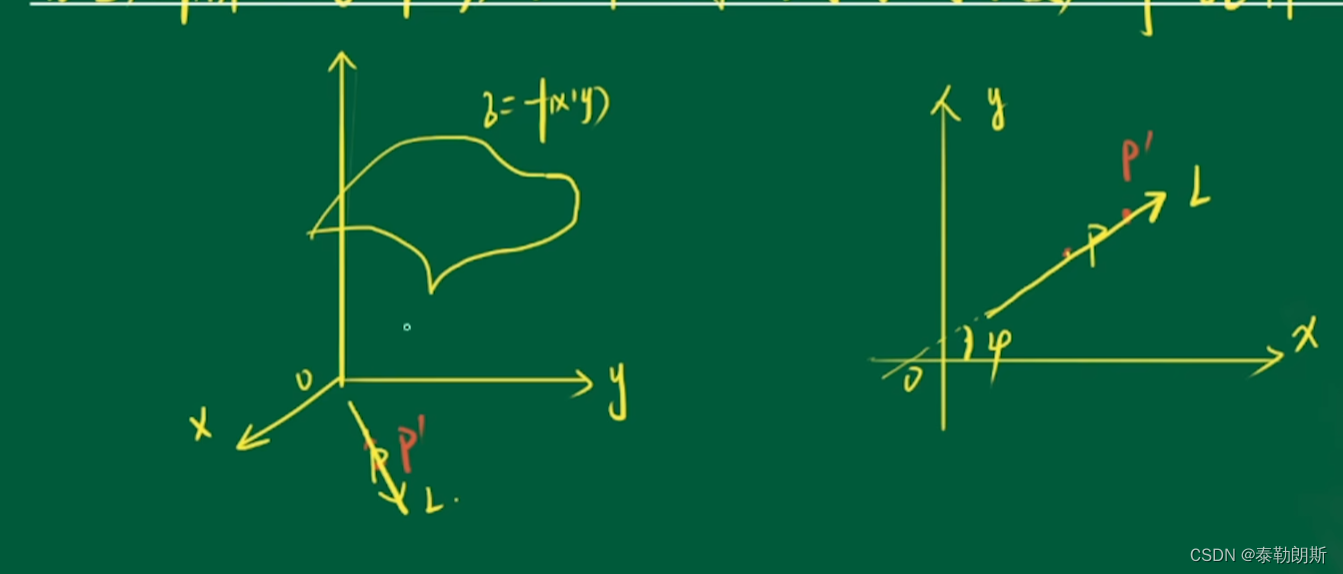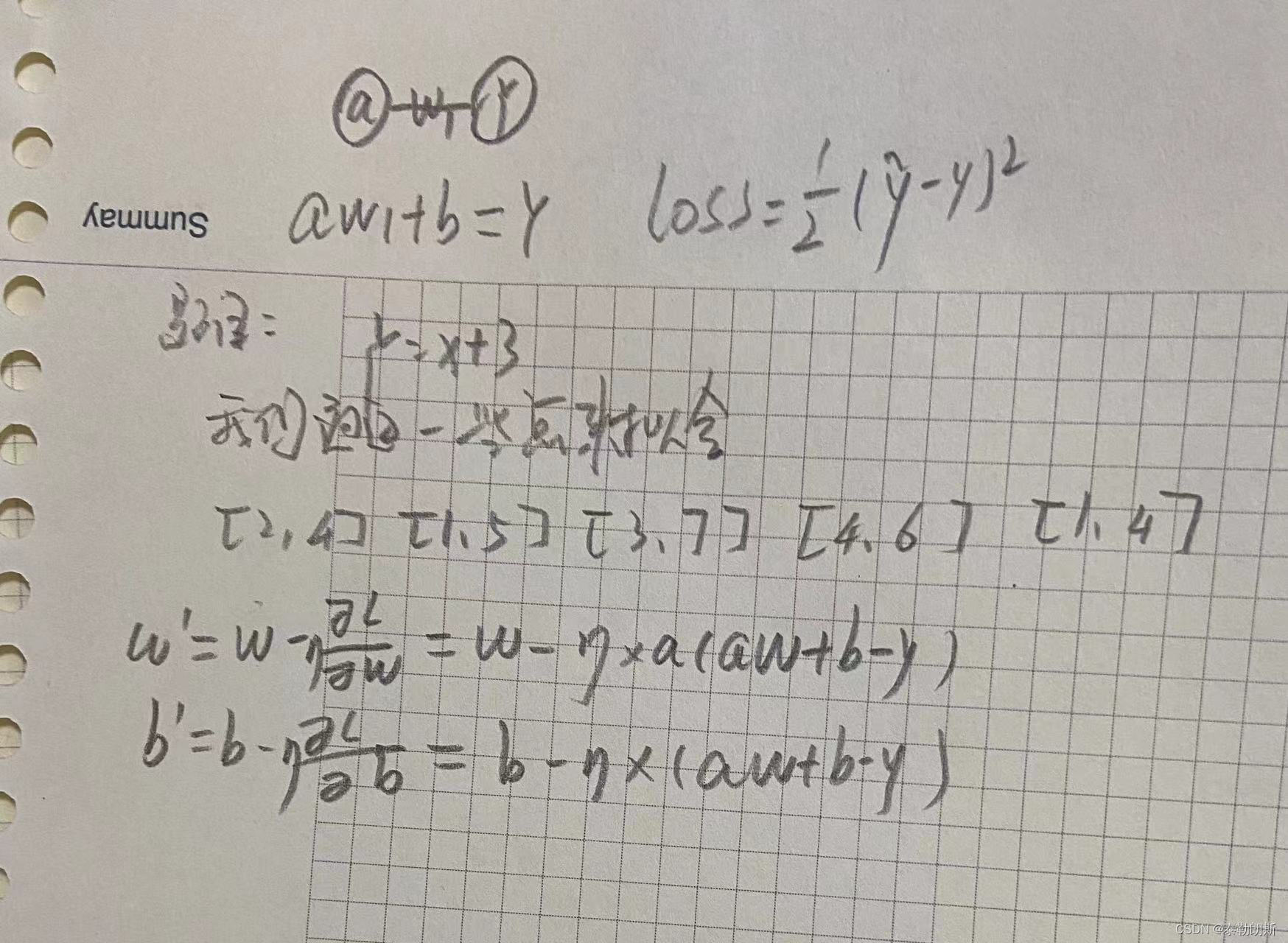前言

为了更好的理解梯度下降，重新看了一下梯度下降的高数课长，现在根据学习内容，把课件贴图，防止哪一天自己记不起来。

下面的内容是通过B站视频整理而来。

高数学习

1.偏导数

偏导数是一个整体，不能拆开

2.偏导数概念

1.对x的偏导数

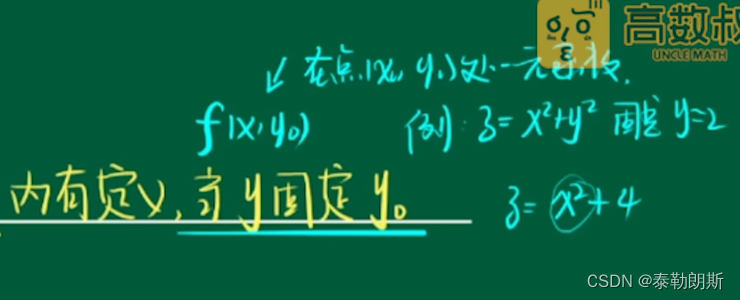
2.对y的偏导数

3.多元函数偏导数

4.如何计算偏导数

1.二元函数的偏导数

2.复杂函数的偏导数

3.分段函数

1.分界点的偏导数

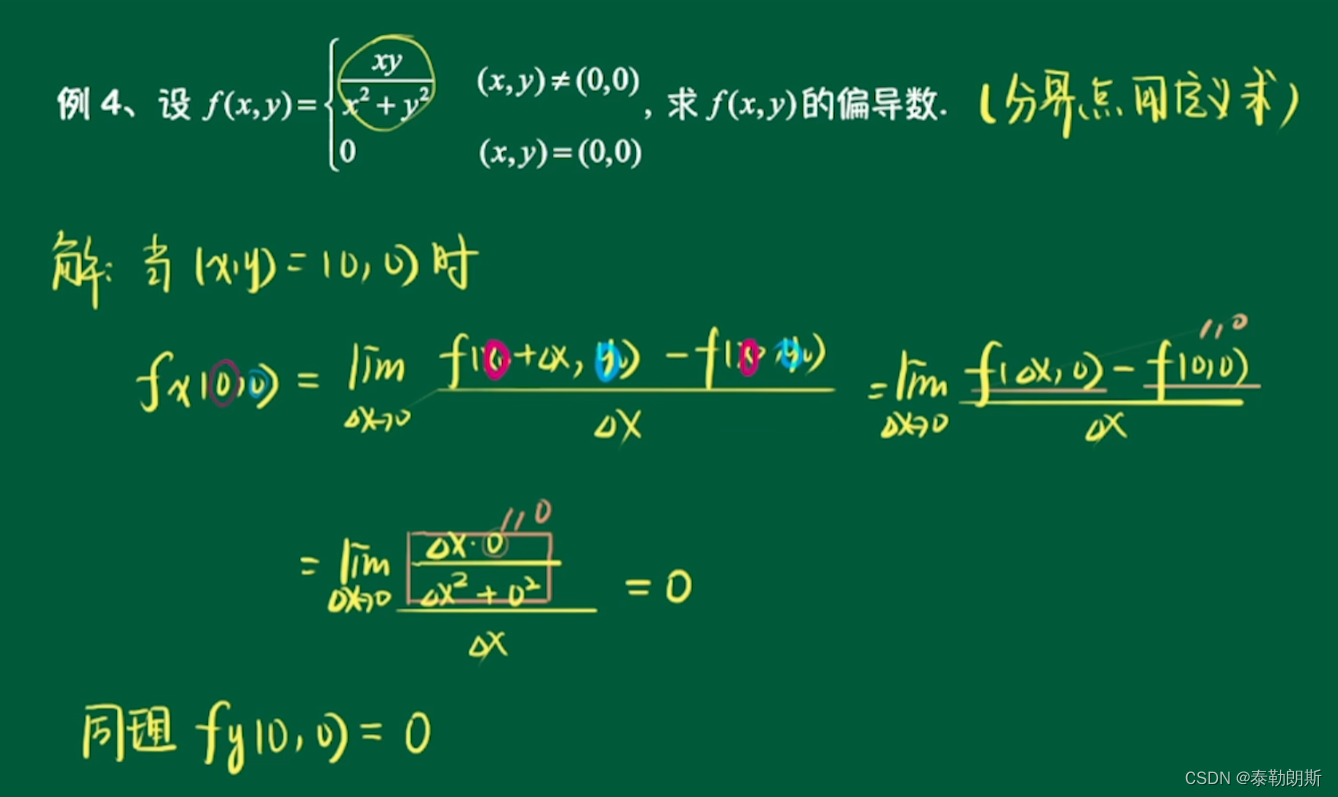
因为x,y是对称函数，所以它们俩的偏导数是相同的。

。

5.偏导数与连续之间的关系

沿着不同方向趋近于0，那么y=kx
二元函数，偏导数存在，不能证明二元函数连续

6.偏导数的几何意义

偏导数是正交的

7.高阶偏导数

1.定义

2.高阶偏导数例题（二阶偏导数）

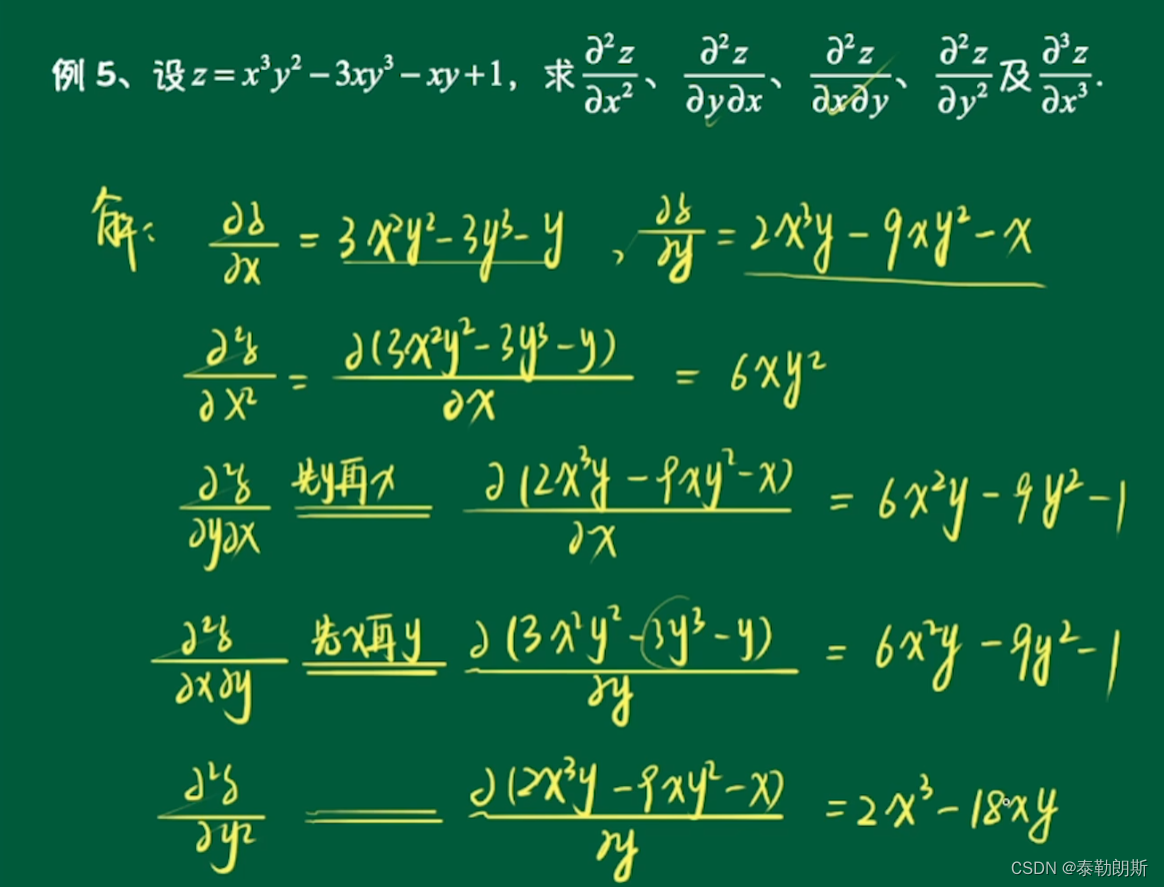
3.全微分

A,和B是和x,y有关的量

1.偏增量定义

2.全增量定义

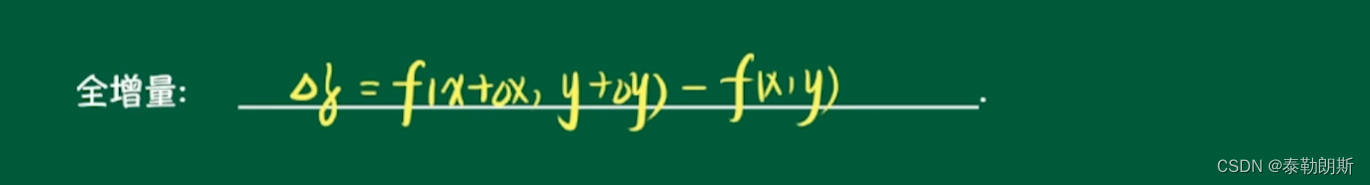
3计算方式

4.多元函数微分学的几何应用

1.定义

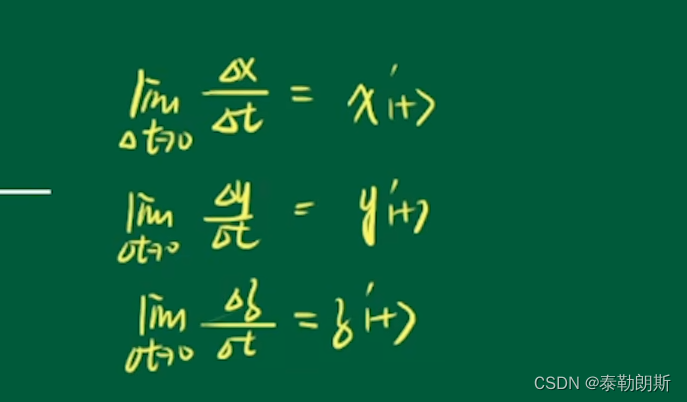
最后求出切线的方程

<img src=https://img-blog.csdnimg.cn/603f8d6256c54b3abb60d39f710506c4.png" width=800>

曲线的切向量
法平面

2.例题1

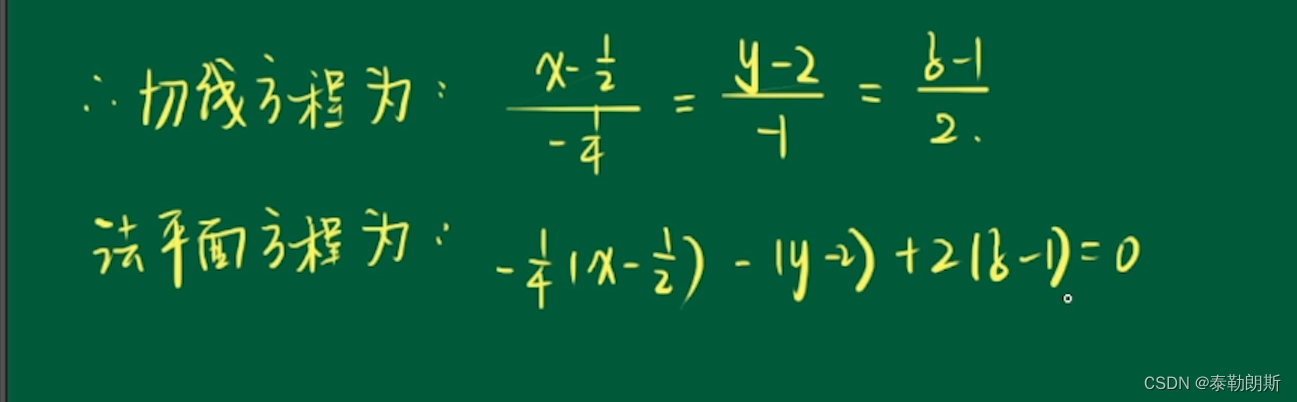
5.方向导数

1.方向导数定义

说明平面是连续的

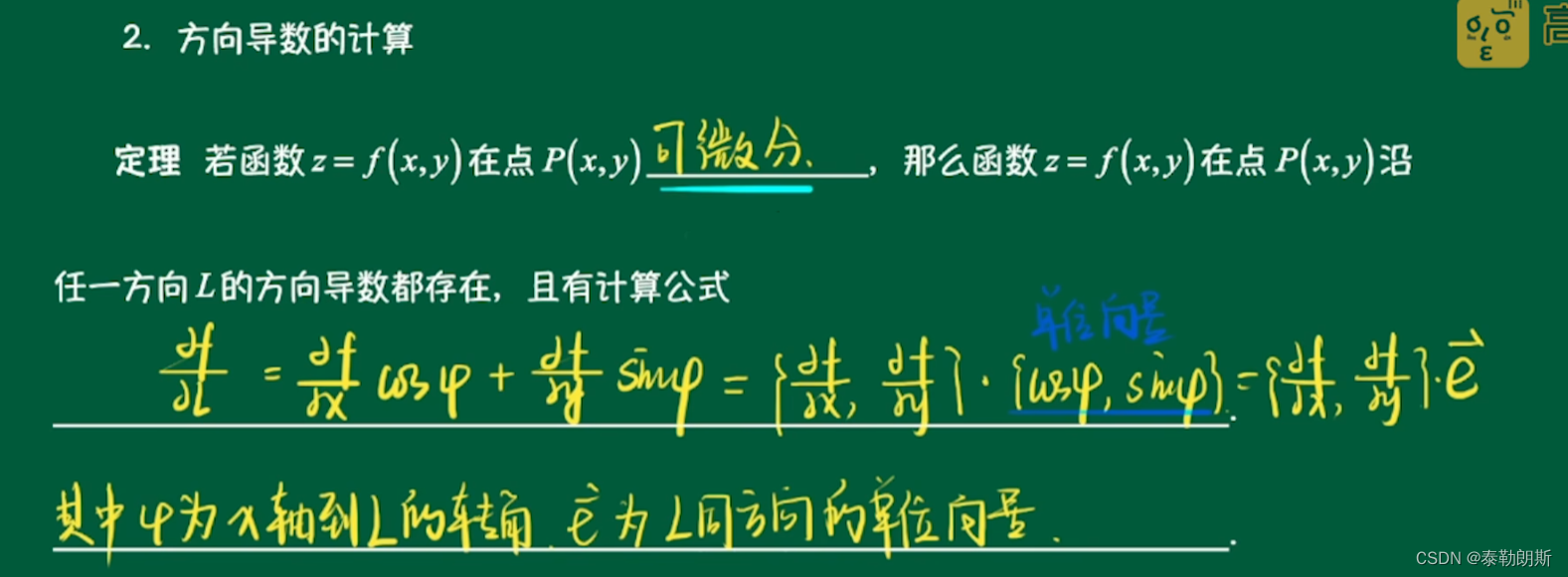
2.方向导数的计算

导数就是斜率，方向导数就是某个点平面的斜率值

方向导数是关于角度的函数，因为偏导数已经确定了

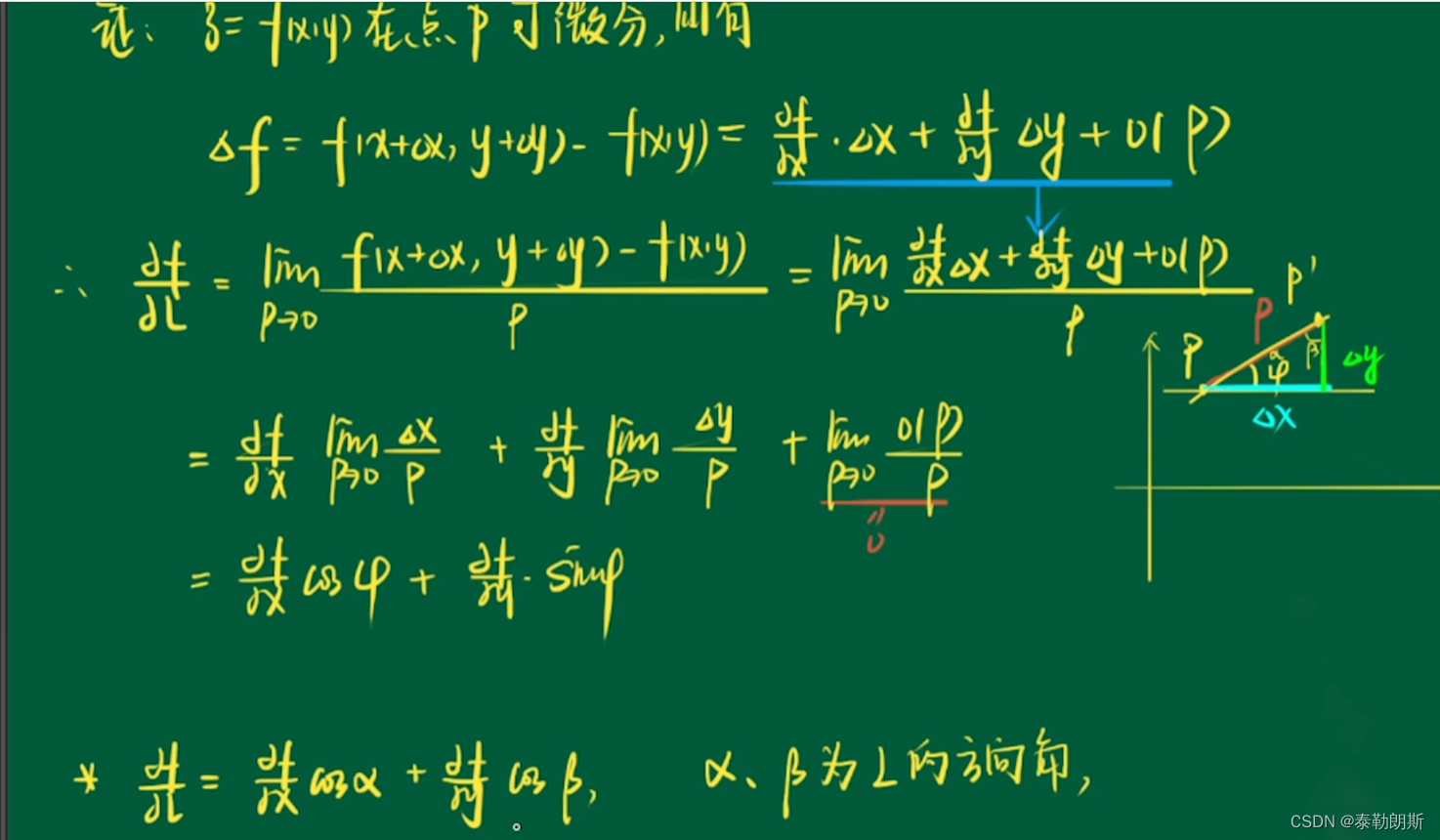
3. 方向导数和偏导数的关系

方向导数存在，偏导数就存在，反之则不一定
方向导数是偏导数的推广

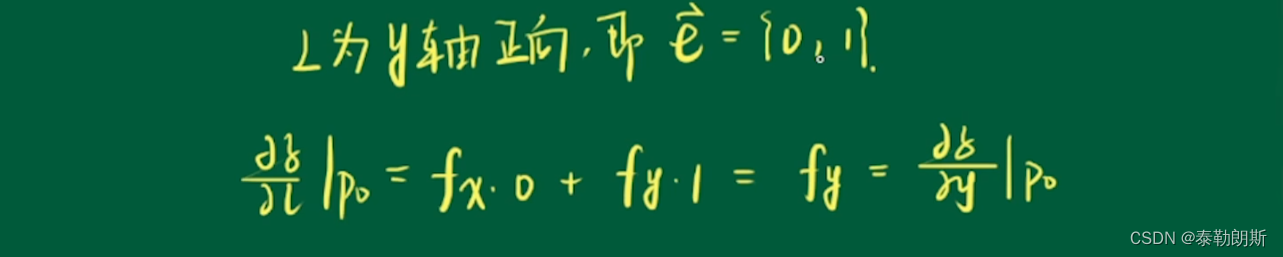
4.方向导数计算

1.例题1

1.例题2

5.三元函数的方向导数

1.定义

2.例题1

3.例题2

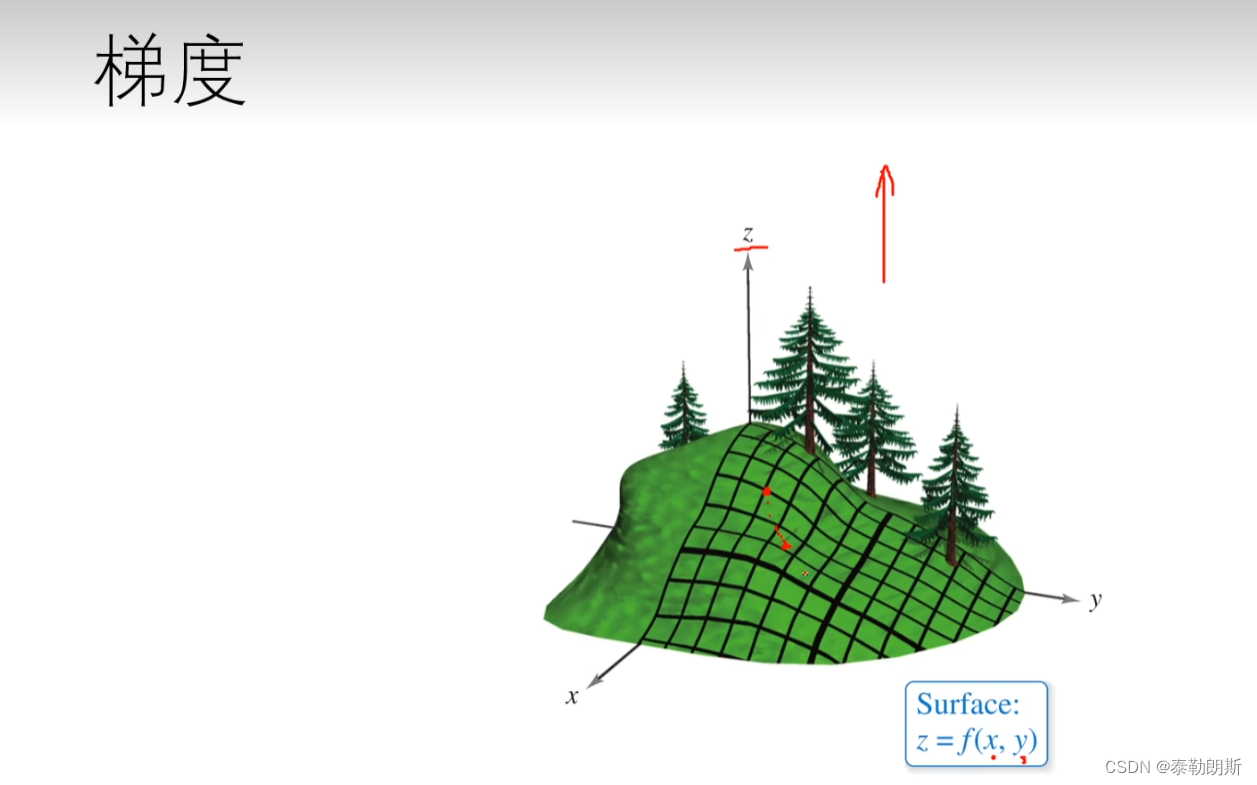
6.梯度

1.定义-梯度就是沿着这个方向，方向导数能达到最大值

单位向量，是指模等于1的向量

单位向量有无数个

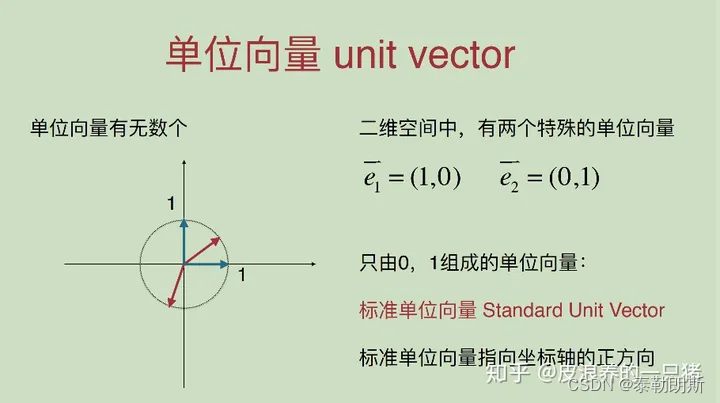
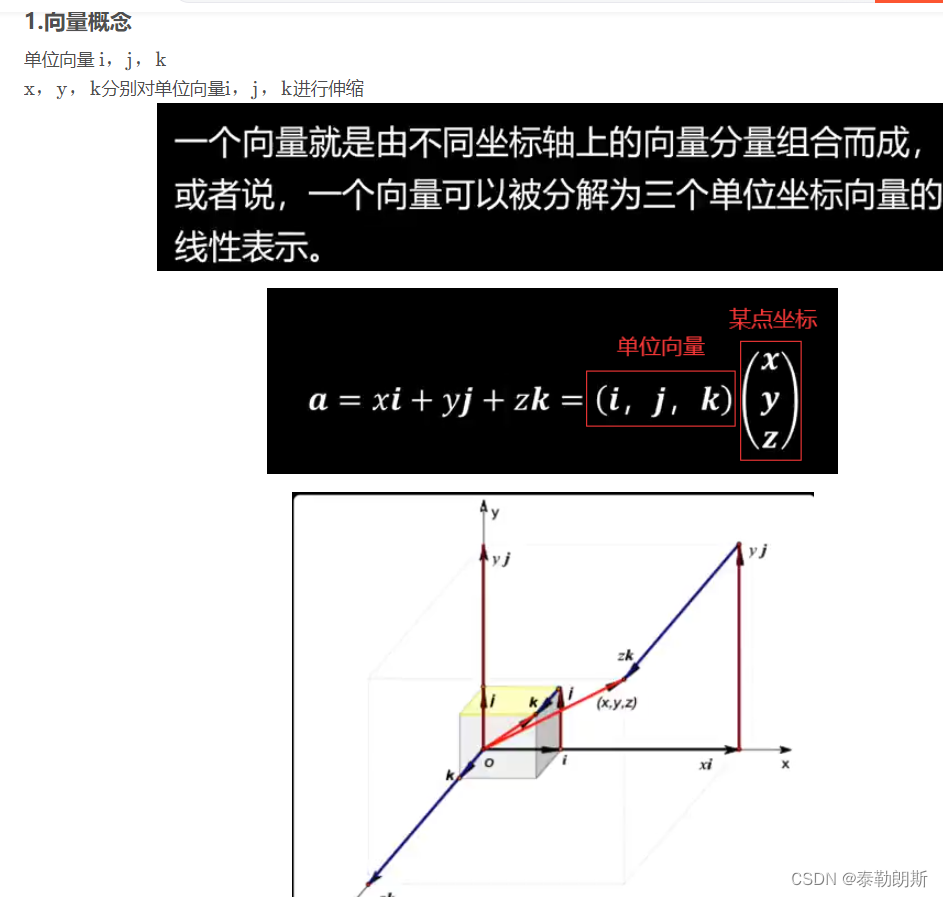
梯度就是沿着这个方向，方向导数能达到最大值

2.方向导数和梯度的关系

1.向量内积

2.向量数量积

3.梯度与方向导数

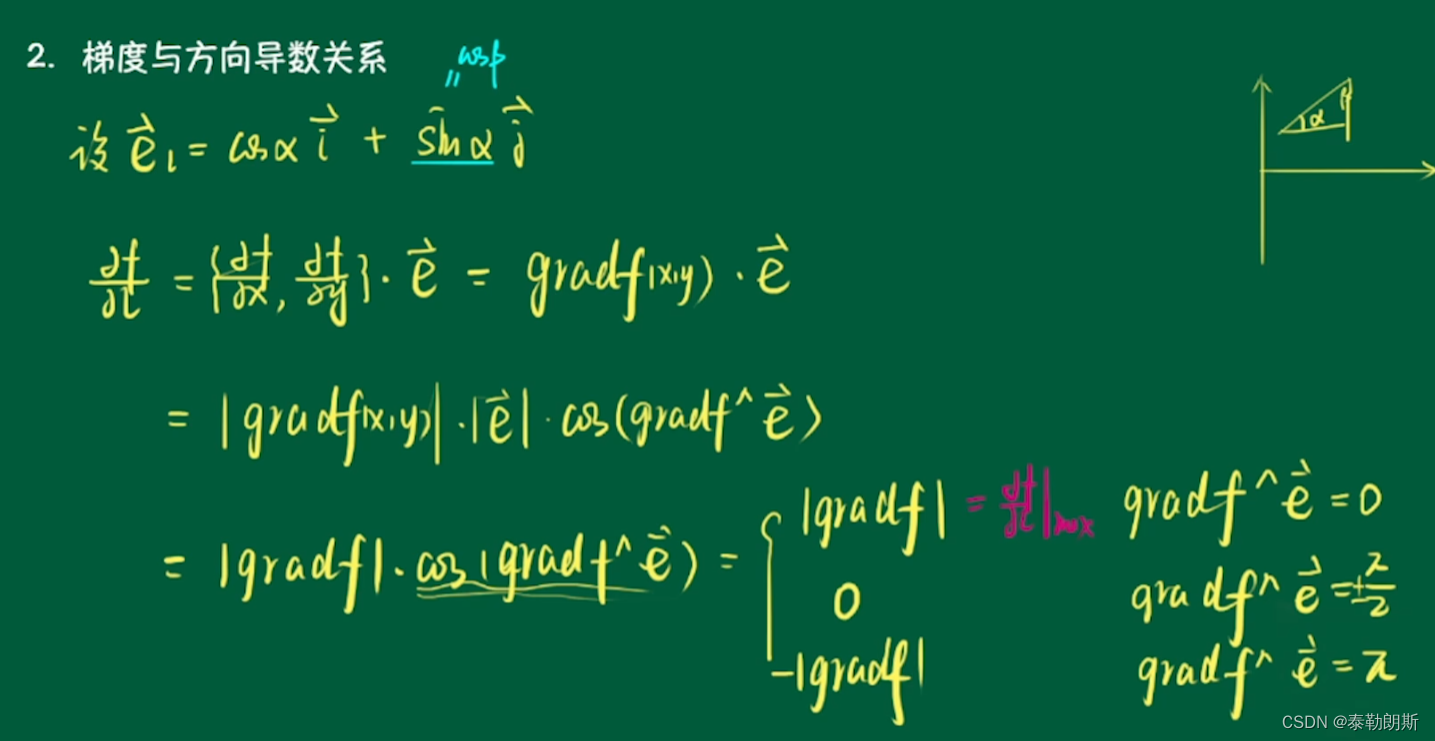
4.梯度总结

5.梯度的角度

6.梯度的计算-1

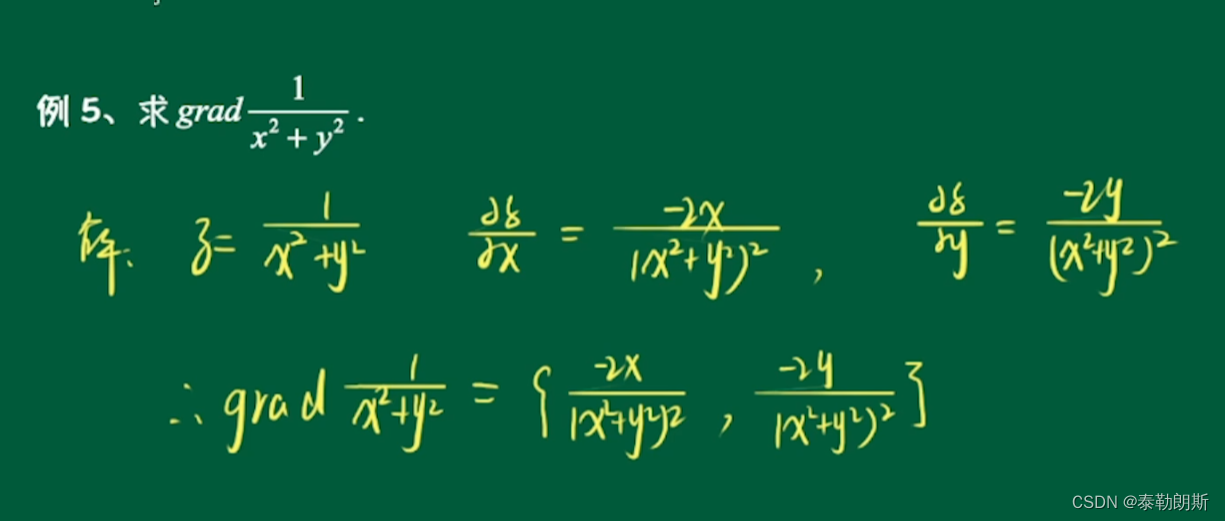
7.梯度的计算-2

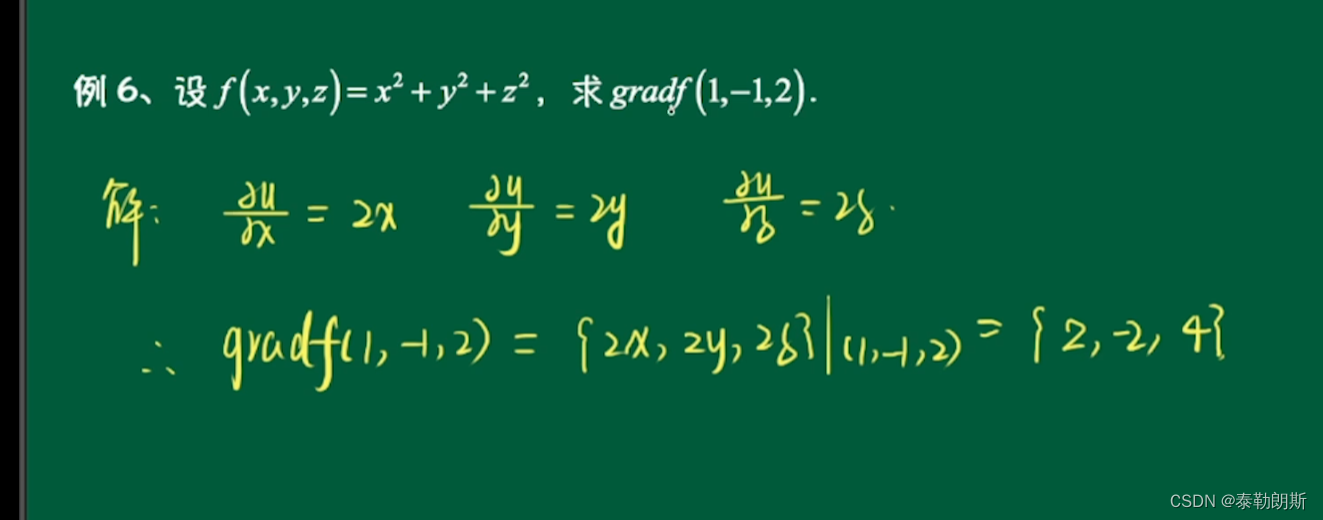
8.梯度的计算-3

7 梯度下降

、

import os

w=2
b=2

n=0.1

array=[[2,4],[1,5],[3,7],[4,6],[1,4],[2,5],[3,6]]

for j in range(5):
    for i in range(len(array)):
        a=array[i][0]
        y=array[i][1]
        w1=w-n*a*(a*w+b-y)
        b1=b-n*(a*w+b-y)
        w=w1
        b=b1

print(w,b)