一、数组的定义以及运算
1、数组是一种数据类型。从逻辑结构上看,数组可以看成是一般线性表的扩充。二维数组可以看成是线性表的线性表。例如:
2、我们可以把二维数组看成一个线性表:
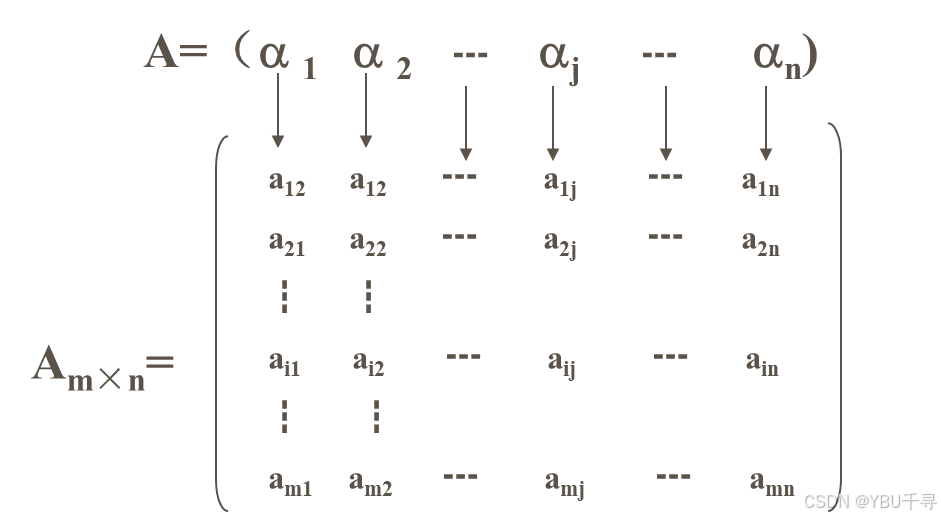
A=(a 1 a 2 … aj … an),其中aj(1≤j ≤n)本身也是一个线性表,称为列向量。
矩阵Am×n看成n个列向量的线性表,即aj=(a1j,a2j, …,amj)
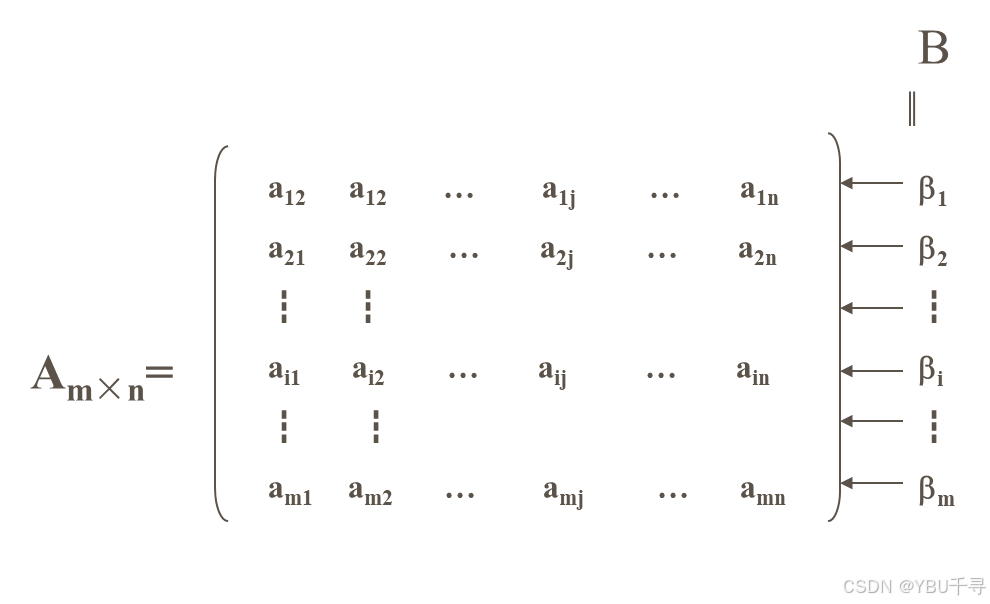
相同的原理,我们还可以将数组Am×n看成另外一个线性表:
B=(b1,,b2,,… ,bm),其中bi(1≤i ≤m)本身也是一个线性表,称为行向量,即: βI= (ai1,ai2, …,aij ,…,ain)。
上面二维数组的例子,介绍了数组的结构特性,实际上数组是一组有固定个数的元素的集合。由于这个性质,使得对数组的操作不象对线性表的操作那样,可以在表中任意一个合法的位置插入或删除一个元素。
3、对于数组的基本操作:
(1)InitArray(A,n,bound1,…,boundn): 若维数n和各维的长度合法,则构造相应的数组A,并返回TRUE;
(2)DestroyArray(A): 销毁数组A;
(3)GetValue(A,e, index1, …,indexn): 若下标合法,用e返回数组A中由index1, …,indexn所指定的元素的值。
(4)SetValue(A,e,index1, …,indexn): 若下标合法,则将数组A中由index1, …,indexn所指定的元素的值置为e。
一定要注意:这里定义的数组下标是从1开始,与C语言的数组略有不同。
4、数组的抽象数据类型定义(ADT Array)
数据对象:D={ aj1j2…jn| n>0,称为数组的维数,ji是数组的第i维下标,1≤ji≤bi,bi为数组第i维的长度, aj1j2…jn ∈ElementSet}
数据关系:R={R1,R2,…,Rn}
Ri={< aj1 … ji…jn ,aj1 … ji+1…jn > | 1≤jk≤bk,1≤k≤n 且k≠i,1≤ji≤bi-1, aj1 … ji…jn ,aj1 … ji+1…jn ∈D,i=1,…,n}
二、数组的顺序存储和实现
对于数组A,一旦给定其维数n及各维长度bi(1≤i≤n),则该数组中元素的个数是固定的,不可以对数组做插入和删除操作,不涉及移动元素操作,因此对于数组而言,采用顺序存储法比较合适。
数组的顺序存储结构有两种:一种是按行序存储,如高级语言BASIC、COBOL和PASCAL语言都是以行序为主。另一种是按列序存储,如高级语言中的FORTRAN语言就是以列序为主。
对于二维数组Amxn
以行为主的存储序列为:a11 ,a12, … a1n ,a21 ,a22 ,…,a2n , … … ,am1 ,am2 , …, amn
以列为主存储序列为:a11, a21,… am1 ,a12 ,a22 ,… ,am2 ,… … ,a1n ,a2n , … ,amn
以二维数组Amn为例,假设每个元素只占一个存储单元,“以行为主”存放数组,下标从1开始,首元素a11的地址为Loc[1,1] 求任意元素aij的地址 ,可由如下计算公式得到:
Loc[i,j]=Loc[1,1]+n×(i-1)+(j-1)
如果每个元素占size个存储单元 ,则任意元素aij的地址计算公式为:
Loc[i,j]=Loc[1,1] + (n×(i-1)+j-1)×size
三维数组A(1..r , 1..m , 1..n)可以看成是r个m×n的二维数组 ,如下图所示:
假定每个元素占一个存储单元,采用以行为主序的方法存放 ,首元素ai11的地址为Loc[1,1,1],ai11的地址为Loc[i,1,1]=Loc[1,1,1]+(i-1)*m*n ,那么求任意元素aijk的地址计算公式为:Loc[i,j,k]=Loc[1,1,1]+(i-1)*m*n+(j-1)*n+(k-1)
其中1≤i≤r,1≤j≤m,1≤k≤n。
如果将三维数组推广到一般情况,即:用j1,j2,j3代替数组下标i,j,k;并且j1,j2,j3的下限为c1,c2,c3,上限分别为d1,d2,d3,每个元素占一个存储单元。则三维数组中任意元素a(j1,j2,j3)的地址为:
Loc[j1,j2,j3]=Loc[c1,c2,c3]+1*(d2-c2+1)*(d3-c3+1)*(j1-c1)+1*(d3-c3+1)*(j2-c2)+1*(j3-c3)
其中l为每个元素所占存储单元数。
三、特殊矩阵的压缩存储
特殊矩阵压缩存储的压缩原则是:对有规律的元素和值相同的元素只分配一个存储单元,对于零元素不分配空间。
1、三角矩阵
三角矩阵大体分为:下三角矩阵、上三角矩阵和对称矩阵。对于一个n阶矩阵A来说:
若当i<j时,有aij=0,则称此矩阵为下三角矩阵;
若当 i>j时,有aij=0,则此矩阵称为上三角矩阵;
若矩阵中的所有元素均满足aij=aji,则称此矩阵为对称矩阵。
下三角矩阵:
对于下三角矩阵,按“行序为主序”进行存储,得到的序列为:a11,a21,a22,a31,a32,a33…an1,an2…ann。由于下三角矩阵的元素个数为n(n+1)/2,所以可压缩存储到一个大小为n(n+1)/2的一维数组中。下三角矩阵中元素aij(i>j),在一维数组A中的位置为:
LOC[ i ,j]= LOC[1,1]+ i (i -1)/2+ j-1
同样,对于上三角矩阵,也可以将其压缩存储到一个大小为n(n+1)/2的一维数组C中。其中元素aij(i<j)在数组C中的存储位置为:
Loc[i,j]= Loc[1,1]+j(j -1)/2+ i-1
对于对称矩阵,因其元素满足aij=aji,我们可以为每一对相等的元素分配一个存储空间,即只存下三角(或上三角)矩阵,从而将n²个元素压缩到n(n+1)/2个空间中。
2、带状矩阵
带状矩阵:在矩阵A中,所有的非零元素都集中在以主对角线为中心的带状区域中。最常见的是三对角带状矩阵。
特点:

三对角带状矩阵的压缩存储,以行序为主序进行存储,并且只存储非零元素。其方法为:
1). 确定存储该矩阵所需的一维向量空间的大小
从三对角带状矩阵中可看出:除第一行和最后一行只有两个元素外,其余各行均有3个非零元素。由此可得到一维向量所需的空间大小为:3n-2。
2). 确定非零元素在一维数组空间中的位置
LOC[i , j] = LOC[1,1]+3×(i-1)-1+j-i+1=LOC[1,1]+2(i-1)+j-1
3、稀疏矩阵
稀疏矩阵:指矩阵中大多数元素为零的矩阵。一般地,当非零元素个数只占矩阵元素总数的25%—30%,或低于这个百分数时,我们称这样的矩阵为稀疏矩阵。
(1)稀疏矩阵的三元组表表示法
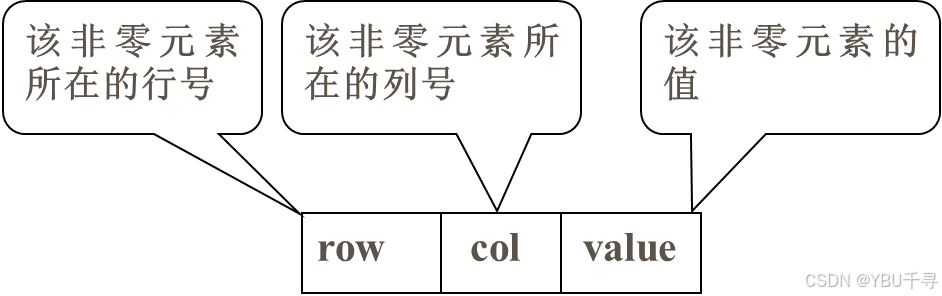
对于稀疏矩阵的压缩存储要求在存储非零元素的同时,还必须存储该非零元素在矩阵中所处的行号和列号。我们将这种存储方法叫做稀疏矩阵的三元组表示法。
每个非零元素在一维数组中的表示形式如图所示:
三元组表的类型说明:
#define MAXSIZE 1000 /*非零元素的个数最多为1000*/
typedef struct
{int row, col; /*该非零元素的行下标和列下标*/
ElementType e; /*该非零元素的值*/
}Triple;
typedef struct
{Triple data[MAXSIZE+1]; /* 非零元素的三元组表 。data[0]未用*/
int m, n, len; /*矩阵的行数、列数和非零元素的个数*/
}TSMatrix;
a)用三元组表实现稀疏矩阵的转置运算
矩阵转置:指变换元素的位置,把位于(row,col)位置上的元素换到(col ,row)位置上,也就是说,把元素的行列互换。
采用矩阵的正常存储方式时,实现矩阵转置的经典算法如下:
Void TransMatrix(ElementType source[n][m], ElementType dest[m][n])
{/*Source和dest分别为被转置的矩阵和转置后的矩阵(用二维数组表示)*/
int i, j;
for(i=0;i<m;i++)
for (j=0;j< n;j++)
dest[i][j]=source[j] [i] ;
}实现转置的简单方法:
①矩阵source的三元组表A的行、列互换就可以得到B中的元素,如图 :
②为了保证转置后的矩阵的三元组表B也是以“行序为主序”进行存放,则需要对行、列互换后的三元组B,按B的行下标(即A的列下标)大小重新排序。
两种处理转置算法如下:
算法一:
void TransposeTSMatrix(TSMatrix A, TSMatrix * B)
{ /*把矩阵A转置到B所指向的矩阵中去。矩阵用三元组表表示*/
int i , j, k ;
B->m= A.n ; B->n= A.m ; B->len= A.len ;
if(B->len>0)
{ j=1;
for(k=1; k<=A.n; k++)
for(i=1; i<=A.len; i++)
if(A.data[i].col==k)
{ B->data[j].row=A.data[i].col
B->data[j].col=A.data[i].row; B->data[j].e=A.data[i].e; j++;
}
}
}算法二:
FastTransposeTSMatrix (TSMatrix A, TSMatrix * B)
{ /*基于矩阵的三元组表示,采用快速转置法,将矩阵A转置为B所指的矩阵*/
int col , t , p,q; int num[MAXSIZE], position[MAXSIZE] ;
B->len= A.len ; B->n= A.m ; B->m= A.n ;
if(B->len)
{for(col=1;col<=A.n;col++) num[col]=0;
for(t=1;t<=A.len;t++) num[A.data[t].col]++; /*计算每一列的非零元素的个数*/
position[1]=1;
for(col=2;col<A.n;col++) /*求col列中第一个非零元素在B.data[ ]中的正确位置*/
position[col]=position[col-1]+num[col-1];
for(p=1;p<A.len.p++)
{ col=A.data[p].col; q=position[col]; B->data[q].row=A.data[p].col;
B->data[q]..col=A.data[p].row; B->data[q].e=A.data[p].e
position[col]++;
}
}
}
用三元组表实现稀疏矩阵的乘法运算
设矩阵M是m1×n1矩阵,N是m2×n2矩阵;若可以相乘,则必须满足矩阵M的列数n1与矩阵N的行数m2相等,才能得到结果矩阵Q=M×N(一个m1×n2的矩阵)。
数学中矩阵Q中的元素的计算方法如下:
其中:1≤i≤m1,1≤j≤n2
根据数学上矩阵相乘的原理,我们可以得到矩阵相乘的经典算法:
for(i=1;i<=m1;i++)
for(j=1;j<=n2;j++)
{ Q[i][j]=0;
for(k=1;k<=n1;k++)
Q[i][j]= Q[i][j]+M[i][k]*N[k][j];
}
经典算法中,不论M[i][k],N[k][j]是否为零,都要进行一次乘法运算,而实际上,这是没有不必要的。采用三元组表的方法来实现时,因为三元组只对矩阵的非零元素做存储,所以可以采用固定三元组a中元素(i,k,Mik)(1≤i≤m1,1≤k≤n1),在三元组b中找所有行号为k的的对应元素(k,j,Nkj)(1≤k≤m2,1≤j≤n2)进行相乘、累加从而得到Q[i][j]。即:以三元组a中的元素为基准,依次求出其与三元组b的有效乘积。
相乘基本操作:对于三元组a中每个元素a.data[p](p=1,2,3,…a.len),找出三元组b中所有满足条件a.data[p].col=b.data[q].row的元素b.data[q],求得a.data[p].e与b.data[q].e的乘积,而这个乘积只是Q[i,j]的一部分,应对每个元素设一个累计和变量,其初值为0。扫描完三元组a,求得相应元素的乘积并累加到适当的累计和的变量上。
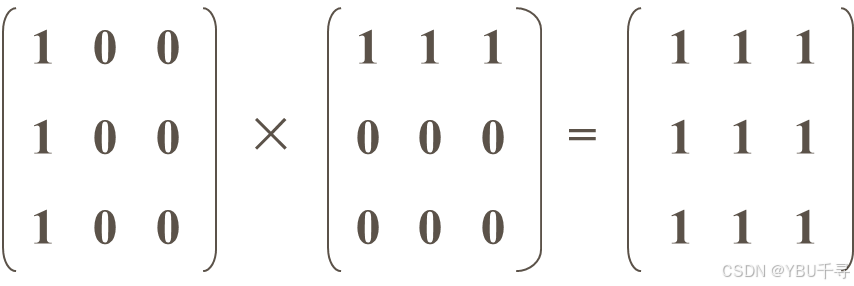
注意:两个稀疏矩阵相乘的结果不一定是稀疏矩阵。反之,相乘的每个分量M[i,k]×N[k,j]不为零,但累加的结果Q[i,j]可能是零。 例如:
为方便实现,将三元组表的类型说明修改如下:
#define MAXSIZE 1000 /*非零元素的个数最多为1000*/
#define MAXROW 1000 /*矩阵最大行数为1000*/
typedef struct
{int row, col; /*该非零元素的行下标和列下标*/
ElementType e; /*该非零元素的值*/
}Triple;
typedef struct
{ Triple data[MAXSIZE+1]; /* 非零元素的三元组表,data[0]未用*/
int first[MAXROW+1];
/*三元组表中各行第一个非零元素所在的位置。*/
int m, n, len; /*矩阵的行数、列数和非零元素的个数*/
}TriSparMatrix;
具体算法如下:
int MulSMatrix(TriSparMatrix M, TriSparMatrix N, TriSparMatrix *Q)
{/*采用改进的三元组表表示法,求矩阵乘积Q=M×N*/
int arow , brow , p; int ctemp[MAXSIZE];
if(M.n!=N.m) return FALSE; /*返回FALSE表示求矩阵乘积失败*/
Q->m=M.m; Q->n=N.n; Q->len=0;
if(M.len*N.len!=0)
{for(arow=1; arow<=M.m; arow++) /*逐行处理M*/
{for(p=1;p<=M.n;p++)
ctemp[p]=0 ; /* 当前行各元素的累加器清零*/
Q->first[arow]=Q->len+1;
for(p=M.first[arow];p<M.first[arow+1];p++) /*p指向M当前行中每一个非零元素*/
{brow=M.data[p].col; /* M中的列号应与N中的行号相等*/
if(brow<N.n) t=N.first[brow+1]; else t=N.len+1;
for(q=N.first[brow];q<t;q++)
{ccol=N.data[q].col; /*乘积元素在Q中列号*/
ctemp[ccol]+=M.data[p].e*N.data[q].e; } /* for q */
} /*求得Q中第crow行的非零元*/
for(ccol=1;ccol<Q->n;col++) /*压缩存储该非零元*/
if(ctemp[ccol])
{if(++Q->len>MAXSIZE) return 0;
Q->data[Q->len]={arow, ccol, ctemp[ccol]};
}/* if */ }/* for arow */
}/*if*/ return(TRUE); /*返回TRUE表示求矩阵乘积成功*/
}
(2)稀疏矩阵的链式存储结构:十字链表
优点:它能够灵活地插入因运算而产生的新的非零元素,删除因运算而产生的新的零元素,实现矩阵的各种运算。
在十字链表中,矩阵的每一个非零元素用一个结点表示,该结点除了(row,col,value)以外,还要有两个域:
right: 用于链接同一行中的下一个非零元素;
down:用以链接同一列中的下一个非零元素。
十字链表中结点的结构示意图:
| row | col | value | |
| down | right | ||
十字链表的结构类型说明如下:
typedef struct OLNode
{ int row, col; /*非零元素的行和列下标*/
ElementType value;
struct OLNode * right,*down; /*非零元素所在行表列表的后继链域*/
}OLNode; *OLink;
typedef struct
{ OLink * row_head, *col_head; /*行、列链表的头指针向量*/
int m, n, len; /*稀疏矩阵的行数、列数、非零元素的个数*/
}CrossList;
建立稀疏矩阵的十字链表算法:
CreateCrossList (CrossList * M)
{/*采用十字链表存储结构,创建稀疏矩阵M*/
if(M!=NULL) free(M);
scanf(&m,&n,&t); /*输入M的行数,列数和非零元素的个数*/
M->m=m;M->n=n;M->len=t;
If(!(M->row_head=(Olink*)malloc((m+1)sizeof(OLink)))) exit(OVERFLOW);
If(!(M->col_head=(OLink * )malloc((n+1)sizeof(OLink)))) exit(OVERFLOW);
M->row_head[ ]=M->col_head[ ]=NULL; /*初始化行、列头指针向量,各行、列链表为空的链表*/
for(scanf(&i,&j,&e);i!=0; scanf(&i,&j,&e))
{if(!(p=(OLNode *) malloc(sizeof(OLNode)))) exit(OVERFLOW);
p->row=i;p->col=j;p->value=e; /*生成结点*/
if(M->row_head[i]==NULL) M->row_head[i]=p;
else{ /*寻找行表中的插入位置*/
for(q=M->row_head[i]; q->right&&q->right->col<j; q=q->right)
p->right=q->right; q->right=p; /*完成插入*/
}
if(M->col_head[j]==NULL) M->col_head[j]=p;
else{ /*寻找列表中的插入位置*/
for(q=M->col_head[j]; q->down&&q->down->row<i; q=q->down)
p->down=q->down; q->down=p; /*完成插入*/
}
}
} 四、广义表
广义表也是线性表的一种推广。广义表也是n个数据元素(d1,d2,d3,…,dn)的有限序列,但不同的是,广义表中的di既可以是单个元素,还可以是一个广义表,通常记作:GL=(d1,d2,d3,…,dn)。GL是广义表的名字,通常用大写字母表示。n是广义表的长度。若 di是一个广义表,则称di是广义表GL的子表。 在GL中, d1是GL的表头,其余部分组成的表(d2,d3,…,dn)称为GL的表尾。由此可见,广义表的定义是递归定义的。
例如:
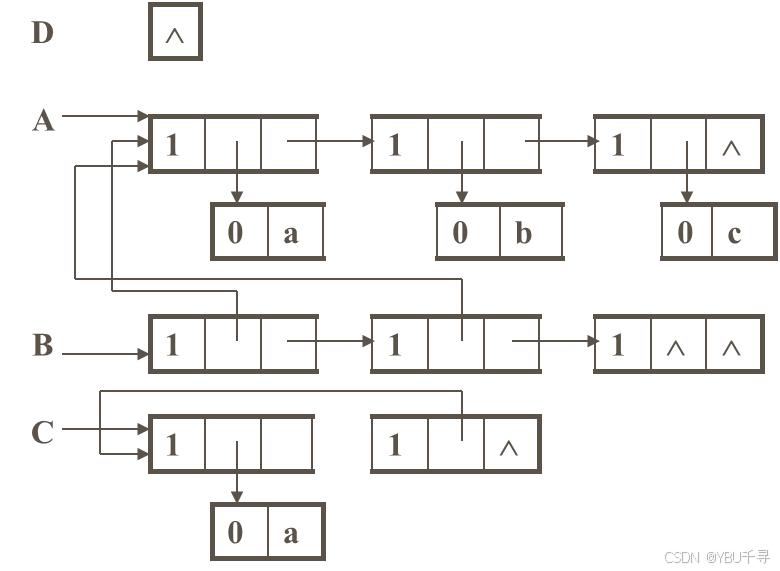
D=() 空表;其长度为零。
A=(a,(b,c))表长度为2的广义表,其中第一个元素是单个数据a,第二个元素是一个子表(b,c)。
B=(A,A,D)长度为3的广义表,其前两个元素为表A,第三个元素为空表D。
C=(a,C) 长度为2递归定义的广义表,C相当于无穷表C=(a,(a,(a,(…))))。
head(A)=a 表A的表头是a。
tail(A)=((b,c)) 表A的表尾是((b,c)) ,广义表的表尾一定是一个表。
从上面的例子可以看出:
(1)广义表的元素可以是子表,而子表还可以是子表…,由此,广义表是一个多层的结构。
(2)广义表可以被其他广义表共享。如:广义表B就共享表A。在表B中不必列出表A的内容,只要通过子表的名称就可以引用该表。
(3)广义表具有递归性,如广义表C。
广义表中有两类结点,一类是单个元素结点,一类是子表结点。任何一个非空的广义表都可以将其分解成表头和表尾两部分,反之,一对确定的表头和表尾可以唯一地确定一个广义表。由此,一个表结点可由三个域构成:标志域,指向表头的指针域,指向表尾的指针域。而元素结点只需要两个域:标志域和值域。
广义表A、B、C、D的存储结构图如下所示:
广义表的头尾链表存储结构:
typedef enum {ATOM, LIST} ElemTag;
/* ATOM=0,表示原子;LIST=1,表示子表*/
typedef struct GLNode
{ ElemTag tag; /*标志位tag用来区别原子结点和表结点*/
union
{ AtomType atom; /*原子结点的值域atom*/
struct { struct GLNode * hp, *tp;} htp;
/*表结点的指针域htp, 包括表头指针域hp和表尾指针域tp*/
} atom_htp;
/* atom_htp 是原子结点的值域atom和表结点的指针域htp的联合体域*/
} *GList;
另外,还有一种广义表存储结构,在这种结构中,无论是单元素结点还是子表结点均由三个域构成。 其结点结构图为:
广义表的第二种存储结构图如下所示:
广义表的扩展线性链表存储结构 :
typedef enum {ATOM,LIST} ElemTag;
/* ATOM=0,表示原子;LIST=1,表示子表*/
typedef struct GLNode
{ ElemTag tag;
union
{ AtomType atom;
struct GLNode * hp;
} atom_hp;
struct GLNode * tp;
} *GList;
广义表的操作实现举例
下面以广义表的头尾链表存储结构为例,介绍广义表的几个基本操作。
1、求广义表的表头和表尾
GList Head(GList L)
{
if(L==NULL) return(NULL); /* 空表无表头 */
if(L->tag==ATOM) exit(0); /* 原子不是表 */
else return(L->atom_htp.htp.hp);
}
GList Tail(GList L)
{
if(L==NULL) return(NULL); /* 空表无表尾 */
if(L->tag==ATOM) exit(0); /* 原子不是表*/
else return(L->atom_htp.htp.tp);
}
2、求广义表的长度
int Length(GList L)
{ int n=0;
GLNode *s;
if(L==NULL) return(0); /* 空表长度为0 */
if(L->tag==ATOM) exit(0); /* 原子不是表 */
s=L;
while(s!=NULL) /* 统计最上层表的长度 */
{ k++;
s=s->atom_htp.htp.tp;
}
return(k);
}3、求广义表的深度
int Depth(GList L)
{ int d, max;
GLNode *s;
if(L==NULL) return(1); /* 空表深度为1 */
if(L->tag==ATOM) return(0); /* 原子深度为0 */
s=L;
while(s!=NULL) /* 求每个子表的深度的最大值 */
{ d=Depth(s->atom_htp.htp.hp);
if(d>max) max=d;
s=s->atom_htp.htp.tp;
}
return(max+1); /* 表的深度等于最深子表的深度加1 */
}
4、统计广义表中原子数目
int CountAtom(GList L)
{ int n1, n2;
if(L==NULL) return(0); /* 空表中没有原子 */
if(L->tag==ATOM) return(1); /* L指向单个原子 */
n1=CountAtom(L->atom_htp.htp.hp); /* 求表头中的原子数 */
n2=CountAtom(L->atom_htp.htp.tp); /* 求表尾中的原子数 */
return(n1+n2);
}
5、复制广义表
int CopyGList(GList S, GList *T)
{ if(S==NULL) { *T=NULL; return(OK); } /* 复制空表 */
*T=(GLNode *)malloc(sizeof(GLNode));
if(*T==NULL) return(ERROR);
(*T)->tag=S->tag;
if(S->tag==ATOM) (*T)->atom=S->atom; /* 复制单个原子 */
else
{ CopyGList(S->atom_htp.htp.hp, &((*T)->atom_htp.htp.hp));
/* 复制表头 */
CopyGList(S->atom_htp.htp.tp, &((*T)->atom_htp.htp.tp));
/* 复制表尾 */
}
return(OK);
}
以下给出几个经典例题
例1
已知数组M[1..10, -1..6, 0..3],求:
(1)数组的元素总数;
(2)若数组以下标顺序为主序存储,起始地址为1000,且每个数据元素占用3个存储单元,试分别计算M[2, 4, 2], M[5, -1, 3]的地址。
解:
(1)数组的元素总数为:(10-1+1)×(6-(-1)+1)×(3-0+1)=320
(2)地址计算公式为:
Loc[i, j, k] = Loc[c1,c2,c3] + ( (d2-c2+1)×(d3-c3+1)×(i-c1) +(d3-c3+1)×(j-c2) +(k-c3) )×size
在此c1=1,d1=10,c2=-1,d2=6,c3=0,d3=3,所以:
Loc[2, 4, 2] = 1000 + ( (6-(-1)+1)×(3-0+1)×(2-1) +(3-0+1)×(4-(-1)) +(2-0) )×3=1162
Loc[5, -1, 3] = 1000 + ( (6-(-1)+1)×(3-0+1)×(5-1) +(3-0+1)×(-1-(-1)) +(3-0) )×size=1393
例2 已知广义表L=((x, y, z), a, (u, t, w)),从L表中取出原子u的运算是:
A) head(tail(tail(L))) B) tail(head(head(tail(L))))
C) head(tail(head(tail(L)))) D) head(head(tail(tail(L))))
解:取出原子u的过程如下:
1)用tail运算去掉表头 (x, y, z),即:tail(L) = (a, (u, t, w))
2)再用tail运算去掉表头a,即:tail(tail(L)) = ((u, t, w))
3)用head运算取出表头 (u, t, w),即:
head(tail(tail(L))) = (u, t, w)
4)再用head运算取出表头u,即:head(head(tail(tail(L)))) = u
本篇内容不太详细,敬请大家指点!!!