本篇适用于ZZU的编译原理课程实验二——自动机实验:NFA转DFA并最小化,包含了实验代码和实验报告的内容,读者可根据需要参考完成自己的程序设计。
如果是ZZU的学弟学妹看到这篇,那么恭喜你,你来对地方啦!
如果需要相关文档资料的话,我也已经上传,免费下载:「编译原理实验二代码+实验报告(ZZU)」
不要忘了点赞👍和收藏💌支持一下哦!
源代码
先给出实验的源代码
#include <iostream>
#include <fstream>
#include <vector>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <sstream>
using namespace std;
// NFA类定义
struct NFA {
set<int> states; // 状态集合
set<int> alphabet; // 字母表
map<pair<int,int>, set<int>> transitions; // 转移函数 F(fromState, symbol)={toStates}
int start_state{}; // 初始状态
set<int> accept_states; // 接受状态集合
};
// DFA类定义
struct DFA {
set<int> states; // 状态集合
set<int> alphabet; // 字母表
map<pair<int,int>, int> transitions; // 转移函数
int start_state{}; // 初始状态
set<int> accept_states; // 接受状态集合
};
// 从文件读取NFA
NFA readNFAFromFile(const string& filename) {
NFA nfa;
ifstream file(filename);
string line;
// 读取状态集合
getline(file, line);
istringstream iss(line); // 将一行数据转换成一个输入流,随后可以像处理文件或标准输入一样从`iss`中提取数据
int state;
while (iss >> state) { // 从转换好后的每一行输入中,逐个读取整数作为状态`state`
nfa.states.insert(state);
}
// 读取字母表
getline(file, line);
iss.clear(); // 重置流状态
iss.str(line); // 读取新的一行作为流
int symbol; // 输入的标志字母
while (iss >> symbol) {
nfa.alphabet.insert(symbol);
}
// 读取转移规则数量
int trans_count;
file >> trans_count;
// 读取转移规则
for (int i = 0; i < trans_count; i++) {
int from_state, now_symbol; // 当前状态,转换字母
file >> from_state >> now_symbol; // 从文件中读取
set<int> to_states_set; // 目标状态集合
int to_state; // 目标状态
// 读取目标状态,添加到到目标状态集合
while (file.get() != '\n' && file >> to_state) {
to_states_set.insert(to_state);
}
nfa.transitions[{from_state, now_symbol}] = to_states_set; // 转移函数 F(fromState, symbol)={toState}
}
// 读取初始状态和接受状态
file >> nfa.start_state;
int accept_state;
file >> accept_state;
nfa.accept_states.insert(accept_state);
return nfa;
}
// 获取ε-闭包集合
set<int> getEpsilonClosure(const NFA& nfa, const set<int>& states) {
set<int> closure = states;
// 队列进行存储状态集合states
queue<int> q;
for (int state : states) {
q.push(state);
}
while (!q.empty()) {
// 从前往后弹出状态
int current = q.front();
q.pop();
// 对每个状态进行判断闭包
auto it = nfa.transitions.find({current, -1}); // 查找转换函数中的当前状态的所有ε边
if (it != nfa.transitions.end()) {
for (int next : it->second) { // it中的元素为键值对类型pair,second就是获取键值对的后一个值
if (closure.find(next) == closure.end()) { // 未被记录进闭包集合
closure.insert(next);
q.push(next);
}
}
}
}
return closure;
}
// 合并两个NFA
NFA mergeNFAs(const NFA& nfa1, const NFA& nfa2) {
NFA merged;
// 找到最大状态编号
int max_state = 0;
for (int state : nfa1.states) max_state = max(max_state, state);
for (int state : nfa2.states) max_state = max(max_state, state);
// 新的起始状态
int new_start = max_state + 1;
merged.start_state = new_start;
// 合并状态集
merged.states = nfa1.states;
merged.states.insert(nfa2.states.begin(), nfa2.states.end());
merged.states.insert(new_start);
// 合并字母表
merged.alphabet = nfa1.alphabet;
merged.alphabet.insert(nfa2.alphabet.begin(), nfa2.alphabet.end());
// 合并转移函数
merged.transitions = nfa1.transitions;
for (const auto& trans : nfa2.transitions) {
merged.transitions[trans.first] = trans.second;
}
// 添加从新起始状态到原始NFA起始状态的ε转移
merged.transitions[{new_start, -1}].insert(nfa1.start_state);
merged.transitions[{new_start, -1}].insert(nfa2.start_state);
// 合并接受状态
merged.accept_states = nfa1.accept_states;
merged.accept_states.insert(nfa2.accept_states.begin(), nfa2.accept_states.end());
return merged;
}
// NFA转换为DFA
DFA convertNFAtoDFA(const NFA& nfa) {
DFA dfa;
map<set<int>, int> dfa_states; // nfa状态集 --> dfa的一个状态
queue<set<int>> unprocessed_states;
// 初始化DFA
dfa.alphabet = nfa.alphabet;
// 求DFA的起始状态
set<int> initial_state = getEpsilonClosure(nfa, {nfa.start_state});
dfa_states[initial_state] = 0;
dfa.start_state = 0;
unprocessed_states.push(initial_state); // 将dfa起始状态集加入已处理状态队列
// 使用子集构造法构建DFA
while (!unprocessed_states.empty()) {
set<int> current_state = unprocessed_states.front();
unprocessed_states.pop();
int dfa_state = dfa_states[current_state];
// 检查是否为接受状态
for (int state : current_state) {
if (nfa.accept_states.find(state) != nfa.accept_states.end()) {
dfa.accept_states.insert(dfa_state);
break;
}
}
// 对每个输入符号构造转移
for (int symbol : nfa.alphabet) {
set<int> next_state;
// 将当前状态的多条转移合并
for (int state : current_state) {
auto it = nfa.transitions.find({state, symbol});
if (it != nfa.transitions.end()) {
next_state.insert(it->second.begin(), it->second.end()); // 多条转移的终点合并加入到当前状态集合的目标状态集合
// 实现多条转移合并为一条集合与集合之间的转移
}
}
// 计算ε-闭包
next_state = getEpsilonClosure(nfa, next_state);
if (!next_state.empty()) {
// 判断是否是新状态
if (dfa_states.find(next_state) == dfa_states.end()) {
int new_state = dfa_states.size(); // 为新状态进行编号
dfa_states[next_state] = new_state;
unprocessed_states.push(next_state);
}
dfa.transitions[{dfa_state, symbol}] = dfa_states[next_state];
}
}
}
// 设置DFA状态集
for (const auto& state : dfa_states) {
dfa.states.insert(state.second);
}
return dfa;
}
// DFA最小化
DFA minimizeDFA(const DFA& dfa) {
// 初始划分:接受状态和非接受状态
vector<set<int>> partitions(2);
map<int, int> partition_map;
for (int state : dfa.states) {
if (dfa.accept_states.find(state) != dfa.accept_states.end()) {
partitions[0].insert(state);
partition_map[state] = 0;
} else {
partitions[1].insert(state);
partition_map[state] = 1;
}
}
bool changed; // 标记划分是否改变
do {
changed = false;
vector<set<int>> new_partitions; // 新的划分
for (const auto& partition : partitions) {
if (partition.size() <= 1) {
new_partitions.push_back(partition);
continue;
}
map<vector<int>, set<int>> subdivision; // 子划分
for (int state : partition) {
vector<int> parts; // 划分号
for (int symbol : dfa.alphabet) {
auto it = dfa.transitions.find({state, symbol});
if (it != dfa.transitions.end()) {
parts.push_back(partition_map[it->second]);
} else {
parts.push_back(-1);
}
}
subdivision[parts].insert(state);
}
for (const auto& sub : subdivision) {
new_partitions.push_back(sub.second);
if (sub.second.size() != partition.size()) {
changed = true;
}
}
}
// 发生了改变
if (changed) {
partitions = new_partitions;
partition_map.clear();
for (size_t i = 0; i < partitions.size(); i++) {
for (int state : partitions[i]) {
partition_map[state] = i;
}
}
}
} while (changed);
// 构建最小化DFA
DFA min_dfa;
min_dfa.alphabet = dfa.alphabet;
// 映射旧状态到新状态
map<int, int> state_map;
int new_state_id = 0;
for (const auto& partition : partitions) {
for (int state : partition) {
if (state_map.find(state) == state_map.end()) {
state_map[state] = new_state_id;
min_dfa.states.insert(new_state_id);
if (state == dfa.start_state) {
min_dfa.start_state = new_state_id;
}
if (dfa.accept_states.find(state) != dfa.accept_states.end()) {
min_dfa.accept_states.insert(new_state_id);
}
new_state_id++;
}
}
}
// 构建新的转移函数
for (const auto& trans : dfa.transitions) {
int from_state = state_map[trans.first.first];
int symbol = trans.first.second;
int to_state = state_map[trans.second];
min_dfa.transitions[{from_state, symbol}] = to_state;
}
return min_dfa;
}
// 打印DFA
void printDFA(const DFA& dfa) {
cout << "DFA\n";
cout << " 状态集:{";
for (auto it = dfa.states.begin(); it != dfa.states.end(); ++it) {
if (it != dfa.states.begin()) cout << ",";
cout << *it;
}
cout << "}\n";
cout << " 符号表:{";
for (auto it = dfa.alphabet.begin(); it != dfa.alphabet.end(); ++it) {
if (it != dfa.alphabet.begin()) cout << ",";
cout << *it;
}
cout << "}\n";
cout << " 状态转换:\n";
for (const auto& trans : dfa.transitions) {
cout << " (" << trans.first.first << ","
<< trans.first.second << ")->"
<< trans.second << "\n";
}
cout << " 开始状态:" << dfa.start_state << "\n";
cout << " 结束状态集:{";
for (auto it = dfa.accept_states.begin(); it != dfa.accept_states.end(); ++it) {
if (it != dfa.accept_states.begin()) cout << ",";
cout << *it;
}
cout << "}\n";
}
int main() {
// 从文件读取NFA
NFA nfa1 = readNFAFromFile("experiment02_input1.txt");
NFA nfa2 = readNFAFromFile("experiment02_input2.txt");
// 合并NFA
NFA merged_nfa = mergeNFAs(nfa1, nfa2);
// 转换为DFA
DFA dfa = convertNFAtoDFA(merged_nfa);
// 最小化DFA
DFA min_dfa = minimizeDFA(dfa);
// 输出结果
printDFA(min_dfa);
return 0;
}
实验报告
接下来是实验报告的内容,希望能帮助读者理解词法分析程序的设计思路,以及完成实验报告的撰写。
一.实验目的
- 理解和掌握把问题中的实体转换成抽象模型中数据结构的能力,设计确定有穷自动机DFA和非确定有穷自动机NFA描述的对象模型或数据结构,实现DFA和NFA的基本操作(输入和输出);
- 掌握将多个NFA合并的方法;
- 掌握将NFA确定化成DFA的方法;
- 掌握将DFA最小化的方法。
加深对自动机的理解。
二.问题描述
-
需要实现的功能
(1)设计一个函数(方法),实现把两个NFA的合并;
(2)设计一个函数(方法),实现把NFA确定化成一个DFA;
(3)设计一个函数(方法),实现把DFA最小化;
(4)输入多个NFA:NFA描述存储在文本文件中,文件名作为命令行参数输入;
(5)输出合并、最小化以后的DFA到标准输出设备。 -
实现原理
2.1 NFA合并
(1)创建新的开始状态
(2)通过ε-转换连接到原NFA的开始状态
(3)合并状态集、字母表、转移函数和接受状态
2.2 NFA确定化
(1)使用子集构造法
(2)计算ε-闭包
(3)构造新的状态转移函数
2.3 DFA最小化
(1)基于等价类的划分算法
(2)初始划分为接受状态和非接受状态
(3)迭代细化状态划分直至稳定
三.软件设计方法的选择
-
设计方法
采用结构化设计方法,主要是考虑到了:
(1)问题本身具有清晰的数据流向和处理流程
(2)功能模块划分明确
(3)算法实现较为直观 -
各阶段创建的模型
2.1 分析阶段:
(1)系统流程图
(2)数据流图
(3)数据字典
2.2 设计阶段:
(4)模块结构图
(5)数据结构设计
(6)算法流程图 -
开发环境
编程语言: C++11
编译器: g++
开发工具: CLion
依赖库: STL标准模板库
四.分析模型
- 系统流程图
描述:
开始:实验的起始点,系统准备开始执行。
读取NFA1与读取NFA2:从输入文件中读取两个非确定有穷自动机(NFA)的描述信息。
合并NFA:将两个NFA进行合并,创建一个新的NFA,合并后的NFA需要合并状态集、字母表、转移函数等。
转换为DFA:通过子集构造法将NFA转换为确定性有限自动机(DFA)。
最小化DFA:对转换后的DFA进行最小化,减少状态数并简化自动机结构。
输出结果:输出最小化后的DFA描述,显示其状态集、转移函数等信息。
结束:实验完成。

2.数据流图
描述:
NFA描述文件:输入文件,包含NFA的定义,如状态集、转移函数、字母表、起始状态和接受状态等。
读取NFA:读取输入文件中的NFA描述并将其转化为程序内部使用的NFA数据结构。
NFA合并:将多个NFA合并为一个新的NFA,该步骤是通过创建一个新的起始状态并加入适当的ε转移来实现的。
NFA转DFA:通过子集构造法将NFA转换成DFA。此过程涉及计算状态的ε-闭包,并构建转移函数。
DFA最小化:对DFA进行最小化处理,使用等价类划分法将DFA的状态集划分为等价类,合并等价状态,减少状态数。
标准输出:输出最小化后的DFA的各项信息,包括状态集、接受状态、转移函数。
3.数据字典
3.1 NFA结构
NFA = {
states: 状态集合
alphabet: 字母表
transitions: 转移函数
start_state: 初始状态
accept_states: 接受状态集合
}
描述:
states:NFA中的状态集合。
alphabet:NFA的输入字母表,包含所有可能的输入符号。
transitions:转移函数,定义了从一个状态出发,在特定输入下转移到哪些状态(包括ε转移)。
start_state:NFA的起始状态,是计算开始的状态。
accept_states:NFA的接受状态集合,表示能接受输入字符串的状态。
3.2 DFA结构
DFA = {
states: 状态集合
alphabet: 字母表
transitions: 转移函数
start_state: 初始状态
accept_states: 接受状态集合
}
描述:
states:DFA中的状态集合。
alphabet:DFA的输入字母表,通常与NFA的字母表相同。
transitions:转移函数,定义了在每个状态下,输入符号如何转移到另一个状态。
start_state:DFA的起始状态。
accept_states:DFA的接受状态集合,与NFA的接受状态集合可能不同。
五.设计模型
- 模块结构图
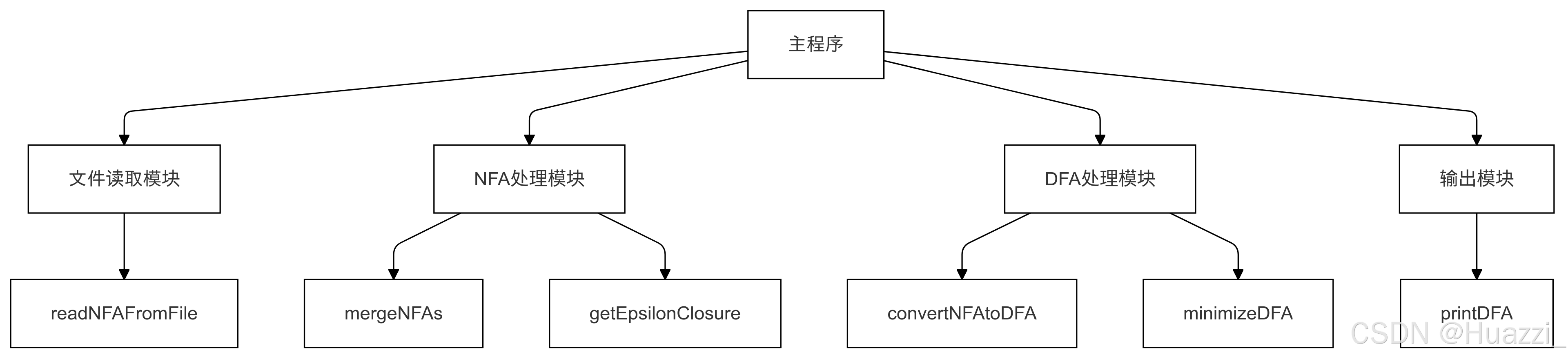
描述:
主程序:程序的核心模块,负责协调其他模块的工作。
文件读取模块:负责从文件中读取NFA的描述,并将其转化为NFA结构。
readNFAFromFile:实现从文件中读取NFA信息,并构造NFA数据结构。
NFA处理模块:负责处理NFA的操作。
mergeNFAs:合并两个NFA,生成一个新的NFA。
getEpsilonClosure:计算NFA状态的ε-闭包。
DFA处理模块:负责将NFA转换为DFA,并对DFA进行最小化。
convertNFAtoDFA:将NFA转换为DFA,使用子集构造法。
minimizeDFA:对DFA进行最小化,减少冗余状态。
输出模块:负责输出最小化后的DFA描述。
printDFA:输出DFA的状态集、接受状态、转移函数等信息。
- 主要数据结构
// NFA结构体
struct NFA {
set<int> states;
set<int> alphabet;
map<pair<int,int>, set<int>> transitions;
int start_state;
set<int> accept_states;
};
// DFA结构体
struct DFA {
set<int> states;
set<int> alphabet;
map<pair<int,int>, int> transitions;
int start_state;
set<int> accept_states;
};
描述:
NFA结构体:定义了NFA的数据结构,其中包括状态集、字母表、转移函数、起始状态和接受状态集。
DFA结构体:定义了DFA的数据结构,类似于NFA,但其转移函数是确定性的,即每个状态对于每个输入符号只有一个确定的转移。
- 主要函数接口
(1)readNFAFromFile:从文件中读取NFA描述,并返回构建好的NFA结构。
(2)getEpsilonClosure:计算给定状态集的ε-闭包,返回一个新的状态集。
(3)mergeNFAs:合并两个NFA,返回合并后的NFA。
(4)convertNFAtoDFA:将给定的NFA转换为DFA。
(5)minimizeDFA:对给定的DFA进行最小化处理,返回最小化后的DFA。
(6)printDFA:输出最小化后的DFA的状态集、转移函数、接受状态等。
六.主要算法描述
- NFA合并算法
NFA算法描述:
寻找最大状态编号:在合并NFA时,首先需要确定新的NFA中的状态编号,应避免与原有NFA中的状态编号冲突。
创建新起始状态:为合并后的NFA创建一个新的起始状态。
合并状态集、字母表、转移函数、接受状态:将两个NFA的状态、字母表、转移函数和接受状态集合并成一个新的NFA。
添加ε转移:通过添加适当的ε转移连接原NFA的起始状态。

- NFA转化DFA算法
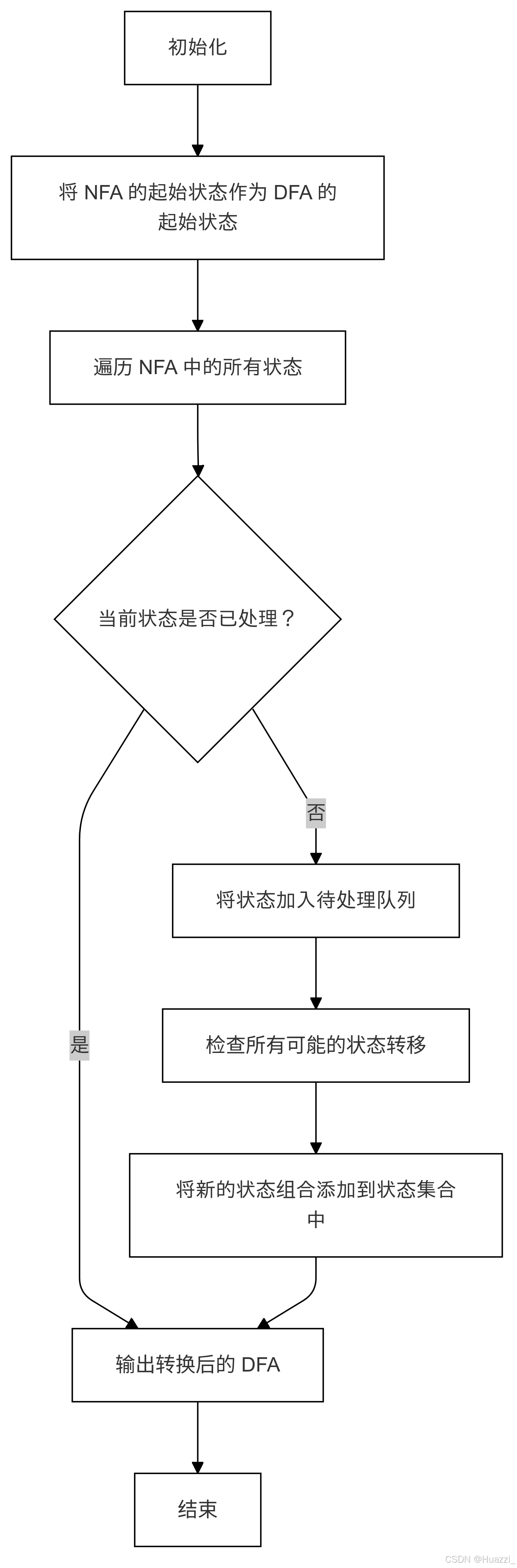
NFA转化DFA算法描述:
计算初始状态ε-闭包:使用ε-闭包计算NFA初始状态的所有可达状态。
初始化DFA:创建一个新的DFA,并将NFA的ε-闭包作为DFA的初始状态。
判断未处理状态队列空:DFA构造过程中需要遍历所有状态,直到没有状态可处理为止。
处理所有输入符号:对于当前状态,遍历所有输入符号,计算对应的下一状态。
更新DFA转移函数:将状态和符号的转移结果添加到DFA的转移函数中。
- DFA最小化算法
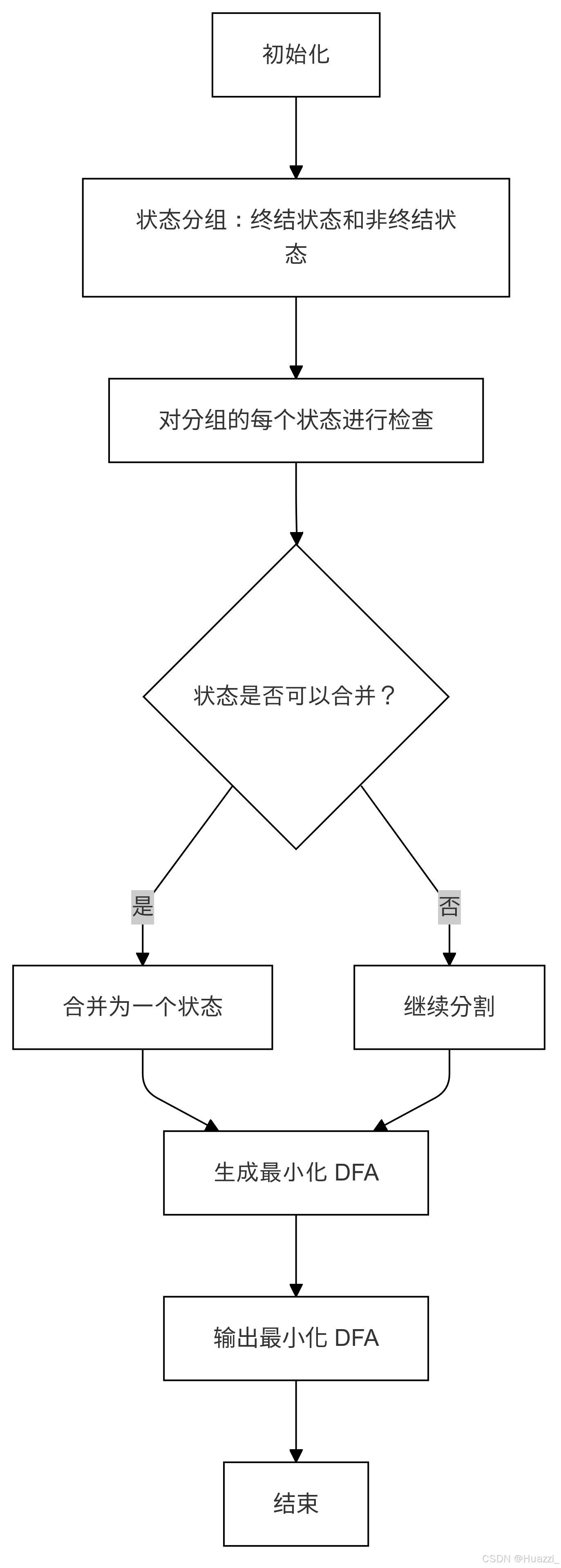
DFA最小化算法描述:
初始划分:最初将状态划分为接受状态和非接受状态。
需要继续划分:检查当前划分是否需要进一步细化。若有相同的转移模式的状态,则需要进一步划分。
对每个划分进行细化:将状态按照它们的转移特征进行细化。
更新划分映射:更新状态划分的映射关系,确保最小化后的状态集满足等价类划分的要求。
-
测试数据格式
输入多个NFA:NFA描述存储在文本文件中,文件名作为命令行参数输入 -
测试数据与测试效果
(1)测试数据1
NFA1:
0 1 2 3 4 5 6 7 8 9 10
0 1
10
0 -1 1 7
1 -1 2 4
2 0 3
3 -1 6
4 1 5
5 -1 6
6 -1 1 7
7 0 8
8 1 9
9 1 10
0
10
NFA2:
11 12 13 14 15 16 17 18
0 1
8
11 -1 12 13
12 0 14
13 1 15
14 -1 16
15 -1 16
16 0 17
17 1 18
11
18
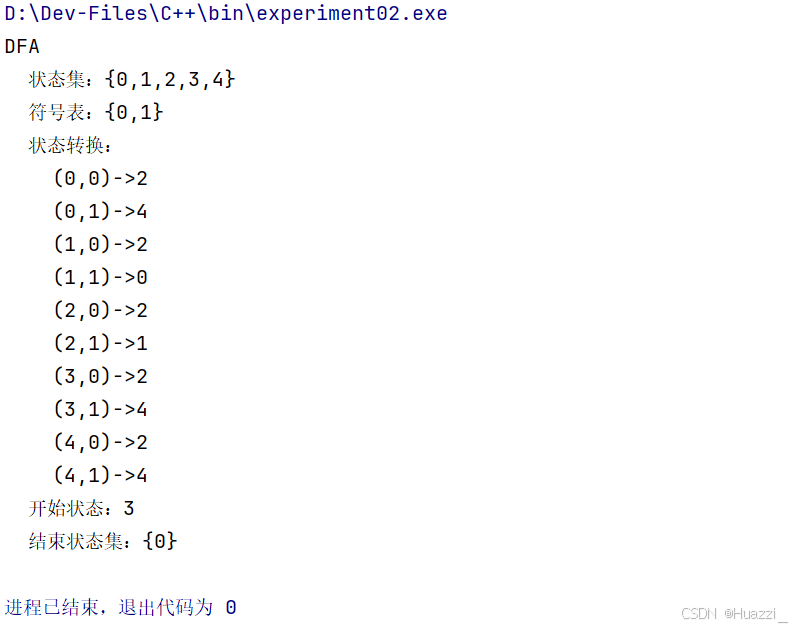
测试效果:
(2)测试数据2
NFA1:
0 1 2 3 4 5 6 7 8 9 10
0 1
6
0 -1 1 5
1 -1 2 4
2 0 3
3 -1 4
4 1 5
5 -1 6
0
6
NFA2:
0 1 2 3 4 5 6 7 8 9 10
0 1
6
0 -1 1 5
1 -1 2 4
2 0 3
3 -1 4
4 1 5
5 -1 6
0
6
测试效果:
根据实验效果,成功输出合并、最小化以后的DFA到标准输出设备。
八.实验总结
-
遇到的问题及解决方法
(1)ε-闭包计算问题:
问题:初始实现时未考虑递归计算ε-闭包
解决:使用队列实现广度优先搜索,确保完整计算闭包
(2)DFA最小化过程中的等价类划分:
问题:划分过程中状态映射更新不及时
解决:每次划分后立即更新状态映射关系
(3)内存管理问题:
问题:大规模NFA转换时内存占用过大
解决:使用STL容器自动管理内存,避免手动内存管理 -
收获与体会
深入理解了自动机理论的实际应用,掌握了复杂算法的工程实现方法,提高了数据结构和算法设计能力,学会了使用STL容器进行高效的数据处理。