引入
在大数据中,常常会有因各种原因而包含缺失值的数据混在数据集中,往往会以NULL,undefined,NaN等出现,忽视它们往往会给模型带来不可预知的后果,所以我们要想办法处理这些数据。
找到缺失值
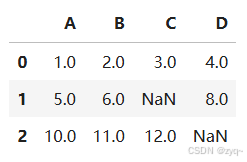
具体寻找方法要根据数据集的结构来设计,我们以最简单的二维表格举例:
import pandas as pd
from io import StringIO
import sys
csv_data = \
'''A,B,C,D
1.0,2.0,3.0,4.0
5.0,6.0,,8.0
10.0,11.0,12.0,'''
# If you are using Python 2.7, you need
# to convert the string to unicode:
if (sys.version_info < (3, 0)):
csv_data = unicode(csv_data)
df = pd.read_csv(StringIO(csv_data))
>>df
对于ski-learn,目前对于numpy和DataFrame都支持,但由于ski-learn对Numpy数组的处理更成熟,一般推荐用Numpy。
我们可以通过DataFrame.values来获取DataFrame底层Numpy数组的数据,之后再放入ski-learn处理。
from sklearn.impute import SimpleImputer
import numpy as np
imr = SimpleImputer(missing_values=np.nan, strategy='mean')
imr = imr.fit(df.values)
imputed_data = imr.transform(df.values)
imputed_data
利用好Numpy和DataFrame的各种操作,可以很方便地对数据地信息进行统计、筛选、查找等操作。
处理数据
删除有缺失值的样本或特征
顾名思义,遇到缺失值,我们可以把这个样本直接删除,或者把有缺失值的特征删除。这种简单粗暴的方式在缺失值发生频率小时可以使用。
删除数据行:
df.dropna(axis=0)
删除特征列:
df.dropna(axis=1)
填补缺失值
往往删除样本或特征容易丢失有价值的数据,我们可以考虑用更精细的方式向空内补上一个数据,以保留这个样本的其他特征的数据,并尽量减少填补的数据对整个训练过程的影响。
最常见的填补方式是均值填补,即用这个特征列其他正常数据的平均值来替代NaN值。ski-learn提供了方便的函数SimpleImputer来实现整个数据集的填补:
# impute missing values via the column mean
from sklearn.impute import SimpleImputer
import numpy as np
imr = SimpleImputer(missing_values=np.nan, strategy='mean')
imr = imr.fit(df.values)
imputed_data = imr.transform(df.values)
imputed_data
当然,我们也可以用pandas来实现,比如:
df.fillna(df.mean())
除了均值填补,我们还可以选择中位数、众数填充,或基于模型来计算填充,如K近邻等,方法类似,这里不作介绍。
忽略缺失值
我们不事先处理缺失值,而是在训练模型的过程中对含缺失值的数据进行特殊的划分策略,以下是《机器学习》提到的方法:
(1)符号说明:
D
D
D为该节点上的训练集;
D
~
\tilde{D}
D~为
D
D
D中没有缺失值的样本子集;
属性
a
a
a和它的
V
V
V个取值
a
i
(
i
=
1
,
2
,
.
.
.
,
V
)
a^{i}(i=1,2,...,V)
ai(i=1,2,...,V);
D
~
v
\tilde{D}^{v}
D~v为
D
~
\tilde{D}
D~中在属性
a
a
a上取值为
a
v
a^{v}
av的样本的子集;
D
~
k
\tilde{D}_{k}
D~k为
D
~
\tilde{D}
D~中标签为
k
k
k的样本子集;
w
x
w_{x}
wx为我们为样本
x
x
x赋予的权重;
(2)我们针对这些样本进行一些统计的计算:
我们记 S u m ( A ) = ∑ x ∈ A w x Sum(A)=\sum_{x\in A}^{}w_{x} Sum(A)=∑x∈Awx
ρ
=
S
u
m
(
D
~
)
/
S
u
m
(
D
)
\rho =Sum(\tilde{D})/Sum(D)
ρ=Sum(D~)/Sum(D) 表示对于属性
a
a
a中无缺失样本的比例;
p
~
k
=
S
u
m
(
D
~
k
)
/
S
u
m
(
D
~
)
\tilde{p}_{k}=Sum(\tilde{D}_{k})/Sum(\tilde{D})
p~k=Sum(D~k)/Sum(D~) 表示对于无缺失样本中第
k
k
k类的比例;
r
~
v
=
S
u
m
(
D
~
v
)
/
S
u
m
(
D
~
)
\tilde{r}_{v}=Sum(\tilde{D}^{v})/Sum(\tilde{D})
r~v=Sum(D~v)/Sum(D~) 表示对于无缺失样本中属性
a
a
a取值为
a
v
a^{v}
av的比例;
(3)修正信息增益的计算式:
回忆一下: G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^{V}\frac{|D^{v}|}{|D|}Ent(D^{v}) Gain(D,a)=Ent(D)−∑v=1V∣D∣∣Dv∣Ent(Dv)
修正后: G a i n ( D , a ) = ρ ( E n t ( D ~ ) − ∑ v = 1 V r ~ v E n t ( D ~ v ) ) Gain(D,a)=\rho (Ent(\tilde{D} )-\sum_{v=1}^{V}\tilde{r} _{v}Ent(\tilde{D} ^{v})) Gain(D,a)=ρ(Ent(D~)−∑v=1Vr~vEnt(D~v))
其中: E n t ( D ~ ) = − ∑ k = 1 ∣ γ ∣ p ~ k log 2 p ~ k Ent(\tilde{D})=-\sum_{k=1}^{|\gamma |}\tilde{p}_{k}\log_{2}{\tilde{p}_{k}} Ent(D~)=−∑k=1∣γ∣p~klog2p~k
我们观察一下这个式子,发现它就是用无缺失值的样本代回原式子,并在前面乘了一个比例
ρ
\rho
ρ,这里的修正因子
ρ
\rho
ρ,实际上是用于调整信息增益的计算,以更准确地反映有缺失值样本下的最佳属性划分。
具体来说,
ρ
\rho
ρ的引入是为了处理在数据集中属性值缺失的样本,确保在决策树构建时不会因为缺失值的存在而偏离最优划分策略。具体实现时,
ρ
\rho
ρ可以有不同的定义方式。
(4)假定我们已经根据新的信息增益计算式找到了划分属性 a a a,考察每一个样本,如果样本 x x x在属性 a a a上没有缺失值,划分入对于的子节点;若 x x x恰好在 a a a属性上有缺失值,则我们将这个 x x x划分入所有的子节点,且更改其权值为 r ~ v ⋅ w x \tilde{r}_{v}\cdot w_{x} r~v⋅wx,可以理解为既分散到每一个子节点中“代办”,同时降低它在某一子节点上的影响,避免对整个构建决策树过程贡献太大。
(5)推广到基尼指数中,完全一致:
基尼值:
G
i
n
i
(
D
)
=
1
−
∑
k
=
1
∣
γ
∣
p
~
k
2
Gini(D)=1-\sum_{k=1}^{|\gamma|}\tilde{p}_{k}^{2}
Gini(D)=1−∑k=1∣γ∣p~k2
基尼指数:
G
i
n
i
‾
i
n
d
e
x
(
D
,
a
)
=
ρ
(
∑
v
=
1
V
r
~
v
G
i
n
i
(
D
v
)
)
Gini\underline{~~}index(D,a)=\rho(\sum_{v=1}^{V}\tilde{r}_{v}Gini(D^{v}))
Gini index(D,a)=ρ(∑v=1Vr~vGini(Dv))