B树

原理

于1970年由R.Bayer和E.mccreight提出，它是一种适合外查找的平衡的多叉树，一棵m阶(m>2)的B树，是一棵平衡的m路平衡搜索树，可以是空树或者满足一下性质：

1. 根节点至少有两个孩子
2. 每个分支节点都包含k-1个关键字和k个孩子，其中 ceil(m/2) ≤ k ≤ m，ceil是向上取整函数
3. 每个叶子节点都包含k-1个关键字，其中 ceil(m/2) ≤ k ≤ m
4. 所有的叶子节点都在同一层
5. 每个节点中的关键字从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域划分，即进行分裂
6. 每个结点的结构为：（n，A0，K1，A1，K2，A2，… ，Kn，An）其中，Ki(1≤i≤n)为关键字，且K[i]<K[i+1](1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于K[i+1]。n为结点中关键字的个数，满足ceil(m/2)-1≤n≤m-1。

我们以一颗3阶的B树为例，模拟它的插入的过程，需要注意在实现时，为了方便我们会为每个结点多开一个空间：即3阶的B树我们会开够3个关键和4个孩子的空间。

B树数据插入的过程为：

1. 如果树为空，直接插入新节点中，该节点为树的根节点
2. 树非空，找待插入元素在树中的插入位置(注意：找到的插入节点位置一定在叶子节点中)
3. 检测是否找到插入位置(假设树中的key唯一，即该元素已经存在时则不插入)
4. 按照插入排序的思想将该元素插入到找到的节点中
5. 检测该节点是否满足B-树的性质：即该节点中的关键字个数是否等于m，如果小于则满足
6. 如果插入后节点不满足B树的性质，需要对该节点进行分裂：

• 申请新节点
• 找到当前插入节点数据的中间位置
• 将该节点中间位置右侧的元素以及其孩子按序搬移到新节点中
• 将中间位置元素以及新节点往该节点的双亲节点中插入，即继续执行步骤4，如果向上已经分裂到根节点的位置，插入结束

关于B树的删除可以参考：B树的删除

对于一棵节点树为n的m阶B树，查找和插入需要进行$lo{g}_{m-1}(n)$到$lo{g}_{m/2}(n)$次比较，其删除操作的时间复杂度为O(log n)。

实现

#include<iostream>
#include<vector>

using namespace std;

static int orderNumber = 3;

template<class T>
struct BTreeNode {
	BTreeNode(int length) 
		:_size(0)
		,_keys(length,T())
		,_parent(nullptr)
		,_children(length+1,nullptr)

	{}

	~BTreeNode()
	{}

	int _size;						//_keys已经使用的大小
	vector<T> _keys;					//存放关键字
	BTreeNode<T>* _parent;				//指向当前结点的父节点
	vector<BTreeNode<T>*> _children;	//存放孩子指针
};

template<class T>
class BTree{
public:
	BTree(int order=orderNumber)
		:_orderNumber(order)
		,_head(nullptr)
	{
		if (order < 2) {
			return;
		}
	}

	~BTree()
	{}

	bool search(T key) {
		BTreeNode<T>* tmp = nullptr;

		return _search(key,tmp);
	}

	bool insert(T key) {
		if (nullptr == _head) {
			_head = new BTreeNode<T>(_orderNumber);
			_head->_keys[(_head->_size)++] = key;
			return true;
		}

		BTreeNode<T>* cur = nullptr;
		if (_search(key,cur)) {
			return false;
		}

		int pos = cur->_size - 1;
		while (pos >= 0 && cur->_keys[pos] > key) {
			cur->_keys[pos + 1] = cur->_keys[pos];
			--pos;
		}
		cur->_keys[pos + 1] = key;
		(cur->_size)++;

		//分裂
		while (cur&&cur->_size == _orderNumber) {
			int mid = (cur->_size)/2;
			BTreeNode<T>* child1 = cur;
			BTreeNode<T>* child2 = new BTreeNode<T>(_orderNumber);
			int i = mid + 1;
			for (; i < cur->_size; ++i) {
				child2->_keys[child2->_size] = cur->_keys[i];
				child2->_children[(child2->_size)++] = cur->_children[i];
				if (cur->_children[i]) {
					cur->_children[i]->_parent = child2;
				}
			}
			child2->_children[child2->_size] = cur->_children[i];
			child1->_size = mid;
			key = child1->_keys[mid];
			if (cur->_children[i]) {
				cur->_children[i]->_parent = child2;
			}
			BTreeNode<T>* parent = cur->_parent;
			if (nullptr == parent) {
				_head = new BTreeNode<T>(_orderNumber);
				parent = _head;
				_head->_keys[0] = key;
				_head->_children[0] = child1;
				_head->_children[1] = child2;
				_head->_size = 1;
				child1->_parent = _head;
				child2->_parent = _head;
				return true;
			}

			for (pos = parent->_size-1; pos >= 0 && parent->_keys[pos] > key;--pos) {
				parent->_keys[pos + 1] = parent->_keys[pos];
				parent->_children[pos + 2] = parent->_children[pos+1];
			}
			parent->_keys[pos+1] = key;
			parent->_children[pos + 2] = child2;
			(parent->_size)++;
			child1->_parent = parent;
			child2->_parent = parent;
			cur = parent;
		}

		return true;
	}
private:
	bool _search(T& key,BTreeNode<T>*& pnode) {
		BTreeNode<T>* cur = _head;
		//采用二分查找快速定位目标值
		while (cur) {
			int left = 0;
			int right = cur->_size-1;
			while (left <= right) {
				int mid = left + (right - left) / 2;
				if (cur->_keys[mid] == key) {
					return true;
				}
				else if (cur->_keys[mid] > key) {
					right = mid - 1;
				}
				else {
					left = mid + 1;
				}
			}
			pnode = cur;
			cur = cur->_children[left];
		}
	}

private:
	int _orderNumber;		//结点阶数
	BTreeNode<T>* _head;	//指向头结点的指针
};

int main() {
	BTree<int> bt;
	bt.insert(53);
	bt.insert(139);
	bt.insert(75);
	bt.insert(49);
	bt.insert(145);
	bt.insert(36);
	bt.insert(101);
	printf("is find %d:%d\n", 36, bt.search(36));
	printf("is find %d:%d\n", 0, bt.search(0));

	return 0;
}

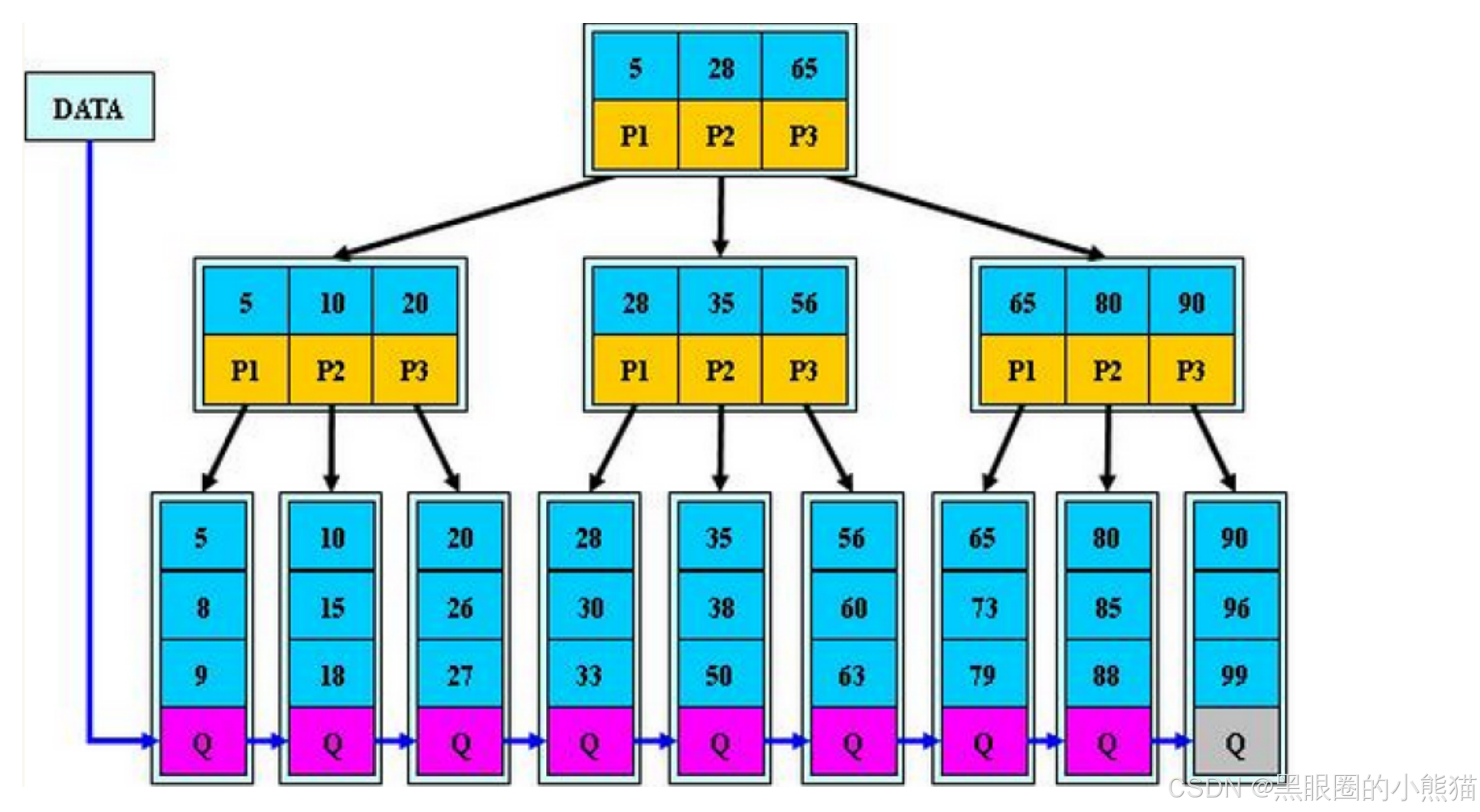
B+树

B+树是B树的变形，是在B树基础上优化的多路平衡搜索树，B+树的规则跟B树基本类似，但是又在B树的基础上做了以下几点改进优化：

1. 分支节点的子树指针与关键字个数相同
2. 分支节点的子树指针p[i]指向关键字值大小在[k[i]，k[i+1])区间之间
3. 所有叶子节点增加一个链接指针链接在一起
4. 所有关键字及其映射数据都在叶子节点出现

B+树的分裂：
当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针，B+树的分裂只影响原结点和父结点，而不会影响兄弟结点。

B+树的特性：

1. 所有关键字都出现在叶子节点的链表中，且链表中的节点都是有序的。
2. 分支节点相当于是叶子节点的索引，叶子节点才是存储数据的数据层。

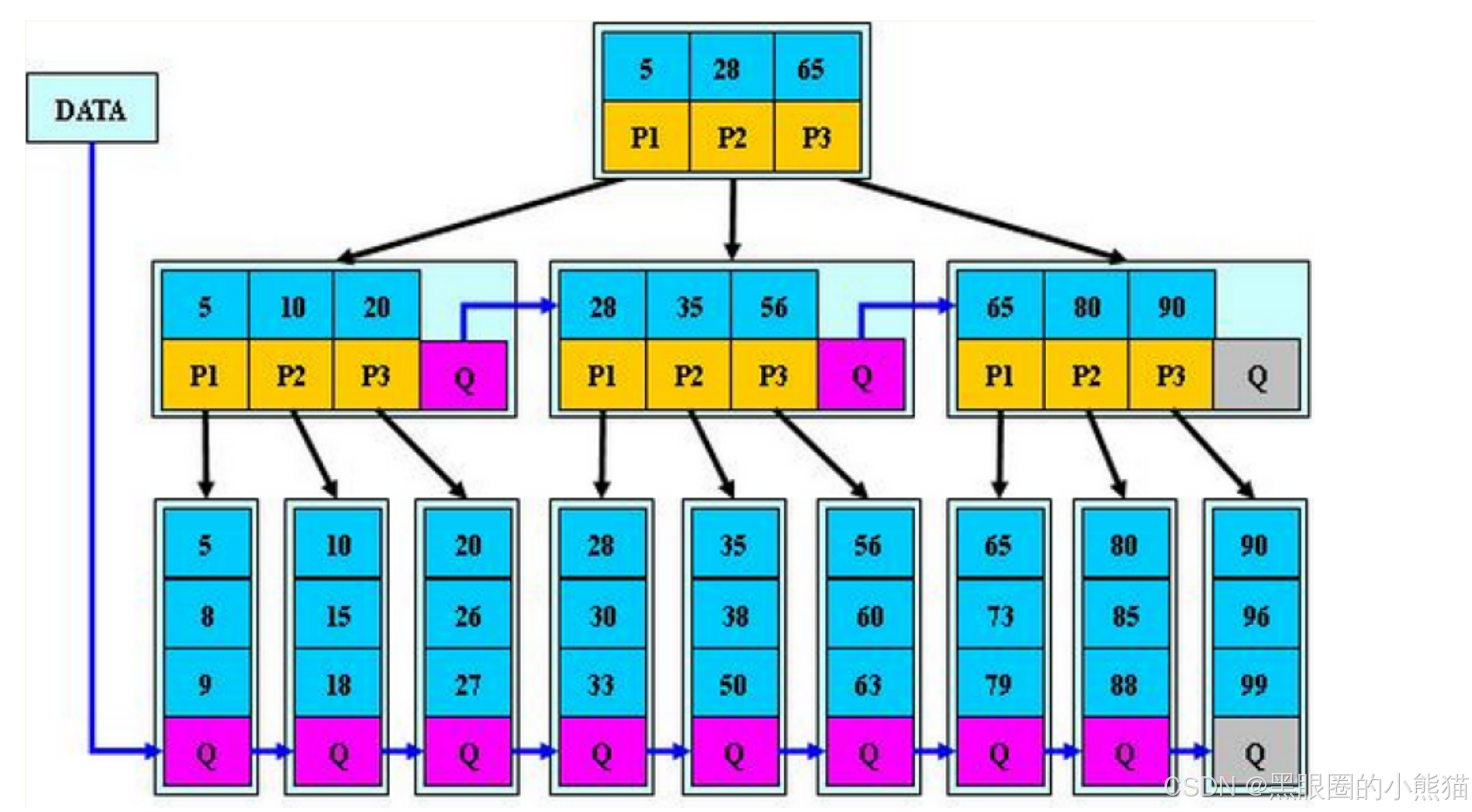
B*树

B*树是B+树的变形，在B+树的非根和非叶子节点再增加指向兄弟节点的指针。

B*树的分裂：
当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针，所以B*树分配新结点的概率比B+树要低，空间使用率更高。

B树系列存在以下缺点：

1. 空间利用率低，消耗高
2. 插入时如果产生分裂、合并结点，需要挪动大量数据
3. 在内存中其查询效率与哈希、平衡树一个量级，优势不明显，因此其适用于外存查询，即所有B树结点都存放在外存当中，每一次读取一个结点都是一次外存访问，由于B树高度很低，查询时就极大减少了外存查询的次数（外存读取数据的速度其实是比较快的，但让磁头定位到要读取数据的区域速度很慢），同时还有cache缓存热数据，进一步减少外存访问。