线性回归
线性回归算法是一种用于预测一个或多个自变量(解释变量)与因变量(响应变量)之间关系的统计方法。这种方法基于线性假设,即因变量是自变量的线性组合加上一个误差项。
基本原理:线性回归的目标是找到一条最佳的直线(或超平面,在多维空间中),使得这条直线上的点到实际数据点的距离(通常是垂直距离)最小。这条最佳直线由系数(也称为权重)和截距确定,系数表示自变量对因变量的影响程度,截距是当所有自变量都为0时因变量的值。
本篇我们来学习如何实现一元线性回归,对于算法模型我们依旧从三个方面来实现它:
- 训练模型
- 测试模型
- 线性回归方程
- 测试实用性
训练模型
- 收集数据
收集到的一元数据:
链接:训练数据
提取码:axwz
- 读取数据
对于表格型数据,用pandas读取处理比较好:
import pandas as pd
data = pd.read_csv("data.csv")
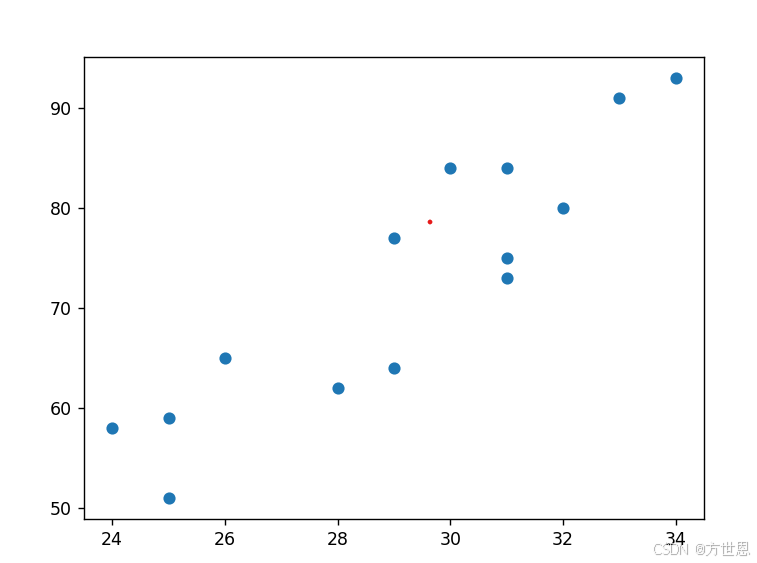
- 绘制散点图
观察数据分布,可能图像无法显示出来,没关系,小bug。
#绘制散点图
from matplotlib import pyplot as plt
plt.scatter(data.广告投入,data.销售额)
plt.show()
- 查看相关系数
查看数据对结果的影响程度,若是影响程度很低的话可以进行特征选择,即将影响小的数据去除掉:
corr = data.corr()
- 建立模型
这里我们使用sklearn中的线性回归模型:
from sklearn.linear_model import LinearRegression
#估计模型参数,建立回归模型
lr = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]
lr.fit(x,y) #训练模型
测试模型
我们就将训练的数据本身放进模型中测试看看,他对本身训练的数据测试结果准确率如何:
result =lr.predict(x) #预测模型结果
score = lr.score(x,y) #模型测试准确率
print(score)
---------------
0.8225092881166945
模型准确率达到要求之后,我们可一将线性模型的回归方程式写出来。
线性回归方程
我们可以得到具体的线性回归表达式:
#round是用来对浮点数进行四舍五入到指定的小数位数
#模型训练完成之后,调试模式下,模型标签中有intercept_,以及coef_参数
a = round(lr.intercept_[0],2) # 查看截距
b = round(lr.coef_[0][0],2) # 查看斜率
print("线性回归模型为:y = {}x + {}.".format(b,a))
------------------------------
线性回归模型为:y = 3.74x + -36.36.
测试实用性
我们将广告投入分别为40,45,50时,放进模型中,求出它们对应的销售额结果:
predict = lr.predict([[40],[45],[50]])
print(predict)
------------------
[[113.15418502]
[131.84361233]
[150.53303965]]
这样我们就完整的实现了一元线性回归。
总结
本篇介绍了如何实现一元线性回归,其中需要注意的是,对于相关系数过小的数据,我们要进行选择调整。