408数据结构
第一章 绪论
第二章 线性表
绪论、线性表选择题做题笔记
第三章 栈、队列和数组
栈、队列和数组选择题做题笔记
第四章 串
文章目录
前言
本篇文章是数据结构第四章:串的内容笔记,讲对数据结构串进行说明与算法补充
一、串的基本知识
1.串的定义
- 串,即字符串,是由零个或者多个字符组成的有限序列。
- 一般记作‘a1,a2,an’,其中,S是串名,单引号(有的地方是双引号)括起来的字符序列是串的值,n为串的长度,即字符串的个数
- n=0时为空串
- 子串:串中任意个连续的字符组成的子序列
- 主串:包含子串的串
- 字符在主串中的位置:字符在串中的序号(从1开始数)
- 子串在主串中的位置:子串的第一个字符在主串中的位置
- 串是一种特殊的线性表,元素之间呈线性关系, 区别在于:线性表中的元素可以是任意类型(一个线性表是一种),而串的元素只能是字符
2.串的基本操作
- 一般来说,对串的基本操作是对子串的操作
赋值操作:把串T赋值为chars
bool strAssign(&T, chars);
复制操作:把串S复制得到串T
bool strCopy(&T, S);
判空操作:若S为空串,则返回true,反之返回FALSE
int strEmpty(S);
求串长,返回串S的元素个数
bool strLength(S);
情况操作,请S清为空串
bool ClearString(&S);
//销毁操作:将串S销毁
bool DestroyString(&S);
串联接:用T返回由S1和S2联接而成的新串
bool Concat(&T, S1, S2);
求子串:用Sub返回串S的第pos个字符起长度为len的子串
bool SubStriing(&Sub, S, pos, len);
定位操作:若主串S中存在与串T值相同的子串,则返回它在主串S中第一次出现的位置,否则函数值为0
bool Index(S, T);
比较操作:若S>T,则返回值>0,以此类推
- 字符串的比较方法:从头开始比较各个字符,当出现第一组不同的字符时,字符对应ASCII码值大的字符大,字符对应的字符串就大
- 若一直相等直到一方穷尽,则长的字符串大
- 只有当两个字符串元素和长度都一模一样是,才是等于
- 两个常见的字符集:(1)ASCII字符集(英文字符)(2)Unicode字符集(中英文)
- 采用不同的编码方式,每个字符所占空间不同,考研中只需要默认每个字符占18即可
bool StrCompare(S, T);
3.串的存储结构
(1)顺序结构
串的定长顺序存储–静态数组实现
#define MAXLEN 255
typedef struct{
char ch[MAXLEN];
int length;
}SString;
-
注意:对于存储长度方式的更新—(1)在数组中专门找一个单元存储长度,有四个版本(2)设置特殊字符代表结束
-
-
优点:(1)若把char[0]用来存储长度,则后面元素的下标与位序能够保持一致
-
缺点:(1)前者的长度只能是0~255(2)后者必须通过遍历才能知道最终长度
串的不定长顺序存储–动态数组实现
typedef struct {
char* ch;//按串长分配存储区,ch指向串的基地址
int length;//串的长度
}HString;
不定长顺序存储的初始化
bool InitHString(HString& S)
{
S.ch = (char*)malloc(MAXLEN * sizeof(char));
S.length = 0;
}
(2)链式结构
串的链式存储
typedef struct StringNode{
char ch;//需要一个字节
struct StringNode* next;//需要四个字节
}StringNode,* String;
- 缺点:存储密度低
对以上缺点做出改进
typedef struct StringNode {
char ch[4];//每个结点存多个字符,若存不完全,可以用特殊字符表示
struct StringNode* next;
}StringNode,* String
- (1)优点:方便进行元素的增加与删除
- (2)缺点:不具备随机存取的特性
(3)基于顺序存储实现基本操作
求子串:用Sub返回串S的第pos个字符起长度为len的子串
bool SubString(SString &Sub, SString S, int pos, int len)
{
//代码健壮性
if (len <= 0 || pos <= 0)
{
return false;
}
if (pos + len - 1 > S.length)
{
return false;
}
//功能实现
for (int i = pos; i <= pos + len; i++)
{
Sub.ch[i - pos + 1] = S.ch[i];
}
Sub.length = len;
return true;
}
定位操作:若主串S中存在与串T值相同的子串,则返回它在主串S中第一次出现的位置,否则函数值为0
第一种思路:从第一个元素开始依次取出S中长度为T.len的子串,再利用判等函数判断,如果相等则搞定,不相等则下一个
int Index_1(SString S, SString T)
{
int i = 1;
int n = strLength(S);
int m = strLength(T);
SString sub;
while (i <= n - m + 1)
{
SubString(sub, S, i, m);
if (StrCompare(sub, T) != 0)
{
++i;
}
else
{
return i;
}
}
return 0;
}
思路二:在主串中直接操作
int Index_2(SString S, SString T)
{
if (T.length == 0)
{
return false;
}
for (int i = 1; i <= S.length - T.length; i++)
{
int tag = 0;
int m = i;
int j = 1;
while(S.ch[m++] == T.ch[j++])
{
if (j == T.length + 1)
{
tag = 1;
break;
}
}
if (tag == 1)
{
return m;
}
}
return 0;
}
- 时间复杂度:O(mn)
比较操作:若S>T,则返回值>0,以此类推
- 字符串的比较方法:从头开始比较各个字符,当出现第一组不同的字符时,字符对应ASCII码值大的字符大,字符对应的字符串就大
- 若一直相等直到一方穷尽,则长的字符串大
- 只有当两个字符串元素和长度都一模一样时,才是等于
- 两个常见的字符集:(1)ASCII字符集(英文字符)(2)Unicode字符集(中英文)
- 采用不同的编码方式,每个字符所占空间不同,考研中只需要默认每个字符占18即可
int StrCompare(SString S, SString T)
{
int i;
for (i = 1; i <= S.length && i <= T.length; i++)
{
if (S.ch[i] > T.ch[i])
{
return 1;
}
else if (S.ch[i] < T.ch[i])
{
return -1;
}
else
{
return 0;
}
}
if (i == S.length && i == T.length)
{
return 0;
}
else if (i == S.length)
{
return -1;
}
else
{
return 1;
}
}
4.字符串的模式匹配算法
- 什么是模式匹配:在主串中找到与模式串相同的子串,并返回其所在位置
(1)朴素模式匹配算法
- 什么是朴素模式匹配算法:找出主串中长度与模式串相同的子串,并进行对比,直到找到一个完全匹配的子串或者所有子串都不匹配为止
- 其实就是上面的定位算法,只不过定位算法找的是子串,一定可以找到,而模式匹配算法找的是模式串,未必可以找到
(2)KPM算法(数据结构算法难度榜top3)
- 为什么叫KMP算法?
- 答:发明者名字为D.E.Knuth和J.H.M.orris和V.R.Pratt,各取一个字母得到KMP
- 由来:对朴素模式匹配算法的优化
- 原理:充分利用模式串的信息,使得每次失配后,根据失配的位置调整下一个进行匹配的子串以及模式串的位置,而不是像朴素算法一样,无脑下一个
- 核心:利用next数组存储失配位置与下一个位置的对应关系
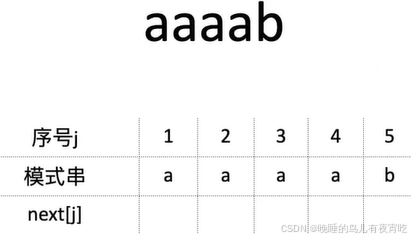
next数组的练习
-
自己分类讨论一个匹配串在各个位置失配后,模式串可以移动的最小位移可能
-
(1)当第一位置失配时,无论上面模式串都是j指向0然后i++,j++
-
(2)当第二个位置失配时,无论上面模式串都是j=1
-
(3)当第三个以及后面的位置失配时,j依次只往左移动一个,看看前面的会不会匹配,会的话就刚好只需要移动到当前位置,否则继续,直到移动到j=1
-
注:看书时发现的两个问题
-
问题一:有时下标是从-1开始的,即next[0]=-1;next[1]=0,需要根据题目判断是哪种
-
问题二:对于原始next数组的求法,尽管本人认为直接根据理解去手算出来就好,但下面有一个科学的方法解释过程
(1)概念补充: -
前缀:一个字符串除了最后一个字符外的子串
-
后缀:一个字符串除了第一个字符外的子串
-
部分匹配值:字符串的前缀和后缀的最长相等部分的长度
(2)举例说明(以‘ababa’为例) -
对于前一个字符’a’:前后缀均为空集,因此对于匹配值为0
-
对于前两个字符ab",前缀为‘a’,后缀为‘b’,匹配值仍然为0
-
对于前三个字符’aba’,前缀为‘ab’,后缀为‘ba’,交集子串为‘b’,因此匹配值为1
-
对于前四个字符’aban’,前缀为‘aba’,后缀为‘bab’,交集子串为‘ba’,因此匹配值为2
-
对于前五个字符‘ababa’,前缀为‘abab’,后缀为‘baba’,交集子串为‘bab’,因此匹配值为3
得到的部分匹配值为00123
(3)处理 -
显然!这跟我们按照理解写出来的next数组肯定是不一样的,因此这个匹配值并不是数组的内容,数组的内容应该是:1+匹配值(除了第一个数字恒为0),即0,1+0,1+0,1+1,1+2,即01123
-
这个方法就了解一下就好了,过程烦琐,真不如直接靠理解手算出来的简单
next数组的优化(我称为二阶next数组)
-
刚好就是刚刚的那个想法,有一种->next = ->next->next的感觉,比较合理
-
优化原理:利用已知第i个位置和匹配串的第j个位置不同,而原始next数组的next[j]的字符刚好和第j个位置的字符一样!!!那就没必要,直接优化到下一个next就好了,跳过一次失配
-
优化之前是:0 1 2 3 4
-
优化之后是:0 0 0 0 4
得到优化数组的代码
bool renew(int arr[],SString S)
{
int nextval[100];
nextval[1] = 0;
for (int j = 2; j < S.length; j++)
{
if (S.ch[arr[j]] == S.ch[j])
{
nextval[j] = arr[arr[j]];
}
else
{
nextval[j] = arr[j];
}
}
return true;
}
KMP算法
int Index_KMP(SString S, SString T, int next[])
{
int i = 1;
int j = 1;
while (i <= S.length && j <= T.length)
{
if (j == 0 || S.ch[i] == T.ch[j])
{
++i;
++j;
}
else
{
j = next[j];
}
}
if (j > T.length)
{
return i - T.length;
}
else
{
return 0;
}
}
- 最坏时间复杂度:O(m+n)(求next数组复杂度为O(m),模式匹配过程最坏时间复杂度为O(n))
总结
可能是有两年c的基础,本质学起来并没有太多难点,难度top3的匹配算法学起来并没有那么困难,甚至在他讲之前,本能的也可以想到朴素算法和优化next数组,因此难度并不高!