摘要
摘要—分布式协同同步定位与地图构建(DCSLAM)中的后端模块需要在分布式设置下求解一个非线性位姿图优(PGO)问题,也称为SE(d)同步。现有的大多数分布式图优化算法采用简单的序列化划分方案,这可能导致由于每个机器人地理位置的不同而产生不平衡的子图维度,从而增加额外的通信负载。此外,当前的黎曼优化算法性能仍有进一步加速的空间。本文提出了一种新型的分布式位姿图优化算法,该算法结合了多级划分和加速的黎曼优化方法。首先,我们采用多级图划分算法对简单的位姿图进行预处理,以构造一个平衡的优化问题。其次,受加速坐标下降法的启发,我们设计了一种改进的黎曼块坐标下降(IRBCD)算法,并且所得到的临界点是全局最优的。最后,我们评估了四种常见图划分方法对子图间相关性的影响,发现最高优先级划分方案具有最佳的划分性能。同时,我们通过仿真实验定量证明了所提算法在性能上优于现有的最先进的分布式位姿图优化协议。
一、介绍
近年,随着多机器人系统在如野外搜索与救援 [1]、区域覆盖 [2] 和环境探索 [3] 等领域的广泛应用,因其高效的协作、强大的泛化能力和灵活的重新配置能力,这些系统取得了显著进展。对于这些复杂任务,协同定位与地图构建(CSLAM)是一项关键技术,使得每个机器人能够协同估计其位姿,并在大规模未知环境中构建全局地图,从而提升多机器人系统的自主性和智能性。根据是否存在中央计算节点,CSLAM系统可分为集中式和分布式两种类型 [4]。分布式CSLAM仅依赖于机器人之间的局部感知、计算与通信,从而使得其具有更好的扩展性 [5]。分布式位姿图优化(DPGO)是从分布式CSLAM系统的后端模块抽象出来的核心数学模型。该模型涉及每个机器人在SE(d)空间中基于最大似然估计来解决最小二乘问题,目标是解决机器人间回环估计的位姿与单个机器人相对测量(含噪声)之间的匹配问题。在这种情况下,位姿图中的每个节点可以被视为由旋转变量和平移变量组成的变量块。地理测距被用来衡量位姿间的不一致性,因此该最小二乘问题属于黎曼流形优化问题 [6]。然而,对于这一大规模分布式非线性优化问题,仍然存在一些待解决的问题。现有的分布式图优化算法大多依赖于数据测量的所有权,在位姿图上进行简单的序列划分,而未充分利用图本身的特性,如连通性、稀疏性和变量之间的耦合度,如图1(a)所示。这导致每个机器人构建的优化子问题维度不平衡,从而增加了通信负担,降低了算法的效率。此外,仍有空间进一步提升算法的高效协作、强大泛化能力和灵活重新配置性能。为了解决上述问题,本文提出了一种新型的分布式图优化算法,该算法结合了多级图划分与加速方法。我们应用多级图划分算法,将原始位姿图中耦合度高的节点合并,然后将压缩后的图划分为多个块,并进行适当的精细调整。图划分方法使得每个机器人获得一个平衡的位姿子图,从而为后续的分布式优化提供良好的初始化(见图1(b))。
图1. (a) 顺序划分和 (b) 图划分的表示。我们用 T1, …, T8 表示位姿变量块,用实线黑线表示机器人内部的回环闭合,用虚线红线表示机器人之间的相对位姿关系。(a) 和 (b) 分别展示了通过顺序划分和图划分后每个机器人获得的子图。
由于分布式位姿图优化问题的非凸性,我们将其重新表述为低秩凸松弛(LRCR)形式,并使用所提出的改进黎曼块坐标下降(IRBCD)方法求解。IRBCD是由Nesterov提出的加速坐标下降法(ACDM)的一种扩展,它不依赖于目标函数的Lipschitz常数,并引入了广义动量项以加速计算。本文证明了IRBCD算法能够收敛到全局最优的一级临界点。
此外,我们比较了四种属于卡尔斯鲁厄高质量划分(KaHIP)框架的图划分方法(分别命名为Strong、Eco、Fast和Highest)[8][9],并在标准数据集上进行了实验。实验结果表明,Highest策略在所有划分策略中取得了最佳的划分质量。与此同时,与现有的最先进的RBCD和RBCD++ [10]方法相比,IRBCD方法提升了精度和收敛速度。因此,所提的分布式位姿图优化算法不仅能减少多机器人系统网络中的通信负担,还能提高优化解的质量。
贡献:本文致力于通过多机器人协作解决分布式位姿图优化问题。主要贡献如下:
- 我们实现了多级图划分方法,以构建分布式位姿图优化中的平衡优化子问题。
- 受ACDM启发,我们提出了IRBCD算法,并证明该算法能够收敛到全局最优的一级临界点。
符号说明:我们定义
Sym
(
h
)
\operatorname{Sym}(h)
Sym(h) 和
Sym
(
h
)
+
\operatorname{Sym}(h)^{+}
Sym(h)+ 分别为
h
×
h
h \times h
h×h 对称实矩阵和对称半正定实矩阵的集合,并用
I
h
I_{h}
Ih 表示大小为
h
h
h 的单位矩阵。对于矩阵 X,我们使用
X
(
i
,
j
)
X_{(i, j)}
X(i,j) 来索引它的第
(
i
,
j
)
(i, j)
(i,j) 个元素。设
det
(
X
)
\operatorname{det}(X)
det(X) 和
tr
(
X
)
\text{tr}(X)
tr(X) 分别为方阵 X 的行列式和迹。给定两个矩阵
A
∈
R
m
×
n
A \in \mathbb{R}^{m \times n}
A∈Rm×n 和
B
∈
R
m
×
n
B \in \mathbb{R}^{m \times n}
B∈Rm×n,我们赋予标准内积
⟨
A
,
B
⟩
=
tr
(
A
T
B
)
\langle A, B \rangle = \text{tr}(A^{T}B)
⟨A,B⟩=tr(ATB)。符号
∥
⋅
∥
F
\|\cdot\|_{F}
∥⋅∥F 表示矩阵的弗罗贝尼乌斯范数。我们还定义
[
n
]
=
{
1
,
2
,
…
,
n
}
[n] = \{1, 2, \ldots, n\}
[n]={1,2,…,n}。
本文中经常出现的矩阵流形包括特殊正交群 SO(d):
{
R
∈
R
d
×
d
∣
R
T
R
=
I
d
,
det
(
R
)
=
1
}
\{R \in \mathbb{R}^{d \times d} | R^T R = I_{d}, \det(R) = 1\}
{R∈Rd×d∣RTR=Id,det(R)=1},特殊欧几里得群 SE(d):
{
(
R
,
T
)
∈
R
d
×
(
d
+
1
)
∣
R
∈
S
O
(
d
)
,
T
∈
R
d
}
\{(R, T) \in \mathbb{R}^{d \times (d+1)} | R \in SO(d), T \in \mathbb{R}^d\}
{(R,T)∈Rd×(d+1)∣R∈SO(d),T∈Rd},以及
s
t
i
e
f
e
l
m
a
n
i
f
o
l
d
stiefel manifold
stiefelmanifold流形
S
t
(
r
,
d
)
St(r, d)
St(r,d):
{
R
∈
R
r
×
d
∣
R
T
R
=
I
d
}
\{R \in \mathbb{R}^{r \times d} | R^T R = I_d\}
{R∈Rr×d∣RTR=Id}。
论文结构:本文的其余部分安排如下。第二部分回顾了与本研究相关的文献。第三部分给出了DPGO问题的数学描述,并介绍了算法的整体框架。最后,第四部分进行实验评估,第五部分提供了结论。
二、相关工作
尽管SLAM社区已经进行了许多研究,但本节只回顾与我们工作最相关的研究:位姿图优化和图划分。
A. 位姿图优化
随着多智能体系统的发展,协同SLAM已成为一个实际的方案。根据是否存在中央协调器,CSLAM系统后端的位姿图优化问题可以被描述为集中式PGO或分布式PGO。在集中式PGO中,一种具有优越性能的先进方法是Rosen等人提出的具有可验证正确性保证的SE-Sync方法[11]、[12]。这个核心思想也被应用于其他工作,例如描述全局旋转同步的低秩优化模型[13]。此外,Briales等人[14]简化了SE(d)同步模型,并将状态的搜索空间扩展到Cartan运动群,在特定场景中实现了更快的收敛。
分布式PGO问题也得到了研究。例如,Choudhary等人[15]提出了一种两阶段的高斯-塞德尔方法,该方法通过解耦旋转和平移分量来迭代恢复姿态,但这种方法受到初始化质量的极大影响,不能保证收敛到一阶临界点。为了解决这个问题,Fan等人[16]采用了一种主要化-最小化(MM)方法来解决分布式PGO问题,从而确保其下降序列能够收敛到一阶临界点。Tian等人[17]还设计了一种基于黎曼梯度优化的异步并行分布式算法,并在有限通信延迟下分析了其收敛性。受SE-Sync启发,他们进一步提出了一种基于黎曼块坐标下降(RBCD)的可验证分布式位姿图优化方法,并证明了在一定条件下它可以收敛到全局一阶临界点[10]。还有一些工作考虑了机器人的动态模型,并基于反馈控制理论设计了分布式共识算法,例如Cristofalo等人提出的GEOD算法[18]。在实际应用中,[19]提出了Kimera-Multi,这是一个分布式多机器人协同SLAM系统,它能够在有限的通信带宽下稳健地识别和拒绝错误的回环闭合检测,并实时构建全局一致的3D语义网格模型。然而,应该强调的是,上述所有方法都是基于每个机器人的局部姿态信息执行顺序划分操作,没有充分考虑位姿图的结构特征。
B. 图划分
图分割问题在组合优化领域是传统且困难的。例如,最小-最大平衡图分割问题属于NP难问题类[20]。特征分解[21]和最大流最小割[22]是解决图划分问题的两种常用方法。然而,这些方法要么计算成本高,要么不适用于动态变化的图,要么在处理大规模图时难以并行化。然而,这些方法要么计算复杂度较高,要么忽略了平衡约束条件,因此不适合处理大规模图划分问题。相比之下,启发式、多级和进化算法[23][24]是相对复杂的方法,其中多级图划分算法在计算速度和划分质量上具有明显优势[25]。Xuet al. [26] 提出了一种用于分布式PGO的在线流图划分方法,并开发了一个平衡的分布式图优化(BDPGO)框架,该框架在机器人故障情况下经过了鲁棒性验证。然而,BDPGO对图的动态变化高度敏感,且其划分效果通常依赖于图数据的输入顺序。
三. 数学模型与算法设计
在本节中,我们提出了一种新型的分布式位姿图优化算法(参见算法1中的伪代码)。首先,我们考虑在执行多级图划分操作后,为分布式位姿图优化问题建立数学模型。在对子问题进行适当的半定松弛和Burer-Monteiro(BM)分解后,得到低秩SDP问题。最后,应用改进的黎曼分布式块坐标下降方法(IRBCD)来求解该问题。图2展示了集中式PGO问题、DPGO(问题1-3)、IRBCD算法和本节中描述的定理1之间的内在关系。
A. DPGO问题表述
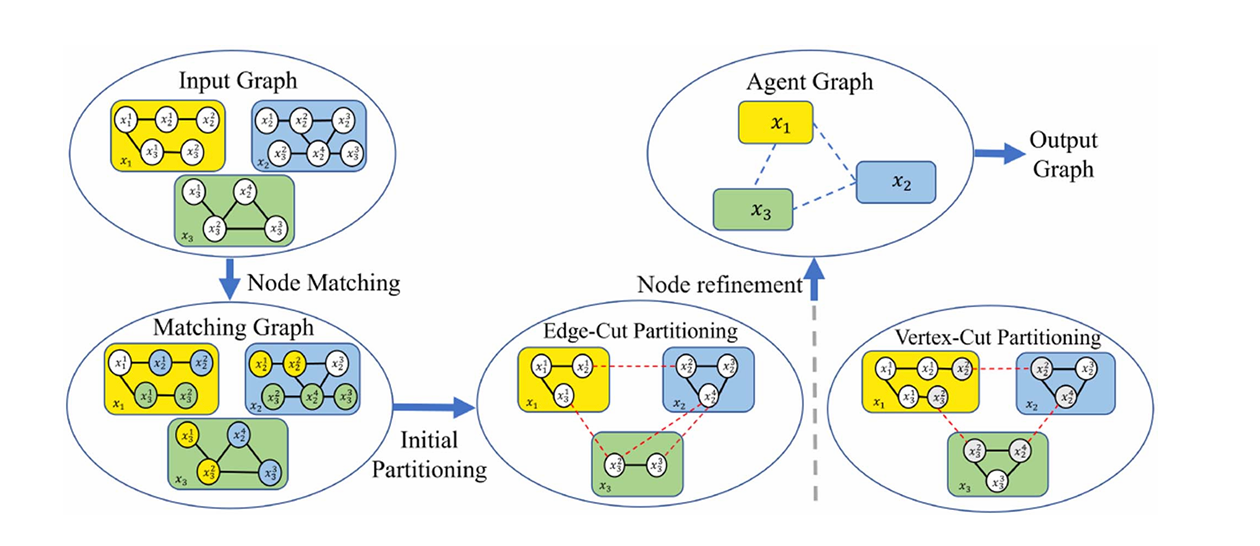
图3. 多级图划分过程。整个过程分为三个阶段:1)根据评估函数匹配具有高耦合度的节点;2)使用边切割划分或顶点切割划分等方法将原始图分割成与机器人数量相等的平衡子图;3)对子图进行精细调整以生成代理级位姿图。
考虑一个由N个机器人组成的多机器人系统,每个机器人只能感知局部信息。PGO的目的是从不精确的相对测量中估计每个机器人的运动轨迹。为了解决这个问题,我们将其表述为一个有向图 G = ( V , E ) \mathcal{G}=(\mathcal{V},\mathcal{E}) G=(V,E),其中 V = [ n ] \mathcal{V}=[n] V=[n] 中的每个节点对应于机器人 i ∈ [ N ] i\in[N] i∈[N] 在其 τ \tau τ 关键帧的未知姿态 x i τ = ( R i τ , T i τ ) ∈ S E ( d ) x_{i}^{\tau}=\left(R_{i}^{\tau}, T_{i}^{\tau}\right)\in S E(d) xiτ=(Riτ,Tiτ)∈SE(d),而 E ⊂ V × V \mathcal{E}\subset\mathcal{V}\times\mathcal{V} E⊂V×V 中的每条边对应于机器人 i ∈ [ N ] i\in[N] i∈[N] 的关键帧 τ \tau τ 和机器人 j ∈ [ N ] j\in[N] j∈[N] 的关键帧 s s s 之间的相对测量 x ~ i τ j s = ( R ~ i τ j s , T ~ i τ j s ) ∈ S E ( d ) \widetilde{x}_{i_{\tau}}^{j_{s}}=(\widetilde{R}_{i_{\tau}}^{j_{s}},\widetilde{T}_{i_{\tau}}^{j_{s}})\in S E(d) x iτjs=(R iτjs,T iτjs)∈SE(d)。不失一般性,假设 G \mathcal{G} G 是弱连通的。假设测量模型满足以下关系:
R ~ i τ j s = ( R i τ ) T R j s R ϵ , ( 1 ) \widetilde{R}^{j_{s}}_{i_{\tau}}=(R^{\tau}_{i})^{T}R^{s}_{j}R_{\epsilon},\qquad(1) R iτjs=(Riτ)TRjsRϵ,(1)
T ~ i τ j s = ( R i τ ) T ( T i τ − T j s ) + T ϵ , ( 2 ) \widetilde{T}_{i_{\tau}}^{j_{s}}=(R_{i}^{\tau})^{T}(T_{i}^{\tau}-T_{j}^{s})+T_{\epsilon},\qquad(2) T iτjs=(Riτ)T(Tiτ−Tjs)+Tϵ,(2)
其中旋转噪声 R ϵ R_{\epsilon} Rϵ 和平移噪声 T ϵ T_{\epsilon} Tϵ 分别服从各向同性朗之万分布 Langevin ( I d , w R ) \left(I_{d}, w_{R}\right) (Id,wR) 和多变量高斯分布 N ( 0 , w T ) \mathcal{N}\left(0, w_{T}\right) N(0,wT)[11]。在测量模型(1)-(2)下,我们通过最大似然估计表述了一个集中式PGO问题:
∑ ( x i τ , x j s ) ∈ E w R 2 ∥ R j s − R i τ R ~ i τ j s ∥ F 2 ( 3 a ) \sum_{(x_{i}^{\tau}, x_{j}^{s}) \in \mathcal{E}} w_{R}^{2} \left\| R_{j}^{s} - R_{i}^{\tau} \tilde{R}_{i_{\tau}}^{j_{s}} \right\|_{F}^{2} \qquad (3a) (xiτ,xjs)∈E∑wR2 Rjs−RiτR~iτjs F2(3a)
+ w T 2 ∥ T j s − T i τ − R i τ T ~ i τ j s ∥ 2 2 ( 3 b ) + w_{T}^{2} \left\| T_{j}^{s} - T_{i}^{\tau} - R_{i}^{\tau} \tilde{T}_{i_{\tau}}^{j_{s}} \right\|_{2}^{2} \qquad (3b) +wT2 Tjs−Tiτ−RiτT~iτjs 22(3b)
为了促进多个机器人协同解决上述问题,我们对图
G
\mathcal{G}
G 进行多层次图划分,将位姿图划分为几个平衡的子图。
如图3所示,我们在粗化阶段根据边权重评估函数选择要合并的节点,然后通过边割或顶点割划分,将位姿图
G
\mathcal{G}
G 分为几个平衡的子图,数量与机器人的数量相等,最后细化每个子图以生成N个不相交的集合 X = (
a
1
,
a
2
,
…
,
a
N
a_1, a_2, \ldots, a_N
a1,a2,…,aN)。值得一提的是,每个机器人
i
∈
[
N
]
i \in [N]
i∈[N] 的状态空间不仅包含其局部姿态信息,还可能提取来自其他机器人的姿态信息,即
x
i
=
(
x
i
1
,
…
,
x
j
τ
,
…
,
x
k
l
i
)
,
∀
i
,
j
,
k
∈
[
N
]
,
∀
τ
∈
[
l
i
]
,
(
4
)
x_{i}=\left(x_{i}^{1},\ldots, x_{j}^{\tau},\ldots, x_{k}^{l_{i}}\right),\forall i, j, k\in[N],\forall\tau\in\left[l_{i}\right],\quad(4)
xi=(xi1,…,xjτ,…,xkli),∀i,j,k∈[N],∀τ∈[li],(4)
其中 [ l i ] \left[l_{i}\right] [li] 表示在图划分后第 i i i 个机器人所拥有的所有关键帧姿态的索引集合。
因此,在图划分之后,我们得到了如下的分布式位姿图优化问题:
问题 1(DPGO)
f
(
X
)
=
∑
i
=
1
N
f
i
(
x
i
)
(
5
a
)
f(X) = \sum_{i=1}^{N} f_{i}(x_{i}) \qquad (5a)
f(X)=i=1∑Nfi(xi)(5a)
f i ( x i ) = ∑ ( x i τ , x j s ) ∈ E i w R 2 ∥ R j s − R i τ R ~ i τ j s ∥ F 2 + w T 2 ∥ T j s − T i τ − R i τ T ~ i τ j s ∥ 2 2 ( 5 b ) f_i(x_i) = \sum_{(x_i^\tau, x_j^s) \in \mathcal{E}_i} w_R^2 \left\| R_j^s - R_i^\tau \tilde{R}_{i_\tau}^{j_s} \right\|_F^2 + w_T^2 \left\| T_j^s - T_i^\tau - R_i^\tau \tilde{T}_{i_\tau}^{j_s} \right\|_2^2 \qquad (5b) fi(xi)=(xiτ,xjs)∈Ei∑wR2 Rjs−RiτR~iτjs F2+wT2 Tjs−Tiτ−RiτT~iτjs 22(5b)
x i = ( x i 1 , … , x j τ , … , x k l i ) ( 5 c ) x_i = (x_i^1, \ldots, x_j^\tau, \ldots, x_k^{l_i}) \qquad (5c) xi=(xi1,…,xjτ,…,xkli)(5c)
x i τ , x j s ∈ S E ( d ) x_{i}^{\tau}, x_{j}^{s} \in SE(d) xiτ,xjs∈SE(d),对于所有 i , j , k ∈ [ N ] i, j, k \in [N] i,j,k∈[N] 和所有 τ , s ∈ [ l i ] ( 5 d ) \tau, s \in [l_i] \qquad (5d) τ,s∈[li](5d) 。
其中 f i f_{i} fi 是每个机器人构建的图优化子问题, E i \mathcal{E}_{i} Ei 是第 i i i 个机器人拥有的局部位姿图的边集,这意味着问题1中的目标函数可以被重写为:函数 f ( X ) = ⟨ G , X T X ⟩ f(X) = \left\langle G, X^{T} X \right\rangle f(X)=⟨G,XTX⟩,其中 G ∈ Sym ( n ( d + 1 ) ) G \in \operatorname{Sym}(n(d+1)) G∈Sym(n(d+1)) 是由所有相对测量和权重 ( w R 2 , w T 2 ) \left(w_{R}^{2}, w_{T}^{2}\right) (wR2,wT2) 形成的块矩阵。设 Z = X T X ∈ Sym ( ( d + 1 ) × n ) + Z = X^{T} X \in \operatorname{Sym}((d+1) \times n)^{+} Z=XTX∈Sym((d+1)×n)+,然后问题1的约束条件被重新表述为:
Z ⪰ 0 , ( 6 a ) Z \succeq 0,\qquad (6a) Z⪰0,(6a)
rank ( Z ) = d , ( 6 b ) \operatorname{rank}(Z) = d,\qquad (6b) rank(Z)=d,(6b)
Z i i ( 1 : d , 1 : d ) = I d , ( 6 c ) Z_{i i(1: d, 1: d)} = I_d,\qquad (6c) Zii(1:d,1:d)=Id,(6c)
det ( Z i i ( 1 : d , 1 : d ) ) = 1 , ( 6 d ) \operatorname{det}\left(Z_{i i(1: d, 1: d)}\right) = 1, \qquad (6d) det(Zii(1:d,1:d))=1,(6d)
问题1的优化问题可以表述为:
min Z ∈ Sym ( ( d + 1 ) × n ) + f ( Z ) = ⟨ G , Z ⟩ ( 7 a ) \min_{Z \in \operatorname{Sym}((d+1) \times n)^{+}} f(Z) = \langle G, Z \rangle (7a) Z∈Sym((d+1)×n)+minf(Z)=⟨G,Z⟩(7a)
Z
i
i
(
1
:
d
,
1
:
d
)
=
I
d
,对于所有
i
∈
V
(
7
b
)
Z_{i i(1: d, 1: d)} = I_d,对于所有 i \in \mathcal{V} \qquad (7b)
Zii(1:d,1:d)=Id,对于所有i∈V(7b)
对于某些
Y
∈
R
r
×
(
d
+
1
)
n
(
r
≪
n
)
Y \in \mathbb{R}^{r \times (d+1) n}(r \ll n)
Y∈Rr×(d+1)n(r≪n),每个
Z
Z
Z 可以分解为对称低秩解
Z
=
Y
T
Y
Z = Y^T Y
Z=YTY。因此,问题2可以转化为具有低秩约束的凸优化问题:
问题3(P2的秩限制问题)
f
(
Y
)
=
⟨
G
,
Y
T
Y
⟩
,
(
8
a
)
f(Y) = \left\langle G, Y^{T} Y \right\rangle,(8a)
f(Y)=⟨G,YTY⟩,(8a)
Y
=
(
Y
1
,
T
1
,
…
,
Y
n
,
T
n
)
∈
(
S
t
(
r
,
d
)
×
R
)
n
,
(
8
b
)
Y = \left(Y_{1}, T_{1}, \ldots, Y_{n}, T_{n}\right) \in (St(r, d) \times \mathbb{R})^{n},\qquad (8b)
Y=(Y1,T1,…,Yn,Tn)∈(St(r,d)×R)n,(8b)
其中 Y i Y_i Yi 属于Stiefel流形空间而不是 S O ( d ) SO(d) SO(d),对于所有 i ∈ V i \in \mathcal{V} i∈V。
最终,我们可以从问题3的一阶临界点 Y ∗ Y^* Y∗ 恢复SDP松弛问题2的解 Z ⋆ Z^{\star} Z⋆。将问题2的最优值记为 f SDP ⋆ f_{\text{SDP}}^{\star} fSDP⋆。考虑到问题1的最优解为 f ⋆ f^{\star} f⋆,其函数值 f ( X ) f(X) f(X) 满足以下不等式:
f ( X ) − f ∗ ≤ f ( X ) − f SDP ⋆ , ( 9 ) f(X) - f^* \leq f(X) - f_{\text{SDP}}^\star, \qquad (9) f(X)−f∗≤f(X)−fSDP⋆,(9)
当且仅当 f ∗ = f SDP ⋆ f^{*} = f_{\text{SDP}}^{\star} f∗=fSDP⋆ 时,等式成立。因此,公式(9)保证了问题2产生的解在问题1中的全局最优性。
注1:在多机器人系统中执行图划分任务时,有一个中心节点负责接收所有位姿图结构信息,而不是原始测量数据。利用这些信息,它随后继续为其余群体进行划分。
B. 加速黎曼优化算法
问题3本质上是一个在定义为 M ( r , d ) : = ( S t ( r , d ) × R d ) n \mathcal{M}(r, d):=\left(St(r, d) \times \mathbb{R}^d\right)^n M(r,d):=(St(r,d)×Rd)n 的乘积流形空间中的大规模优化问题,因此设计一个加速黎曼优化算法至关重要。
N e s t e r o v Nesterov Nesterov 提出了一种用于欧几里得空间中无约束大规模最小化问题的加速坐标下降方法 A C D M ACDM ACDM,其收敛速度为 O ( 1 / k 2 ) \mathcal{O}\left(1/k^2\right) O(1/k2),其中 k k k 是迭代次数[7]。ACDM 采用合适的多步策略来更新解向量序列 { Y k } ∈ R n \left\{Y^k\right\} \in \mathbb{R}^n {Yk}∈Rn,估计解向量序列 { P k } ∈ R n \left\{P^k\right\} \in \mathbb{R}^n {Pk}∈Rn 和梯度序列 { V k } ∈ R n \left\{V^k\right\} \in \mathbb{R}^n {Vk}∈Rn 如下所示:
P k = α k V k + ( 1 − α k ) Y k , ( 10 ) P^k = \alpha_k V^k + (1 - \alpha_k) Y^k, \qquad (10) Pk=αkVk+(1−αk)Yk,(10)
Y k + 1 = P k − 1 L i k ∇ f i ( P k ) , ( 11 ) Y^{k+1} = P^k - \frac{1}{L_{i_k}} \nabla f_i(P^k), \qquad (11) Yk+1=Pk−Lik1∇fi(Pk),(11)
V k + 1 = β k V k + ( 1 − β k ) P k − γ k L i k ∇ f i ( P k ) , ( 12 ) V^{k+1} = \beta_k V^k + (1 - \beta_k) P^k - \frac{\gamma_k}{L_{i_k}} \nabla f_i(P^k), \qquad (12) Vk+1=βkVk+(1−βk)Pk−Likγk∇fi(Pk),(12)
其中 L i k L_{i_k} Lik 是对应于坐标块 i k i_k ik 的梯度的 L i p s c h i t z Lipschitz Lipschitz常数, ∇ f i ( ⋅ ) \nabla f_i(\cdot) ∇fi(⋅) 是欧几里得空间中局部目标函数的梯度。辅助变量序列 { α k } , { β k } , { γ k } \left\{\alpha_k\right\}, \left\{\beta_k\right\}, \left\{\gamma_k\right\} {αk},{βk},{γk} 具有耦合方程关系:
γ k 2 − γ k n = β k γ k n 1 − α k α k . ( 13 ) \gamma_k^2 - \frac{\gamma_k}{n} = \frac{\beta_k \gamma_k}{n} \frac{1 - \alpha_k}{\alpha_k}. \qquad (13) γk2−nγk=nβkγkαk1−αk.(13)
我们将这种加速算法扩展到流形空间,并称之为改进的黎曼块坐标下降
I
R
B
C
D
IRBCD
IRBCD。在算法1中,根据以下四个方面对ACDM进行了修改。
1). 为了保证IRBCD算法生成的迭代点被限制在流形空间内,算法1中的第12行和第16行引入了一个适当的投影算子
Proj
M
(
⋅
)
\operatorname{Proj}_{\mathcal{M}}(\cdot)
ProjM(⋅),将欧几里得空间中的点
Y
k
,
P
k
,
V
k
Y^k, P^k, V^k
Yk,Pk,Vk 映射回
M
(
r
,
d
)
\mathcal{M}(r, d)
M(r,d)。
2). 与公式(11)不同,本文采用的块坐标下降方法通过最小化目标函数(8)生成所选坐标块 i k ∈ [ N ] i_k \in [N] ik∈[N] 的迭代序列 { Y i k k } \left\{Y_{i_k}^k\right\} {Yikk}:
Y i k k + 1 = arg min Y i k ∈ M i f i k ( P i k k ) , ( 14 ) Y_{i_k}^{k+1} = \underset{Y_{i_k} \in \mathcal{M}_i}{\arg\min} f_{i_k}(P_{i_k}^k), \qquad (14) Yikk+1=Yik∈Miargminfik(Pikk),(14)
其中 M i : = ( S t ( r , d ) × R d ) l i \mathcal{M}_i := \left(St(r, d) \times \mathbb{R}^d\right)^{l_i} Mi:=(St(r,d)×Rd)li 表示机器人 i ∈ [ N ] i \in [N] i∈[N] 姿态的搜索空间。
3). 受广义动量加速方法[27]的启发,我们在更新 V k + 1 V^{k+1} Vk+1 时使用迭代变量 P k P^k Pk 和 Y k + 1 Y^{k+1} Yk+1 之间的残差作为动量项,从而避免了在原始方法中计算涉及Lipschitz常数的梯度范数的必要性。具体来说,
V k + 1 = Proj M ( β k V k + ( 1 − β k ) P k + γ k ( Y k + 1 − P k ) ) . ( 15 ) \begin{align*}V^{k+1} = & \operatorname{Proj}_{\mathcal{M}}\left(\beta_k V^k + (1 - \beta_k) P^k + \gamma_k (Y^{k+1} - P^k)\right).\\ & \end{align*} \qquad (15) Vk+1=ProjM(βkVk+(1−βk)Pk+γk(Yk+1−Pk)).(15)
直观地说,如果目标参数持续朝最优方向移动,那么在相同方向上添加动量可以加速算法收敛到稳定点。此外,使用动量信息还可以帮助算法逐渐摆脱鞍点并避免停滞。
4). 我们的程序利用了另一种加速机制:自适应重启策略。重启标准的形态如下:
f ( Y k + 1 ) > f ( Y k ) + c 1 ∥ grad f ( Y k ) ∥ 2 ( 16 ) f(Y^{k+1}) > f(Y^k) + c_1 \|\operatorname{grad} f(Y^k)\|^2 \qquad (16) f(Yk+1)>f(Yk)+c1∥gradf(Yk)∥2(16)
其中 c 1 c_{1} c1 是重启常数。基本思想是在算法执行过程中,如果目标函数的值没有显示出下降趋势,就使用当前迭代点作为初始值来重启算法,以寻找新的最优解,以确保IRBCD算法能够在流形空间上收敛。
注2: C a y l e y Cayley Cayley变换是 S t i e f e l Stiefel Stiefel流形上常用的回缩操作。假设存在 X ∈ S t ( n , p ) X \in St(n, p) X∈St(n,p), U ∈ R n × p U \in \mathbb{R}^{n \times p} U∈Rn×p 在X上的正交投影表达式为:
Proj X ( U ) = U − X X T U + U T X 2 . ( 17 ) \operatorname{Proj}_X(U) = U - X \frac{X^T U + U^T X}{2}. \qquad (17) ProjX(U)=U−X2XTU+UTX.(17)
注3: I R B C D IRBCD IRBCD技术在多机器人网络中使用同步更新机制运行。序列 { P k } \left\{P^k\right\} {Pk}(第12行)和 { V k } \left\{V^k\right\} {Vk}(第16行)的更新仅使用局部信息和投影算子,而目标序列 { Y k } \left\{Y^k\right\} {Yk}(第14行)的迭代需要机器人邻居的共享信息 { P k } \left\{P^k\right\} {Pk}。此外,为了决定算法是否执行重启操作,还必须收集所有机器人的目标函数的黎曼梯度信息。
C. 收敛性分析
我们以与 I R B C D IRBCD IRBCD收敛性相关的主要结论结束本节。
定理1:设 f f f为优化问题(8)的光滑函数,并假设 f f f的黎曼梯度满足Lipschitz型条件(参见[10],引理1)。设 { Y k } \left\{Y^k\right\} {Yk}由算法1生成,其中包含重启常数 c 1 c_1 c1和特定于块的常数 λ \lambda λ。则,
lim k → ∞ ∥ grad f ( Y k ) ∥ = 0. ( 18 ) \lim_{k\rightarrow\infty}\left\|\operatorname{grad} f\left(Y^k\right)\right\|=0.\qquad(18) k→∞lim gradf(Yk) =0.(18)
这意味着当 k → ∞ k\rightarrow\infty k→∞时, Y k Y^k Yk是一阶稳定点(参见[28],命题4.6)。
证明:为了证明算法1的一阶收敛性,我们只关注IRBCD中序列 { Y k } \left\{Y^k\right\} {Yk}的更新。我们根据是否触发自适应重启操作讨论两种情况。
考虑第一种情况,当函数值在时间k和时间 k + 1 ( k ≥ 0 ) k+1(k\geq 0) k+1(k≥0)之间的差距不满足重启要求时,
f ( Y k ) − f ( Y k + 1 ) ≥ c 1 ∥ grad f ( Y k ) ∥ 2 . ( 19 ) f\left(Y^k\right)-f\left(Y^{k+1}\right)\geq c_{1}\left\|\operatorname{grad} f\left(Y^k\right)\right\|^{2}.\qquad(19) f(Yk)−f(Yk+1)≥c1 gradf(Yk) 2.(19)
由(19)可知, f ( Y k ) ≥ f ( Y k + 1 ) f\left(Y^k\right)\geq f\left(Y^{k+1}\right) f(Yk)≥f(Yk+1),这意味着全局函数迭代方向不增加。
对于所有 M ≥ 1 M\geq 1 M≥1,我们结合(19)和标准的望远镜求和论证得到以下不等式:
f ( Y 0 ) − f ( Y M ) ≥ c 1 ∑ k = 0 M − 1 ∥ grad f ( Y k ) ∥ 2 . ( 20 ) f\left(Y^0\right)-f\left(Y^M\right)\geq c_1\sum_{k=0}^{M-1}\left\|\operatorname{grad} f\left(Y^k\right)\right\|^2.\quad(20) f(Y0)−f(YM)≥c1k=0∑M−1 gradf(Yk) 2.(20)
假设f是全局下界的,即存在 f low ∈ R f_{\text{low}} \in \mathbb{R} flow∈R 使得对于所有k, f ( Y k ) ≥ f low f(Y^k) \geq f_{\text{low}} f(Yk)≥flow。那么,当M趋向于无穷大时我们可以看到:
∑ k = 0 ∞ ∥ grad f ( Y k ) ∥ 2 ≤ f ( Y 0 ) − f low c 1 < + ∞ , ( 21 ) \sum_{k=0}^{\infty}\left\|\operatorname{grad} f(Y^k)\right\|^2 \leq \frac{f(Y^0) - f_{\text{low}}}{c_1} < +\infty, \qquad (21) k=0∑∞ gradf(Yk) 2≤c1f(Y0)−flow<+∞,(21)
这表明 ∥ grad f ( Y k ) ∥ → 0 \left\|\operatorname{grad} f(Y^k)\right\| \rightarrow 0 gradf(Yk) →0 当 k → ∞ k \rightarrow \infty k→∞。
在第二种情况,当满足重启条件时。根据[10]中的引理2,可以得出以下界限关系:
f ( Y k ) − f ( Y k + 1 ) ≥ λ 4 ∥ grad f ( Y k ) ∥ 2 . ( 22 ) f(Y^k) - f(Y^{k+1}) \geq \frac{\lambda}{4}\left\|\operatorname{grad} f(Y^k)\right\|^2. \qquad (22) f(Yk)−f(Yk+1)≥4λ gradf(Yk) 2.(22)
类似于第一种情况的证明过程,可以证明结论(18)。
四.实验
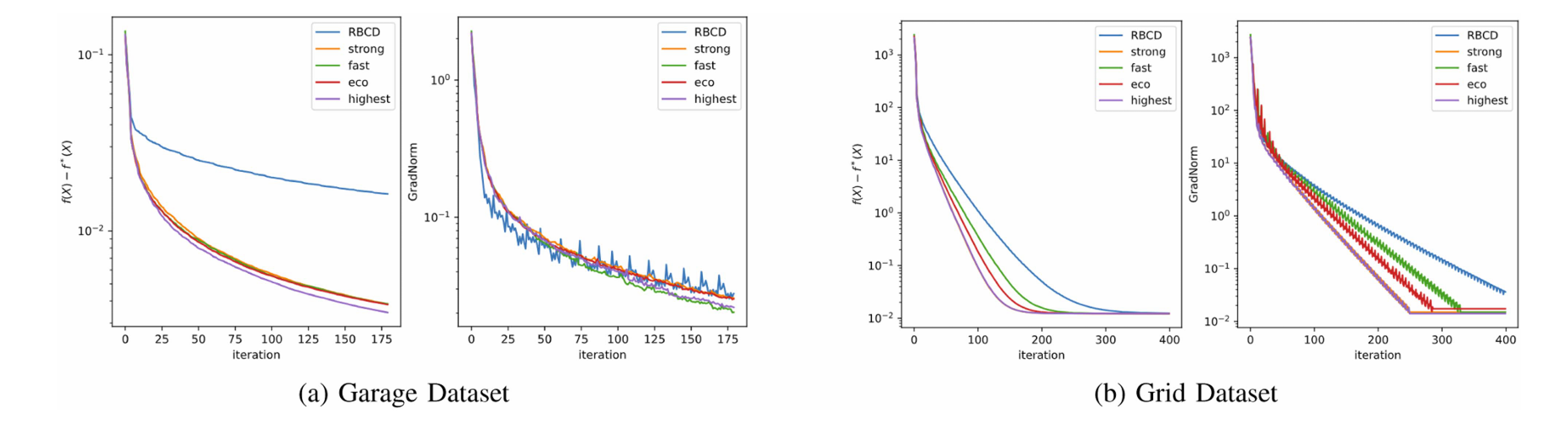
图 4. 不同图划分方法对优化算法性能的影响。我们将四种多级图划分方法分别与 RBCD 算法结合,并在 Garage 和 Grid 数据集上进行实验。同时,将基于顺序图划分的 RBCD 算法作为基准。
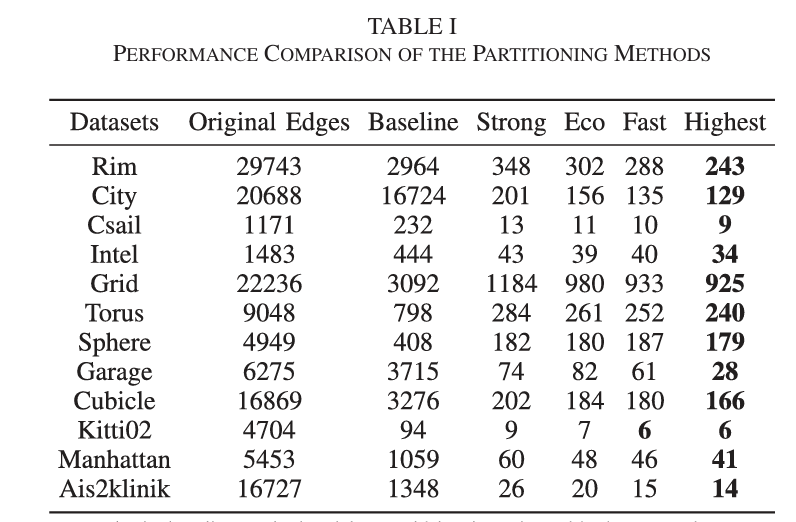
我们对基线方法和四种多级图划分策略在基准数据集上进行了应用,并计算了各个va块之间的切割边数。基线方法是顺序划分,而四种图策略分别是强、经济、快速和最高。加粗的值突出显示了在12个数据集中,“最高”方法的分割性能是最优的。
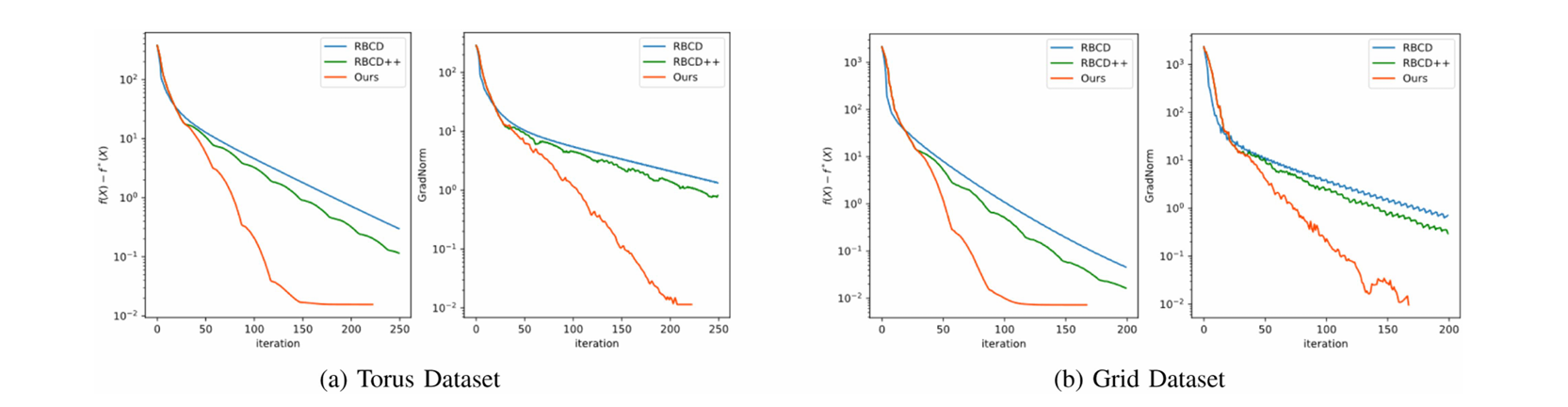
图5. IRBCD算法(我们的)与RBCD、RBCD++优化算法的性能比较。Torus和Grid数据集被用来测试三种分布式优化算法的性能,并且获得了它们的收敛结果。
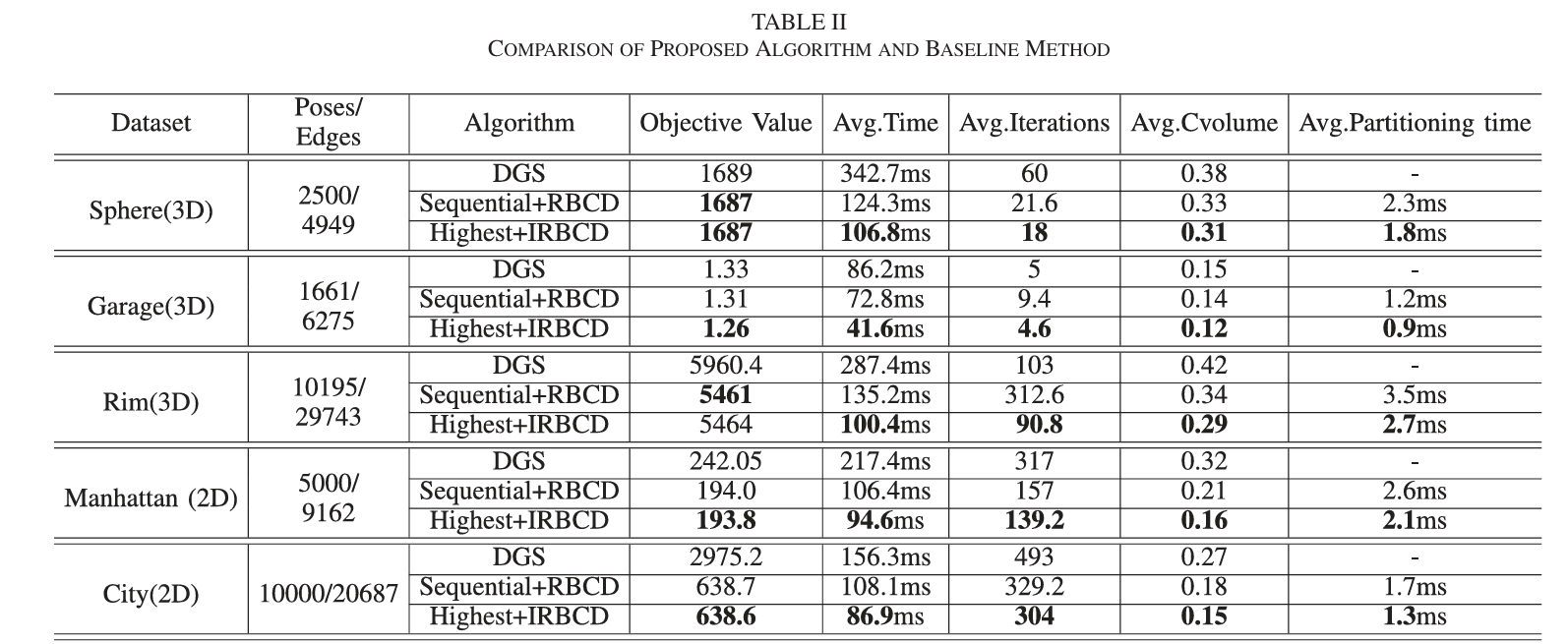
“平均迭代次数”是指每个机器人的平均迭代次数。“平均通信量”是通信量因子的平均值。“平均划分时间”是每个关键帧图划分的平均时间。
加粗的值强调了这种方法在特定方面(如目标值、平均时间等)优于其他方法。
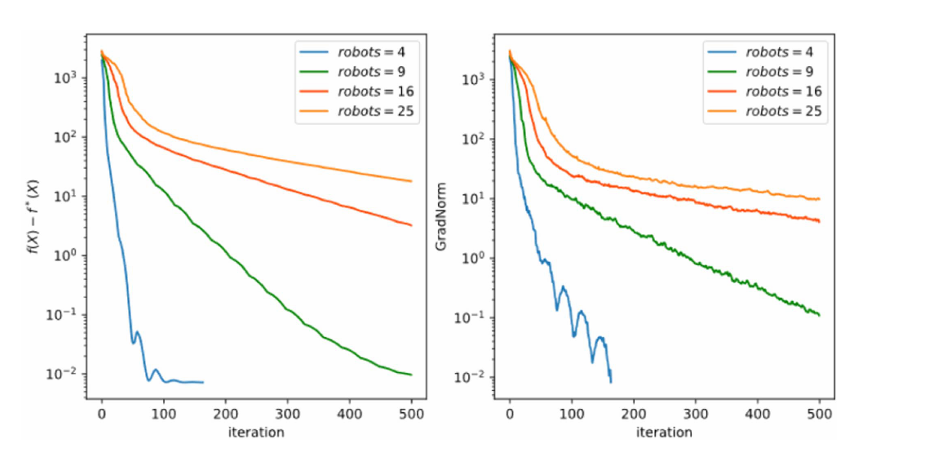
图6. 不同数量的机器人对完整优化算法性能的影响。测试的虚拟机器人数量分别为4、9、16和25。