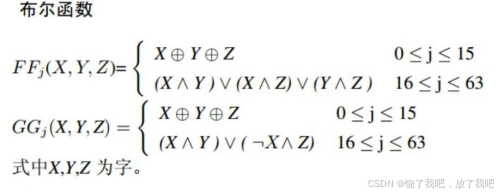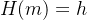一、实验目的
SM3 杂凑算法与实现
(1)理解 Hash 函数的计算原理和特点
(2)掌握 SM3 杂凑算法原理
(3)编程实现 SM3 杂凑算法
硬件:运行 Windows 操作系统的计算机
软件:Python
二、方案设计
背景
SM3 是我国采用的一种密码散列函数标准,由国家密码管理局于2010 年12 月17日发布。《SM3 密码杂凑算法》于2012 年发布为密码行业标准(GM/T 0004-2012),2016年发布为国家标准(GB/T 32905-2016)。2018 年10 月,含有我国《SM3 密码杂凑算法》的ISO/IEC 10118-3:2018《信息安全技术杂凑函数第3 部分:专用杂凑函数》第4 版由ISO 发布,《SM3 密码杂凑算法》正式称为国际标准。在商用密码体系中,SM3 主要用于数字签名及验证、消息认证码生成及验证、随机数生成等,其算法公开。据国家密码管理局表示,其安全性及效率与SHA-256 相当。在实现上,SM3 密码杂凑算法运算速率高、灵活灵用、支持跨平台的高效实现,具有较好的实现效能。
原理
1、术语与定义:
(1)比特串 bit string
由 0 和 1 组成的二进制数字序列。
(2)大端 big-endian
数据在内存中的一种表示格式,规定左边为高有效位,右边为低有效位。数的高阶字节放在存储器的低地址,数的低阶字节放在存储器的高地址。
(3)消息 message
任意有限长度的比特串。本文本中消息作为杂凑算法的输入数据。
(4)杂凑值 hash value
杂凑算法作用于消息后输出的特定长度的比特串。本文本中的杂凑值长度为 256 比 特。
(5)字 word
长度为 32 位的比特串
2、符号
3.常量与函数
4、算法描述
SM3 密码杂凑算法基于 Merkle-Damgard 结构,杂凑函数 H 可将一个任意有限比特长度的消息 m 压缩到某一固定长度为 n 比特的杂凑值 h,即
SM3 密码杂凑算法是对长度为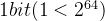
消息填充:
假设消息 m 的长度为1比特。首先将比特“ 1”添加到消息的末尾,再添加 k 个“ 0”,k 是满足 的最小的正整数。然后再添加一个 64 位的比特串,该比特串是长度
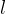
消息扩展:
迭代压缩:
迭代过程
压缩函数
三、方案实现
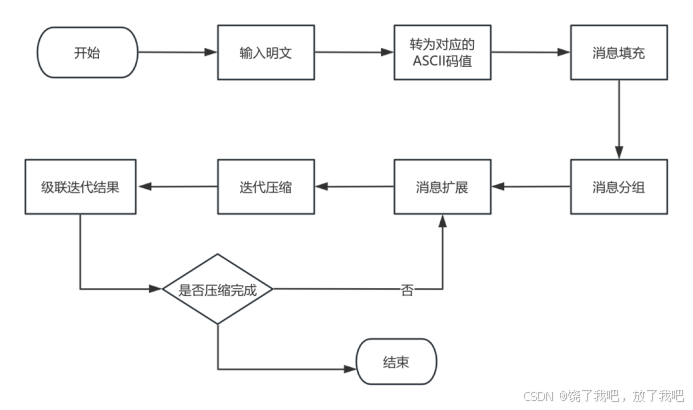
1.流程图
图1 SM3算法实现流程图
2.主要函数
def pad_message(message):——实现消息填充。由于先添加1,对应于16进制即为\x80,再填0补全至448mod 512,最后在加入消息长度的2进制比特串。
def SM3_CF(V, B):——实现压缩迭代。初始V为IV默认值,每次返回与前一次V的级联结果。按照SM3的算法流程实现压缩和迭代,其中,消息扩展也在本环节中进行,
def or_16(A, B):——实现两个字符串按位与或,返回整数C。
def LS(X, n):——实现循环左移。将左右个移动,再连接起来,实现循环。
3.代码实现
import binascii
import re
# SM3的初始向量
IV = [
0x7380166F, 0x4914B2B9, 0x172442D7, 0xDA8A0600,
0xA96F30BC, 0x163138AA, 0xE38DEE4D, 0xB0FB0E4E
]
# 布尔函数FFj
def FF(X, Y, Z, j):
if j < 16:
return X ^ Y ^ Z
else:
return (X & Y) | (X & Z) | (Y & Z)
# 置换函数
def P0(X):
return X ^ LS(X, 9) ^ LS(X, 17)
def P1(X):
return X ^ LS(X, 15) ^ LS(X, 23)
# 循环左移
def LS(X, n):
return ((X << n) & 0xFFFFFFFF) | (X >> (32 - n))
# 布尔函数GGj
def GG(X, Y, Z, j):
if j < 16:
return X ^ Y ^ Z
else:
return (X & Y) | (~X & Z)
# 消息填充函数
def pad_message(message):
mlen1 = len(message)
mlen = mlen1
message += b'\x80'
mlen += 1
while mlen % 64 != 56:
message += b'\x00'
mlen += 1
message += (mlen1 * 8).to_bytes(8, 'big')
return message
# SM3压缩函数
def SM3_CF(V, B, k):
W = [0] * 68
W_ = [0] * 64
for i in range(16):
W[i] = int.from_bytes(B[i*4:i*4+4], 'big')
for i in range(16, 68):
W[i] = P1(W[i-16] ^ W[i-9] ^ LS(W[i-3], 15)) ^ LS(W[i-13], 7) ^ W[i-6]
for i in range(64):
W_[i] = W[i] ^ W[i+4]
for i in range(0, len(W), 4):
print(' '.join(hex(value) for value in W[i:i+4]))
A, B, C, D, E, F, G, H = V
for i in range(64):
SS1 = LS((LS(A, 12) + E + LS(T(i), i % 32)) & 0xFFFFFFFF, 7)
SS2 = SS1 ^ LS(A, 12)
TT1 = (FF(A, B, C, i) + D + SS2 + W_[i]) & 0xFFFFFFFF
TT2 = (GG(E, F, G, i) + H + SS1 + W[i]) & 0xFFFFFFFF
D = C
C = LS(B, 9)
B = A
A = TT1
H = G
G = LS(F, 19)
F = E
E = P0(TT2)
print(
f"Step {i+1} - A: {A:08X}, B: {B:08X}, C: {C:08X}, D: {D:08X}, E: {E:08X}, F: {F:08X}, G: {G:08X}, H: {H:08X}")
return A, B, C, D, E, F, G, H
# T函数
def T(j):
if j < 16:
return 0x79CC4519
else:
return 0x7A879D8A
# SM3哈希函数
def string_to_ascii(s):
return [ord(c) for c in s]
def or_16(A, B):
A = int(A, 16)
B = int(B, 16)
C = A ^ B
C = '{:08x}'.format(C)
return C
# SM3哈希函数
def SM3(message):
ascii_values = string_to_ascii(message)
message_bytes = bytes(ascii_values)
padded_message = pad_message(message_bytes)
result = ''
for i in IV:
result += '{:08x}'.format(i)
V = IV.copy()
for i in range(len(padded_message) // 64):
B = padded_message[i*64:(i+1)*64]
V = SM3_CF(V, B, i)
hex_string1 = binascii.hexlify(B).decode()
formatted_hex_string1 = re.sub(r'(.{8})', r'\1 ', hex_string1)
print(
f"Extended Message at Step {i+1}: {formatted_hex_string1}")
all = ''
for iii in V:
all += '{:08x}'.format(iii)
result = or_16(all, result)
return result
# 示例
message = 'abc'
hash_value = SM3(message)
formatted_hex_string2 = re.sub(r'(.{8})', r'\1 ', hash_value)
print("Hash Value:", formatted_hex_string2)
四、数据分析
1. SM3执行结果
测试数据:abc
中间数据:
填充完的消息:
图2 SM3算法填充后的消息结果图
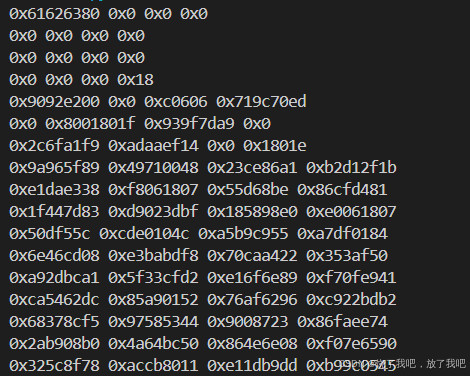
扩展后的消息:
图3 SM3算法扩展后的消息结果图
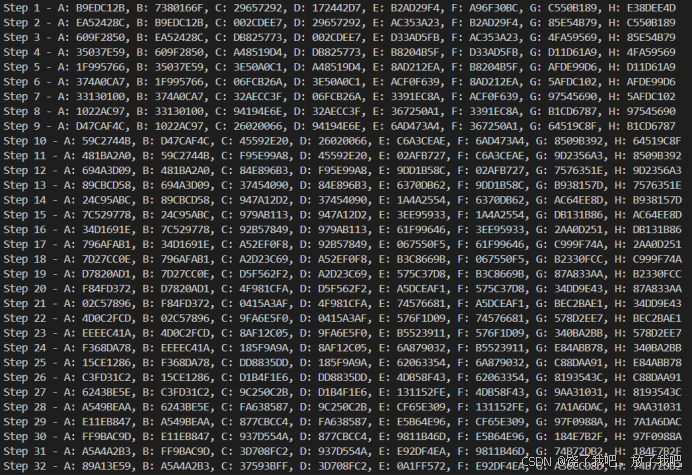
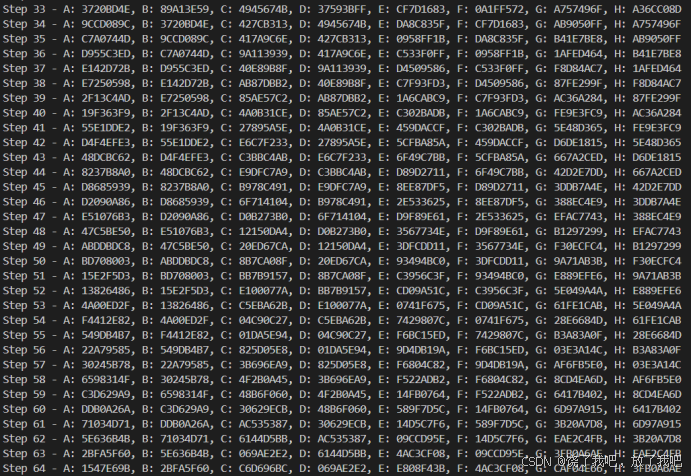
每一轮的V:
图5 SM3算法中间数据V的数据结果图
杂凑值:
图4 SM3算法杂凑结果图
符合测试样例,算法执行成功。
2.SM3的安全性分析
2.1 优势
高抗碰撞性:SM3算法经过严格的安全性分析和测试,具有较高的抗碰撞性和抗预处理性,能够有效地保护数据的完整性和真实性。这意味着已知一个哈希结果,构建出具有相同结果的输入数据的难度非常大。
与国际标准相当:SM3算法在结构上与SHA-256相似,但通过增加多种新的设计技术,使其在安全性和效率上具有优势。尽管SM3算法的字典库远小于SHA-256,但其破解难度更大,因此在实际应用中具有更高的安全性。
抵抗常见攻击:SM3算法被设计为能够抵抗各种常见的密码分析攻击,包括碰撞攻击和预像攻击。虽然某些版本的SM3算法可能存在漏洞,如原根攻击和伪碰撞攻击,但完整的SM3算法仍然具有非常高的安全性。
高于其他算法:SM3算法的安全性要高于MD5算法和SHA-1算法。这是因为这些算法已经被证明存在严重的安全缺陷,而SM3算法则在设计和实现上更加精细和安全。
广泛应用和认可:SM3算法已经被46类重要的经济行业规范所采纳,并且在数字认证、金融密码系统、国家电网、社会保障信息系统等领域得到了广泛应用。这进一步证明了其在实际应用中的高安全性和可靠性。
SM3算法在安全性方面表现优异,能够有效抵抗各种常见的密码分析攻击,并且在国际标准上具有相当的水平。其高抗碰撞性、高效性以及广泛的应用领域,使其成为一个值得信赖的密码学哈希函数。
2.2风险
SM3算法作为一种密码杂凑函数,自2012年发布为行业标准,并在2016年成为国家标准。然而,近年来对其安全性进行了深入研究,发现了一些潜在的漏洞。
2021年2月,蜚语安全在对客户产品进行安全代码审计时,发现其依赖的微信小程序sm-crypto 开源NodeJS国密算法库中的SM3算法实现存在问题。进一步的研究表明,对于带消息填充的29步SM3算法,可以通过中间相遇攻击技术进行原根攻击和伪碰撞攻击。具体来说,从第1步开始的带消息填充的29步SM3算法的原根攻击时间复杂度为2254,而伪碰撞攻击时间复杂度为2125。这说明该算法不能有效抵抗这些攻击。
长度扩展攻击是指针对某些允许包含额外信息的加密散列函数的攻击手段。对于满足以下条件的散列函数,都可以作为攻击对象:① 加密前将待加密的明文按一定规则填充到固定长度(例如512或1024比特)的倍数;② 按照该规则进行加密。虽然证据中没有直接提到SM3算法是否受到长度扩展攻击,但考虑到其设计特性,这种攻击可能也会影响SM3的安全性。
五、思考与总结
1.请简述SM3与MD5、SHA-1的异同。
答:
SM3、MD5和SHA-1均属于散列函数,它们的主要功能是接收任意长度的数据输入,并输出固定长度的散列值,这个散列值通常被称为“消息摘要”。这些算法广泛应用于数据完整性验证和密码学领域。
相同点:
数据完整性: 三者都用于确保数据在传输或存储过程中未被篡改。
固定长度输出: 不论输入数据的大小,输出的散列值长度是固定的。
雪崩效应: 输入数据的任何微小变化都会导致输出散列值的巨大变化。
不可逆: 从散列值不能推导出原始输入数据。
不同点:
设计标准: SM3是中国国家密码管理局制定的密码散列算法标准,而MD5和SHA-1是由国际组织或标准制定。
安全性: MD5和SHA-1由于设计时间较早,已存在已知的安全问题和攻击方法,如碰撞攻击。SM3设计时考虑了这些安全问题,采用了更复杂的结构来提高抗攻击能力。
输出长度: MD5产生128位的散列值,SHA-1产生160位的散列值,而SM3产生256位的散列值,提供了更高的安全边际。
算法结构: SM3使用了更复杂的数学结构和算法流程,包括用于置乱消息的置换函数和用于压缩消息的布尔函数,这使得其对抵抗密码分析攻击更为强固。
2.实验过程中还遇到了什么问题,如何解决的?通过该实验有何收获?
答:
问题1:在消息填充模块,算法实现时将mlen用于直接累加计数,导致原数据长度丢失。
方案:设置一个变量,记录初始长度,在结尾将原mlen替换。
问题2:在得到V后,如何输出杂凑函数值,如何级联?
方案:属于概念未明晰,不知如何进行级联。第一轮的输出应该与初始向量IV级联,而后以此类推。而且,需要注意的是,在级联后,需要按位进行与或操作。
收获:
通过本次实验,我深入理解了SM3算法的原理和特点,尤其掌握了SM3算法的结构和实现方法,编程实践增强了我对该算法的理解并提升了我的技术能力,让我对密码学领域有了更深刻的认识。