数据结构 - 悦读

什么是数据结构

数据的逻辑结构以及存储结构及操作(数据的运算)

1.1 数据

数据：不再是单纯的数字，而是类似集合的概念

数据元素：是数据的基本单位，由若干个数据项组成

数据项：数据的最小单位，描述数据元素有用信息

数据元素又叫为节点

例如：

计算机处理的对象(数据)已不再是单纯的数值：

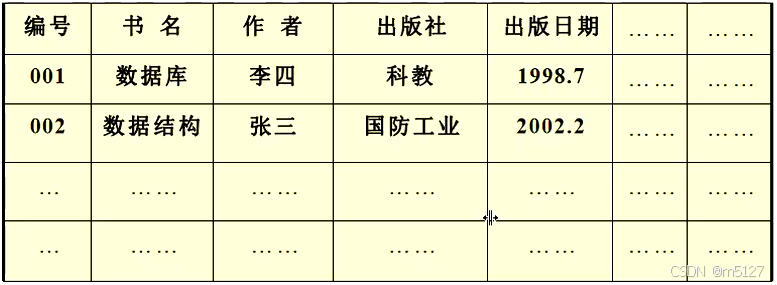
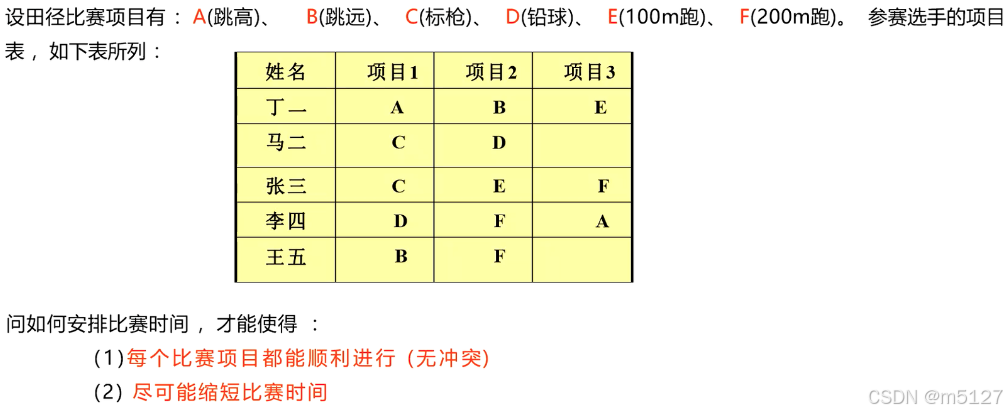
图书管理中的数据，如下表所列:

1.2 逻辑结构

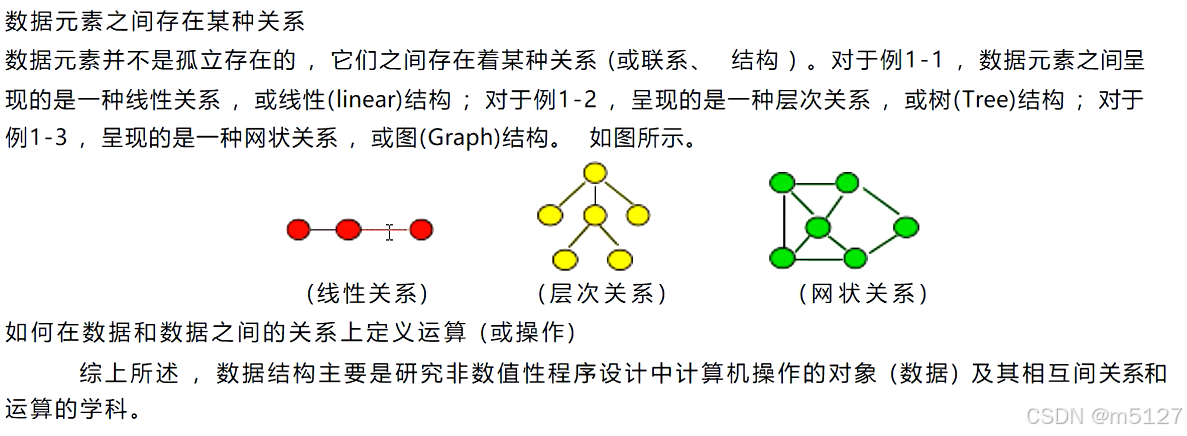
数据元素并不是孤立存在的，它们之间存在着某种关系(或联系、结构)。元素和元素之间的关系：

线性关系

逻辑结构：线性结构

特点：一对一

线性结构：顺序表、链表、栈、队列

层次关系

逻辑结构：树形结构

特点：一对多

树形结构：二叉树

网状关系

逻辑结构：图状结构

特点：多对多

图状结构：图

例题：

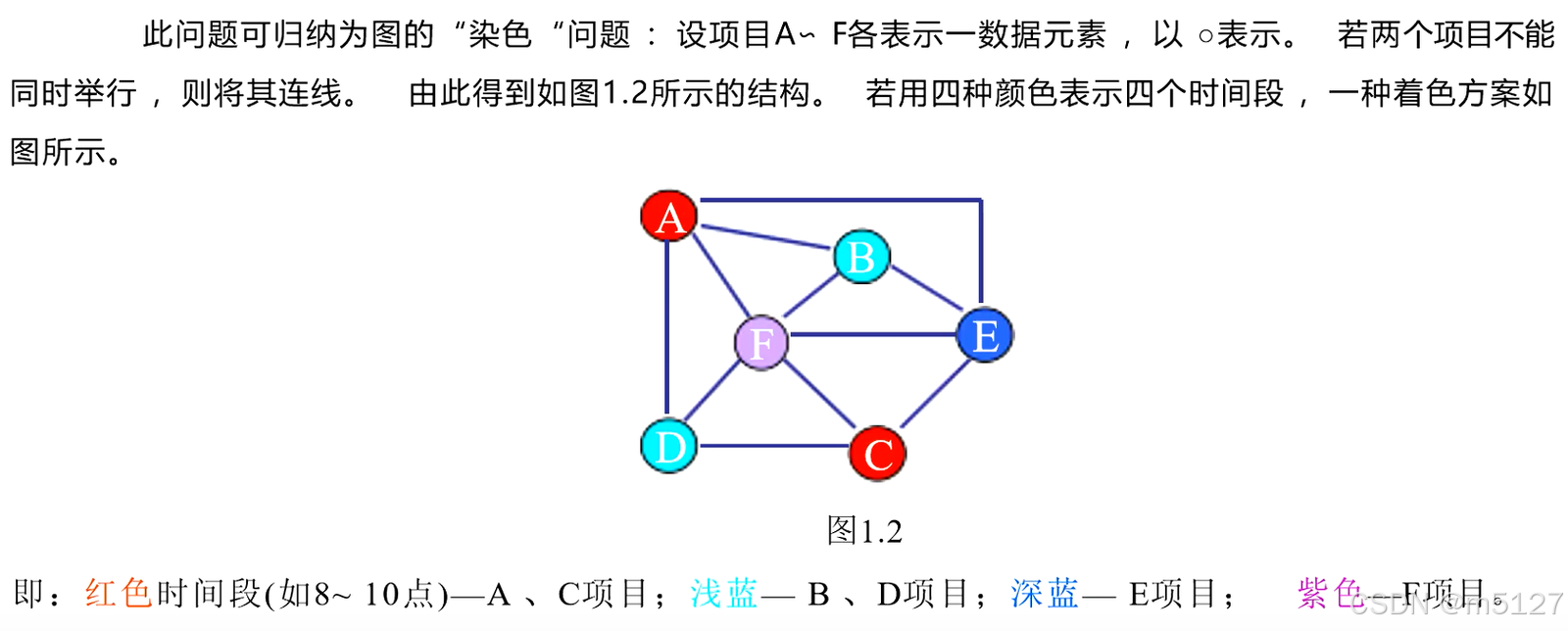
田径比赛的时间安排问题

1.3 存储结构

数据的逻辑结构在计算机中的具体实现

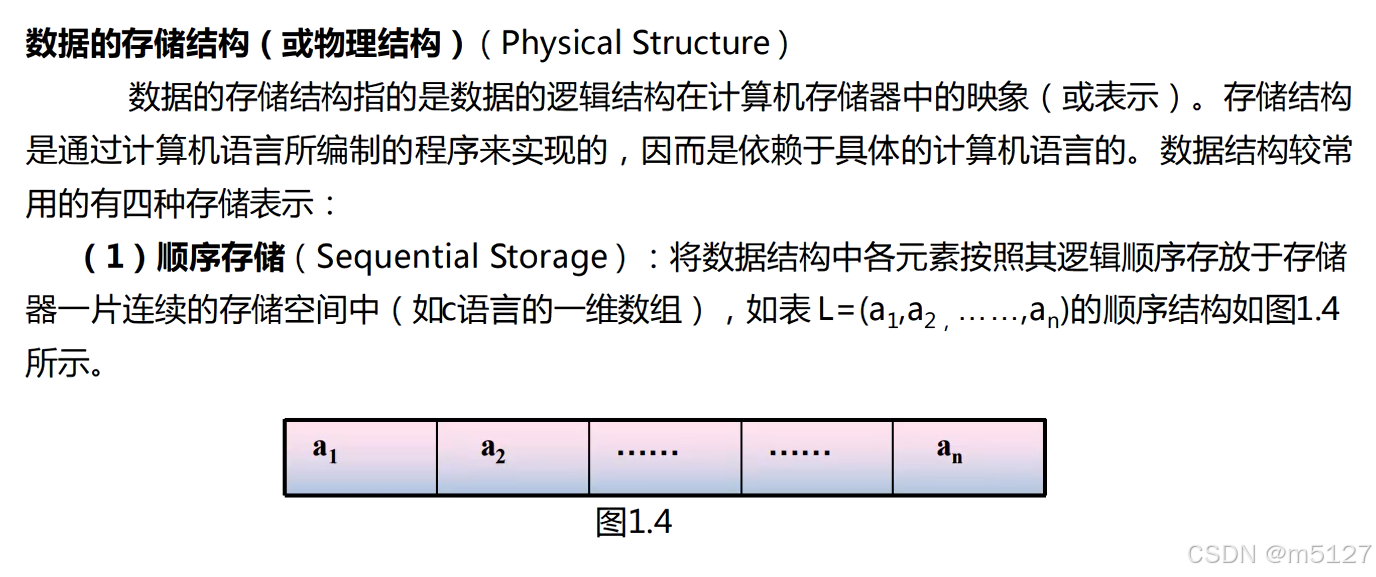
1.3.1 顺序存储

数组：连续存储

特点：内存连续、随机存取，每个元素占用空间较少

缺点：只能用一块大的且连续的空间，会产生一些碎片化的小空间

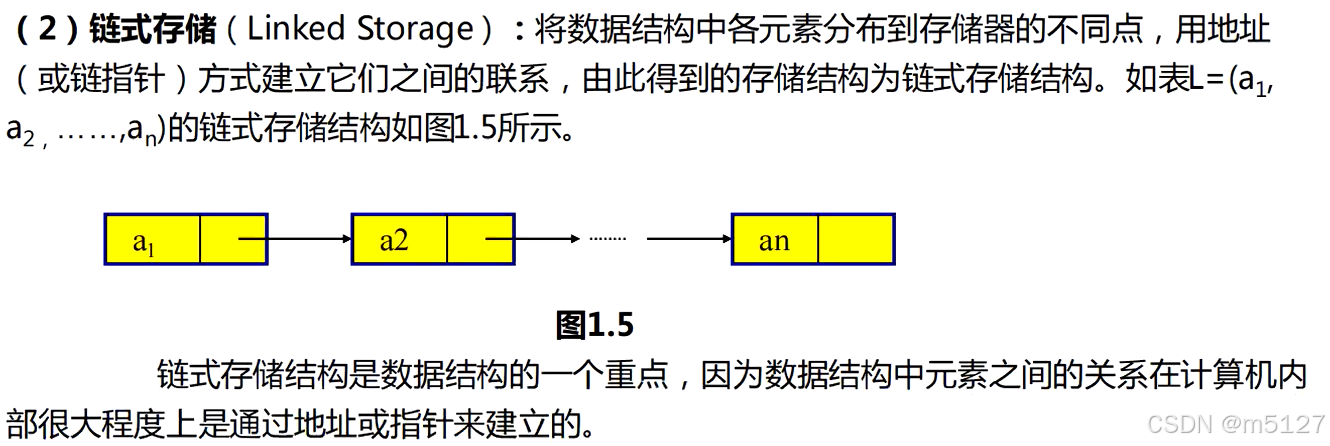
1.3.2 链式存储

通过指针存储

特点：内存不连续，通过指针实现

链表实现：

结构体：

#include <stdio.h>

struct node_t
{
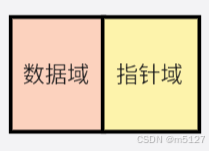
    int data;           // 数据域:存放节点的数据
    struct node_t *next;// 指针域：结构体指针指向下一个节点
};

int main(int argc, char const *argv[])
{
    struct node_t A = {1, NULL};
    struct node_t B = {2, NULL};
    struct node_t C = {3, NULL};

    A.next = &B;
    B.next = &C;
    return 0;
}

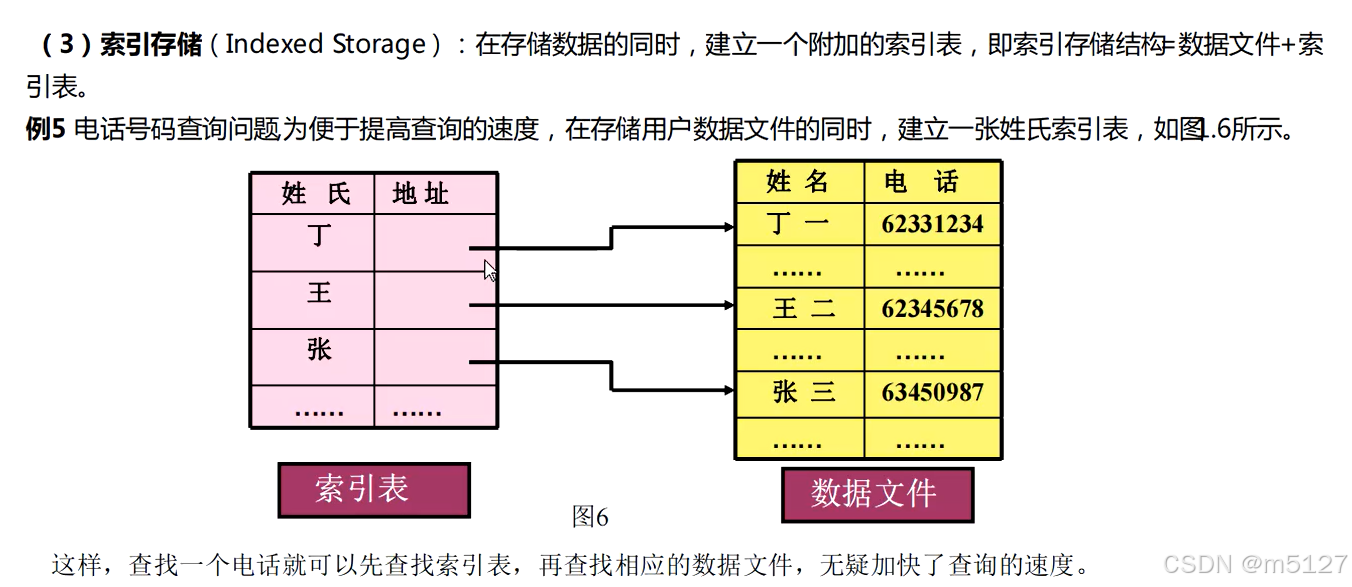
1.4.3 索引存储结构

在存储数据的同时，建立一个附加的索引表。

即索引存储结构=索引表+数据文件。

可以提高查找速度，特点检索速度快，但是占用内存多，删除数据文件要及时更改索引表。

例如：

这样查找一个电话就可以先查找索引表，再查找对应的数据文件，加快了查询的速度。但是如果删除或添加某个数据也要操作对应的索引表。

1.4.4 散列存储

数据存储按照和关键码之间的关系进行存取。关系由自己决定，比如关键码是key, 存储位置也就是关系是key+1。获取关键数据，通过元素的关键码方法的返回值来获取。

存的时候按关系存

取的时候按关系取

1.5 操作

增删改查

什么是算法

算法是解决问题的思想方法，数据结构是算法的基础。

2.1 算法的设计

算法的设计：取决于数据的逻辑结构

算法的实现：依赖于数据的存储结构

2.2 特性

有穷性：步骤是有限

确定性：每一个步骤有明确的含义，无二义性

可行性：规定的时间能完成

输入

输出

2.3 评价算法的好坏

正确性
易读性
健壮性：容错处理
高效性：执行效率，通过重复执行的次数来判断，也就是可以通过时间复杂度

时间复杂度：

语句频度：用时间规模函数表达

时间规模函数：T(n) = O(f(n))

T(n) // 时间规模函数的时间函数

O // 时间数量级

n // 问题规模例：a[100], n = 100

f(n) // 算法可执行语句重复执行次数

例子1：

求1+2+3+4+...+n的和

算法1：

int sum=0;

for(int i=1;i<=n;i++)

{

sum+=i;

}

// n = 100

f(n) = n;

T(n) = O(n);

算法2：

利用等差数列前n项和公式：Sn=n(a1+an)/2

int sum = n*(n+1)/2 // 当 n=100 重复执行一次

f(n) = 1;

O(f(n));

T(n) = O(1);

例2：

int i, j;
for(i = 0; i< n; i++)
{
    for(j = 0; j< n; j++)
    {
        printf("ok\n");
    }
}

// n*n 次

T(n) = O(n^2)

例3：

int i, j;
for(i = 0; i< n; i++)
{
    for(j = 0; j<=i; j++)
    {
        printf("ok\n");
    }
}

执行次数：1+2+3+..+n

f(n) = n*(n+1)/2;

= n^2/2+n/2; // 只保留最高项n^2/2，除以最高项系数得到n^2

T(n) = O(n^2)

计算大O的方法

根据问题规模n写出表达式f(n)
如果有常数项，将其置为1 //当f(n)的表达式中只有常数项的时候，例如f(n)=8 ==> O(1)
只保留最高项，其他项舍去。
如果最高项系数不为1，则除以最高项系数。

f(n) = 3*n^4 + 2*n^3 + 6*n^7 +10;

==> O(n^7)

线性表

线性表是最基本、最简单、也是最常用的一种数据结构，可以存储逻辑关系为线性的数据。线性表（linear list）是数据结构的一种，一个线性表是n个具有相同特性的数据元素的有限序列。

包含：顺序表（数组）、链表（单向链表、单向循环链表、双向链表、双向循环链表）、栈（顺序栈、链式栈）、队列(循环队列、链式队列)

逻辑结构：线性结构

存储结构：顺序存储(通过数组)或链式存储(通过指针)

特点：一对一，每个节点最多一个前驱和一个后继，首节点无前驱，尾节点无后继。

3.1 顺序表

顺序表存储数据的具体实现方案是：将数据全部存储到一整块内存空间中，数据元素之间按照次序挨个存放。

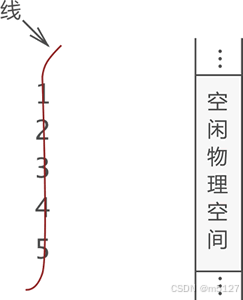
举个简单的例子，将 {1,2,3,4,5} 这些数据使用顺序表存储，数据最终的存储状态如下图所示：

3.1.1 顺序表的特性

特点：内存连续

逻辑结构：线性结构

存储结构：顺序存储

操作：增删改查

3.1.2 操作数组

例题：

int a[100] = {1, 2, 3, 4, 5, 6, 7, 8};

函数命令规则：

下划线法：create_empty_seqlist

小驼峰法：createEmptySeqList

大驼峰法：CreateEmptySeqList

插入数组元素

/*  
    功能：向数组的第几个位置插数据
    函数：void insetIntoA(int *p,int n, int post, int data);
    参数：
    int *p: 保存数组首地址
    int n: 有效数据元素的个数
    int post: 插入元素下标
    int data: 数据
*/
void insertIntoA(int *p, int n, int post, int data)
{
    // 1. 把从最后一个元素p[n-1]到插入位置元素 p[post]向后移动一个位置
    for(int i = n-1; i >= post; i--)
        p[i+1] = p[i];
    // 2. 插入新元素data到指定位置
    p[post] = data;
}

遍历数组中的有效元素

/*
    功能：遍历数组中的有效元素
    函数：void showA(int *p,int n);
    参数：
    int *p:保存数组收地址
    int n:有效数据元素的个数
*/
void showA(int *p,int n)
{
    for(int i = 0; i < n; i++)
        printf("%d ", p[i]);
    printf("\n");
}

删除数组元素

/*  功能：删除数组中指定元素 
    函数：void deleteIntoA(int *p,int n, int post);
    参数：
    int *p: 保存数组首地址
    int n: 有效数据元素的个数
    int post: 删除元素下标
*/
void deleteIntoA(int *p, int n, int post)
{
    // 从删除位置后一个元素 p[post+1]到最后一个元素 p[n-1]往前移动一个单位
    for(int i = post+1; i < n; i++)
        p[i-1] = p[i];
}

#include <stdio.h>

void insertIntoA(int *p, int n, int post, int data)
{
    // 1. 把从最后一个元素p[n-1]到插入位置元素 p[post]向后移动一个位置
    for(int i = n-1; i >= post; i--)
        p[i+1] = p[i];
    // 2. 插入新元素data到指定位置
    p[post] = data;
}
void showA(int *p,int n)
{
    for(int i = 0; i < n; i++)
        printf("%d ", p[i]);
    printf("\n");
}
void deleteIntoA(int *p, int n, int post)
{
    // 从删除位置后一个元素 p[post+1]到最后一个元素 p[n-1]往前移动一个单位
    for(int i = post+1; i < n; i++)
        p[i-1] = p[i];
}
int main(int argc, char const *argv[])
{
    int arr[100] = {1, 2, 3, 4, 5, 6, 7, 8};
    insertIntoA(arr, 8, 2, 100);
    showA(arr, 9);
    deleteIntoA(arr, 9, 3);
    showA(arr, 8);
    return 0;
}

添加全局变量last 表示有效元素下标

#include <stdio.h>

int last = 7;  // 代表最后一个有效元素的下标 last=有效元素个数-1

void insertIntoA(int *p, int post, int data)
{
    // 1. 把从最后一个元素p[n-1]到插入位置元素 p[post]向后移动一个位置
    for(int i = last; i >= post; i--)
        p[i+1] = p[i];
    // 2. 插入新元素data到指定位置
    p[post] = data;

    last++;
}
void showA(int *p)
{
    for(int i = 0; i <= last; i++)
        printf("%d ", p[i]);
    printf("\n");
}
void deleteIntoA(int *p, int post)
{
    // 从删除位置后一个元素 p[post+1]到最后一个元素 p[n-1]往前移动一个单位
    for(int i = post+1; i <=last; i++)
        p[i-1] = p[i];
    last--;
}

int main(int argc, char const *argv[])
{
    int arr[100] = {1, 2, 3, 4, 5, 6, 7, 8};
    insertIntoA(arr, 2, 100);
    showA(arr);
    deleteIntoA(arr, 3);
    showA(arr);
    return 0;
}

3.1.3 顺序表编程实现

seqlist.h

#ifndef __SEQLIST_H__
#define __SEQLIST_H__
#define N 10
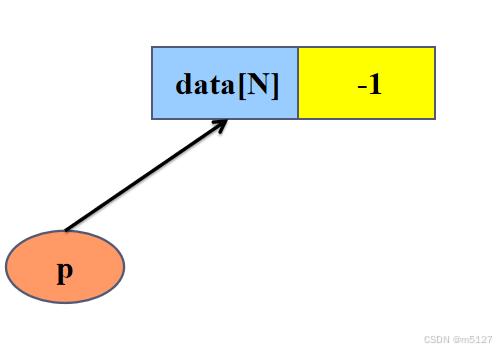
typedef struct seqlist
{
    int data[N];
    int last; //代表数组中最后一个有效元素的下标
} seqlist_t;

//1.创建一个空的顺序表
seqlist_t *CreateEpSeqlist();
//2.向顺序表的指定位置插入数据
int InsertIntoSeqlist(seqlist_t *p, int post, int data);
//3.遍历顺序表sequence顺序list表
void ShowSeqlist(seqlist_t *p);
//4.判断顺序表是否为满，满返回1,未满返回0
int IsFullSeqlist(seqlist_t *p);
//5.判断顺序表是否为空
int IsEpSeqlist(seqlist_t *p);
//6.删除顺序表中制定位置的数据
int DeleteIntoSeqlist(seqlist_t *p, int post);
//7.清空顺序表 (清空：访问不到，但是内存中还有；销毁：内存清空)
void ClearSeqList(seqlist_t *p);
//8.修改指定位置的数据，post为被修改数据位置，data为修改成的数据
int ChangePostSeqList(seqlist_t *p,int post,int data);
//9.查找制定数据出现位置,data为被查找的数据，返回下标，未找到返回-1
int SearchDataSeqList(seqlist_t *p,int data);
#endif