题目描述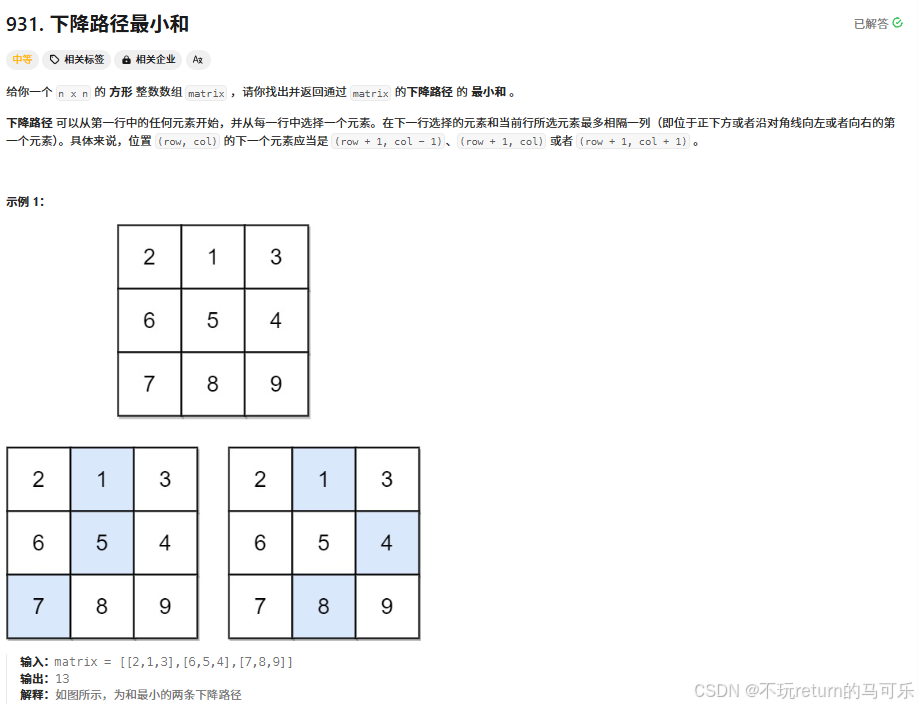
解题思路
这个问题可以通过动态规划来解决。我们定义一个二维数组 dp,其中 dp[i][j] 表示从第一行到第 i 行,且第 i 行选择第 j 列元素的最小路径和。我们可以从第一行开始,逐行计算 dp 数组的值。
算法步骤
-
初始化
dp数组的第一行与matrix的第一行相同,因为第一行的元素可以直接到达。 -
从第二行开始,对于每一行的每个元素
matrix[i][j],找到其上方、左上方和右上方的最小路径和,并加上当前元素的值,更新dp[i][j]。 -
在计算完
dp数组的最后一行后,找到其中的最小值,即为通过matrix的下降路径的最小和。
代码实现
class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n = matrix.size();
vector<vector<int>> dp(n, vector<int>(n));
// 初始化dp数组的第一行为matrix的第一行
for (int i = 0; i < n; i++) {
dp[0][i] = matrix[0][i];
}
// 从第二行开始计算dp数组
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
int minVal = INT_MAX;
// 找到当前位置上方、左上方和右上方的最小值
for (int k = -1; k <= 1; k++) {
int col = j + k;
if (col >= 0 && col < n) {
minVal = min(minVal, dp[i - 1][col]);
}
}
// 更新dp数组
dp[i][j] = matrix[i][j] + minVal;
}
}
// 找到dp数组的最后一行中的最小值
int minSum = INT_MAX;
for (int i = 0; i < n; i++) {
minSum = min(minSum, dp[n - 1][i]);
}
return minSum;
}
};复杂度分析
-
时间复杂度:O(n3),其中 n 是矩阵的行数(或列数)。我们需要三层循环来计算
dp数组的值。 -
空间复杂度:O(n2),用于存储
dp数组。
总结
这个问题是一个典型的动态规划问题,通过定义状态转移方程并逐行计算 dp 数组的值,我们可以找到通过矩阵的下降路径的最小和。这种方法不仅适用于这个问题,也可以推广到其他类似的路径问题中。