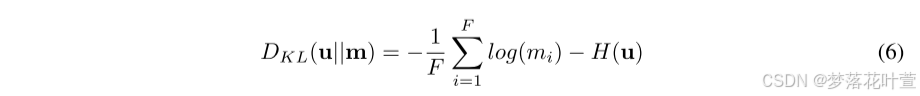Notice：此篇文章为论文精读。
Paper来源：点我跳转

Abstract

解决了表格数据（即结构化数据）中的异常检测问题——通常由one-class分类（只有一个类别或类别的样本集用于训练模型。通常，这个类别包含所谓的正常或良性样本，而异常样本或异常类别是未知的或未在训练数据中包含的）设置实现，训练集仅包含正常样本。

本文主要工作：扩展了遮罩建模方法，捕获训练集中特征之间的内在相关性，偏离这种相关性的样本极有可能是异常。

贡献1：如何获得多元和多样化的相关性——新遮罩策略（学习产生多个遮罩）

贡献2：设计多样性损失来减少不同遮罩的相似性（使用多样性损失，遮罩之间的相似性被最小化，这意味着生成的遮罩在某些标准或度量下彼此之间是不同的）。

贡献3：从每个独立特征的角度和特征之间的相关性去讨论这种方法的可解释性。

1 Introduction

• 举例说明结构化数据异常检测的应用场景——医疗疾病检测[2021]、金融欺诈检测[2021]、网络入侵检测[2021]【水字数】。（后面一句话，我的理解是获取标记的异常做处理本来就没有意义，因为异常检测的目标就是在一堆数据里找出与大量数据背道而驰的少量数据，这也是训练集中只有正常样本的原因——对应one-class classification）
• AD 的关键是提取训练数据（正常样本）的特征模式。从定义上讲，就是将那些与正常样本的特征模式存在较大偏差的数据定义为异常[2021]。
• 自监督学习方法可以通过创建欺诈任务去训练神经网络来学习训练数据中的特征模式。
  举例子，GOAD[2020]用了基于距离的欺诈任务，最小化训练样本到聚类中心的距离。NeuTral AD[2021]和 ICL[2022]只采用基于对比学习的损失函数去建模，：
• NeuTral AD 方法首先学习一组变换，然后调整这些变换后的样本的表示，使其与原始样本更接近，同时与其他变换的样本的表示更远。
• ICL将单个样本分割成多个对，每个对包含样本的一个连续特征子集（样本中连续的、相邻的特征）和一个剩余特征子集（不连续的特征），随后就增强同一对中两个特征子集之间的相互信息（相互信息是一种度量，用于量化两个随机变量之间的依赖性。ICL的目标是增加同一对中连续特征子集和剩余特征子集之间的依赖性。），与此同时减少不同对中特征子集之间的相互信息。
• 没有工作将遮罩图像/语言建模（MIM/MLM已经在SSL中被证实了有效性，MIM是2021年提出的概念，MLM是2018年提出的概念）应用于表格异常检测（好像我最近刚好有看到一篇，回去再翻一翻）
• 作者把自己提出的MCM和MIM、MLM放在同一个高度。通过训练MCM来捕获训练数据中存在的特征之间的内在相关性，并通过这种相关性对“特征模式”进行建模。对于被遮罩的建模任务，通过对未被遮罩的特征的学习， 用最佳mask来捕捉相关性对遮罩样本进行重建，最小化重建损失。一般来说这些mask是需要手动去寻找的，相应地，作者提出了一种可学习的掩码策略，通过nn去找到mask。
• 方法强调：设计一个mask（上文所说的遮罩）生成器[原始数据输入，多个mask矩阵输出]，用这些mask矩阵和原始输入进行元素乘积（此处与点积进行区分，点积/内积得到一个数值，是两个向量之间的一种运算，通常用于计算两个向量之间的相似度；元素乘积指对两个向量中对应的元素进行逐个相乘的操作，通常用于组合两个向量中的元素），以此生成多个遮罩数据，然后通过神经网络重建。通过设计一个多样性损失，防止产生冗余mask。

2 Related Work

2.1 经典的AD方法——维度诅咒、低精度

• 基于概率的方法：利用参数或非参数分布来拟合正态数据，然后根据数据出现在该分布中的概率检测异常。（参数化：固定参数的分布，假设数据遵循某个特定的分布，并通过数据来估计这些分布的参数，例如均值和方差；非参数化：直接从数据中估计分布）
  • kernel based density estimator[2014]：非参数化方法，它使用核函数来估计数据的概率密度函数。
  • gaussian mixture models[2009]：参数化方法，假设数据是由多个高斯分布混合而成的。这种方法可以用来捕捉数据中的多个模式，并且可以用于检测那些不属于这些模式的异常点。
  • empirical cumulative distribution[2022]：非参数化方法，直接基于样本数据来构建累积分布函数。这种方法通过比较数据点的经验累积分布与理论分布来检测异常。
• 基于距离的方法：根据测试点与其他实例的距离来评估测试点。
  • KNN[2000]：计算一个测试点与其最近的k个邻居之间的平均欧几里得距离，并将这个距离作为异常分数[指标]。距离大即异常。
  • LOF[2000]：局部离群因子。计算一个样本的局部可达性密度（相对概念，描述了一个点在其邻域中的密度）与其最近邻的局部可达性密度之比。如果一个点的局部可达性密度远低于其最近邻，就被认为是异常的。
• 基于分类的方法：仅通过访问正常类别的数据来直接学习一个决策边界。
  • OCSVM[2001]：通过实现输入数据与坐标原点之间的最大分离来生成决策边界。目标是找到一个超平面（在多维空间中），使得所有正常数据尽可能远离这个超平面，并且超平面与原点之间的间隔最大。这样，任何位于超平面一侧的数据点都被认为是正常的，而位于另一侧的数据点则可能是异常。
  • Tax&Duin[2004]：试图学习一个能包围大多数样本的最小超球面，超球面的中心和半径是通过优化过程确定的。

2.2 AD中的自监督学习——解决维度诅咒——没TAD

• 训练分类器[2018/2019]：区分应用于给定图像的不同几何变换[旋转、缩放、翻转]。测试时使用分类器在变换后的图像上预测的softmax激活来检测异常。
• 随机仿射变换[2020]：[平移、旋转、缩放和剪切]将基于变换的方法应用于表格数据。
• 对比学习[2020]：通过拉近正样本对之间的距离并推开负样本对之间的距离来学习有效的数据表示。后续改进[2020]在训练时引入了一个额外的分类器，并将表示和分类器的信息结合起来进行预测。
• 马氏距离[2021]：考虑变量间相关性的距离度量。
• 一类分类器[2021]：前面讲过了，不说了。
• 对比学习的推广[2021]：设计可学习的变换和一个新颖的确定性对比损失来实现。
• 内部对比损失[2022]：一次考虑一个样本，并将其特征的一个子集与剩余特征匹配。关注于单个样本内部的特征之间的关系，而不是不同样本之间的关系。

2.3 遮罩图像/语言建模——严重依赖于L和I的内在结构

• BERT[2018]和GPT[2020]：Bidirectional Encoder Representations from Transformers-预训练语言表示的方法；Generative Pre-trained Transformer-基于Transformer的预训练语言模型。使用了掩码语言建模（MLM）目标[一种预训练任务，通过遮蔽输入文本中的某些单词并让模型预测它们来训练模型]
• BEiT[2021]：将MLM的成功扩展到CV领域，将原始图像分割成离散的token，然后通过BERT风格的预训练来学习表示。
• 感知损失[2023]：强制token具有丰富的感知信息。
• MAGE[2023]：可变的遮蔽比率来统一图像生成和表示学习。
• MAE[2022]：区别于BEiT，试图预测被遮蔽的像素而不是离散的token。
• SimMIM[2022]：用一个单层预测头简化了解码器。
• CAE[2023]：使用一个潜在回归器来分离表示学习和预训练任务完成的角色

3 Method

3.1 概览

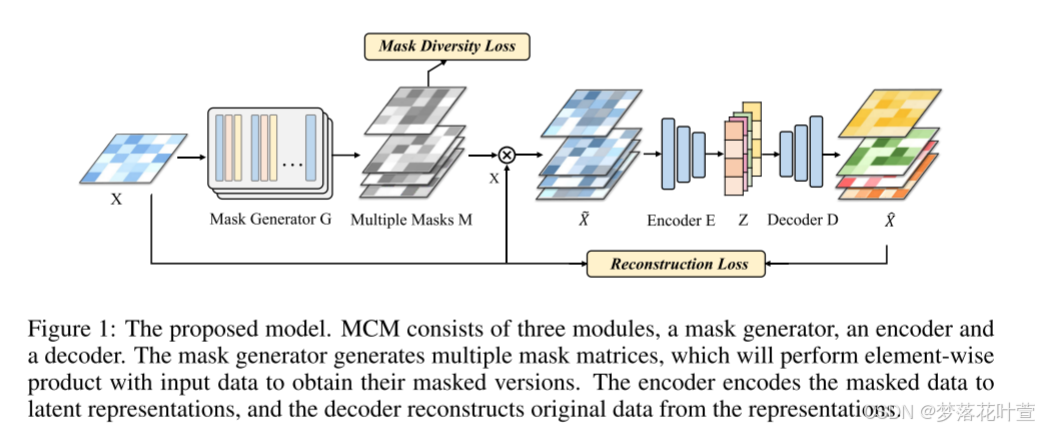
模型图如下，其实很好理解，一眼就能看明白：

跟着图走，第一步，Mask Generator G将样本X作为输入，Mask Generator G的输出为多个遮罩矩阵，即Multiple Masks M（对Multiple Masks M计算损失，使用Mask Diversity Loss旨在减少Multiple Masks M的冗余）。

第二步，将之前输入的样本X和每个遮罩矩阵执行元素乘积，产生的多个遮罩输入$\tilde{X}$。

第三步，再将这些$\tilde{X}$用Encoder E和Decoder E去编解码得到$\hat{X}$，计算重构损失Reconstruction Loss。

约束：Mask Diversity Loss+Reconstruction Loss

评估：测试样本的重构误差

3.2 遮罩策略

Mask Generator G组成：特征提取器F后接一个sigmoid函数

原理：G从X中学习信息，并输出一个与X同维度的遮罩矩阵M，sigmoid函数使得M中的每个值都在0到1的范围内[作者给出的理由是这提供了比传统的0或1的二值遮罩更灵活的遮罩程度]。

细节：遮罩矩阵M同时考虑了样本和特征两个维度——每一行是对X在不同特征上的遮罩，每一列是对一个特征在不同训练数据上的遮罩。

3.3 遮罩多样性

一个遮罩建模的相关性不足以区分正常数据和其他数据——那就多个，怎么做——集成学习，将多个特征提取器F1、F2、…、FK组装到遮罩生成器中，得到多个M。

$$M_1,M_2,...,M_K=G(X)=sigmoid(F_1(X),F_2(X),...,F_K(X))(1)$$

$${\tilde{X}}_k=X\odot M_k,{\hat{X}}_k=D(E({\tilde{X}}_k)),k=1,2,...,K.(2)$$

产生问题：如何防止遮罩生成器产生相同和冗余的遮罩？很重要，关乎MCM能否提取多样相关性。

解决方法：神经网络学习约束——计算所有矩阵之间的相似性之和，加到损失函数里。

进一步解读：

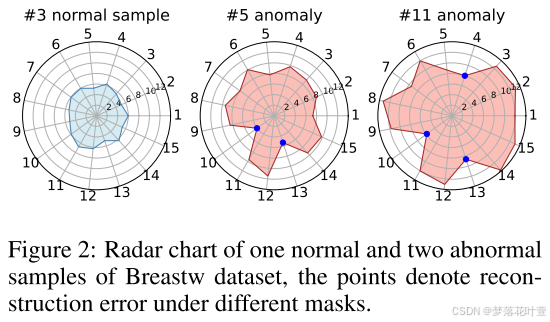
在某些情况下，特定的遮罩可能会与异常样本表现出一定的相关性。从图2例子来看，对于5和11号异常样本，只考虑使用第10或第13个遮罩时，重建误差较低。意味着在一个特定的视角或特征集下，异常样本与正常样本的分布相似，可能是因为这个异常样本恰好符合正常样本中的一些特征相关性。但是，当考虑多种不同的特征相关性时，异常样本就很难在所有方面都与正常样本保持一致了。我们可以看图2中多个遮罩组成的异常样本的重建误差较大，表明它们在这些特征下与正常样本不匹配。

3.4 损失表示

$$\mathcal{L}={\mathcal{L}}_{rec}+\lambda {\mathcal{L}}_{div}(3)$$

$${\mathcal{L}}_{rec}=\frac{1}{K}\sum _{k=1}^K||{\hat{X}}_k-X|{|}_F^2=\frac{1}{NK}\sum _{i=1}^N\sum _{k=1}^N||{\hat{\mathbf{x}}}_k^{(i)}-{\mathbf{x}}^{(i)}|{|}_2^2(4)$$

$${\mathcal{L}}_{div}=\sum _{i=1}^K\left[\mathsf{ln}(\sum _{j=1}^K(e^{<M_i,M_j>/\tau }\cdot 1_{i\ne j}))\cdot scale\right](5)$$

参数解读：

公式（3）：${\mathcal{L}}_{rec}$——重构损失；${\mathcal{L}}_{div}$——多样性损失；$\lambda$ ——超参数

公式（4）：${}^{(i)}$——样本索引；${}_k$——不同遮罩的索引；$N$——训练数据总数；$K$——遮罩总数

${\mathcal{L}}_{rec}=\frac{1}{K}{\sum }_{k=1}^K||{\hat{X}}_k-X|{|}_F^2$：这部分表示对于每个遮罩k（总共有K个遮罩），计算重构数据${\hat{X}}_k$和原始未遮罩数据X之间的差异，并求这些差异的L2范数。然后，将所有遮罩的重构损失求和，并除以遮罩的总数来计算平均重构损失。

$\frac{1}{NK}{\sum }_{i=1}^N{\sum }_{k=1}^N||{\hat{\mathbf{x}}}_k^{(i)}-{\mathbf{x}}^{(i)}|{|}_2^2$：这部分是对第一部分的进一步细化。这里，${\hat{\mathbf{x}}}_k^{(i)}$表示第 i个样本在第 k个遮罩下的重构数据，${\mathbf{x}}^{(i)}$表示第i个样本的原始未遮罩数据。对于每个样本i（总共有N个训练样本）和每个遮罩k，计算重构数据与原始数据之间的差异的平方欧几里得范数。这个双求和操作首先对所有样本和遮罩的组合计算重构损失，然后通过除以NK（样本数和掩码数的乘积）来计算平均重构损失。
公式（5）：
${\sum }_{i=1}^K$：对K个不同的遮罩矩阵$M_i$进行求和

$<M_i,M_j>$：表示遮罩矩阵$M_i$和$M_j$之间的内积操作（衡量两个矩阵的相似性）。

$e^{<M_i,M_j>/\tau }$：$\tau$ 是温度参数[temperature]，用于调节相似性度量的敏感度。较高的 $\tau$ 值会减少相似性的影响，而较低的 $\tau$ 值会增强相似性的影响。

$1_{i\ne j}$：确保在计算相似性时排除遮罩矩阵与其自身的内积，只考虑不同遮罩矩阵之间的相似性。

$\mathsf{ln}$：将指数函数的结果转换为一个更易于优化的形式
${\sum }_{j=1}^K(e^{<M_i,M_j>/\tau }\cdot 1_{i\ne j})$：表示对K个遮罩矩阵中所有与$M_i$不相同的遮罩矩阵的相似性进行求和。

$scale$：一个缩放因子，文中给出$scale=1/|Mln1/M|$，（我这里看不懂，得去看代码定义）用于调整多样性损失的数值范围。这里的M是遮罩矩阵的总数，ln是自然对数。这个缩放因子的目的是使多样性损失在数值上与其他损失（如重构损失）保持一致，便于在优化过程中平衡它们的重要性。简单来说就是超参数了。

4 Experiments

4.0 实验准备

4.0.1 数据集

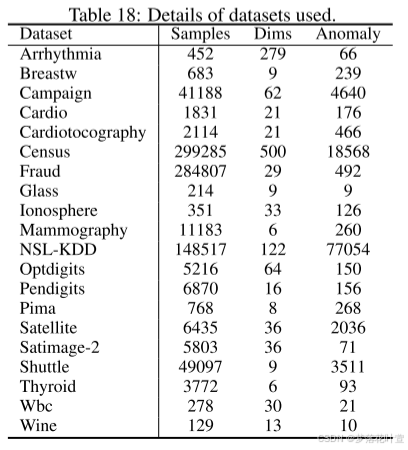
20个AD中常用的表格数据集，包括医疗保健、金融、社会科学等领域。12个来自ODDS[2016]，8个来自ADBench[2022]，可以简单看下Appendix E的表18：包括显示样本的数量、维度和使用的每个数据集的异常数。

4.0.2 评估指标

将每个数据集的正常数据随机分成两半。训练集由一半的正常数据组成，而测试数据集由另一半的正常数据和所有异常实例组成。

采用Area Under the Receiver Operating Characteristic Curve（AUC-ROC）和Area Under the Precision-Recall Curve（AUC-PR）作为评估标准。

AUC-ROC：ROC曲线是一个图表，显示了分类模型在不同阈值下的真正率（True Positive Rate, TPR）和假正率（False Positive Rate, FPR）之间的关系。AUC-ROC值是ROC曲线下的面积，其值范围从0到1。一个完美的分类器会有一个AUC-ROC值为1，而一个随机猜测的分类器则接近0.5。AUC-ROC是评估分类模型性能的常用指标，尤其是在类别不平衡的情况下。
AUC-PR：Precision-Recall曲线是一个图表，显示了分类模型在不同阈值下的精确率（Precision）和召回率（Recall）之间的关系。AUC-PR值是Precision-Recall曲线下的面积，其值范围同样从0到1。在类别不平衡的情况下，特别是异常检测任务中，AUC-PR通常比AUC-ROC更为重要，因为它更关注少数类（异常类）的性能。

4.0.3 具体细节

Mask Generator G组成：一组MLP后接sigmoid

E/D：对称，三层MLP后接LeakyReLU

超参数不敏感——多个数据集共用超参数

epochs：200

batch size：512

遮罩矩阵数量：15

$\tau$：0.1

隐藏层特征数：256

ED中间的低维度特征数：128

学习率和权重$\lambda$：针对不同数据集调整的唯一两个参数。权重$\lambda$作用为平衡两部分损失。

Adam optimizer：以指数衰减学习率控制器为界。

4.0.4 基线模型

包括IForest、LOF、OCSVM、ECOD和DeepSVDD在内的五种方法的实现都来自pyod[2019]库——一个集成了各种AD方法的综合Python库。其他四种方法的实现基于它们的官方开源代码版本。所有方法都使用相同的数据集分区和预处理过程来实现，参考最新工作[2021][2022]。每个实验运行三次，文章给出平均结果。

[1]:Yue Zhao, Zain Nasrullah, and Zheng Li. Pyod: A python toolbox for scalable outlier detection. arXiv preprint arXiv:1901.01588, 2019.

[2]:Chen Qiu, Timo Pfrommer, Marius Kloft, Stephan Mandt, and Maja Rudolph. Neural transformation learning for deep anomaly detection beyond images. In International Conference on Machine Learning, pp. 8703–8714. PMLR, 2021.

[3]:Tom Shenkar and Lior Wolf. Anomaly detection for tabular data with internal contrastive learning. In International Conference on Learning Representations, 2022.

4.1 主要结果

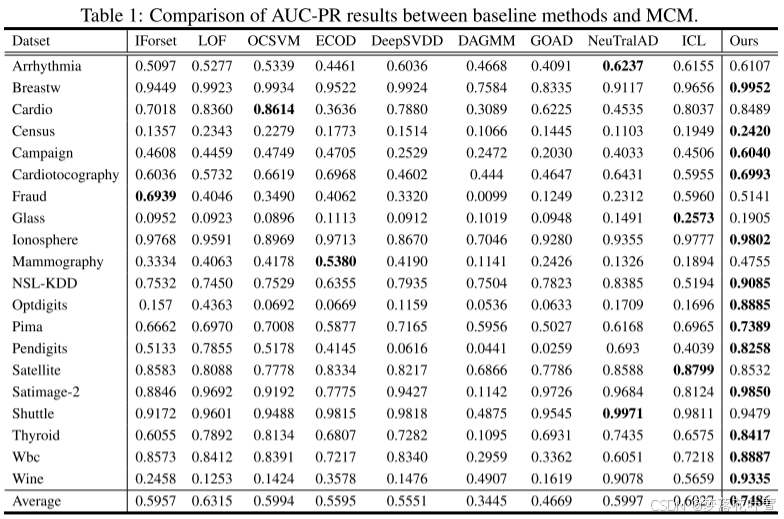
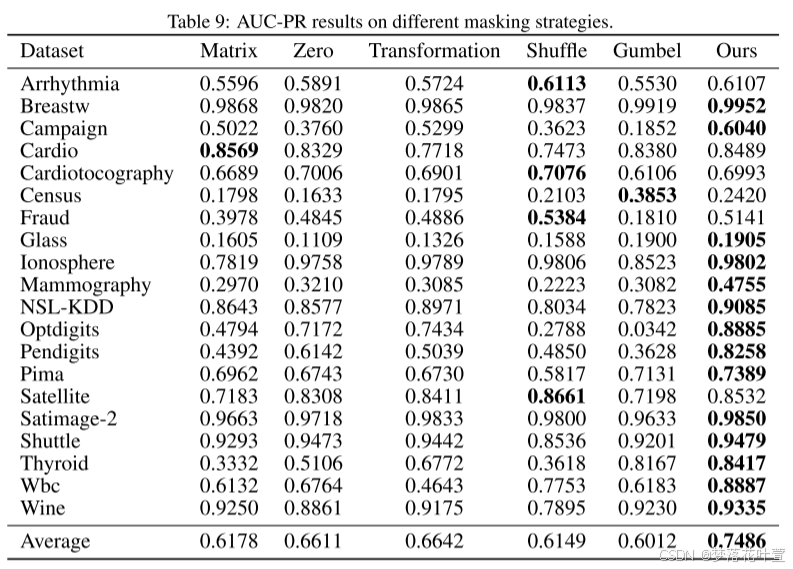
表1中展示了AUC-PR结果，AUC-ROC性能可以在附录A的表5中找到

MCM在20个数据集中的13个数据集上实现了最佳性能。即使在略低于最佳性能方法的数据集上，MCM性能差距仍然保持在可接受的范围内。

4.2 消融分析

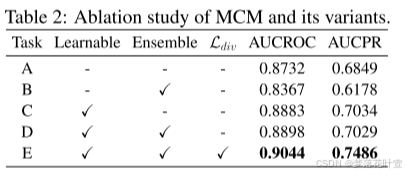
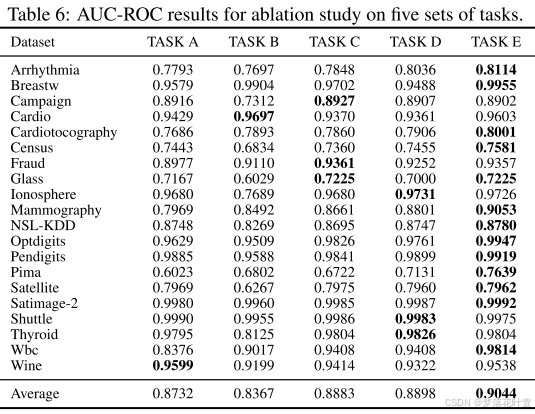
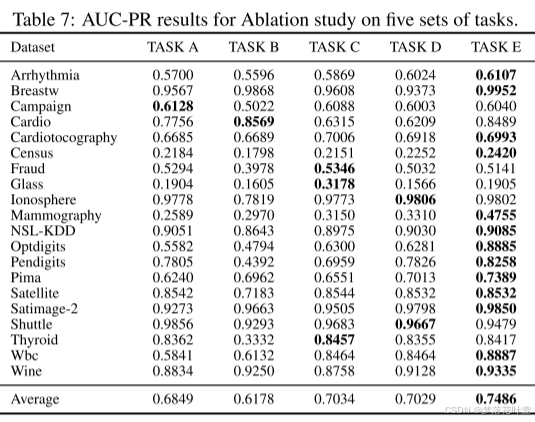
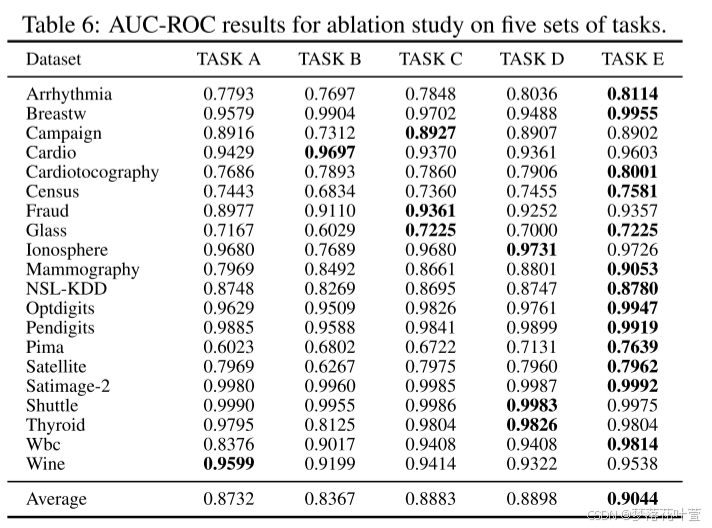
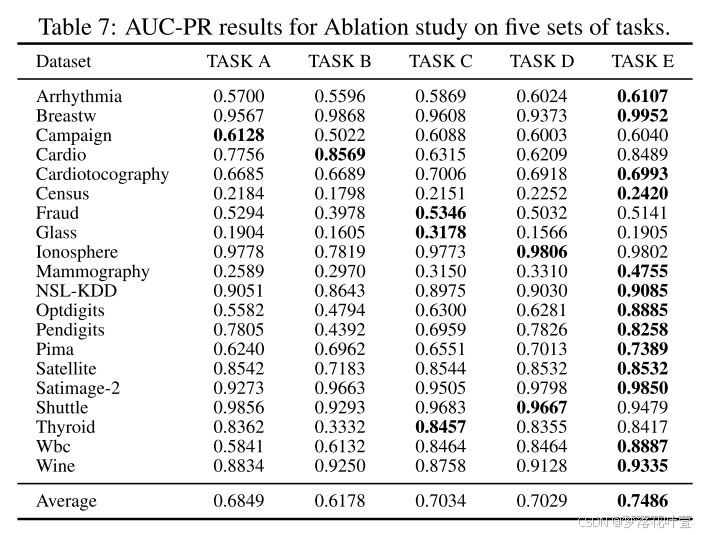
计算了上述数据集的AUC-ROC和AUC-PR，表2中显示了平均结果。每个数据集的详细结果在附录B的表6和表7中提供。

• Task A：普通AE，没有任何遮罩。
• Task B：随机采样的遮罩矩阵代替可学习遮罩矩阵，结果甚至不如没有遮罩操作的AE。
• Task C：不使用集成学习方法，将遮罩数量设置为一个[此时${\mathcal{L}}_{div}$不适用]。
• Task D：使用集成学习，不计算${\mathcal{L}}_{div}$。
• Task E：本文的方法。

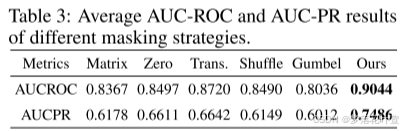
4.3 不同的遮罩策略

很霸道：作为将MIM/MLM成功扩展到表格AD的第一项工作，作者系统地研究了不同的遮罩策略。

• Matrix Masking：生成一个矩阵M，其值从均匀分布中随机抽取，然后通过使用M执行元素乘积来屏蔽所有输入。
• Zero Masking：以概率$p_m$随机采样一些特征，并用零值遮罩它们。
• Transformation Masking：生成一个矩阵W，其值从正态分布中随机抽取，然后使用输入样本和W执行矩阵乘法[2020]。
• Shuffle Masking：用概率$p_m$随机采样一些特征，并用从该特征的经验边际分布中随机抽取的样本去遮罩它们[2022]。
• Gumbel Masking：在遮罩生成器G中采用Gumbel-Softmax[2017]而不是sigmoid函数去生成可学习的二进制掩码。

Zero和Shuffle里的$p_m$设置为0.4。对于Zero和Shuffle，随机性反映在要遮罩的特征的选择上；Matrix和Transformation的随机性是通过矩阵M和W的生成引入的。

这些随机策略使表格AD很容易产生无意义的遮罩。

本文遮罩是基于数据生成的，没有引入随机性，可以捕捉正常数据中的特征相关性。本文的遮罩策略可看3.2。

4.4 不同类型的异常

异常的类型是列举不完的，但根据一篇文章[2022]总结，可以分成四种，并提出了生成它们的方法：

• Local anomalies
• Global anomalies
• Dependency anomalies
• Clustered anomalies

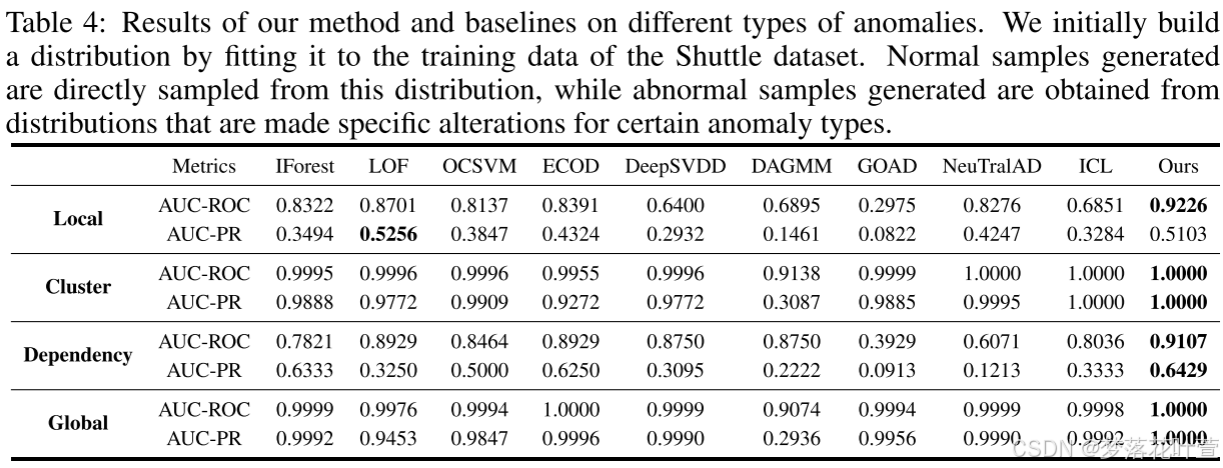
作者遵循相同的设置进行实验，用基于现实的航天飞机数据集生成人造异常，并评估MCM对特定类型异常的性能。附录C中描述了四种异常的生成过程，以下列出

• Local anomalies：使用经典的GMM程序（Milligan，1985；Steinbuss&Béohm，2021），生成正常样本。然后，通过缩放参数α=5缩放协方差矩阵来生成局部异常。
• Global anomalies：均匀分布$Unif(\alpha \cdot min(X^k),\alpha \cdot max(X^k))$，$\alpha$设置为1.1，用于控制异常偏差程度。
• Dependency anomalies：应用Vine Copula（Aas et al.，2009）方法对正常数据的依赖结构进行建模，通过去除建模后的依赖设置生成异常的概率密度函数，完成了独立性（参见（Martinez-Guela&Mata-Machuca，2016））。具体来说，使用核密度估计（KDE）（Hastie et al.，2009）来估计特征的概率密度函数并生成正常样本。
• Clustered anomalies：将正常样本的平均特征向量缩放为$\alpha =5$，即$\hat{\mu }=\alpha \hat{\mu }$。超参数$\alpha$控制异常簇与正常簇之间的距离。缩放GMM用于生成异常。

Dependency anomalies中：MCM可以提取正常数据中的相关性，从而熟练地检测特征之间缺乏相关性的异常。

4.5 进一步分析

4.5.1 Robustness to Anomaly Contamination

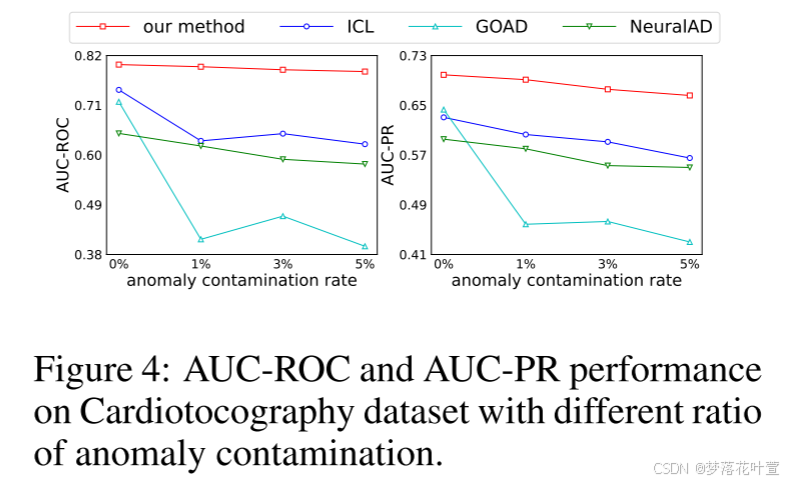
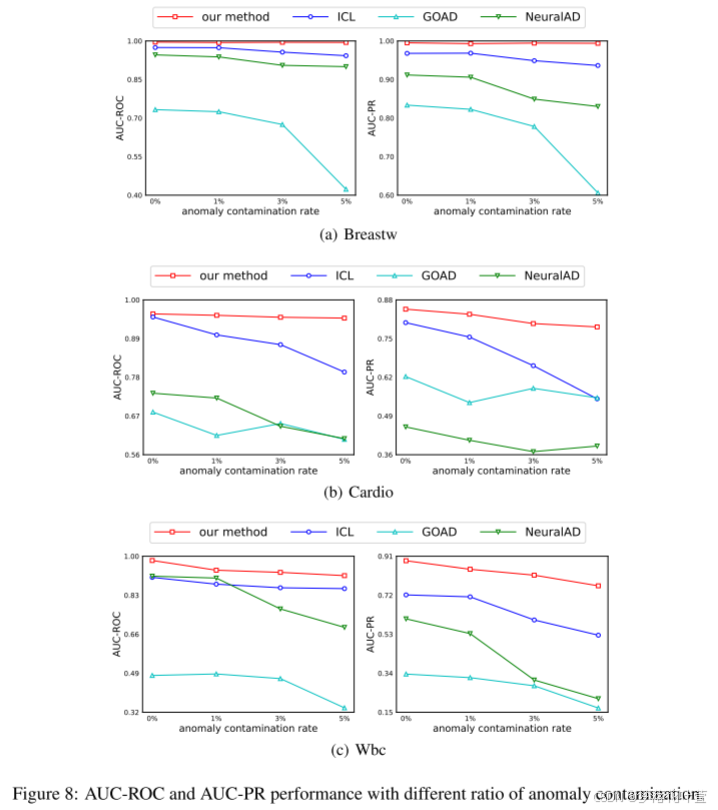
为了分析MCM w. r.t异常污染的鲁棒性，作者在异常污染率为0%、1%、3%和5%的情况下进行实验。随着污染率的增加，所有方法都遭受性能下降。但与其他三种基于SSL的方法相比，MCM执行更稳定，并且始终如一地显示出最佳性能，展示了MCM对异常污染的卓越鲁棒性。图4展示Cardiotocography dataset的结果，附录D展示了其他数据集的结果。

附录D：
（1）表16显示了一批不同维度数据的训练和推理时间，其中使用的生成数据范围从10到10,000个维度，批大小固定为64。 实验是在单个Tesla V100 GPU上进行的。

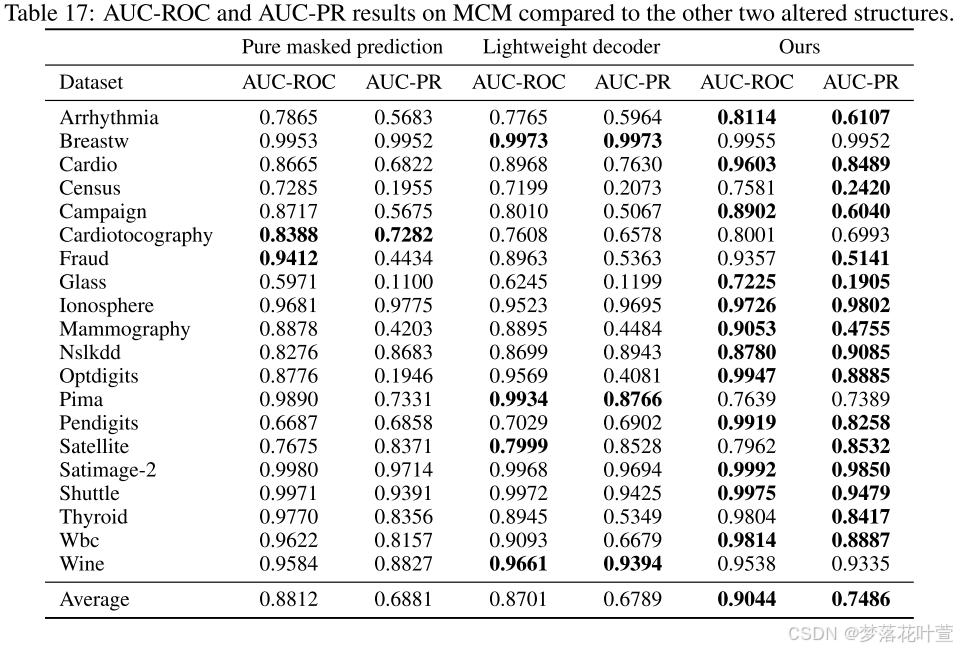
（2）在CV领域，已经证明使用轻量级解码器可以提高MIM的性能。 所以作者还尝试在这方面改变MCM，用one-layer head替换解码器，表17给出了MCM和改变结构的详细结果。这一变化对大多数数据集产生了负面影响，导致平均AUC-ROC和AUC-PR下降。造成这种差异的原因是:对于图像任务，编码器提取高级语义信息，使得重构像素等低级信息变得容易，并且使用轻量级解码器不会影响性能。然而，在表格数据中，单元格通常包含各种类型的信息，重建这些细粒度的表格数据，需要更强大的解码器来保证重建能力。

（3）Pure Masked Prediction，经典方法通常只计算masked part的重构误差，即pure masked prediction。 按照同样的设置，我们给每个特征的重构误差赋一个权重$1-m_j^i$，其中$m_j^i$是一个从0到1的值，表示第$i$个样本的第$j$个特征的遮罩程度。表17中的结果表明，这种变化也会导致较差的性能。

解释：unmasked part实际上是重建任务，而masked part是预测任务。在像MAE这样为图像设计的方法中，重建相对简单，添加它甚至会影响性能。 只关注预测部分确实可以迫使模型变得更强。 然而，表格数据具有更复杂的结构:列、行和单个单元格之间可能存在关系，并且还需要学习每个单元格中的语义。 因此，由于这些相互依赖关系，即使重建未被掩盖的部分也是具有挑战性的。 因此，通过捕获这些关系来改善未被掩盖部分的重建也是至关重要的，并且可以提高模型的性能。

4.5.2 The Number of Masking Matrices

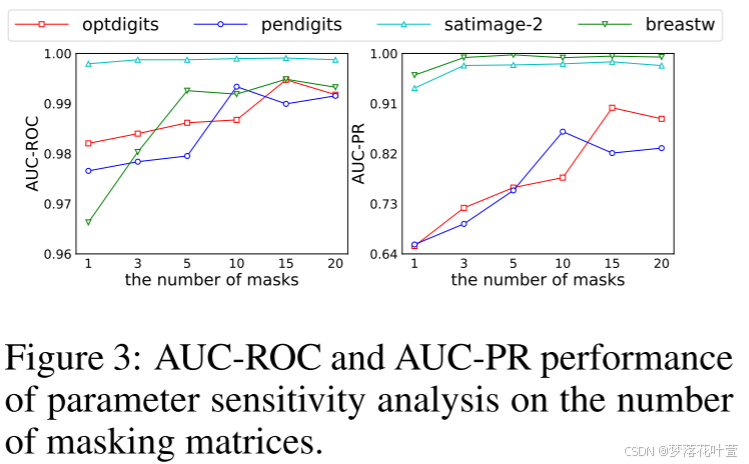
图3显示了不同遮罩矩阵数量下MCM的性能。一开始，随着遮罩矩阵数量的增加，四种数据集上的性能都有明显的提高。 因为更多样化的遮罩矩阵可以提取更多的正常数据的特征相关性，为判断异常提供更多的判别证据。 当遮罩矩阵的数量达到一个相对较高的值时，性能变得稳定。 在MCM中，作者将此参数固定为15，并且不针对不同的数据集进行调整。 其他超参数的灵敏度实验见附录B

附录B：消融和参数灵敏度

• 表6和表7，给出了消融研究在所有选定数据集上的详细AUC-ROC和AUC-PR表现。

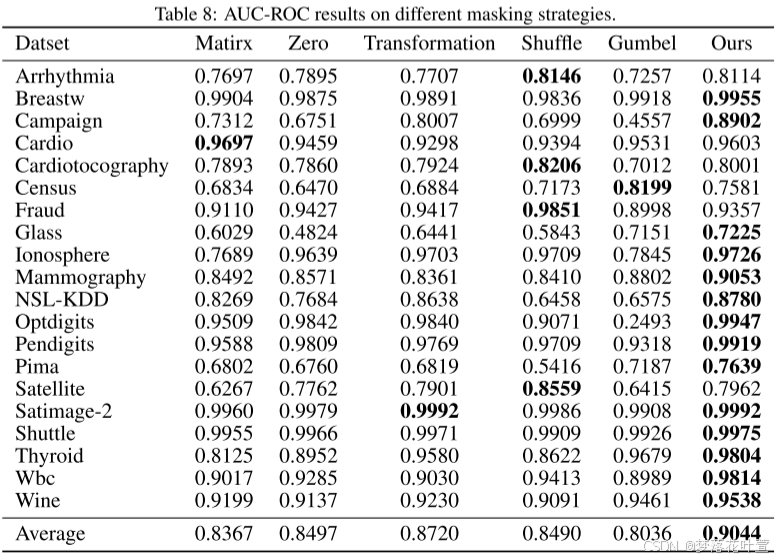
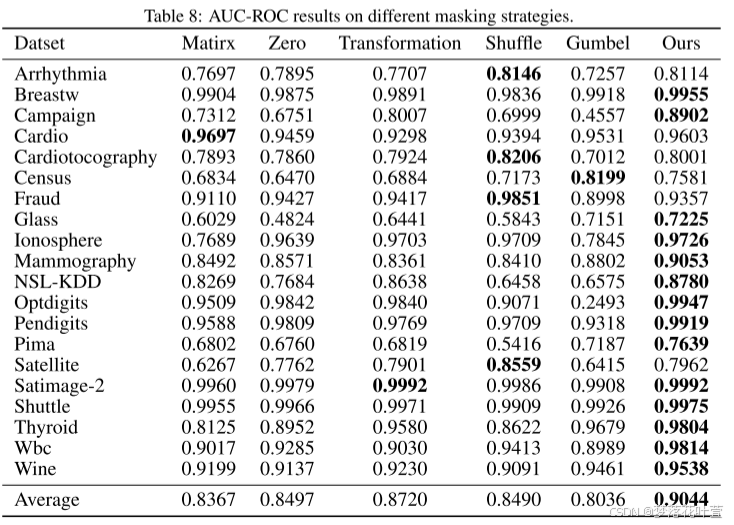
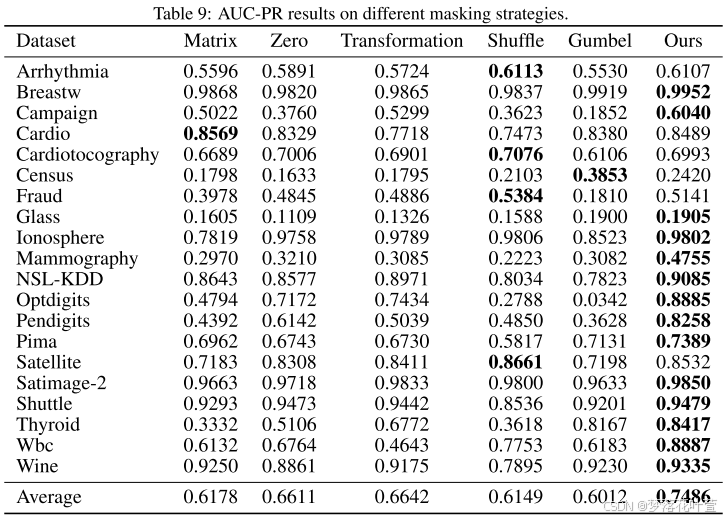
• 表8和表9显示了不同遮罩策略下的AUC-ROC和AUC-PR结果

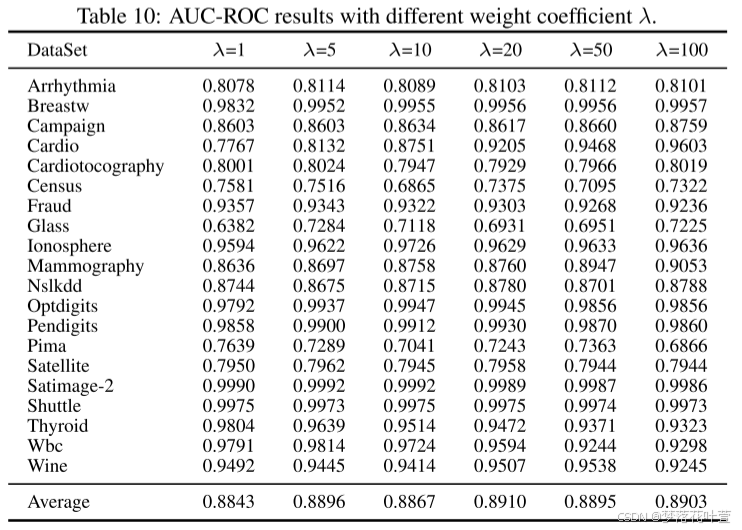
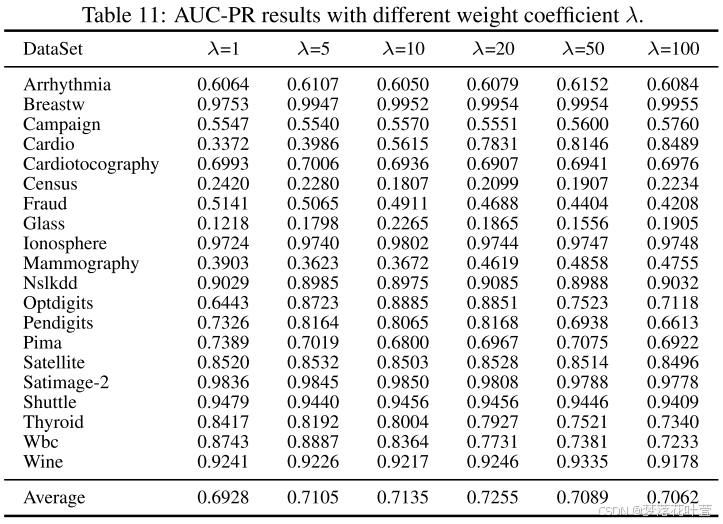
• 表10和表11给出了不同权重系数$\lambda$下的AUC-ROC和AUC-PR结果。 在之前的实验中，作者为每个数据集微调了$\lambda$。 在这里，为了探索对$\lambda$的敏感性，作者在所有数据集上使用固定的$\lambda$值进行了实验。 结果表明，$\lambda =20$时的性能最佳。 更重要的是，与每个数据集单独调整$\lambda$相比，平均AUC-PR仅下降0.0231，仍然超过所有基线方法，证明作者的方法对$\lambda$不敏感。

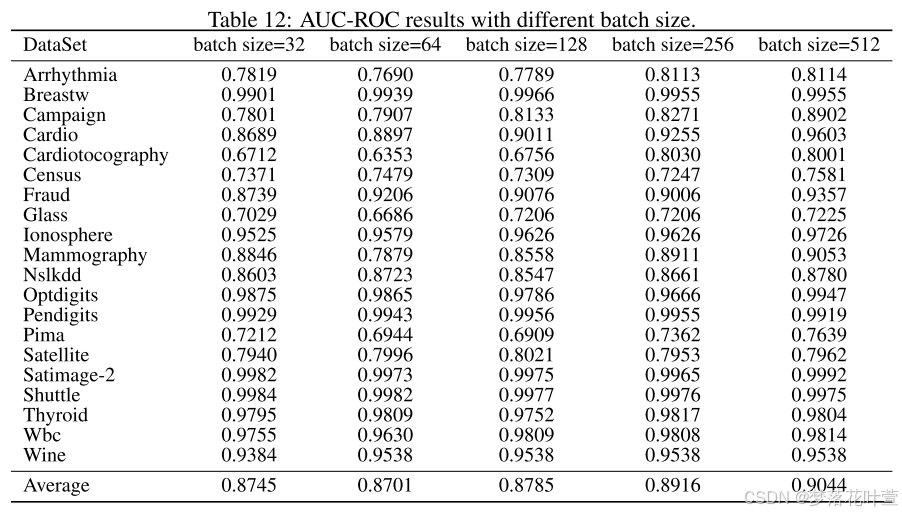
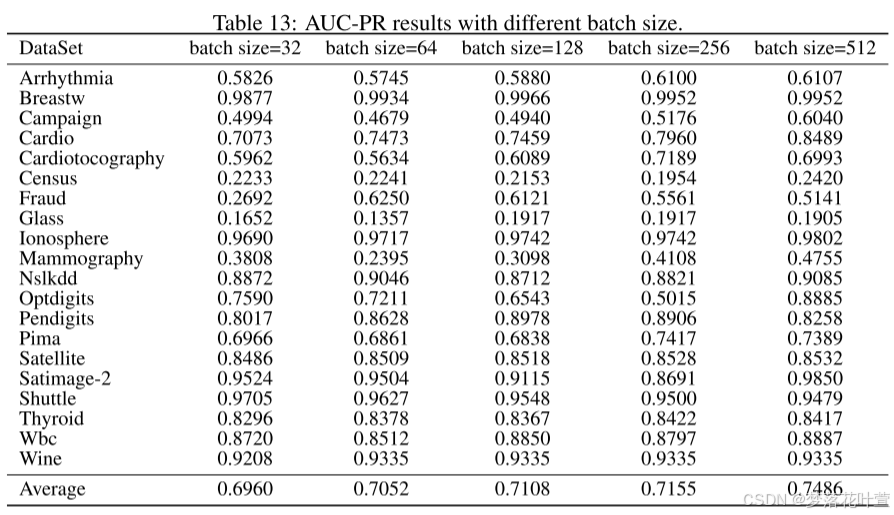
• 表12和表13显示了不同批量大小的AUC-ROC和AUC-PR结果。

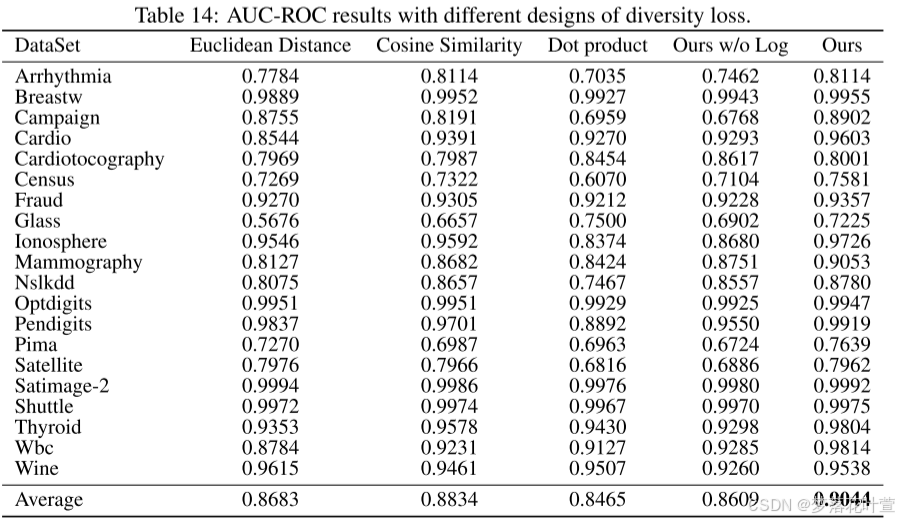
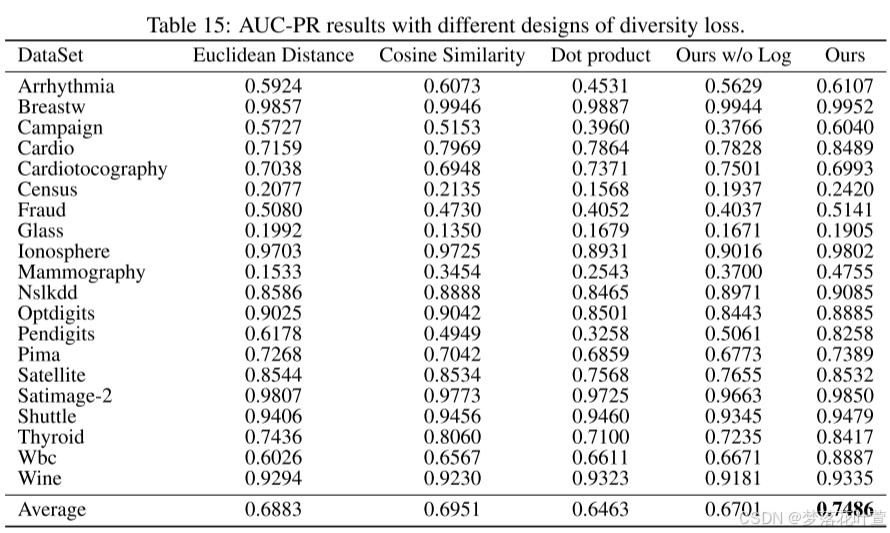
• 表14和表15显示了不同多样性损失设计下的AUC-ROC和AUC-PR结果。 在同一数据集上运行和测试时，确保权重系数$\lambda$保持不变。

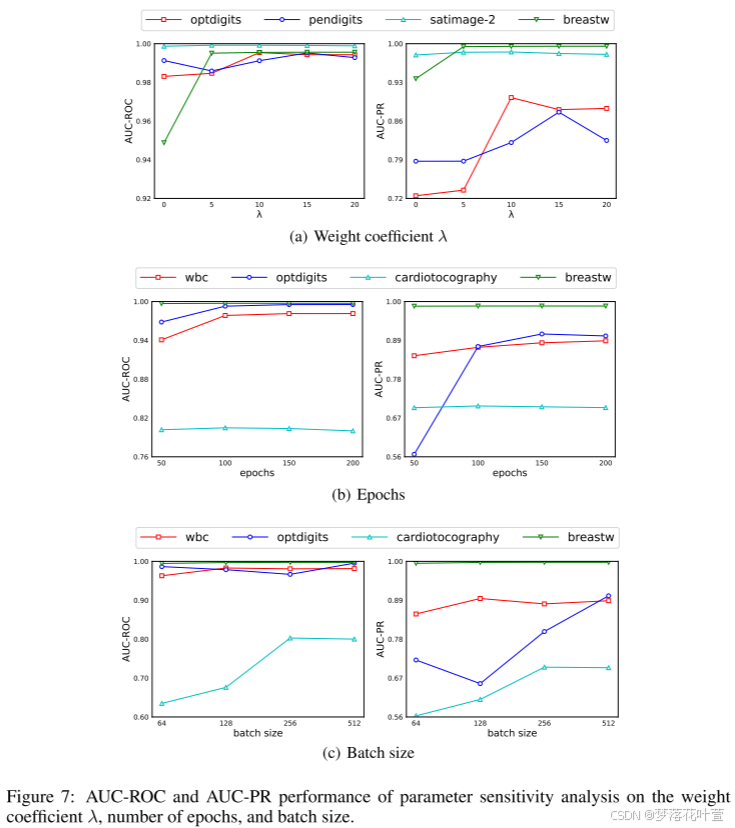
• 图7显示了权重系数$\lambda$、epoch数和batch size参数敏感性分析的可视化。 结果与第4.5节一致，即模型对参数不敏感。

• 图8可视化了四个数据集上不同异常污染比例的AUC-ROC和AUC-PR表现:breast, Cardio, Cardiotocography和Wbc。 如第4.5节所述，与其他三种自监督方法相比具有较强的鲁棒性。

5 Discussion

讨论MCM的可解释性，MCM可以从两个方面提供可解释性:特征之间的相关性和单个特征的异常。 每个样本异常评分的计算有两次平均操作。第一个是在不同的特征上平均，第二个是在不同的遮罩版本上平均。作者将一个遮罩版本跨不同特征的平均重构误差定义为每个遮罩的贡献，将一个特征跨不同遮罩版本的平均重构误差定义为每个特征的贡献。

• 特征之间的相关性

特征之间的相关性由 MCM 中的不同遮罩表示。这意味着每个遮罩捕获了数据中不同特征之间的某种特定关系。每个遮罩的贡献可以通过指出样本偏离正常数据中存在的特征相关性来提供可解释性，通过分析每个遮罩的贡献，可以解释一个样本与正常数据相比，在哪些特征相关性上存在偏差。这种分析可以帮助读者理解样本为何被分类为异常。

作者参考了Shenkar & Wolf (2022)的研究，进行了一个案例研究。在这个研究中，正常数据是在四维空间（R4）中通过高斯分布采样的向量。协方差矩阵显示特征1和特征4之间的协方差很高（0.85），而其他特征之间的协方差为零。这意味着在正常数据中，特征1和特征4是高度相关的；异常数据是从类似的分布中采样的，但是在任何特征之间都没有相关性。这意味着异常数据打破了正常数据中的特征相关性模式。

更进一步的，作者设置了四个遮罩，随机选取了一个异常样本，计算了这个异常样本对应的每个遮罩的贡献比例：[39%, 14%, 7%, 40%]，并可视化了它的遮罩。表明第1个和第4个遮罩对这个异常样本的贡献最大。这两个遮罩的较高贡献说明该样本的第1维特征和第4维特征之间的相关性与正常数据的相关性不同。

• Each individual feature

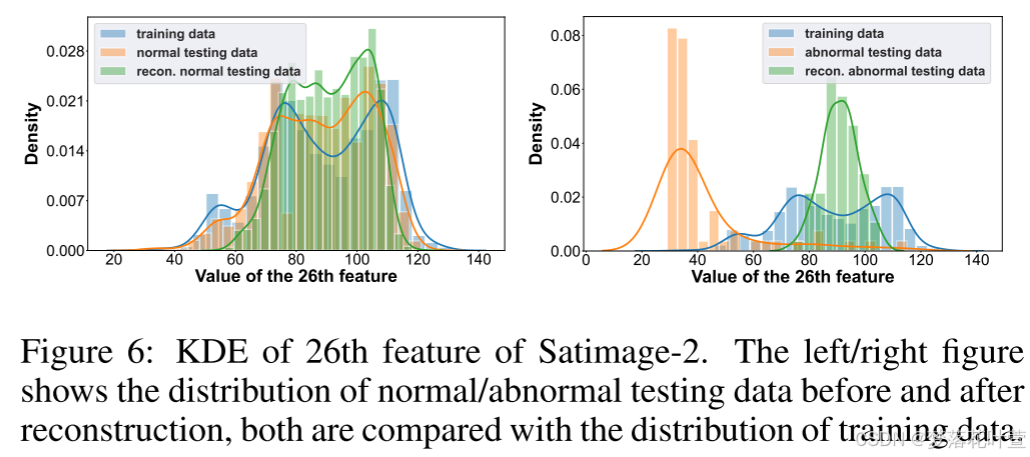
图6绘制了Satimage-2数据集的第26个特征的KDE。 左/右图显示了重建前后正常/异常测试数据的分布，所使用的重建数据是所有屏蔽版本的平均值。 如图所示，正常测试数据重构前后的分布差异不大，与训练数据的分布基本一致。 然而，对于异常测试数据，重构后的分布显着偏向训练数据。 由于MCM在训练时只访问正常数据，它会隐式学习正常数据每个特征的经验边缘分布，并且更倾向于将屏蔽特征重构为该分布，因此分布远离训练数据的异常样本相比会具有更大的重构误差。

人话就是正常的重构后偏离不大，异常的重构会偏向正常，但这个时候就会出现很大的偏差了。

基于上述定性分析，作者对甲状腺数据集进行了定量研究，该数据集有六个特征：[TSH、T3、TT4、T4U、FT1、TBG]。 通过计算所有异常的平均单个特征贡献并获得相应的结果：[16%, 43%, 1%, 9%, 11%, 9%]。 单个特征贡献最高的两个为“T3”（43%）和“TSH”（16%）。 这些结果对于医学疾病检测具有实际意义，因为甲亢的特点是“T3”水平升高和“TSH”水平降低。 因此，单个特征的贡献可以补充每个遮罩的贡献，并从单个特征的角度提供可解释性。

附录D轻量级解码器和纯遮罩预测，前面给过了

附录G是遮罩的可视化

图 9 显示了一个正常样本的遮罩，正文里出现过了。图 10 显示了包含和不包含多样性损失的遮罩的比较。 视觉分析表明，当包括多样性损失时，遮罩多样性显着增加。 相比之下，没有多样性损失的遮罩表现出值集中在 0.5 左右，表明独特性较低。 使用多样性损失有助于捕获正常数据中存在的多样化相关性，从而有助于检测异常。

附录H是遮罩退化学习的讨论

首先，作者将遮罩退化问题定义如下：对于为样本生成的遮罩向量，所有值都为1，则没有任何东西被遮罩，表明发生了遮罩退化。 此外，可以将退化问题扩展到遮罩向量中的值非常接近甚至相同的情况。 这是因为在这种情况下，遮罩对输入的影响更像是均匀缩放，而不是选择性地遮罩某些特征并用其他特征重建它们。 因此，这种现象也可以认为是遮罩退化的发生。

作者对这个问题进行了定性和定量实验。 定性结果见图 9，可以观察到，当不应用多样性损失时（即右图），超过一半的遮罩向量表现出退化问题，其中所有遮罩值都是相同的。 当使用多样性损失进行训练时（左图），没有一个遮罩向量表现出这个问题，并且遮罩之间存在显著的多样性。 对于定量结果，使用遮罩向量和均匀分布之间的 KL 散度来定义退化程度。

其中$u$表示均匀分布，$m$是长度为$F$的掩模向量。这个表达式的直观解释是，随着遮罩向量的值越接近，它们与均匀分布的KL散度就会越小，表明退化越严重。 以Breastw数据集的样本为例，在有和没有多样性损失的情况下训练时，退化度分别为9.0724e-06和0.8730。 这表明在多样性损失的约束下，MCM可以有效避免遮罩退化问题。