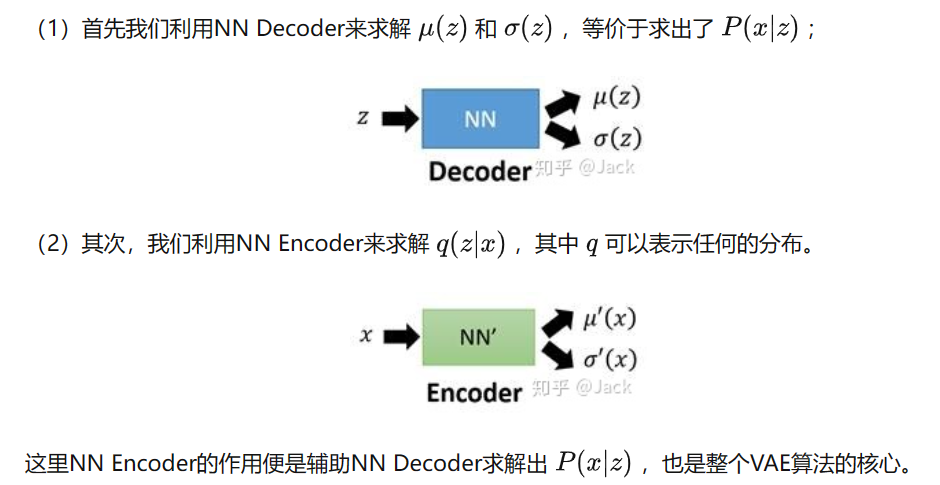
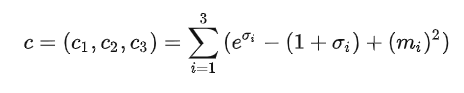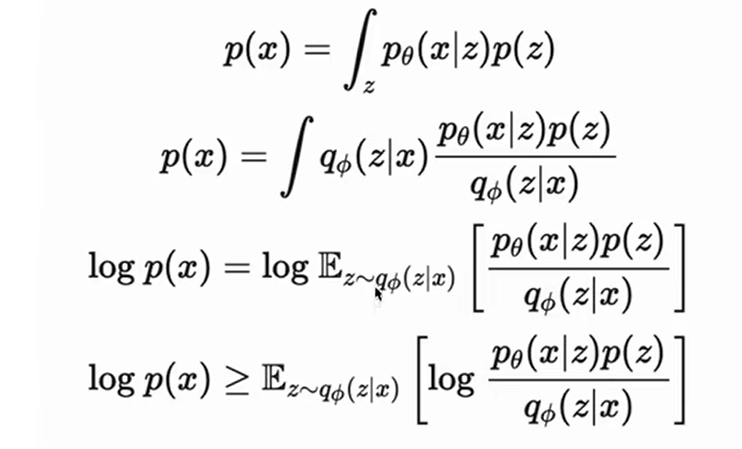无监督学习之VAE——变分自编码器详解
机器学习方法—优雅的模型（一）：变分自编码器（VAE）

无需多言，看这两篇文章即可。本文主要是总结一下我在看这篇文章和其他视频时没能看懂的部分解读。

看这里看这里！

以防有人不看前言，我再重申一遍，看这两篇文章：无监督学习之VAE——变分自编码器详解
机器学习方法—优雅的模型（一）：变分自编码器（VAE）

一些名词解释

NN是神经网络neural network的简写。

latent code可以翻译为潜在编码

dim代表dimension维度

PCA是主成分分析，在我的PCA和SVD文章中介绍了这两种降维方法。

Conv是convolution卷积的缩写

BN是Batch Normalization批标准化，在神经网络中需要使用标准化保持输入和输出的相同分布，批标准化把数据分成小批小批进行随机梯度下降，而且在每批数据进行前向传递 的时候，对每一层都进行 normalization的处理。在每一个全连接层和激励层之间都需要连接一个BN层进行标准化。

RBM是受限玻尔兹曼机Restricted Boltzmann Machine，RBM的结构只有两层，显形层和隐性层。从结构上看，RBM很像一个两层的神经网络，但与神经网络不同在于 RBM不光只有反向传播，而是显层和隐层之间互相影响，互相传播。同时，RBM的值都是二值的，这意味着，每一个因素只有0 或 1 两种可能的值。如上图所示

鲁棒性，这个翻译我也是醉了，也能被翻译为健壮性（耐艹性 ），就是指系统在内部结构发生扰动的情况下，外部干扰抵御能力的保持能力。或者说是稳定性的强壮性。

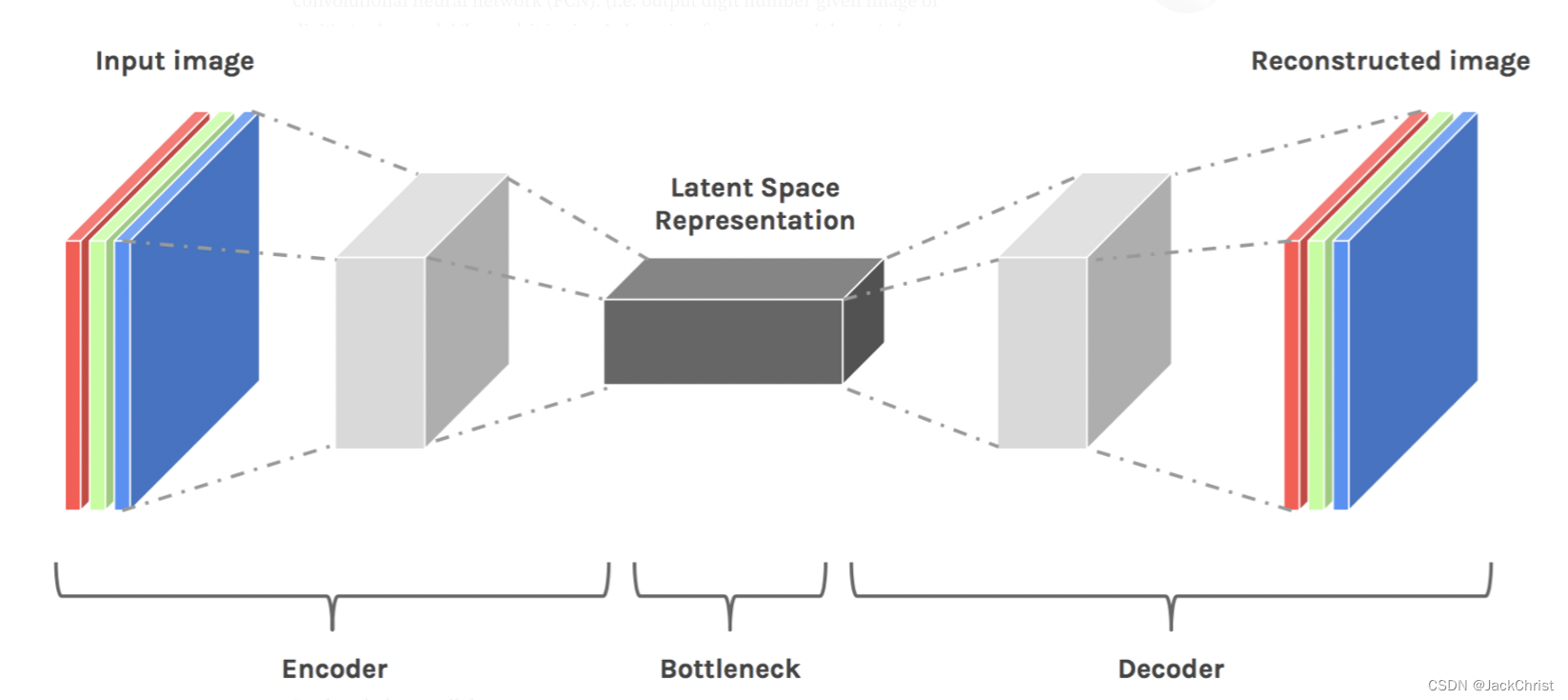
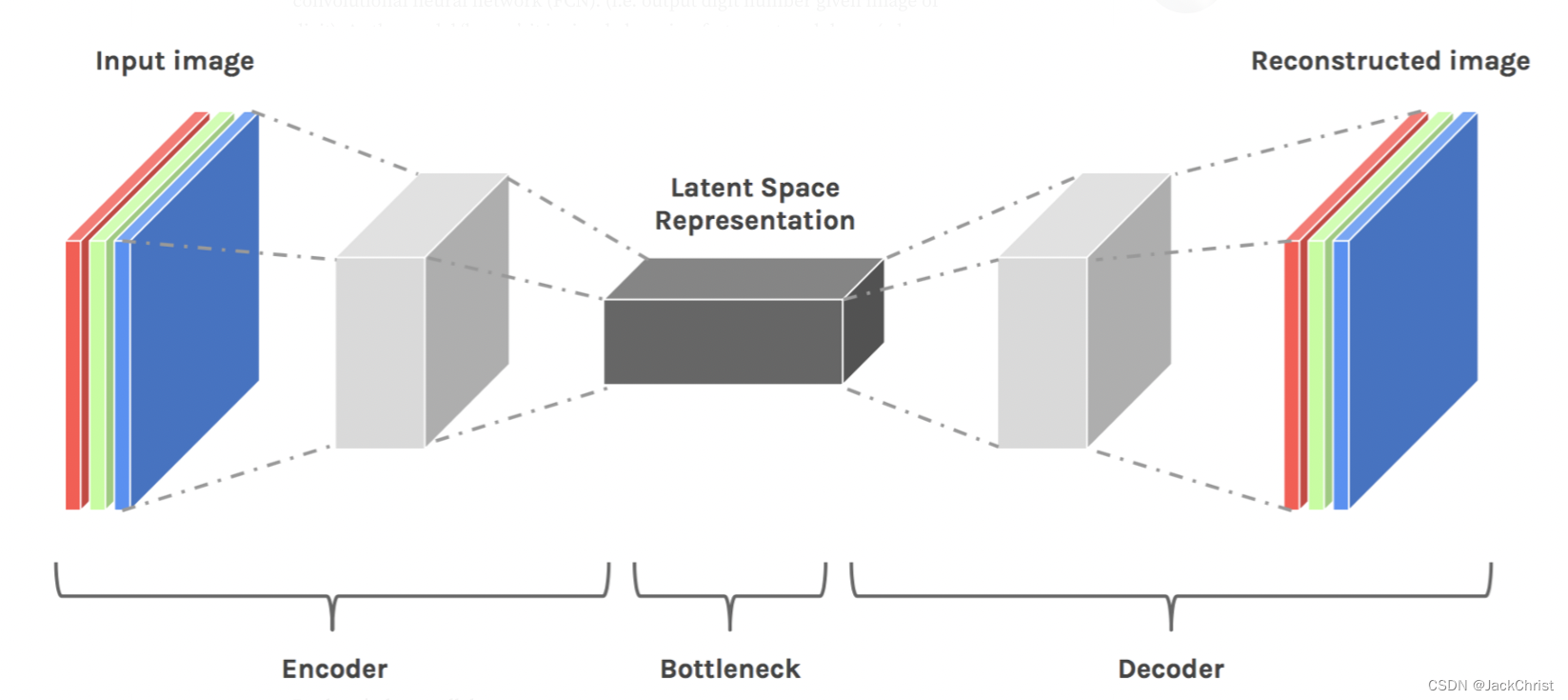
Bottle，一个很有意思的概念，我们可以类似地将整个AE网络看作为一个花瓶（形状上），中间最细的潜在空间部分被我们称为花瓶的瓶颈（Bottleneck），如下所示：

潜在编码

参考笔记：快速理解深度学习中的latent code潜在编码
（Latent Space）理解机器学习中的潜在空间

什么是潜在编码？潜在编码你可以理解为一种降维或者压缩数据的方式，旨在用更少的信息去表达数据的本质。例如我们在将核函数的时候提到了核技巧作为一种升维方法，其本质是将非线性的原始空间的特征点通过核函数的变换送入到高维特征空间转化为线性问题，新得到的这个高维空间也可以理解为一种潜在空间。在我们讲到AE的例子中，潜在空间是对原空间进行了降维的空间，通过encoder这一变换我们得到了潜在编码。

上图是一个简单的encoder-decoder架构，如果把整个网络看成一个花瓶，最细的地方则称之为瓶颈。当降维时，我们认为这是有损压缩的一种形式，如果损失的是噪声或者是无用信息是我们最喜欢的了（这样就可以达到信息压缩的目的）

通过encoder压缩之后，更重要的是恢复，我们理应认为，能恢复的才算成功压缩了的，那么我们就可以认为这个latent space representation是真的表达出了input image中最关键的信息。

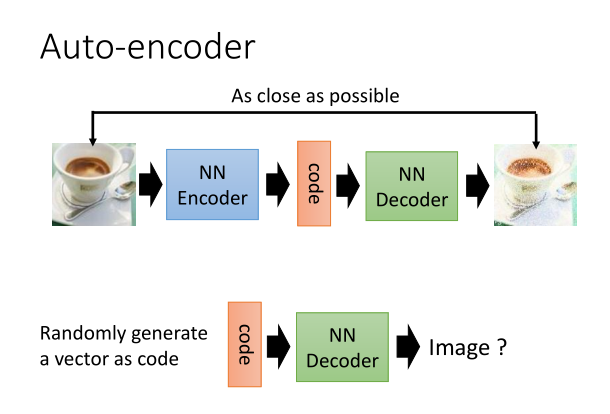
不过AE在原理上看更像一个可压缩杯，通过encoder将其拍扁到latent space得到latent code，再通过decoder将其展开为reconstructed image，实际上得到的output和input相差并不是很大。如果得到的结果和原来的结果相似，那么AE本身就不适合作为生成模型，尤其是我们想要得到其他图像的时候。

同类潜在编码相似

我们要理解神经网络是如何定义同类的，例如椅子和椅子，上图中黄色椅子和黑色椅子在我们认知的定义里是同类，但是如果在网络中用特征来表示，那么黄色椅子包含的特征：{椅子的一些特征，个性化的特征，黄色}。黑色椅子的特征：{椅子的一些特征，个性化的特征，黑色}。想象一下在特征空间中如果特征作为点分布在空间内，那么黄色椅子和黑色椅子的特征分布近似程度并不会特别高（包括颜色，形状，结构等一些个性化的特征都影响了两个分布的近似程度）。假如我们压缩到潜在空间，例如去掉了那些个性化的特征，仅仅保留了“椅子的一些特征”，那么在潜在空间上的两个椅子的特征分布就十分相似了，因此网络就认为这两个椅子当然是同类。

通过学习边缘，角度等的图案，这些都可以被我们的模型“理解”。如所解释的，这样的特征被包装在数据的潜在空间表示中。因此，随着维数的减少，与每个图像截然不同的“外部”信息（即椅子颜色）从我们的潜在空间表示中被“去除”，因为只有每个图像的最重要特征都存储在潜在空间表示中。 结果，随着我们减小尺寸，两把椅子的表示变得越来越不清晰，越来越相似。如果我们想象它们在空间中，它们将“紧密”在一起。

因此寻找潜在空间是我们学习的重要步骤，而非粗暴地直接计算两个图像像素间的欧式距离。

如果去掉的特征太多，那么也许网络会认为椅子和桌子也是同类，毕竟大家都四只脚。

潜在空间插值

同类在空间中是相近的，例如两把椅子的向量为[0.1,0.1]和[0.12,0.12]，把这两个喂入网络中，生成的当然是椅子，那如果输入[0.11,0.11]呢？当然也是椅子，这就是插值。也就是说在对应的区间内取值latent code，那么最终解码的结果当然和想要的结果是近似的。下图展示了插值的效果（横向和纵向都是不同结果的插值），我们可以通过在潜在空间上进行插值，并使用模型解码器将潜在空间表示重构为二维图像，并以与原始输入相同的尺寸来生成不同的面部结构。可以看到同类周围插值就相似但有微小区别的。最简单的应用就是把它当成一种数据增强去扩大数据集。

（上图是用VAE训练的宝可梦图像，我们发现中间的插值中确实有一些像是真正的宝可梦，我们期望的生成结果就是这样的）

下图为两把椅子之间进行线性插值的效果图。可以看到随着插值的改变最终的生成结果会呈现出一种线性的变化效果。

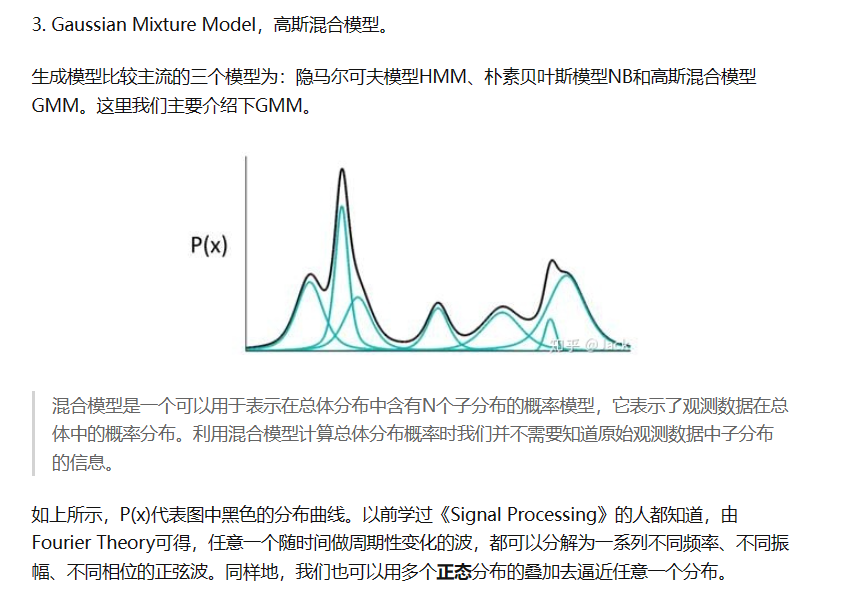
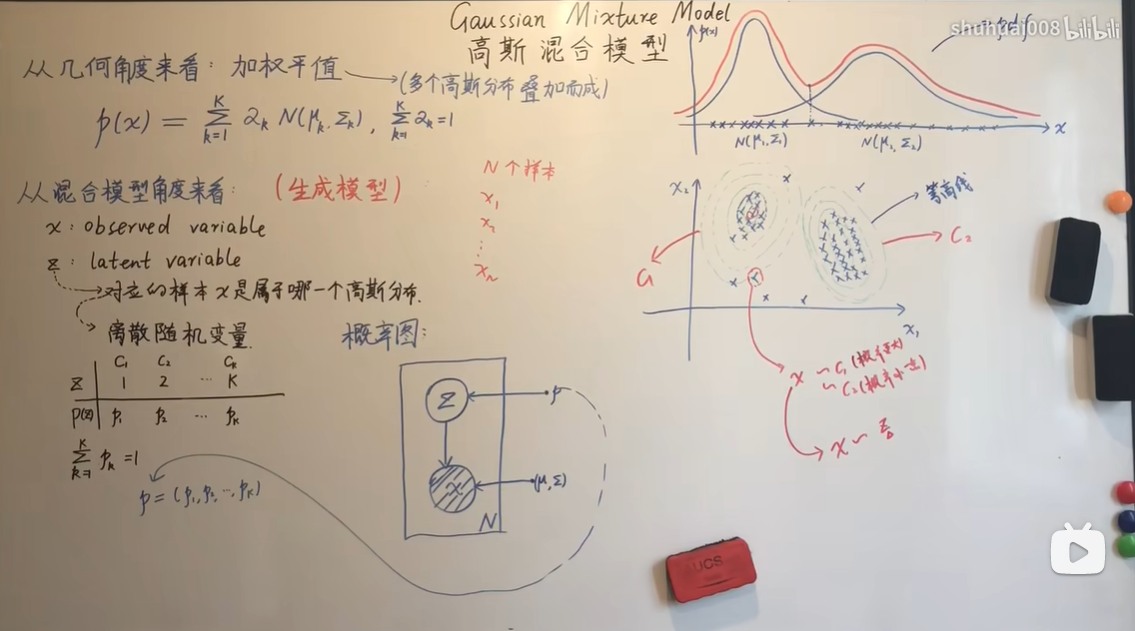
高斯混合

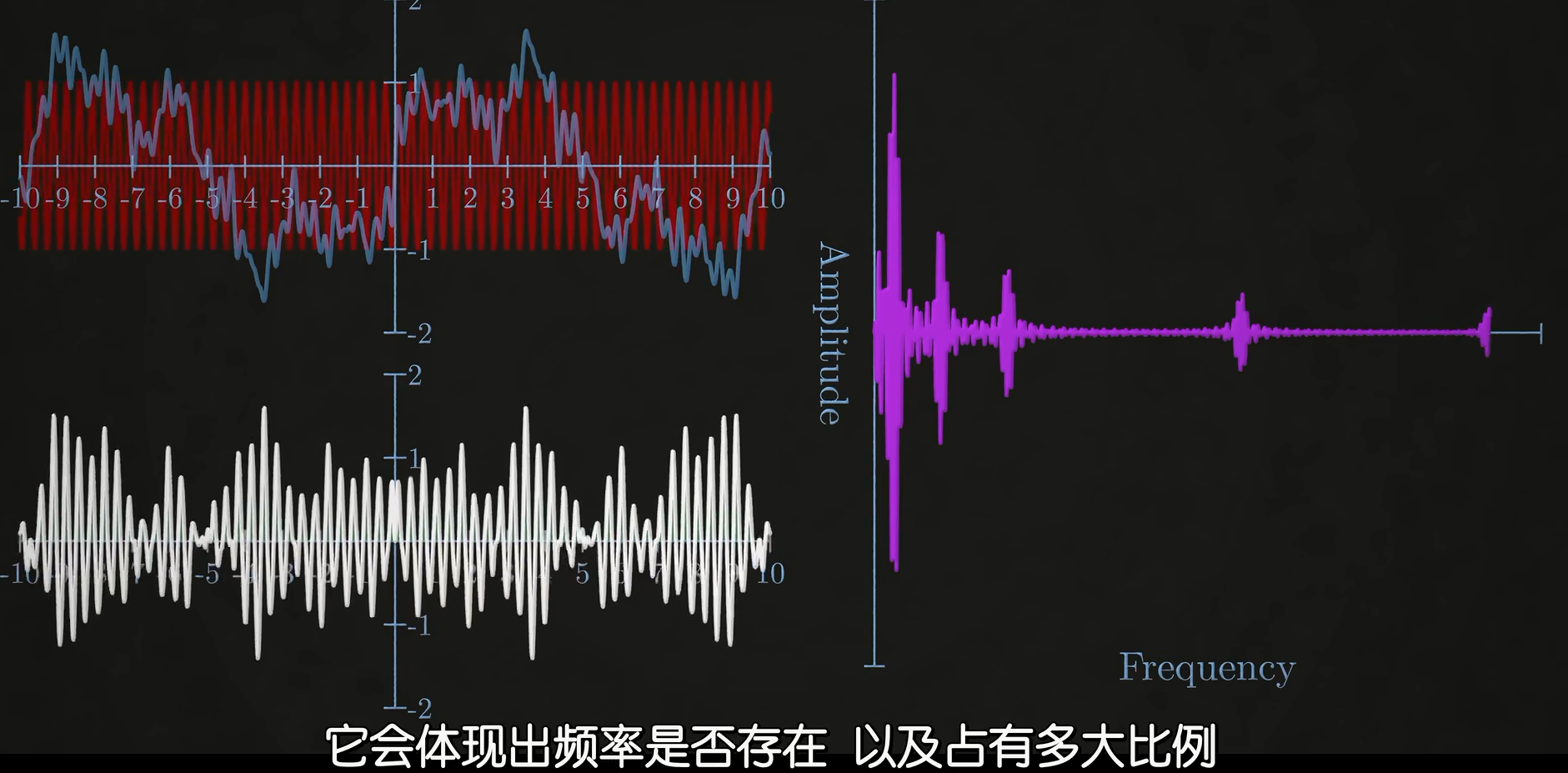
在我们在卷积网络前序讲傅里叶变换的时候，曾经提到过一些关于信号的知识。一个信号可以被分解为不同频率，振幅，相位的正弦波叠加，那么相似的，混合模型的总体分布可以被分解为多个子分布的模型叠加，因此我们可以用多个正态分布的叠加去逼近任意一个分布.

增加层数的AE

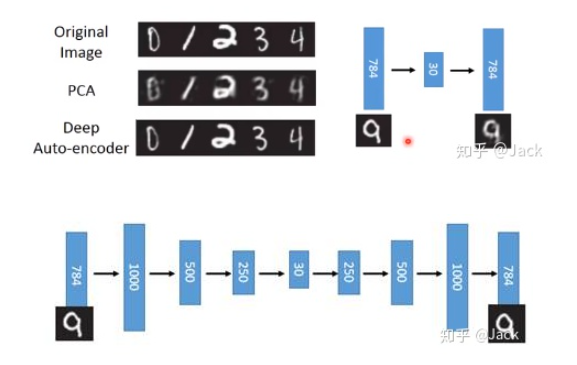
原文中给出了上面这个图，上半部分的右边所示模型代表了原始的单层AE，我们可以看到效果并不是很好，AE先将784像素的输入压缩为30像素的latent code再用decoder 重建（reconstucted）为784像素，输出结果很模糊，因为我们只使用了一层hidden layer进行学习，效果肯定是很差的。

下半部分是一个增加了层数的Deep AE，其中有宽度增加例如784像素拓宽到1000像素，也有深度增加例如增加了若干层hidden layer。原文中的一句话很好了概况了神经网络深度和宽度增加的优点：网络越深，能够学习到更加抽象的高级语义特征；而网络越宽，则能够让每一层的hidden layer学习到更加丰富的特征表示。因此我们可以看到最后的输出结果要比输入结果看起来更清晰了，说明效果很好，上半部分中左边给出的Deep AE对于原始图像处理后的MNIST结果也证明了这点。

AE的局限性

上面我们通过AE构造出一个比PCA更加清晰的自编码器模型，但这并不是真正意义上的生成模型。对于一个特定的生成模型，它一般应该满足以下两点：

（1）编码器和解码器是可以独立拆分的（类比GAN的Generator和Discriminator）；

（2）固定维度下任意采样出来的编码，都应该能通过解码器产生一张清晰且真实的图片。

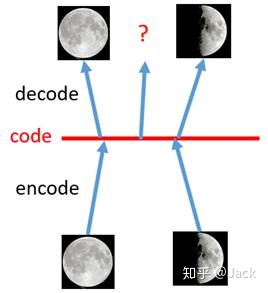
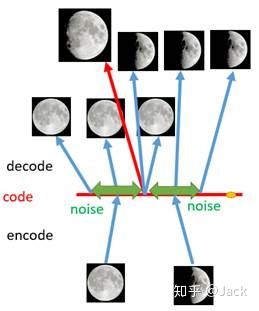
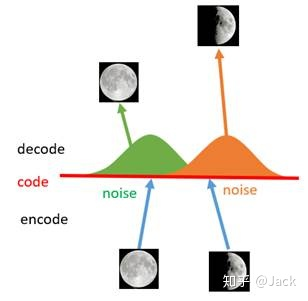
所以为什么我们说AE并不是生成模型，让我们以第二点为例，如下图所示，我们用一张全月图和一张半月图去训练一个AE，经过训练，模型能够很好地还原出这两张图片。接下来，我们在latent code上中间一点，即两张图片编码点中间处任取一点，将这点交给解码器进行解码，直觉上我们会得到一张介于全月图和半月图之间的图片（比如阴影面积覆盖3/4的样子）。然而，实际当你那这个点去decode的时候你会发现AE还原出来的图片不仅模糊而且还是乱码的。

（假设AE能够还原出全月图和半月图，那么按照直觉，如果上图中左边code点能解码出全月图，而右边code点能解码出半月图，那么我们在其中选取的任意code点就能解码出一个介于全月和半月之间的月亮，然而实际情况并不是这样，AE还原出来的图片不仅模糊而且还是乱码的。）

为什么会出现这种现象？一个直观上的解释是AE的Encoder和Decoder都使用了DNN（深度神经网络），如果说这个神经网络是一个线性变换的话，那么是可以实现上述的直觉判断的，但是神经网络并不会全是线性变换（这一点我们之前的文章解释过，如果所以hidden layer都是线性变换，那么一层神经网络和多层神经网络并无本质区别），而DNN是一个非线性的变换过程，因此在latent space潜在空间上点与点之间transform往往没有规律可循。

如何解决这个问题呢？一个思想就是引入噪声，扩大图片的编码区域，从而能够覆盖到失真的空白编码区。其实说白了就是通过增加输入的多样性从而增强输出的鲁棒性。当我们给输入图片进行编码之前引入一点噪声，使得每张图片的编码点出现在绿色箭头范围内，这样一来所得到的latent space就能覆盖到更多的编码点。此时我们再从中间点抽取去还原便可以得到一个我们比较希望得到的输出，如下所示：

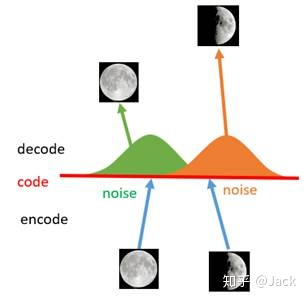
之所以加噪能够产生这样的效果，是因为噪声使得latent space能够覆盖到比较多的区域，但是还是有不少地方没有被覆盖到，比如上图右边黄色的部分因为离得比较远所以就没编码到。因此，我们是不是可以尝试利用更多的噪音，使得对于每一个输入样本，它的编码都能够覆盖到整个编码空间？只不过这里我们需要保证的是，对于源编码附近的编码我们应该给定一个高的概率值，而对于距离原编码点距离较远的，我们应该给定一个低的概率值。没错，总体来说，我们就是要将原先一个单点拉伸到整个编码空间，即将离散的编码点引申为一条连续的接近正态分布的编码曲线，如下所示：

给AE添加噪声的模型，被我们称为VAE变分自编码器。VAE中噪声和潜在空间之间的关系是将噪声添加到输入数据，然后由编码器将输入数据映射到潜在空间表示。然后解码器使用该潜在空间表示来生成输出数据。也就是加噪使得latent space覆盖到更大的编码空间，使得我们能在code中间插值从而得到一个新的生成结果，也可以将code上的分布看作不同结果之间的正态分布的高斯混合。

VAE的模型架构

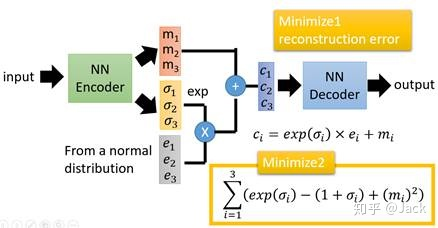
在上面我们也介绍过了，VAE就是在原本的AE结构上，给编码添加合适的噪声。首先我们将input输入到NN Encoder，计算出两组编码：一组编码为均值编码$m$,另一组为控制噪声干扰程度的方差编码$\sigma$，方差编码$\sigma$主要用来为噪音编码$z=(e_1,e_2,e_3)$分配权重，为了使得NN的权重是非负的，我们还要对$\sigma$进行一次e指数运算，我们计算出$c_i=exp({\sigma }_i)\times e_i+m_i$。最终还需要多加上这个loss损失函数c，最终结果还要对其以及reconstruction error最小化：

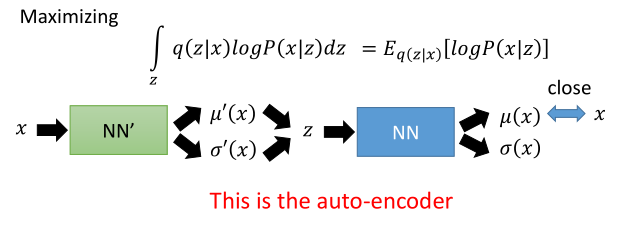
最后，我们将原编码m和经过权重分配后噪声编码进行叠加，就得到了新的latent code，然后再送入NN Decoder。现在我们先不讨论这个loss是怎么得到的，让我们看看它的作用：

如果不添加这个损失函数，那么模型为了保证所生成出来的图片质量越高（因为我们最小化了reconstruction error），那么编码器肯定希望噪声对自身生成的图片的干扰越小越好，于是分配给噪声的权重越低越好。如果不加约束限制的话，网络只需要将方差编码设置为接近负无穷大的值，$\sigma \to -\infty ,则e^{\sigma }\to 0$。最后也就相当于没有引入噪声，那还弄个锤子的VAE，结果上来看它训练得很好，但是往往生成的图片很差。

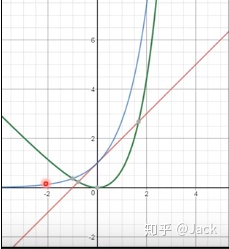
逆向思维思考完，我们再来正面的理解下，为什么加入这个辅助的loss就有用？公式怎么得到的后面再讨论。现在我们根据上面给出的公式对$\sigma$进行求导，可得$c=e^{\sigma }-1$，令其等于0可知当$\sigma =0$时取到极小值，这样一来便可以约束方差编码不会一路开挂似的走向负无穷大，相当于起到正则化约束的作用。

蓝线代表了$e^{\sigma }$,红线是$(1+\sigma )$,用蓝线减去红线就是图中的绿线$e^{\sigma }-(1+\sigma )$，我们可以看到最小值为噪声参数$\sigma$为0时，值为0，而若$\sigma$趋向负无穷则其loss值反而会增大，所以限制了最小化噪声参数对模型的影响。

原文中举的一个例子很有意思，我将其改写一下：如果单纯只是想要考高分，那只要把题目的知识点难度系数（噪声参数）降得很低就好了，最低就是无穷小，但是不符合难度的考试并不是老师们想要的，因此我们需要一个出题老师（loss损失函数），难度系数低没关系，我出题人直接用低难度系数搞一个高计算量的题目，那题目不就难起来了吗？为了保证考试（网络）的难度始终在线，就是恶心你。

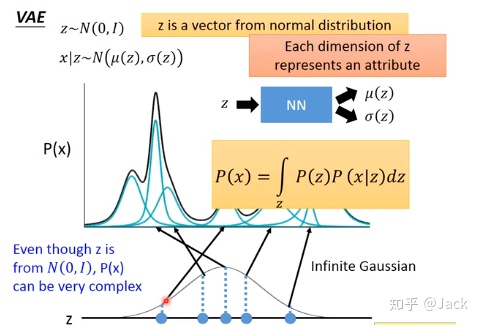
选择VAE，我们来看看在潜在空间上得到的关于code的概率混合分布，会发现一个很有趣的现象，在高点我们可以得到一些真正的宝可梦输出，例如上图的妙蛙花，喷火龙等，而在低点则是一些模糊的生成图像，效果并不是很好。如果我们在插值中能找到一些高点，那么就能够生成一些真正的宝可梦图像。

VAE原理

（原文中这里讲的不太清楚，我想进行一些扩充）
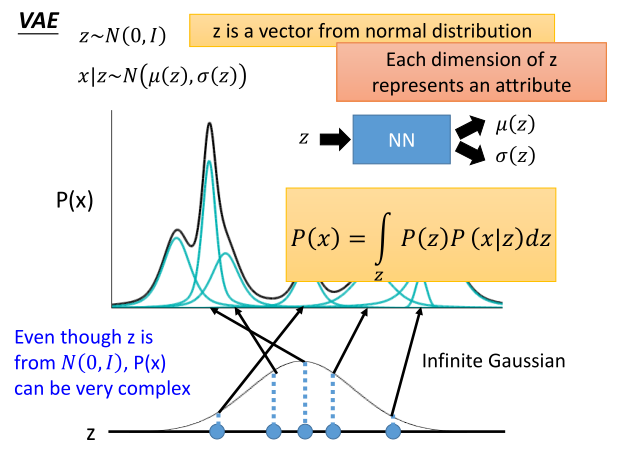
之前谈到高斯混合的时候我们说任意的分布可以用n个正态分布的混合来逼近，所以让我们从标准正态分布取样$z$,然后进行混合。但实际上我们并不是单纯地取几个正态分布，正如上图所示，我们发现对应的采样点实际上给出的高斯分布是非正态的，需要给NN之后得到$\mu (z)和\sigma (z)$。

这种方法被我们称为重采样技巧，之所以使用这个技巧是为了解决$z$是latent variable的问题。因为如果直接使用正态分布的表达式，我们想要得到符合高斯分布的$z\sim N(\mu ,{\sigma }^2),$一个是积分不好求，二是没法写出显式的函数关系式，没法写出显式的函数关系式，那就没办法做反向传播。因此我们可以先对正态分布采样$z^{\prime }\sim N(0,I)$,然后将$z=\mu +\sigma z^{\prime }$。那么z就可以显式地写出函数，$\mu$和$\sigma$就成了参数，$z$就成了output，$z^{\prime }$就是input,我们就可以通过一个神经网络来学习这个$z$了，其效果等价于直接从$N(\mu ,\sigma )$中采样了$z$。对应到上面的NN中就是$z$取样正态分布直接输出了两个高斯分布的参数$\mu (z),\sigma (z)$

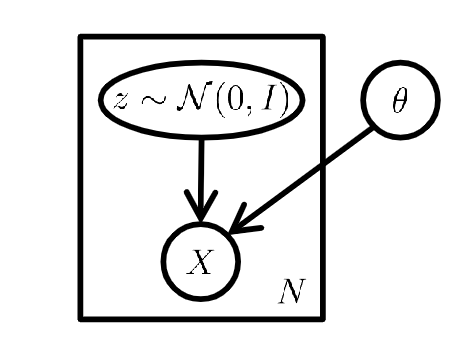
我们可以给出上面的概率图模型，其中$z$是满足正态分布的采样点（例如$z_1,z_2...z_n$都是满足正态分布的），X代表我们根据采样确定的高斯分布，$\theta$代表了高斯分布中的参数$\mu ,\sigma$。重复$N$次就能得到混合高斯分布。

我们看右边对混合高斯分布表示为二元正态分布的等高线图，明显可以看到样本的分布可以分为两个高斯分布$c_1,c_2$,注意红点处样本，该点既可以算是服从$c_1$分布，也可以算是服从$c_2$分布的，不过从概率上来看服从$c_1$的概率更大。一个比较好的表示方法是$x\sim z$，z的概率密度可以表示出x服从这些分布的概率。而混合高斯，更应该是多个高斯分布的加权平均。

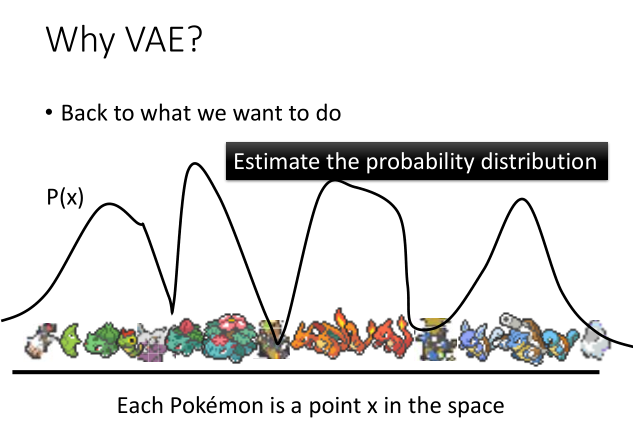
回到VAE的模型结构，在这个架构下，我们可以认为数据集是由某个随机过程生成的，而$z$是这个随机过程中的一个不可观测到的隐变量。这个生成数据的随机过程包含两个步骤：

1.从先验分布$p(z)$中采样得到一个$z_i$
2.根据$z_i$,从条件分布$p(x|z_i)$中采样得到一个数据点$x_i$
(在神经网络中我们将利用重采样技巧计算对应的高斯分布)

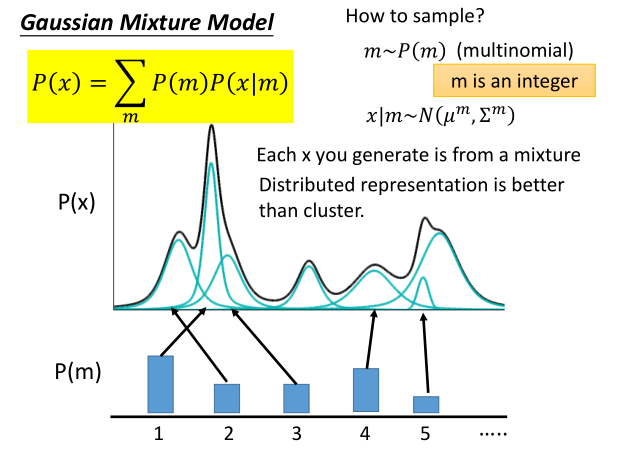
我们对P(X)这个分布随机采样$m$个离散点，其中每采样一个点$m_i$，我们将其对应到一个高斯分布$N({\mu }^m,{\sigma }^m)$，于是一个多项式分布利用混合模型就可以表示为：

$P(x)=\sum _{m}P(m)P(x|m)={\int }_{z}P(z)P(x|z)dz$

这里，$m\sim P(m)$，$x|m\sim N({\mu }^m,{\sigma }^m)$。从公式变换中我们发现，原来对样本的离散取样$\sum _{m}P(m)P(x|m)$，可以转化为关于噪声z的连续采样${\int }_{z}P(z)P(x|z)dz$。正对应了下图：

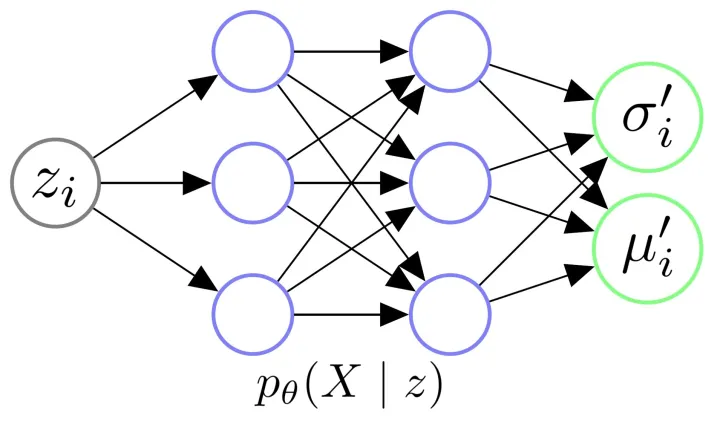
经过以上操作，我们便可以将原先离散的、存在大量失真区域的编码方式，转换成连续有效的编码方式。这里$P(x)$是已知变量，$P(x|z)$是未知变量，由于$x|z\sim N(\mu (z),\sigma (z))$，所以问题转化为求$\mu$和$\sigma$的表达式

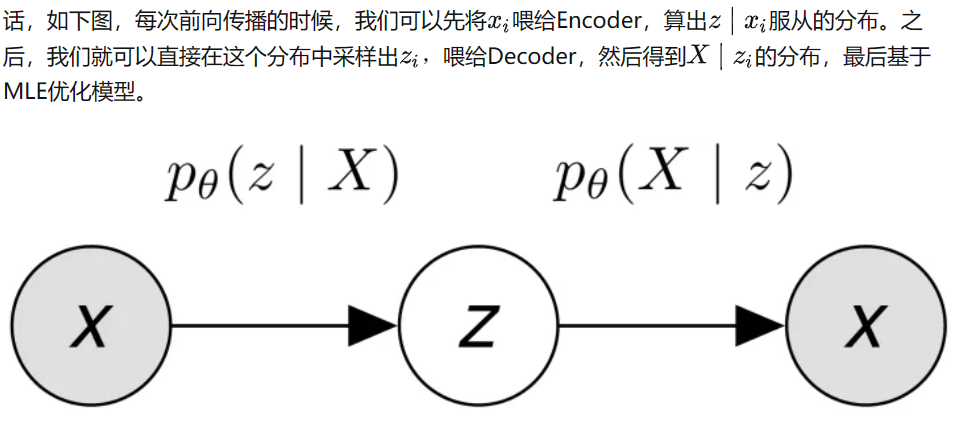
让我们放大Decoder的架构，我们给Decoder输入一个从正态分布中采样得到的$z_i$,其实是希望由$\theta$参数化的Decoder能够学会一个映射，输出$z_i$对应的X分布，即$p_{\theta }(X|z_i)$

公式推导

在编码器的推导部分中给出了上面的证明过程，有些细节可以补充一下，例如:
$logP(x)=logP(x)\times 1=logP(x){\int }_{z}q(z|x)dz$，由于$logP(x)$与$z$无关，因此
$={\int }_{z}q(z|x)logP(x)dz$,其中$\frac{P(z,x)}{P(z|x)}$是贝叶斯公式得到的，随后推导出后面的式子

复习一下KL散度的公式：$D_{KL}(p||q{)}_{=}\sum _{i=1}^{n}p(x)log\frac{p(x)}{q(x)}$，右边部分可以表示为KL散度

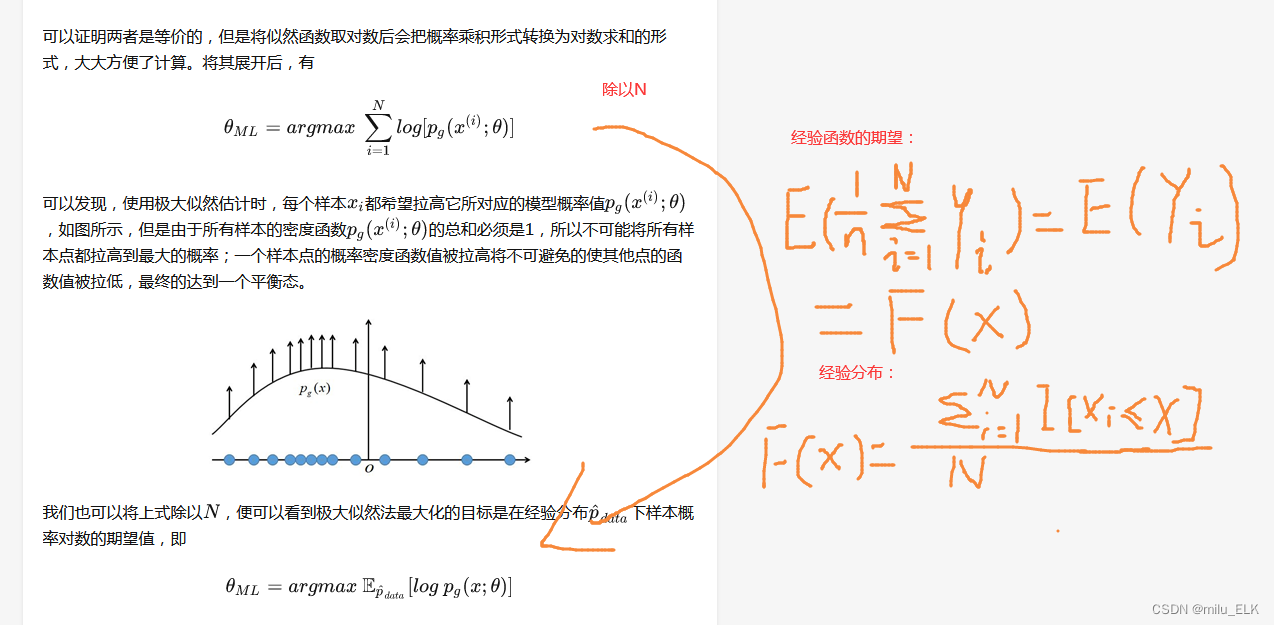
在我看另一个视频的时候给出了下面的式子，上下两个式子是等价的：

上图中积分少了$dz$，且省略了KL散度，并且表示为了期望的形式，刚开始我还疑惑这是怎么变形的，后来发现我们是讲过这部分内容的：

也就是分布的求和形式可以转化为对应分布的期望。这里只是稍微提一下，我个人认为还是第一个给出的式子要更好。

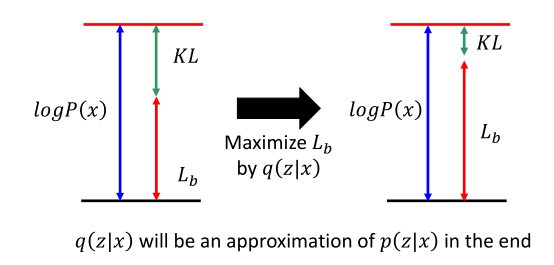
现在我们找到了$logP(x)$的一个下界:

$logP(x)\ge {\int }_{z}q(z|x)log(\frac{P(x|z)P(z)}{q(z|x)})dz=L_b$

带入原式子，可写成：$logP(x)=L_b+D_{KL}(q(z|x)||P(z|x))$,也就是将求$P(x)$转化为同时求$P(x|z)$和$q(z|x)$的问题，我们观察一下$logP(x)$和$L_b$的关系：

由于$P(x)={\int }_{z}P(z)P(x|z)dz$，所以当$P(x|z)$固定时，由于$P(z)$是固定的,所以蓝色线段处的$logP(x)$是定值。而等式给出$logP(x)=KL+L_b$，因此如果最大似然需要最大化$L_b$的话，根据$L_b$的公式就需要最大化$q(z|x)$，最后得到右边的结果，则$L_b$尽可能大，KL尽可能小（又讲到了最大似然相当于最小KL散度）。直到KL散度近似于0，则$L_b=logP(x)$,最终$q(z|x)$和$P(z|x)$这两个分布会完全近似。

也就是说求解最大似然$MaxlogP(x)=Max{L}_b$,从宏观角度来看$x|z\sim N(\mu (z),\sigma (z))$，调节$P(x|z)$就是调节NN Decoder；相反的，$z|x\sim N({\mu }^{{}^{\prime }}(z),{\sigma }^{{}^{\prime }}(z))$,调节$q(z|x)$就是调节NN Encoder。

因此VAE模型的算法便是：Decoder每改进一次，Encoder就调节成跟其一致，并且利用约束项迫使Decoder在训练的时候“只能前进，不能后退”。

Decoder的结果也同理，则$L_b=-D_{KL}(q(z|x)||P(z))+{\int }_{z}q(z|x)logP(x|z)dz$,

我们将右式的左半部分记为$-A^{\ast }$,右半部分记为$B^{\ast }$，即$L_b=-A^{\ast }+B^{\ast }$。因此$Max{L}_b$相当于求$A^{\ast }$的最小值和$B^{\ast }$的最大值。

$A^{\ast }$我们是希望它尽量小的，在展开后就成了约束项损失函数。
上面的期望的含义可以表述为：在给定NN Encoder输出$q(z|x)$分布的情况下，为了取得最大的$B^{\ast }$，则解码器Decoder的$P(x|z)$值要尽可能的高。如果不考虑方差的话，这其实就类似于一个Auto-Encoder的损失函数。

（不考虑方差，那么整体结构其实就相当于AE）

局限性

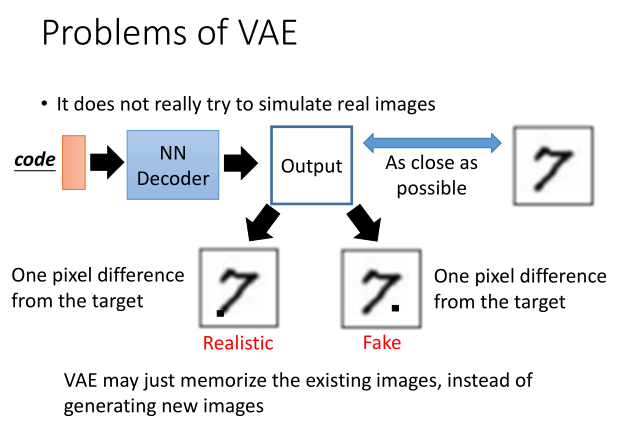
一个重要的局限性就是：VAE并不是真的在生成新的图像，它只是在记住的那些已有图像中进行插值生成，最终的结果也会与已有图像存在相当的相似度。

虽然VAE比普通的AE模型训练出来的效果要好很多，但是训练过VAE模型的人都知道，它生成出来的图片相对GANs那种直接利用对抗学习的方式会比较模糊，这是由于它是通过直接计算生成图片和原始图片之间的均方误差，所以得到的是一张“平均图像”。

2. What’s the difference between VAE and AE?

（1）AE中隐层表示的分布是未知的，而VAE中隐变量是服从正态分布的；

（2）AE中学习的仅仅是NN Encoder和Decoder，而VAE还学习了隐变量的分布，即高斯分布的均值和方差；

（3）AE只能从1个样本x，得出对应的重构过的x；而VAE学习了隐变量z所服从的高斯分布的参数，便可以源源不断地产生新的z，从而生成新的样本x。

总结

VAE通过给AE引入噪声，将潜在空间中的code从离散区间转化为了连续区间，从而我们可以在连续区间中取得code的插值来生成一些介于某些训练结果code之间的样本。这些样本和原来的输入存在着一定的相似度，不过VAE的生成图像是很模糊的，无法直接作为生成模型。