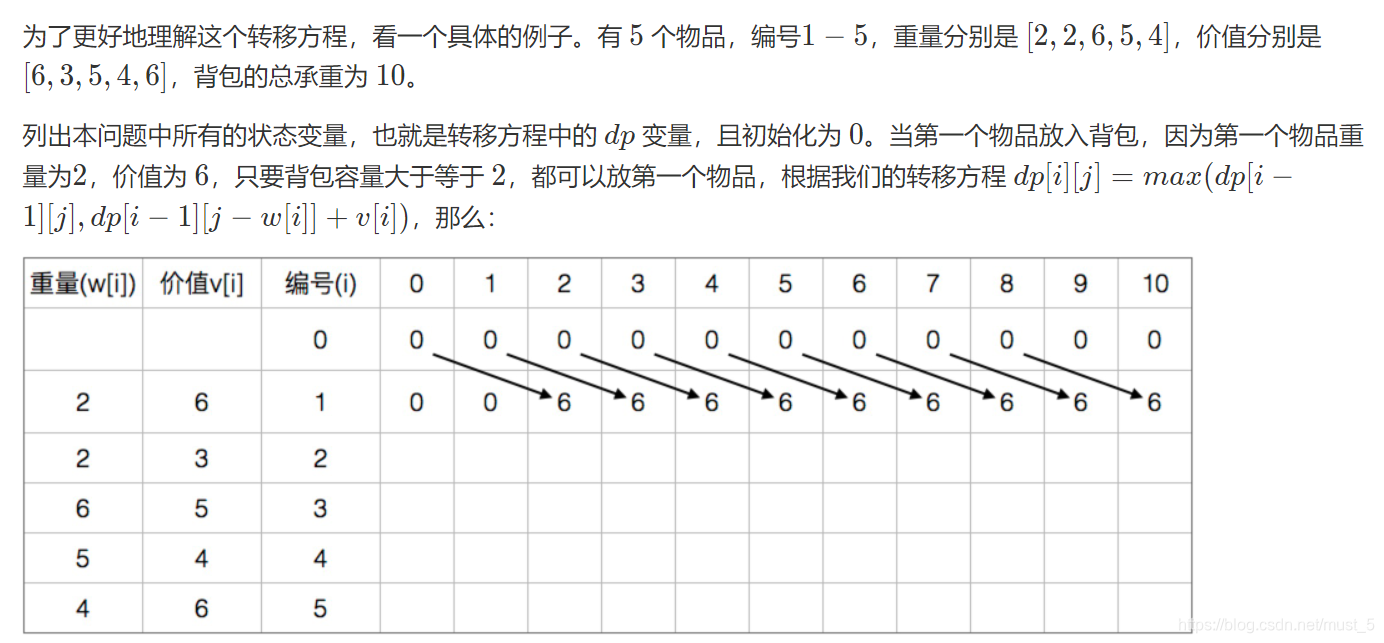
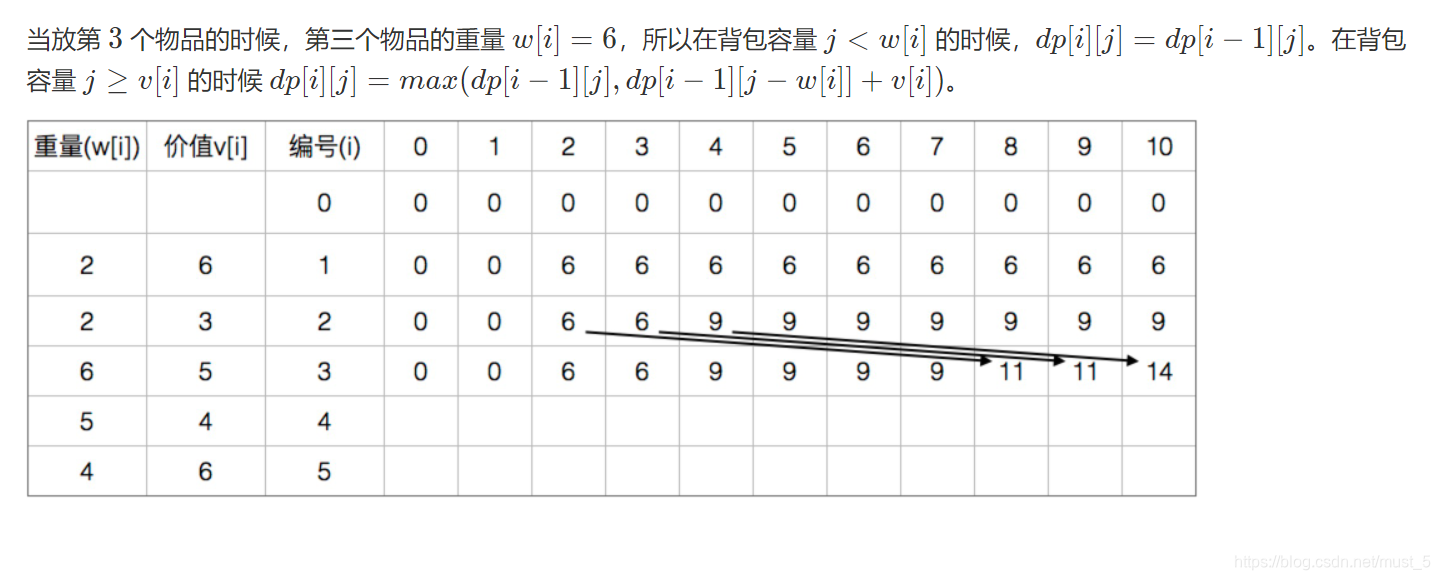
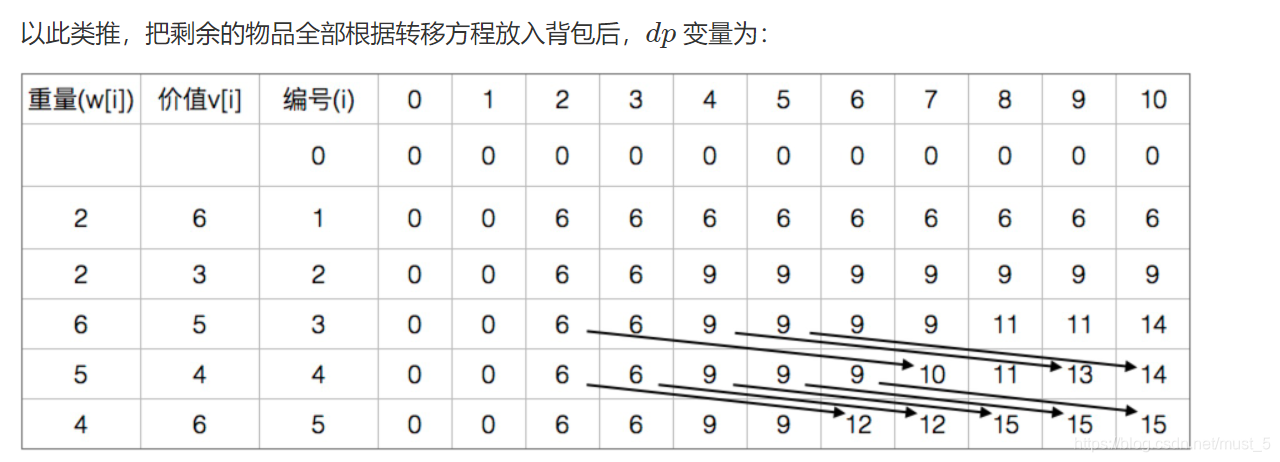
前言

dp一直是自己弱势，某些题的状态方程方程是真不好想.0.0.
而背包问题一直是dp的入门级别问题，重新整理整理吧…写写博客也算加强记忆吧

一、01背包

通过上面的表格，可以知道当这5个物品放入容量为10的背包中，最大的价值为15，即dp[5][10] = 15。

for (int i = 1; i <= N; ++i) {
    for (int j = 0; j <= V; ++j) {
        if(j >= w[i]) {
            dp[i][j] = max(dp[i - 1][j - w[i]] + v[i], dp[i - 1][j]);
        }
        else {
            dp[i][j] = dp[i-1][j];
        }
    }
}

时间上是两重循环，时间复杂度O(NV)，空间复杂度O（NV）。

除此，还可以进一步优化空寂复杂度：

for (int i = 1; i <= n; ++i)
    for (int j = v; j >= w[i]; --j)
        dp[j] = max(dp[j - w[i]] + v[i], dp[j]);

这样的空间复杂度就为O(V)了。

二、完全背包

for (int i = 1; i <= n; ++ i)
    for (int j = c[i]; j <= v; ++ j)
        dp[j] = max(dp[j - c[i]] + w[i], dp[j]);

可以发现：与01背包相比，完全背包只是第二重循环的顺序发生了改变。我们保证用较小容量的最大价值去更新较大容量的最大价值，不重不漏。时间复杂度O(VN)，空间复杂度O(V)。

三、多重背包

多重背包问题限定了一种物品的个数，解决多重背包问题，也可以把它转化为0-1背包问题。

看代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int N,V;
int w[100],v[100],num[100];
int f[100][100];

int MultiKnapsack()
{
	int nCount = 0;
	memset(f,0,sizeof(f));
	for (int i = 1;i <= N;i++)
	{
		for (int j = w[i];j <= V;j++)
		{
			nCount = min(num[i],j/w[i]);
			for (int k = 0;k <= nCount;k++)
			{
				f[i][j] = max(f[i][j],f[i - 1][j - k * w[i]] + k * v[i]);
			}
		}
	}
	return f[N][V];
}
int main()
{

	cin>>N>>V;
	for(int i=1;i<=N;i++) cin>>w[i];
	for(int i=1;i<=N;i++) cin>>v[i];
	for(int i=1;i<=N;i++) cin>>num[i];
	cout<<MultiKnapsack()<<endl;

	return 1;
}
/*
input:
3 8
1 2 2
6 10 20
10 5 2
output:
64
*/


#include <iostream>
#include <cstring>
using namespace std;

 int N ;//物品个数
 int W;//背包容量
int Weight[110];
int Value[110] ;
int Num[110];

int f[110] ;///用f[j]表示，第i次循环后，f[j]中存储的前i件物品放入容量为j的背包可获得的最大价值

void ZeroOnePack(int nWeight,int nValue)
{
	for (int j = W;j >= nWeight;j--)
	{
		f[j] = max(f[j],f[j - nWeight] + nValue);
	}
}


void CompletePack(int nWeight,int nValue)
{
	for (int j = nWeight;j <= W;j++)
	{
		f[j] = max(f[j],f[j - nWeight] + nValue);
	}
}

int MultiKnapsack()
{
    memset(f,0,sizeof(f));
	int k = 1;
	int nCount = 0;
	for (int i = 1;i <= N;i++)
	{
		if (Weight[i] * Num[i] >= W)
		{
			CompletePack(Weight[i],Value[i]);
		}
		else
		{
			k = 1;
			nCount = Num[i];
			while(k <= nCount)
			{
				ZeroOnePack(k * Weight[i],k * Value[i]);
				nCount -= k;
				k *= 2;
			}
			ZeroOnePack(nCount * Weight[i],nCount * Value[i]);
		}
	}
	return f[W];
}

int main()
{
    cin>>N>>W;
	for(int i=1;i<=N;i++) cin>>Weight[i];
	for(int i=1;i<=N;i++) cin>>Value[i];
	for(int i=1;i<=N;i++) cin>>Num[i];
	cout<<MultiKnapsack()<<endl;

	return 1;
}