文章转于 伯禹学习平台-动手学强化学习 （强推）
本文所有代码均可在jupyter notebook运行
与君共勉，一起学习。
更多Ai资讯：公主号AiCharm

1. 简介

  在之前的内容中，我们学习了基于值函数的方法（DQN）和基于策略的方法（REINFORCE），其中基于值函数的方法只学习一个价值函数，而基于策略的方法只学习一个策略函数。那么一个很自然的问题，有没有什么方法既学习价值函数，又学习策略函数呢？答案就是 Actor-Critic。Actor-Critic 是一系列算法，目前前沿的很多高效算法都属于 Actor-Critic 算法，今天我们将会介绍一种最简单的 Actor-Critic 算法。需要明确的是，Actor-Critic 算法本质上是基于策略的算法，因为这系列算法都是去优化一个带参数的策略，只是其中会额外学习价值函数来帮助策略函数的学习。

2. Actor-Critic 算法

  我们回顾一下在 REINFORCE 算法中，目标函数的梯度中有一项轨迹回报，来指导策略的更新。而值函数的概念正是基于期望回报，我们能不能考虑拟合一个值函数来指导策略进行学习呢？这正是 Actor-Critic 算法所做的。让我们先回顾一下策略梯度的形式，在策略梯度中，我们可以把梯度写成下面这个形式：
$$g=\mathbb{E}\left[\sum _{t=0}^{\infty }{\psi }_t{\nabla }_{\theta }\log {\pi }_{\theta }\left(a_t\mid s_t\right)\right]$$
其中 ${\psi }_t$ 可以有很多种形式:

1. ${\sum }_{t=0}^{\infty }{\gamma }^t{r}_{t^{\prime }}$ : 轨迹的总回报 $\quad
2. ${\sum }_{t^{\prime }=t}^{\infty }{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}$ : 动作 $a_t$ 之后的回报
3. ${\sum }_{t^{\prime }=t}^{\infty }{r}_{t^{\prime }}-b\left(s_t\right)$ : 基准线版本的改进
4. $Q^{{\pi }_{\theta }}\left(s_t,a_t\right):$ 动作价值函数
5. $ \cdot A^{\pi_{\theta}}\left(s_{t}, a_{t}\right)😒 优势函数
6. $r_t+\gamma V^{{\pi }_{\theta }}\left(s_{t+1}\right)-V^{{\pi }_{\theta }}\left(s_t\right)$ : 时序差分残差

  在 REINFORCE 的最后部分，我们提到了 REINFORCE通过蒙特卡洛采样的方法对梯度的估计是无偏的，但是方差非常大，我们可以用第三种形式引入基线 (baseline) $b(s_t$ ) 来减小方差。此外我们也可以采用 Actor-Critic 算法，估计 一个动作价值函数 $Q$ 来代替蒙特卡洛采样得到的回报，这便是第 4 种形式。这个时候，我们也可以把状态价值函数 $V作为基线，从偍牧$ 但是用神经网络进行估计的方法可以减小方差、提高鲁棒性。除此之外，REINFORCE 算法基于蒙特卡洛采样，只能在序列结束后进行更新，而 Actor-Critic 的方法则可以在每一步之后都进行更新。
我们将 Actor-Critic 分为两个部分: 分别是 Actor (策略网络) 和 Critic (价值网络)：

• Critic 要做的是通过 Actor 与环境交互收集的数据学习一个价值函数，这个价值函数会用于帮助 Actor 进行更新策略。
• Actor 要做的则是与环境交互，并利用 Ctitic 价值函数来用策略梯度学习一个更好的策略。
  $$\mathcal{L}(\omega )=\frac{1}{2}{\left(r+\gamma V_{\omega }\left(s_{t+1}\right)-V_{\omega }\left(s_t\right)\right)}^2$$

  与 DQN 中一样，我们采取类似于目标网络的方法，上式中 $r+\gamma V_{\omega }\left(s_{t+1}\right)$ 作为时序差分目标，不会产生梯度来更新价值函数。所以价值函数的梯度为
$$\nabla \ast \omega \mathcal{L}(\omega )=-(r+\gamma V\ast \omega (s\ast t+1)-V\ast \omega (s\ast t))\nabla \ast \omega V_{-}\omega \left(s_t\right)$$
然后使用梯度下降方法即可。接下来让我们总体看看 Actor-Critic 算法的流程吧!

• 初始化策略网络参数 $\theta$ ，价值网络参数 $\omega$
• 不断进行如下循环 (每个循环是一条序列) :
  。 用当前策略 ${\pi }_{\theta }$ 平样轨 迹 { s 1 , a 1 , r 1 , s 2 , a 2 , r 2 … } \left\{s_{1}, a_{1}, r_{1}, s_{2}, a_{2}, r_{2} \ldots\right\} {s1​,a1​,r1​,s2​,a2​,r2​…}
  。 为每一步数据计算: ${\delta }_t=r_t+\gamma V_{\omega }\left(s_{t+1}\right)-V_{\omega }(s)$
  。 更新价值参数 $w=w+{\alpha }_{\omega }{\sum }_t{\delta }_t{\nabla }_{\omega }{V}_{\omega }(s)$
  。 更新策略参数 $\theta =\theta +{\alpha }_{\theta }{\sum }_t{\delta }_t{\nabla }_{\theta }\log {\pi }_{\theta }(a\mid s)$

  好了！这就是 Actor-Critic 算法的流程啦，让我们来用代码实现它看看效果如何吧!

3. Actor-Critic 代码实践

  我们仍然在 Cartpole 环境上进行 Actor-Critic 算法的实验。

import gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import rl_utils

  定义我们的策略网络 PolicyNet，与 REINFORCE 算法中一样。

class PolicyNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(PolicyNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return  F.softmax(self.fc2(x),dim=1)

  Actor-Critic 算法中额外引入一个价值网络，接下来的代码定义我们的价值网络 ValueNet，输入是状态，输出状态的价值。

class ValueNet(torch.nn.Module):
    def __init__(self, state_dim, hidden_dim):
        super(ValueNet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, 1)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        return self.fc2(x)

  再定义我们的 ActorCritic 算法。主要包含采取动作和更新网络参数两个函数。

class ActorCritic:
    def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr, gamma, device):
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        self.critic = ValueNet(state_dim, hidden_dim).to(device) # 价值网络
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(), lr=critic_lr) # 价值网络优化器
        self.gamma = gamma

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float)
        probs = self.actor(state)
        action_dist = torch.distributions.Categorical(probs)
        action = action_dist.sample()
        return action.item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'], dtype=torch.float)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1)
        rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1, 1)
        next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float)
        dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1, 1)

        td_target = rewards + self.gamma * self.critic(next_states) * (1 - dones) # 时序差分目标
        td_delta = td_target - self.critic(states) # 时序差分误差
        log_probs = torch.log(self.actor(states).gather(1, actions))
        actor_loss = torch.mean(-log_probs * td_delta.detach())
        critic_loss = torch.mean(F.mse_loss(self.critic(states), td_target.detach())) # 均方误差损失函数
        self.actor_optimizer.zero_grad()
        self.critic_optimizer.zero_grad()
        actor_loss.backward() # 计算策略网络的梯度
        critic_loss.backward() # 计算价值网络的梯度
        self.actor_optimizer.step() # 更新策略网络参数
        self.critic_optimizer.step() # 更新价值网络参数

  定义好 Actor 和 Critic，我们就可以开始实验了，看看 Actor-Critic 在 Cartpole 环境上表现如何吧！

actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")

env_name = 'CartPole-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = ActorCritic(state_dim, hidden_dim, action_dim, actor_lr, critic_lr, gamma, device)

return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
----------------------------------------------------------------------------------------------Iteration 0: 100%|██████████| 100/100 [00:00<00:00, 218.65it/s, episode=100, return=21.100]
Iteration 1: 100%|██████████| 100/100 [00:01<00:00, 95.81it/s, episode=200, return=72.800]
Iteration 2: 100%|██████████| 100/100 [00:02<00:00, 45.96it/s, episode=300, return=109.300]
Iteration 3: 100%|██████████| 100/100 [00:05<00:00, 12.55it/s, episode=400, return=163.000]
Iteration 4: 100%|██████████| 100/100 [00:08<00:00, 11.24it/s, episode=500, return=193.600]
Iteration 5: 100%|██████████| 100/100 [00:08<00:00, 11.11it/s, episode=600, return=195.900]
Iteration 6: 100%|██████████| 100/100 [00:08<00:00, 11.88it/s, episode=700, return=199.100]
Iteration 7: 100%|██████████| 100/100 [00:08<00:00, 11.77it/s, episode=800, return=186.900]
Iteration 8: 100%|██████████| 100/100 [00:08<00:00, 11.23it/s, episode=900, return=200.000]
Iteration 9: 100%|██████████| 100/100 [00:08<00:00, 11.22it/s, episode=1000, return=200.000]

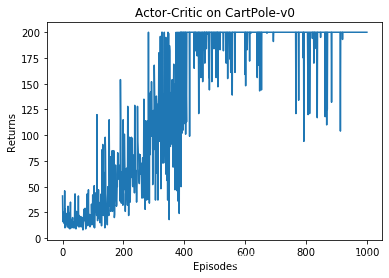
  在 CartPole-v0 环境中，满分就是 200 分，让我们来看看每个序列得分如何吧！

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list,return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()

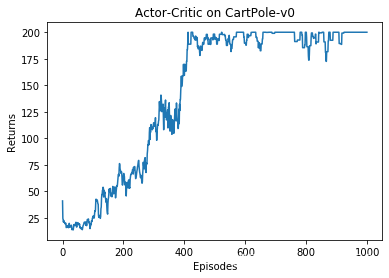
mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()

  根据实验结果我们发现，Actor-Critic 算法很快便能收敛到最优策略，并且训练过程非常稳定，抖动情况相比 REINFORCE 算法有了明显的改进，这多亏了价值函数的引入减小了方差。

4. 总结

  我们在本章中学习了 Actor-Critic 算法，它是基于策略和基于价值的方法的叠加。Actor-Critic 算法非常实用，往后像 DDPG、TRPO、PPO、SAC 这样的算法都是在 Actor-Critic 框架下进行发展的，深入了解 Actor-Critic 算法对读懂目前深度强化学习的研究热点大有裨益。
更多Ai资讯：公主号AiCharm

相关资源来自：伯禹学习平台-动手学强化学习