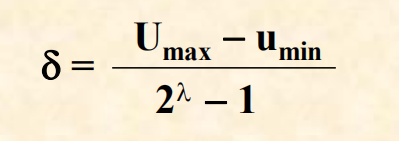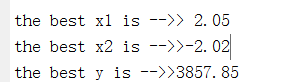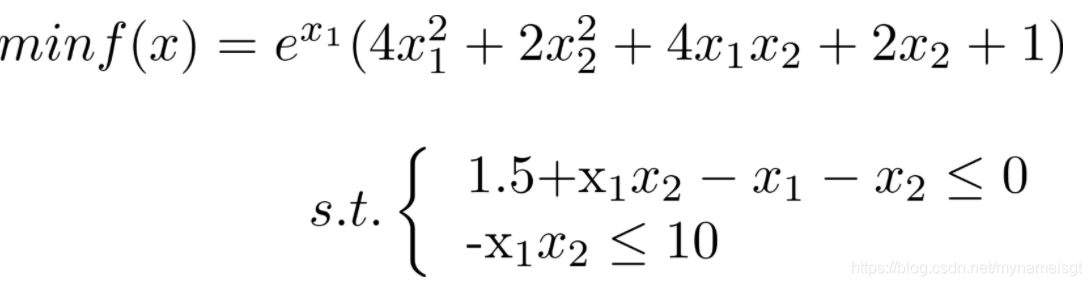现代优化算法——遗传算法(GA)
文章目录
1.遗传算法的基本介绍:
遗传算法,由达尔文进化论的自然选择和遗传传机理的生物进化构成的计算模拟模型,优胜劣汰的进化机制。自然的进化包括选择,交叉,变异等,保证了种群最优。
1.1编码与解码
(1)编码
假设某一参数的取值范围是[u_min,u_max],用长度为λ的二进制编码符号串来表示该参数,则它总共能够产生2^λ种不同的编码,参数编码时的对应关系如下:
000…000=0 u_min
000…001=1 u_min+σ
000…002=2 u_min+2σ
…
111…111=2^λ-1 u_max
其中,σ为二进制编码的编码精度,其公式为:
(2)解码
例子:
1.2个体适应度
规定,要求所有个体的适应度必须为正数或零,不能是负数。
当优化目标是求函数最大值,若目标函数总取正值,可以直接设定个体的适应度F(x)就等于相应的目标函数值f(x),即:F(x)=f(x)
当优化目标是求函数最小值,若目标函数总取负值,只需对其增加一个符号就可将其转化位求目标函数的最大值的优化问题,即:
F(x)=-f(x),那么minf(x)=max(-f(x))
然而在实际优化问题中的目标函数值有正也有负,优化目标有求函数最大值,也有求函数最小值,显然上面两式保证不了所有情况下个体的适应度都是非负数这个要求。
一般采用下面*两种方法之一将目标函数值f(x)变换为个体的适应度F(x):
1.3进化机制
1.3.1比例选择算子
(1)选择算子或复制算子的作用:
从当前代群体中选择出一些比较优良的个体,并将其复制到下一代群体中。
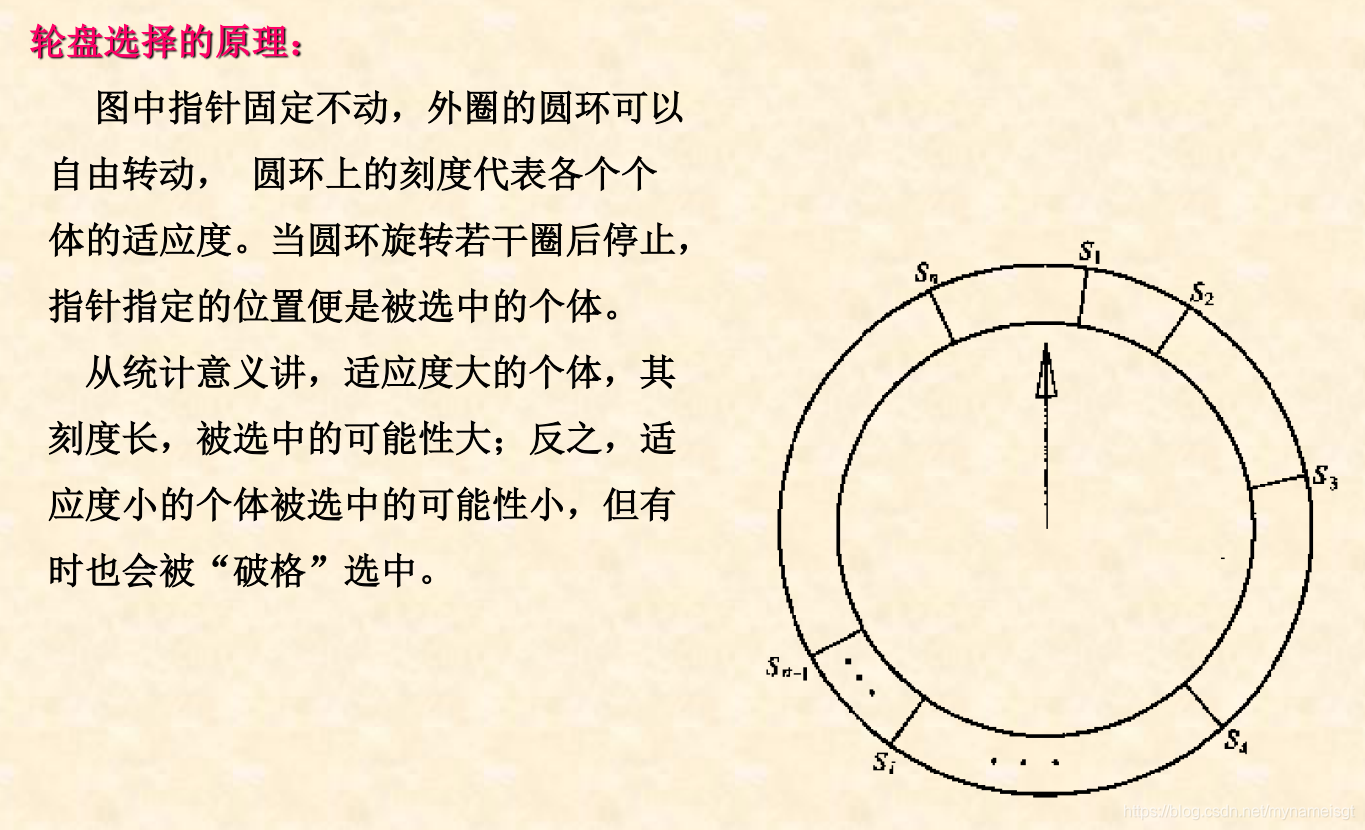
(2)最常用和最基本的选择算子:比例选择算子。
(3)个体被选中并遗传到下一代群体中的概率与该个体的适应度大小成正比。
(4)轮盘法的基本精神是:个体被选中的概率取决于个体的相对适应度:
1.3.2单点交叉算子
1.对群体中的个体进行两两随机配对。
若群体大小为M,则共有 [ M/2 ]对相互配对的个体组。
2.每一对相互配对的个体,随机设置某一基因座之后的位置为交叉点。 若染色体的长度为λ,则共有(λ-1)个可能的交叉点位置。
3.对每一对相互配对的个体,依设定的交叉概率p在其交叉点处相互交换两个个体的部分染色体,从而产生出两个新的个体。(交叉概率一般取为0.4~0.99)
1.3.3变异算子
基本变异算子是最简单和最基本的变异操作算子。
对于基本遗传算法中用二进制编码符号串所表示的个体,若需要进行变异操作的某一基因座上的原有基因值为0,则变异操作将该基因值变为1,反之,若原有基因值为1,则变异操作将其变为0.
基本位变异因子的具体执行过程:
1.对个体的每一个基因座,依变异概率p指定其为变异点。(变异概率一般取为0.00001~0.1)
2.对每一个指定的变异点,对其基因值做取反运算或用其它等位基因来代替,从而产生出一个新的个体。
2.例题讲解
2.1例题1
1、编码与解码,使用长度为10位的二进制编码串来分别表示x1,x2,此时的精度σ=4.096/1023。将两个变量放入一串编码中,该串编码长度为20(前十位代表x1,后10位代表x2)
2 、适应度函数:f(x1,x2)恒大于0,可直接作为适应度函数。
3、比例选择、交换、变异算子。
GAmain.m(主函数)
function GAmain()
clear;
clc;
%种群大小
popsize = 90;
%二进制编码长度
chromelength = 20;
%交叉概率
pc = 0.7;
%变异概率
pm = 0.01;
%初始种群 %pop = population 种群
pop = initpop(popsize, chromelength);
%迭代100次
for i = 1:100
%计算适应度值?
objvalue = cal_objvalue(pop);
fitvalue = objvalue;
%选择复制
newpop = selection(pop, fitvalue);
%交换
newpop = crossover(newpop, pc);
%变异
newpop = mutation(newpop, pm);
%更新种群
pop = newpop;
%寻找最优解并打印在command窗口
[bestindividual, bestfit] = best(pop, fitvalue);
[x1b, x2b] = binary2decimal(bestindividual);
fprintf('the best x1 is -->>%5.2f\n', x1b);
fprintf('the best x2 is -->>%5.2f\n', x2b);
fprintf('the best y is -->>%5.2f\n', bestfit);
%更新后的种群
[x1, x2] = binary2decimal(newpop);
y = cal_objvalue(newpop);
end
fprintf('------------------------------------------f\n');
fprintf('the best x1 is -->>%5.2f\n', x1b);
fprintf('the best x2 is -->>%5.2f\n', x2b);
fprintf('the best y is -->>%5.2f\n', bestfit);
figure; %%绘出最优解所在位置
x3 = -2.048:0.01:2.048;
x4 = -2.048:0.01:2.048;
[x5, x6] = meshgrid(x3, x4);
y1 = (1 - x5).^2 + 100*(x6 - x5.^2).^2;
mesh(x5, x6, y1);
hold on;
plot3(x1b, x2b, bestfit, '*');
initpop.m(初始化种群函数)
%初始化种群
function pop = initpop(popsize, chromelength)
%随机产生90*20的0 1序列作为初始化种群
pop = round(rand(popsize, chromelength));
binary2decimal.m(二进制转化为十进制函数)
%二进制转化为十进制
function [pop3 pop4] = binary2decimal(pop)
[px, py] = size(pop);
%计算x1的数值矩阵
for i = 1:py - 10 %%前10个编码代表x1
pop1(:,i) = 2.^(py - 10 - i)*pop(:,i);
end
%计算x2的数值矩阵
for i = 11:py %%后10个编码代表x2
pop2(:,i - 10) = 2.^(py - i)*pop(:,i);
end
%x1求和后的列向量
temp1 = sum(pop1, 2);
%x2求和后的列向量
temp2 = sum(pop2, 2);
%x1转换为十进制
pop3 = -2.048 + 4.096/1023*temp1;
%x2转化为十进制
pop4 = -2.048 + 4.096/1023*temp2;
cal_objvalue.m(计算适应度函数)
%计算适应度函数(也就是香蕉函数值)
function objvalue = cal_objvalue(pop)
[x1, x2] = binary2decimal(pop);
objvalue = (1 - x1).^2 + 100*(x2 - x1.^2).^2;
selection.m(选择复制函数)
%选择和复制 轮盘赌法
function [newpop] = selection(pop, fitvalue)
[px, py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
%概率求和排序
p_fitvalue = cumsum(p_fitvalue);
%产生随机概率并排序
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= px
if(ms(newin) < p_fitvalue(fitin))
newpop(newin,:) = pop(fitin,:);
newin = newin + 1;
else
fitin = fitin + 1;
end
end
crossover.m(交换函数)
%交换
function [newpop] = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
%理论是随机交换(交换哪个,和谁交换,交换哪一部分都是随机的),这里采用i和i+1的随机部分交换,尽可能达到随机
for i = 1:2:px - 1
if(rand < pc)
cpoint = round(rand*py);
newpop(i,:) = [pop(i,1:cpoint), pop(i+1, cpoint + 1:py)];
newpop(i+1, :) = [pop(i+1,1:cpoint), pop(i, cpoint+1:py)];
else
newpop(i, :) = pop(i,:);
newpop(i+1,:) = pop(i+1,:);
end
end
mutation.m(变异函数)
%变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
if(rand < pm)
mpoint = round(rand*py);
if mpoint <= 0
mpoint = 1;
end
newpop(i,:) = pop(i,:);
if newpop(i, mpoint) == 0
newpop(i, mpoint) =1;
else newpop(i, mpoint) == 1
newpop(i, mpoint) = 0;
end
else
newpop(i,:) = pop(i,:);
end
end
best.m(选择最优个体函数)
%选择最优个体
function [bestindividual bestfit] = best(pop, fitvalue)
[px, py] = size(pop);
bestfit = fitvalue(1);
bestindividual = pop(1,:);
for i = 2:px
if fitvalue(i) > bestfit
bestfit = fitvalue(i);
bestindividual = pop(i, :);
end
end
运行结果如下:
接近最大值的最优解(x1=-2.048,x2=-2.048)
2.2例题2
f(x1,x2)=x12 +x22 ;
x1∈{1,2,3,4,5};x2∈{1,2,3,4,5}
解法和第一题类似
1、编码与解码:自变量都是整数且不超过7,令每个自变量以3位二进制编码000~111∈[0,7],那么每个个体就是六位二进制数。(前三个编码代表x1,后三个编码代表x2)
2、适应度函数:f(x1,x2)恒大于0,所以可直接作为适应度函数。
3、三种算子:选择、交换、变异同第一问一样。
代码如下:
GAmain.m
function GAmain()
clear;
clc;
%种群大小
popsize = 90;
%二进制编码长度
chromelength = 6;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群 %pop = population 种群
pop = initpop(popsize, chromelength);
%迭代100次
for i = 1:100
%计算适应度值?
objvalue = cal_objvalue(pop);
fitvalue = objvalue;
%选择复制
newpop = selection(pop, fitvalue);
%交换
newpop = crossover(newpop, pc);
%变异
newpop = mutation(newpop, pm);
%更新种群
pop = newpop;
%寻找最优解并打印在command窗口
[bestindividual, bestfit] = best(pop, fitvalue);
[x1b, x2b] = binary2decimal(bestindividual);
fprintf('the best x1 is -->>%5.2f\n', x1b);
fprintf('the best x2 is -->>%5.2f\n', x2b);
fprintf('the best y is -->>%5.2f\n', bestfit);
%更新后的种群
[x1, x2] = binary2decimal(newpop);
y = cal_objvalue(newpop);
end
fprintf('-----------------------\n');
fprintf('the best x1 is -->>%5.2f\n', x1b);
fprintf('the best x2 is -->>%5.2f\n', x2b);
fprintf('the best y is -->>%5.2f\n', bestfit);
figure; %%绘出最优解所在位置
x3 = 0:0.01:7;
x4 = 0:0.01:7;
[x5, x6] = meshgrid(x3, x4);
y1 = x5.^2 + x6.^2;
mesh(x5, x6, y1);
hold on;
plot3(x1b, x2b, bestfit, '*');
initpop.m
%初始化种群
function pop = initpop(popsize, chromelength)
%随机产生90*6的0 1序列作为初始化种群
pop = round(rand(popsize, chromelength));
cal_objvalue.m
%计算适应度函数
function objvalue = cal_objvalue(pop)
[x1, x2] = binary2decimal(pop);
objvalue = x1.^2 + x2.^2;
binary2decimal.m
%二进制转化为十进制
function [pop3 pop4] = binary2decimal(pop)
[px, py] = size(pop);
%计算x1的数值矩阵
for i= 1:py - 3
pop1(:, i) = 2.^(py - 3 - i)*pop(:,i);
end
%计算x2的数值矩阵
for i = 4:py
pop2(:, i - 3) = 2.^(py - i)*pop(:, i);
end
%x1的十进制数值
pop3 = sum(pop1, 2);
%x2的十进制数值
pop4 = sum(pop2, 2);
selection.m
%选择和复制 轮盘赌法
function [newpop] = selection(pop, fitvalue)
[px, py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
%概率求和排序
p_fitvalue = cumsum(p_fitvalue);
%产生随机概率并排序
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= px
if(ms(newin) < p_fitvalue(fitin))
newpop(newin,:) = pop(fitin,:);
newin = newin + 1;
else
fitin = fitin + 1;
end
end
crossover.m
%交换
function [newpop] = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
%理论是随机交换(交换哪个,和谁交换,交换哪一部分都是随机的),这里采用i和i+1的随机部分交换,尽可能达到随机
for i = 1:2:px - 1
if(rand < pc)
cpoint = round(rand*py);
newpop(i,:) = [pop(i,1:cpoint), pop(i+1, cpoint + 1:py)];
newpop(i+1, :) = [pop(i+1,1:cpoint), pop(i, cpoint+1:py)];
else
newpop(i, :) = pop(i,:);
newpop(i+1,:) = pop(i+1,:);
end
end
mutation.m
%变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
if(rand < pm)
mpoint = round(rand*py);
if mpoint <= 0
mpoint = 1;
end
newpop(i,:) = pop(i,:);
if newpop(i, mpoint) == 0
newpop(i, mpoint) =1;
else newpop(i, mpoint) == 1
newpop(i, mpoint) = 0;
end
else
newpop(i,:) = pop(i,:);
end
end
best.m
%选择最优个体
function [bestindividual bestfit] = best(pop, fitvalue)
[px, py] = size(pop);
bestfit = fitvalue(1);
bestindividual = pop(1,:);
for i = 2:px
if fitvalue(i) > bestfit
bestfit = fitvalue(i);
bestindividual = pop(i, :);
end
end
此时已准确求得全局最优解。
2.3例题3(多约束非线性规划问题)
1、编码:自变量使用十位二进制数表示,自定义数值范围,进行区域内的最小值计算。取-10<=x1<=10,-10<=x2<=10.
2、适应度函数:这是求最小值问题,和通常的最大值不同,不能直接使用f(x)适应度函数,需要进行一定的变换(规则如下:适应度函数大于等于0,当适应度越大,对应的函数值f(x)越小)
规定f(x)<100时,F(x)=100-f(x);f(x)>=100,F(x)=0
3、三种算子:同上
代码如下:
GAmain.m
function GAmain()
clear;
clc;
%种群大小
popsize = 100;
%二进制编码长度?
chromelength = 20;
%交叉概率
pc = 0.6;
%变异概率
pm = 0.001;
%初始种群 %pop = population 种群
pop = initpop(popsize, chromelength);
%迭代100次?
for i = 1:100
%计算适应度
objvalue = cal_objvalue(pop);
fitvalue = objvalue;
%选择复制
newpop = selection(pop, fitvalue);
%交换
newpop = crossover(newpop, pc);
%变异
newpop = mutation(newpop, pm);
%更新种群
pop = newpop;
%最佳点
[bestindividual, bestfit] = best(pop, fitvalue);
[x1b, x2b] = binary2decimal(bestindividual);
fb = exp(x1b).*(4*x1b.^2 + 2*x2b.^2 + 4*x1b.*x2b + 2*x2b + 1);
%更新后的种群
[x1, x2] = binary2decimal(newpop);
y = cal_objvalue(newpop);
f = exp(x1).*(4*x1.^2 + 2*x2.^2 + 4*x1.*x2 + 2*x2 + 1);
end
fprintf('-------------------------f\n');
fprintf('the best x1 is --->>%5.2f\n', x1b);
fprintf('the best x2 is --->>%5.2f\n', x2b);
fprintf('the best f is --->>%5.2f\n', fb);
figure; %%绘制最优解对应的位置
x3 = -10:0.1:10;
x4 = -10:0.1:10;
[x5, x6] = meshgrid(x3, x4);
y1 = exp(x5).*(4*x5.^2 + 2*x6.^2 + 4*x5.*x6 + 2*x6 + 1);
mesh(x5, x6, y1);
hold on;
plot3(x1b, x2b, fb, '*');
initpop.m
%初始化种群
function pop = initpop(popsize, chromelength)
%随机产生90*20的0 1序列作为初始化种群
pop = round(rand(popsize, chromelength));
binary2decimal.m
%二进制转化为十进制
function [pop3 pop4] = binary2decimal(pop)
[px, py] = size(pop);
%计算x1的数值矩阵
for i = 1:py - 10
pop1(:,i) = 2.^(py - 10 - i)*pop(:,i);
end
%计算x2的数值矩阵
for i = 11:py
pop2(:,i - 10) = 2.^(py - i)*pop(:,i);
end
%x1求和后的列向量
temp1 = sum(pop1, 2);
%x2求和后的列向量
temp2 = sum(pop2, 2);
%x1转换位十进制
pop3 = -10 + 20/1023*temp1;
%x2转换位十进制
pop4 = -10 + 20/1023*temp2;
cal_objvalue.m
%适应度函数
function objvalue = cal_value(pop)
[px, py] = size(pop);
[x1, x2] = binary2decimal(pop);
g1 = 1.5 + x1.*x2 - x1 - x2;
g2 = - x1.*x2;
%f值
f = exp(x1).*(4*x1.^2 + 2*x2.^2 + 4*x1.*x2 + 2*x2 + 1);
for i = 1:px
%满足约束
if g1(i)<=0 && g2(i) <= 10
%适应度函数
if f(i) < 100
objvalue(i) = 100 - f(i);
else
objvalue(i) = 0;
end
else
objvalue(i) = 1;
end
end
selectio.m
%选择和复制 轮盘赌法
function [newpop] = selection(pop, fitvalue)
[px, py] = size(pop);
totalfit = sum(fitvalue);
p_fitvalue = fitvalue/totalfit;
%概率求和排序
p_fitvalue = cumsum(p_fitvalue);
%产生随机概率并排序
ms = sort(rand(px, 1));
fitin = 1;
newin = 1;
while newin <= px
if(ms(newin) < p_fitvalue(fitin))
newpop(newin,:) = pop(fitin,:);
newin = newin + 1;
else
fitin = fitin + 1;
end
end
crossover.m
%交换
function [newpop] = crossover(pop, pc)
[px, py] = size(pop);
newpop = ones(size(pop));
%理论是随机交换(交换哪个,和谁交换,交换哪一部分都是随机的),这里采用i和i+1的随机部分交换,尽可能达到随机
for i = 1:2:px - 1
if(rand < pc)
cpoint = round(rand*py);
newpop(i,:) = [pop(i,1:cpoint), pop(i+1, cpoint + 1:py)];
newpop(i+1, :) = [pop(i+1,1:cpoint), pop(i, cpoint+1:py)];
else
newpop(i, :) = pop(i,:);
newpop(i+1,:) = pop(i+1,:);
end
end
mutation.m
%变异
function [newpop] = mutation(pop, pm)
[px, py] = size(pop);
newpop = ones(size(pop));
for i = 1:px
if(rand < pm)
mpoint = round(rand*py);
if mpoint <= 0
mpoint = 1;
end
newpop(i,:) = pop(i,:);
if newpop(i, mpoint) == 0
newpop(i, mpoint) =1;
else newpop(i, mpoint) == 1
newpop(i, mpoint) = 0;
end
else
newpop(i,:) = pop(i,:);
end
end
best.m
%选择最优个体
function [bestindividual bestfit] = best(pop, fitvalue)
[px, py] = size(pop);
bestfit = fitvalue(1);
bestindividual = pop(1,:);
for i = 2:px
if fitvalue(i) > bestfit
bestfit = fitvalue(i);
bestindividual = pop(i, :);
end
end