作者：nettee        
公众号：面向大象编程

一、原题描述

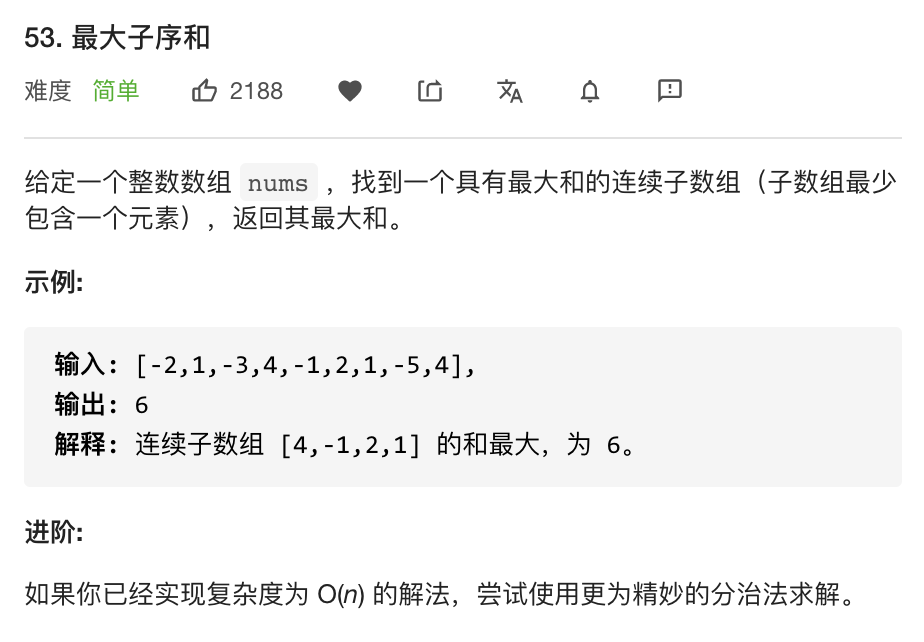
LeetCode 53. Maximum Subarray 最大子序和

二、全部解法

本文将介绍「最大子数组和」问题的以下五种解法：

其中，动态规划和贪心法其实是殊途同归，得到的是同样一份代码。分治法虽然时间复杂度不占优，却是最考验解题思路的一种方法。

本文对不同的解法都进行了时间复杂度的分析。关于时间复杂度的分析技巧可以参考文章：时间复杂度分析快速入门：题型分类法。

1. 暴力法：时间

暴力法是最容易想到的解法。我们可以直接根据题意，穷举各种可能的「子数组和」。

public int maxSubArray(int[] nums) {
    int n = nums.length;
    int res = Integer.MIN_VALUE;
    // 穷举各种可能的子数组 nums[i..j]
    for (int i = 0; i < n; i++) {
        for (int j = i; j < n; j++) {
            // 计算子数组 nums[i..j] 的和
            int sum = 0;
            for (int k = i; k <= j; k++) {
                sum += nums[k];                    
            }
            res = Math.max(res, sum);
        }
    }
    return res;
}

这个算法使用了三重循环，其中两层循环用于穷举所有可能的子数组，一层循环用于计算某个子数组的和。因此，算法的时间复杂度是 。

2. 暴力法的改进：时间

暴力法中使用的三重循环让时间复杂度变得非常大。我们可以通过一点简单的改进就能去掉一重循环，减少时间复杂度。

在上面的代码中，我们在第一层循环确定一个变量 i，然后在第二层循环依次计算 nums[i..i]、nums[i..i+1] 一直到 nums[i..n-1] 的和。我们可以直接在一个 sum 变量上依次累加，而不需要使用第三层循环进行累加。

修改后的代码如下：

public int maxSubArray(int[] nums) {
    int n = nums.length;
    int res = Integer.MIN_VALUE;
    for (int i = 0; i < n; i++) {
        int sum