1、分治算法基本思想

分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。

当我们求解某些问题时，由于这些问题要处理的数据相当多，或求解过程相当复杂，使得直接求解法在时间上相当长，或者根本无法直接求出。对于这类问题，我们往往先把它分解成几个子问题，找到求出这几个子问题的解法后，再找到合适的方法，把它们组合成求整个问题的解法。如果这些子问题还较大，难以解决，可以再把它们分成几个更小的子问题，以此类推，直至可以直接求出解为止。这就是分治策略的基本思想。

2、题目

在给定的一个序列中，找到和值最大的子序列。
分治法求解
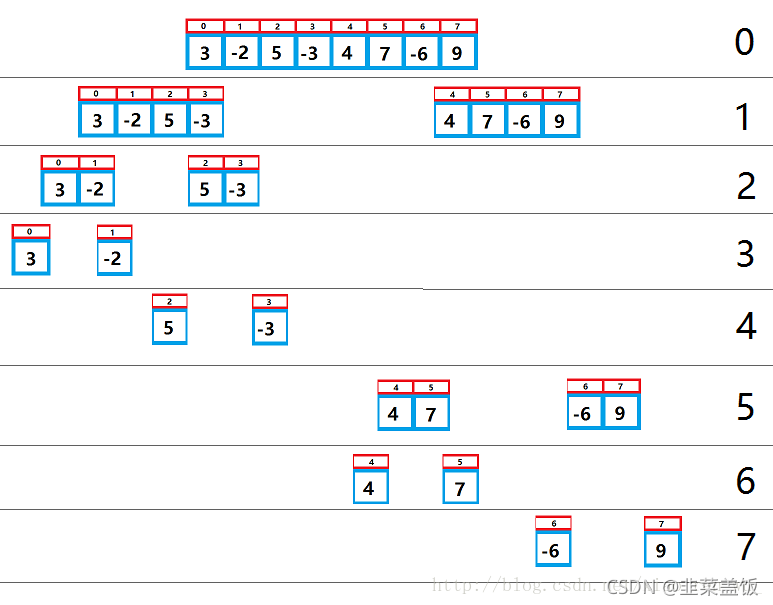
将一个大问题拆分为若干个小问题

红色框中的为元素的数组下标，对应的蓝色框为数组的值。
分割的思想跟二叉树的遍历大同小异，能左分，不右分，分到当前序列中只有一个值时，改值作为最大的序列和返回。
代码

int getMaxNum(int a,int b,int c){
    if (a > b&&a > c){
        return a;
    }
    if (b > a&&b > c){
        return b;
    }
    return c;
}
int maxSumRec(int data[], int left, int right){
    if (right - left == 1){
        //如果当前序列只有一个元素
        return data[left];
    }
    int center = (left + right) / 2;//计算当前序列的分裂点
    int maxLeftSum = maxSumRec(data,left,center);
    int maxRightSum = maxSumRec(data,center,right);
    //计算左边界最大子序列和
    int leftBonderSum = 0;
    int maxLeftBonderSum = data[center-1];
    for (int i = center - 1; i >= left; i--){
        leftBonderSum += data[i];
        if (maxLeftBonderSum < leftBonderSum){
            maxLeftBonderSum = leftBonderSum;
        }
    }
    //计算右边界最大子序列和
    int rightBonderSum = 0;
    int maxRightBonderSum = data[center];
    for (int i = center; i < right; i++){
        rightBonderSum += data[i];
        if (maxRightBonderSum < rightBonderSum){
            maxRightBonderSum = rightBonderSum;
        }
    }
    //返回当前序列最大子序列和
    return getMaxNum(maxLeftBonderSum + maxRightBonderSum, maxLeftSum, maxRightSum);
}

3、调用测试

int main(void){
    int data[8] = {3,-2,5,-3,4,7,-6,9};
    printf("%d",maxSumRec(data, 0, 8));
    return 0;
}