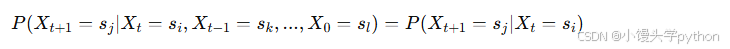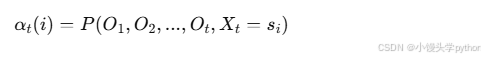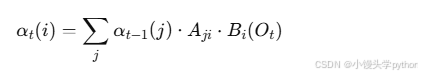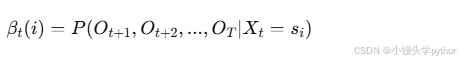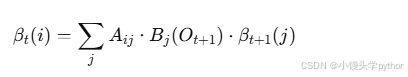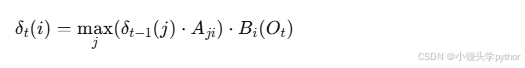【机器学习】从马尔可夫链到CRF：全方位解析序列建模的核心技术

💗💗💗欢迎来到我的博客，你将找到有关如何使用技术解决问题的文章，也会找到某个技术的学习路线。无论你是何种职业，我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章，也欢迎在文章下方留下你的评论和反馈。我期待着与你分享知识、互相学习和建立一个积极的社区。谢谢你的光临，让我们一起踏上这个知识之旅！

文章目录

🍋马尔可夫链
- 🍋定义
- 🍋示例代码
🍋隐马尔可夫模型（HMM）
- 🍋定义
- 🍋HMM的关键问题
🍋前向-后向算法
🍋维特比算法
- 🍋维特比算法递推公式
- 🍋维特比算法示例代码
🍋条件随机场模型（CRF）
🍋总结
🍋参考文献

🍋马尔可夫链

🍋定义

马尔可夫链（Markov Chain）是一种随机过程，其中系统的未来状态仅与当前状态有关，且与过去的状态无关。该性质称为马尔可夫性质。马尔可夫链可以通过转移概率矩阵来表示。
对于一个离散时间的马尔可夫链，状态空间为 S={s1,s2,s3,…,sN}，状态之间的转移满足：
在这里插入图片描述
这表明，未来的状态仅与当前状态有关，而与历史状态无关。

🍋示例代码

import numpy as np

# 定义转移概率矩阵
transition_matrix = np.array([
    [0.7, 0.3],
    [0.4, 0.6]
])

# 初始化状态
state = 0  # 假设从状态0开始

# 进行10次状态转移
for i in range(10):
    state = np.random.choice([0, 1], p=transition_matrix[state])
    print(f"Step {i+1}: State {state}")

🍋隐马尔可夫模型（HMM）

🍋定义

隐马尔可夫模型是对马尔可夫链的扩展。在HMM中，观察到的事件（即观测序列）是由一个隐藏的状态序列生成的。每个隐藏状态具有一个概率分布，用于生成观测值。

HMM的组成部分：

状态空间：假设有 N 个隐含状态S={s1,s2,s3,…,sN}
转移概率矩阵：描述隐状态之间转移的概率。
观测符号集：假设M个观测符号O={o1,o2,o3,…,oM}
发射概率矩阵：描述在给定隐状态下，观测到某个符号的概率。

🍋HMM的关键问题

给定模型和观测序列，计算隐状态序列的最优概率（如维特比算法）。
给定观测序列，估计最可能的隐状态序列（如前向-后向算法）。
模型参数估计，即从观测数据中学习HMM的参数（如Baum-Welch算法）。

🍋前向-后向算法

前向-后向算法用于给定观测序列的情况下，计算每个时间点上隐状态的后验概率。这个算法是动态规划算法，它分为两个部分：

前向算法：计算到某一时刻，给定观测序列的条件下，系统处于某一状态的概率。
后向算法：计算从某一时刻开始，给定观测序列的条件下，系统进入某一状态的概率。

🍋前向算法公式

前向概率 𝛼𝑡(𝑖)表示在时刻 t 处于状态 i 的条件下，已知观测序列O1,O2,O3,…,Ot的概率
在这里插入图片描述
递推公式：

其中，Aji是从状态j转移到状态i的概率，Bi(Ot)是在状态i下观察到Ot的概率

🍋后向算法公式

后向概率 𝛽𝑡(𝑖)表示在时刻t处于状态i是条件下，已知从t+1到T的观测序列的概率：
在这里插入图片描述
递推公式：

🍋前向-后向算法代码

import numpy as np

# 假设有2个状态，3个观测符号
A = np.array([[0.7, 0.3], [0.4, 0.6]])  # 状态转移矩阵
B = np.array([[0.5, 0.2, 0.3], [0.1, 0.4, 0.5]])  # 发射矩阵
pi = np.array([0.6, 0.4])  # 初始状态概率

# 观测序列 O = [O1, O2, O3]
O = [0, 1, 2]  # 对应的观测符号索引

# 前向算法
def forward(A, B, pi, O):
    N = A.shape[0]
    T = len(O)
    alpha = np.zeros((T, N))
    
    # 初始化
    for i in range(N):
        alpha[0, i] = pi[i] * B[i, O[0]]
    
    # 递推
    for t in range(1, T):
        for i in range(N):
            alpha[t, i] = np.sum(alpha[t-1] * A[:, i]) * B[i, O[t]]
    
    return alpha

# 计算前向概率
alpha = forward(A, B, pi, O)
print("前向概率：", alpha)

结果：
前向概率： [[0.3 0.04 ]
[0.0452 0.0456 ]
[0.014964 0.02046 ]]

🍋维特比算法

维特比算法用于在给定观测序列的情况下，找到最可能的隐状态序列。它使用动态规划方法，通过递推来计算给定观测序列的最优状态序列

🍋维特比算法递推公式

维特比算法的核心是计算每个时间点在每个隐状态下的最优路径概率
在这里插入图片描述

🍋维特比算法示例代码

def viterbi(A, B, pi, O):
    N = A.shape[0]
    T = len(O)
    
    # 初始化
    delta = np.zeros((T, N))
    psi = np.zeros((T, N), dtype=int)
    
    for i in range(N):
        delta[0, i] = pi[i] * B[i, O[0]]
    
    # 递推
    for t in range(1, T):
        for i in range(N):
            delta[t, i] = np.max(delta[t-1] * A[:, i]) * B[i, O[t]]
            psi[t, i] = np.argmax(delta[t-1] * A[:, i])
    
    # 回溯
    state_sequence = np.zeros(T, dtype=int)
    state_sequence[T-1] = np.argmax(delta[T-1])
    
    for t in range(T-2, -1, -1):
        state_sequence[t] = psi[t+1, state_sequence[t+1]]
    
    return state_sequence

# 计算最优状态序列
state_sequence = viterbi(A, B, pi, O)
print("最优状态序列：", state_sequence)

结果：
最优状态序列： [0 1 1]

🍋条件随机场模型（CRF）

条件随机场（Conditional Random Field, CRF）是一种判别式的概率模型，用于标注和分割序列数据。与隐马尔可夫模型不同，CRF直接建模条件概率 P(Y∣X)，而不是联合概率。它常用于自然语言处理和序列标注任务中。
CRF模型的特点

CRF是一个图模型，其中节点表示随机变量，边表示变量之间的依赖关系。
CRF建模的是给定输入序列 X 下输出序列 Y 的条件概率。
它采用全局的条件概率建模，避免了HMM中隐状态的独立性假设。

🍋总结

隐马尔可夫模型（HMM）和条件随机场（CRF）是两种常用于序列数据建模的统计方法。HMM假设隐状态序列和观测序列之间通过概率模型进行关联，而CRF则直接建模条件概率，避免了HMM中的独立性假设。

在实际应用中，HMM被广泛用于语音识别、自然语言处理等领域，而CRF则常用于序列标注和分割任务，如命名实体识别、词性标注等。掌握这些模型和算法对于处理复杂的序列数据非常有帮助。

🍋参考文献

关于马尔可夫模型（Markov Models），有很多经典的学术论文和书籍，它们涵盖了从基础理论到各种应用领域的不同层面。以下是一些有影响力的论文和资源，它们涉及马尔可夫链、隐马尔可夫模型（HMM）以及其他相关领域：

Markov Chains and Mixing Times
作者：David A. Levin, Yuval Peres, Elizabeth L. Wilmer
简介：这本书详细讨论了马尔可夫链的理论，特别是马尔可夫链的混合时间问题。它包括了关于状态空间、转移概率、混合过程等深入的数学分析。
链接：Markov Chains and Mixing Times
A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition
作者：Lawrence R. Rabiner
发表时间：1989年
简介：这是关于隐马尔可夫模型的经典教程，详细介绍了HMM的基本原理、算法（如前向-后向算法、维特比算法）以及它们在语音识别中的应用。它被认为是该领域的开创性工作之一，至今仍被广泛引用。
链接：A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition
Hidden Markov Models: Applications to Speech Recognition
作者：L.R. Rabiner
发表时间：1990年
简介：这篇论文进一步探讨了隐马尔可夫模型在语音识别中的应用。虽然其重点是语音领域，但它提供的数学框架和算法对于任何使用HMM的应用领域都具有参考价值。
链接：Hidden Markov Models: Applications to Speech Recognition
On the Performance of the Baum-Welch Algorithm for Training Hidden Markov Models
作者：B. L. Baum, L. E. D. A. Welleck
简介：这篇论文详细探讨了Baum-Welch算法（用于HMM参数估计）的性能。该算法是HMM的核心技术之一，用于在没有标签的训练数据上学习模型的参数。
链接：Baum-Welch Algorithm Paper
Markov Chains: From Theory to Implementation and Experimentation
作者：Paul A. Gagniuc
简介：这本书提供了关于马尔可夫链的详细理论，涵盖了离散时间和连续时间马尔可夫链的各种应用。书中还包括了实践中的代码实现和实验结果，适合对马尔可夫链及其应用感兴趣的读者。
链接：Markov Chains: From Theory to Implementation and Experimentation
The Theory of Markov Processes
作者：Andrei L. Khinchin
简介：这是一本经典的关于马尔可夫过程的书，介绍了马尔可夫链及其在不同领域中的应用，涵盖了大部分基础理论，适合那些对马尔可夫过程有深入兴趣的读者。
链接：The Theory of Markov Processes (Springer)
Markov Decision Processes: Discrete Stochastic Dynamic Programming
作者：Martin L. Puterman
简介：这本书介绍了马尔可夫决策过程（MDP），这是马尔可夫过程的一个重要扩展，常用于强化学习和优化问题。它涵盖了MDP的理论基础、解法以及实际应用。
链接：Markov Decision Processes: Discrete Stochastic Dynamic Programming
The EM Algorithm and Extensions
作者：Arthur P. Dempster, Nan M. Laird, Donald B. Rubin
简介：这篇论文介绍了期望最大化（EM）算法，这是用于隐马尔可夫模型参数估计的重要算法。EM算法常与HMM一起使用，尤其是在缺失数据的情况下。
链接：The EM Algorithm and Extensions (JSTOR)
A Markov Chain Monte Carlo Approach to Estimating the Parameters of Hidden Markov Models
作者：R. G. Bhat, P. T. W. Naylor
简介：这篇论文介绍了使用马尔可夫链蒙特卡洛（MCMC）方法来估计隐马尔可夫模型的参数。这对于那些希望在HMM中引入贝叶斯推断的研究者来说是一个有价值的参考。
链接：Markov Chain Monte Carlo for HMM
Statistical Methods for Survival Data Analysis
作者：Jerald F. Lawless
简介：这本书涵盖了生存分析中的马尔可夫模型和HMM的应用，重点介绍了在医疗统计中如何使用这些模型。它适用于那些从事生存分析或时间序列建模的研究人员。
链接：Statistical Methods for Survival Data Analysis

请添加图片描述

挑战与创造都是很痛苦的，但是很充实。