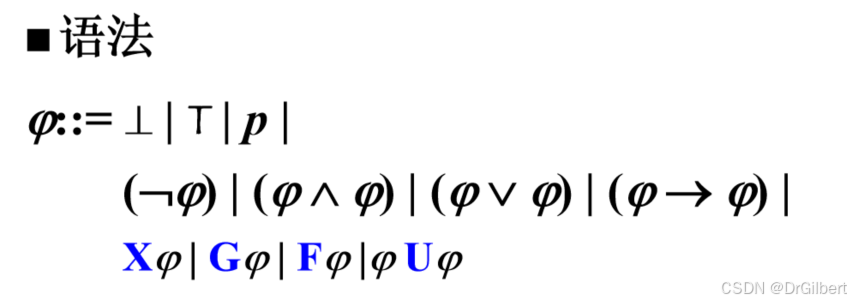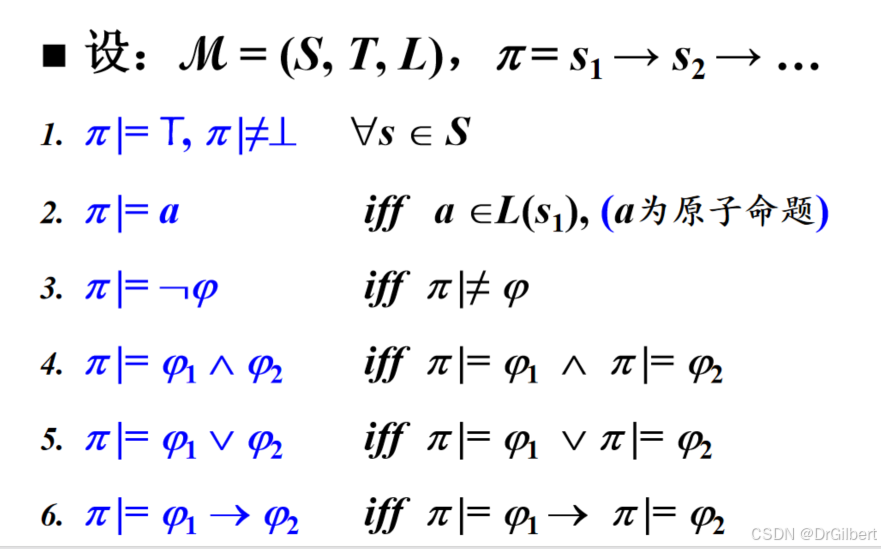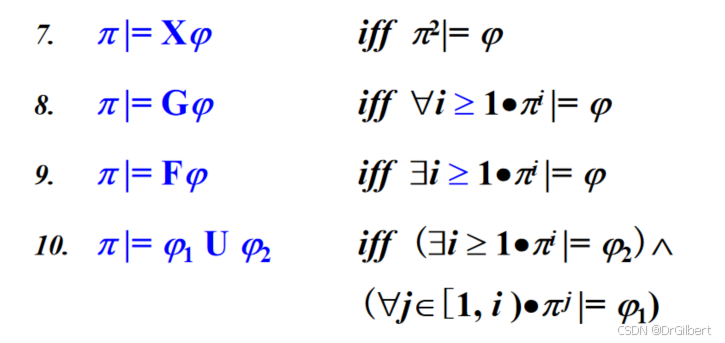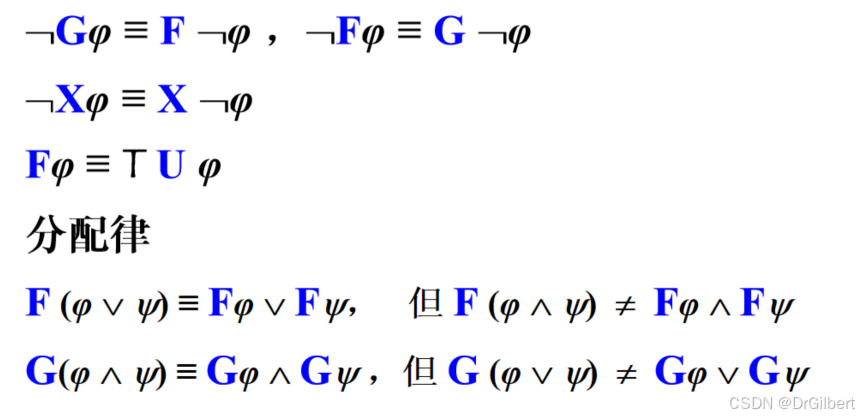文章目录
一、绪论
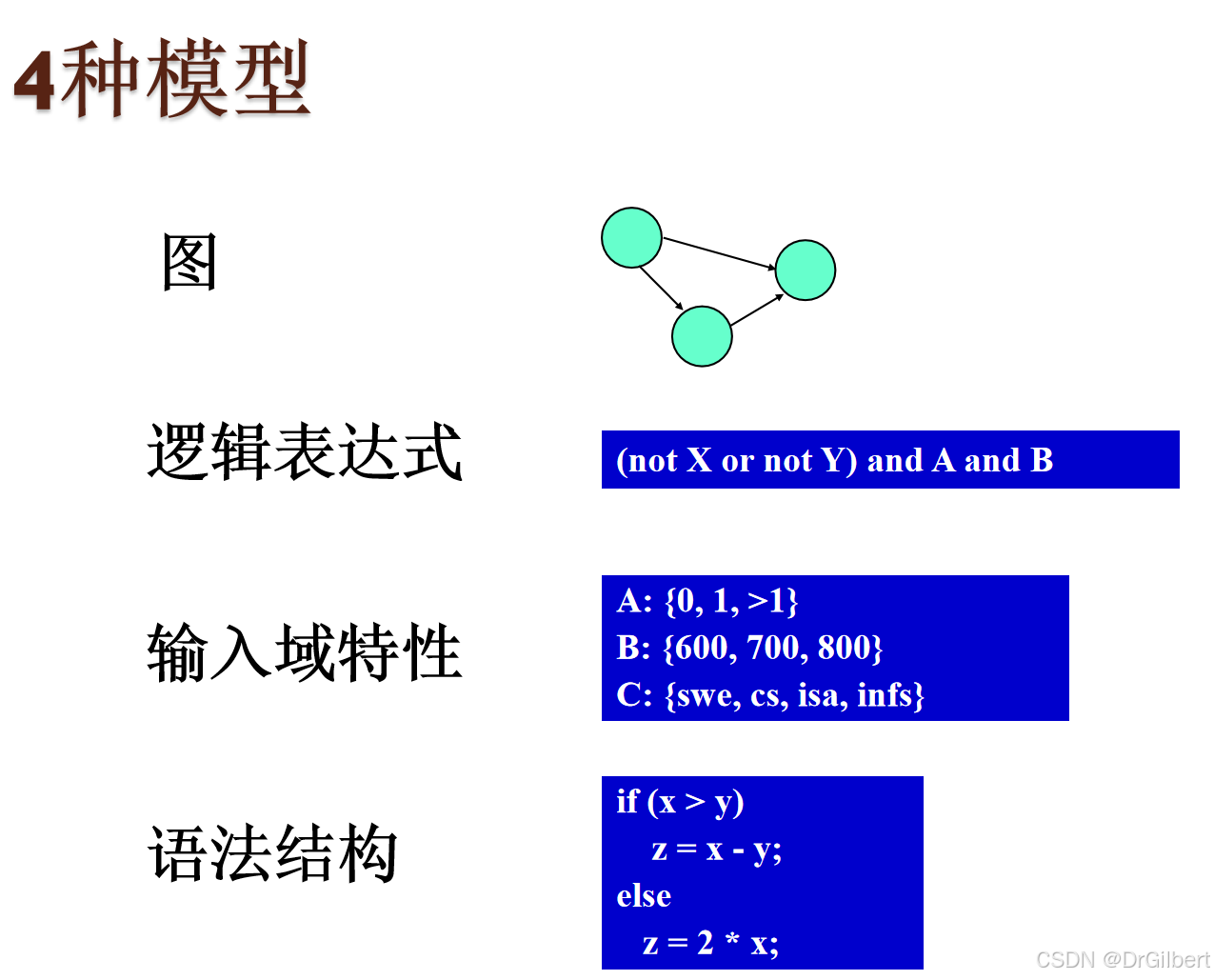
测试过程模型
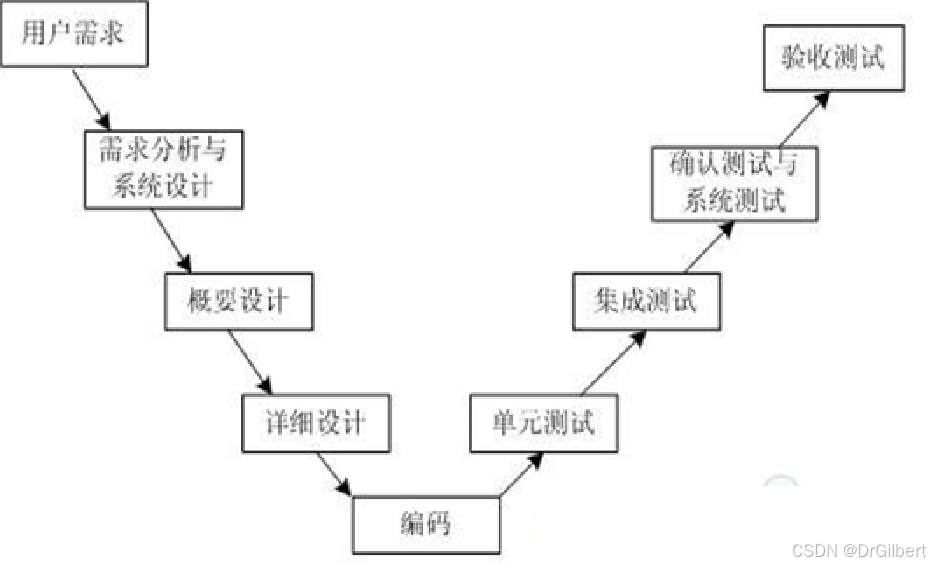
V模型:测试是编码的最后一个阶段,需求分析隐藏的问题会在最后验收才被发现。
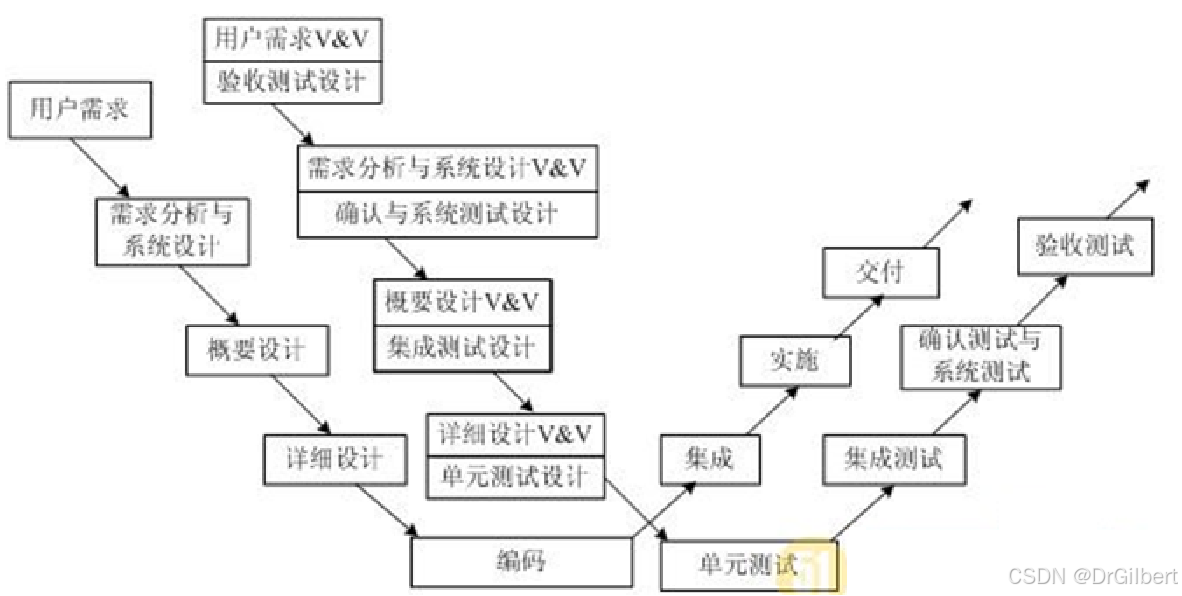
W模型:编码与测试同步进行。
软件测试技术
单元测试、集成测试、系统测试、验收测试、回归测试等(开发测试、发布测试、用户测试)
功能测试、性能测试、安全测试、压力测试、负载测试、容错测试等
白盒测试和黑盒测试(另一种:灰盒测试)
静态测试(静态分析,人工审核)和动态测试(运行代码)
传统测试和面向对象测试
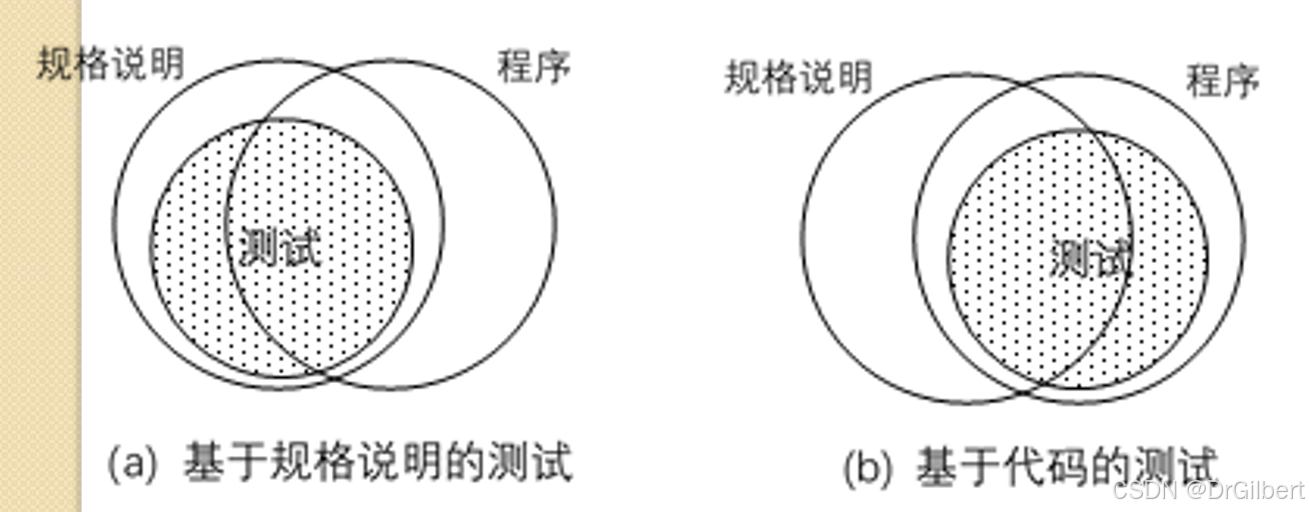
基于规格说明的测试和基于代码的测试
基于模型的测试
基于规格说明的测试和基于代码的测试
基于规格说明的测试:通过分析规格说明书,将所有可能的输入形成一个输入域。 并划分出若干个子集,从每一个子集中各挑选少量数据进行测试。(通过较少的测试用例达到尽量多的测试覆盖)
白盒测试(根据程序结构&内部逻辑设计用例)
控制流覆盖&数据流覆盖
黑盒测试(根据系统功能性规格说明设计测试用例)
等价划分&边界值分析&因果图测试&组合测试
基于模型的测试(根据模型进行测试)
基于覆盖的测试(定义一个模型然后试图覆盖它,依赖于测试准则)
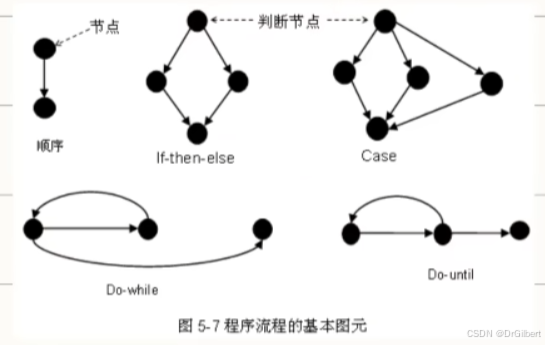
二、图覆盖
图结构覆盖(根据节点与边定义覆盖)
G
=
(
N
,
N
0
,
N
f
,
E
)
G=(N,N_0,N_f,E)
G=(N,N0,Nf,E)
N
N
N:点集合
N
0
N_0
N0:起点集合
N
f
N_f
Nf:终点集合
E
E
E:边集合
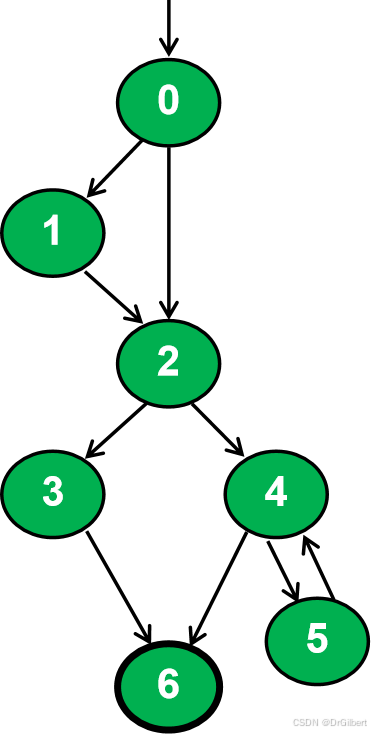
以该图为例,
N
0
=
0
N_0={0}
N0=0,
N
f
=
6
N_f={6}
Nf=6。
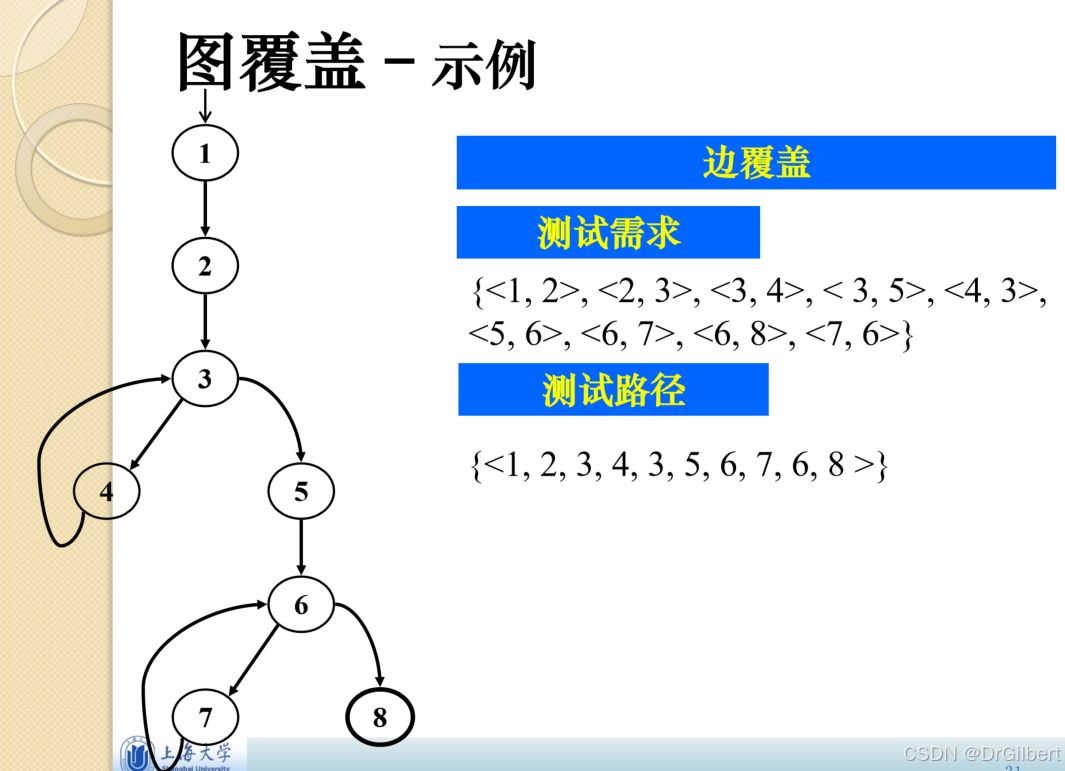
简单的结构覆盖
节点覆盖:选用尽可能少的路径数,来覆盖每个点(路径长度不超过0)。
eg:图中的测试需求(点集)为
{
0
,
1
,
2
,
3
,
4
,
5
,
6
}
\{0,1,2,3,4,5,6\}
{0,1,2,3,4,5,6}
测试路径集为<
0
,
1
,
2
,
3
,
6
0,1,2,3,6
0,1,2,3,6>,<
0
,
1
,
2
,
4
,
5
,
4
,
6
0,1,2,4,5,4,6
0,1,2,4,5,4,6>
边覆盖:选用尽可能少的路径数,来覆盖每条边(路径长度不超过1)。
eg:图中的测试需求(边集)为
{
<
0
,
1
>
,
<
0
,
2
>
,
<
1
,
2
>
,
<
2
,
3
>
,
<
2
,
4
>
,
<
3
,
6
>
,
<
4
,
5
>
,
<
4
,
6
>
,
<
5
,
4
>
}
\{<0,1>,<0,2>,<1,2>,<2,3>,<2,4>,<3,6>,<4,5>,<4,6>,<5,4>\}
{<0,1>,<0,2>,<1,2>,<2,3>,<2,4>,<3,6>,<4,5>,<4,6>,<5,4>}
测试路径集为<
0
,
1
,
2
,
3
,
6
0,1,2,3,6
0,1,2,3,6>,<0,2,4,5,4,6>
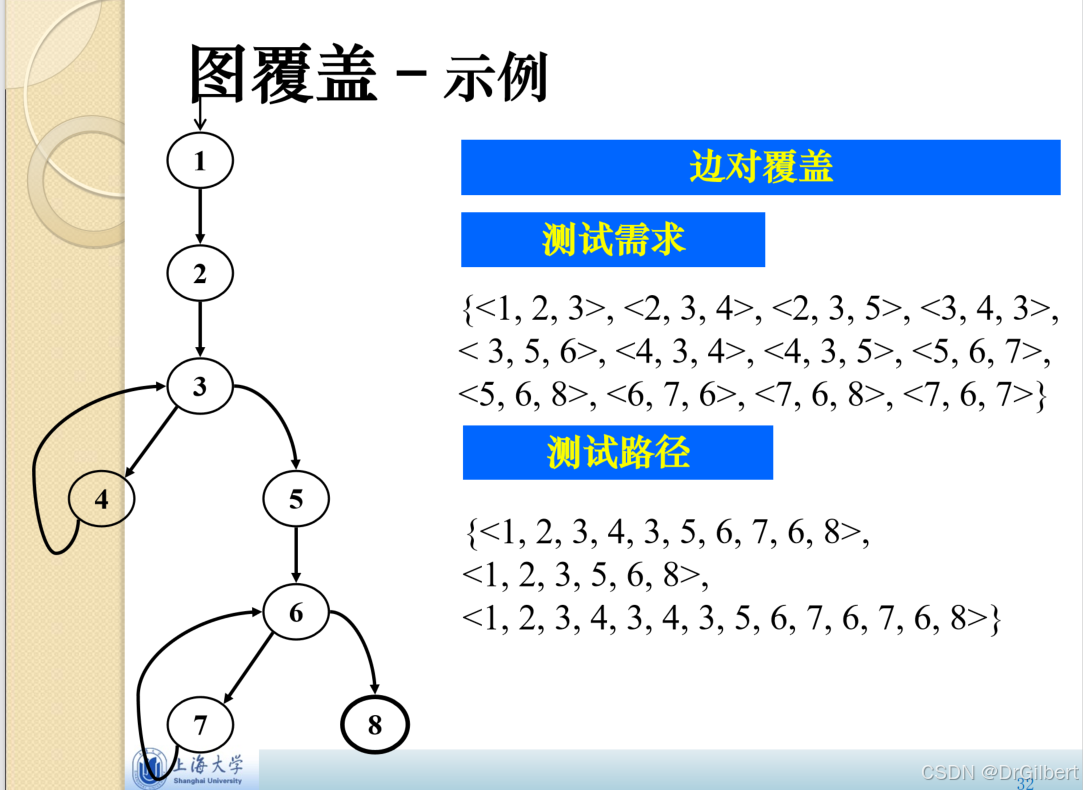
边对覆盖:选用尽可能少的路径数,来覆盖每个边对(路径长度不超过2)。
边对:<
a
,
b
,
c
a,b,c
a,b,c>表示
a
,
b
,
c
a,b,c
a,b,c三个点及其互相连接的边。
eg:图中的测试需求(边对集)为
{
<
0
,
1
,
2
>
,
<
0
,
2
,
3
>
,
<
0
,
2
,
4
>
,
<
1
,
2
,
3
>
,
<
1
,
2
,
4
>
,
<
2
,
3
,
6
>
,
<
2
,
4
,
5
>
,
<
2
,
4
,
6
>
,
<
4
,
5
,
4
>
,
<
5
,
4
,
5
>
,
<
5
,
4
,
6
>
}
\{<0,1,2>, <0,2,3>, <0,2,4>, <1,2,3>, <1,2,4>, <2,3,6>, <2,4,5>, <2,4,6>, <4,5,4>, <5,4,5>, <5,4,6>\}
{<0,1,2>,<0,2,3>,<0,2,4>,<1,2,3>,<1,2,4>,<2,3,6>,<2,4,5>,<2,4,6>,<4,5,4>,<5,4,5>,<5,4,6>}
测试路径集为
<
0
,
1
,
2
,
3
,
6
>
,
<
0
,
1
,
2
,
4
,
6
>
,
<
0
,
2
,
3
,
6
>
,
<
0
,
2
,
4
,
5
,
4
,
5
,
4
,
6
>
<0, 1, 2, 3, 6>, <0, 1, 2, 4, 6>, <0, 2, 3, 6>, <0, 2, 4, 5, 4, 5, 4, 6>
<0,1,2,3,6>,<0,1,2,4,6>,<0,2,3,6>,<0,2,4,5,4,5,4,6>
基本路径覆盖
全路径覆盖:覆盖所有可能的路径(但如果图中包含循环就难以实现)。
基本路径覆盖:覆盖图的基路径集
基路径集:一个线性独立路径集,任何一条从开始节点到终止节点的路径,都可通过基路径集中路径的线性组合而成。
线性独立路径:路径中至少包含一条其他路径不存在的边。
如何求基本路径覆盖
(1)根据程序的分支路线,绘制控制流图
(2)计算环路复杂度
V
(
G
)
V(G)
V(G)
V
(
G
)
=
E
−
N
+
2
V(G)=E-N+2
V(G)=E−N+2(边数-点数+2)
V
(
G
)
=
P
+
1
V(G)=P+1
V(G)=P+1(判定节点数+1,出度大于等于2的节点)
V
(
G
)
=
R
V(G)=R
V(G)=R(平面被图分割的区域数)
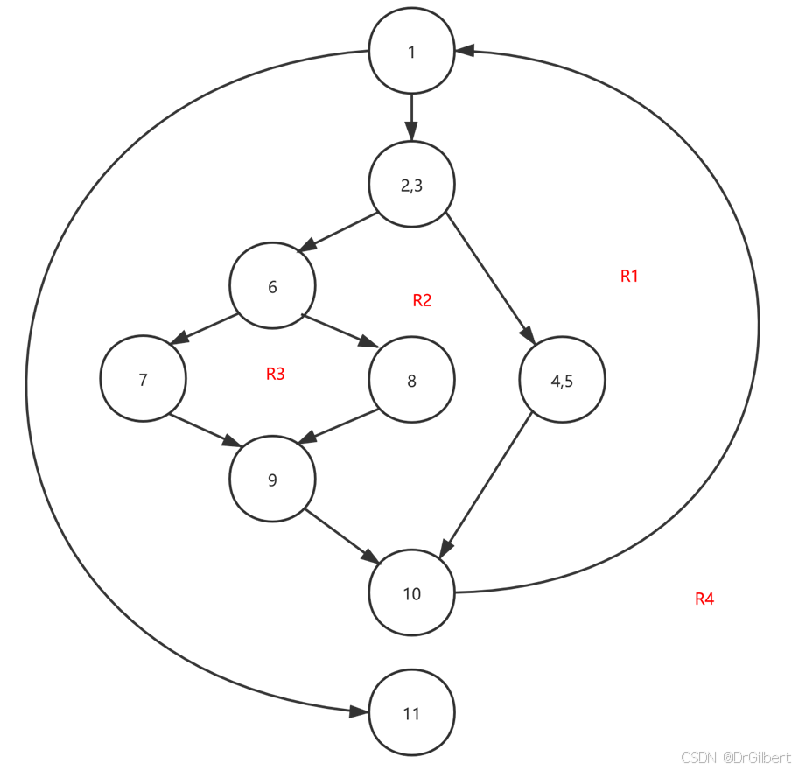
eg1:如图,
E
=
11
,
N
=
9
,
V
(
G
)
=
E
−
N
+
2
=
4
E=11,N=9,V(G)=E-N+2=4
E=11,N=9,V(G)=E−N+2=4
eg2:如图,1号、2,3号、6号是判定节点,故
V
(
G
)
=
3
+
1
=
4
V(G)=3+1=4
V(G)=3+1=4
eg3:如图,注意到平面被分割为
R
1
,
R
2
,
R
3
,
R
4
R1,R2,R3,R4
R1,R2,R3,R4四个区域,故
V
(
G
)
=
4
V(G)=4
V(G)=4
(3)根据
V
(
G
)
V(G)
V(G)确定关键路径组(
V
(
G
)
V(G)
V(G)=关键路径数!)
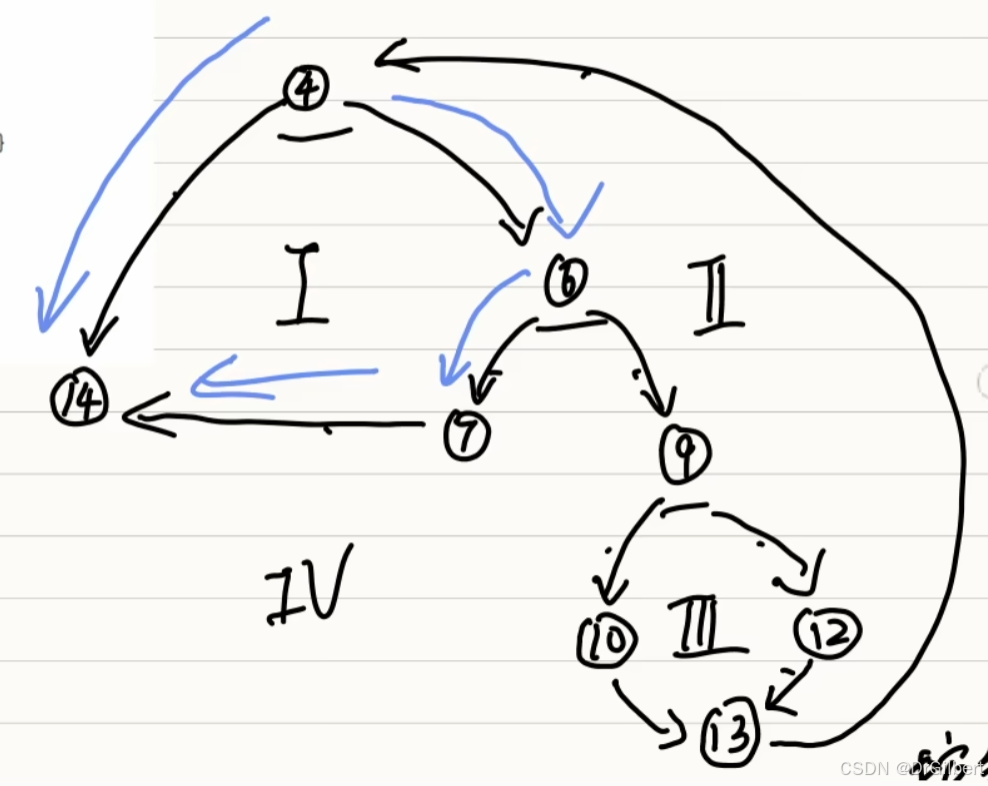
关键路径:从起点开始到终点,但每一条路径都至少一条边其他路径没有!
4
→
14
4\rightarrow 14
4→14
4
→
6
→
7
→
14
4\rightarrow 6\rightarrow 7\rightarrow 14
4→6→7→14
4
→
6
→
9
→
10
→
13
→
4
→
14
4\rightarrow 6\rightarrow 9\rightarrow 10\rightarrow 13\rightarrow 4\rightarrow 14
4→6→9→10→13→4→14
4
→
6
→
9
→
12
→
13
→
4
→
14
4\rightarrow 6\rightarrow 9\rightarrow 12\rightarrow 13\rightarrow 4\rightarrow 14
4→6→9→12→13→4→14
(4)根据关键路径编写测试用例
(存在路径说明语法可达,不存在说明语义不达)
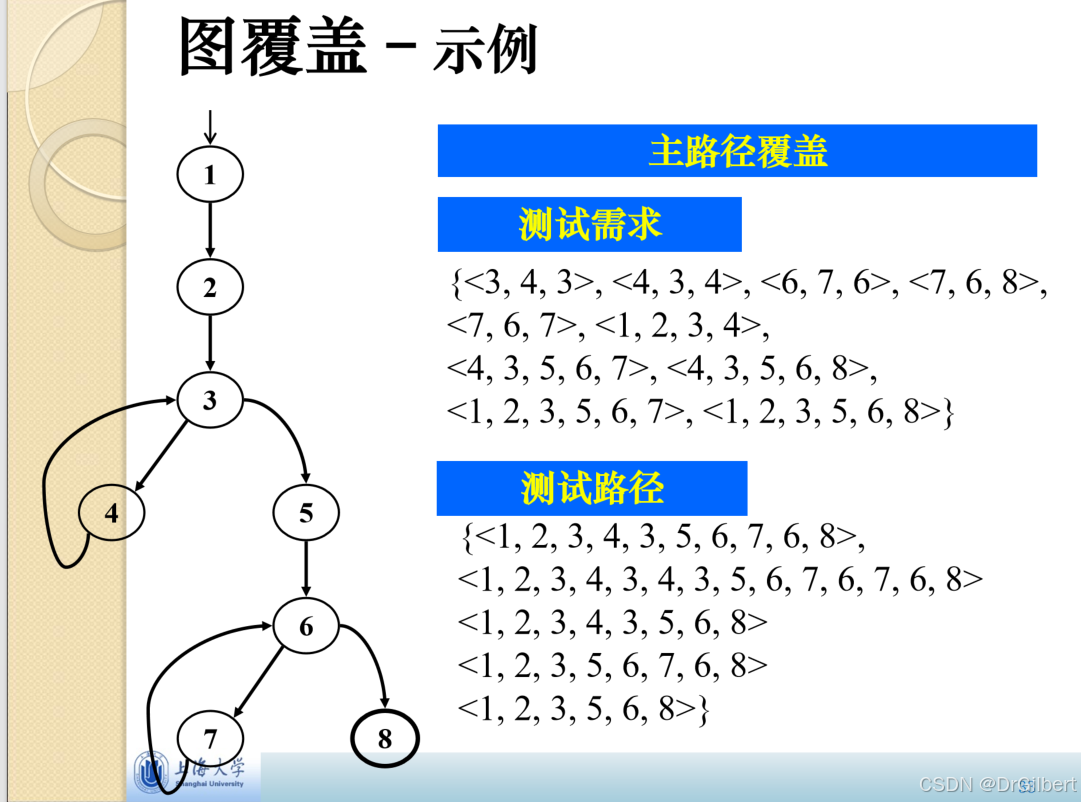
主路径覆盖
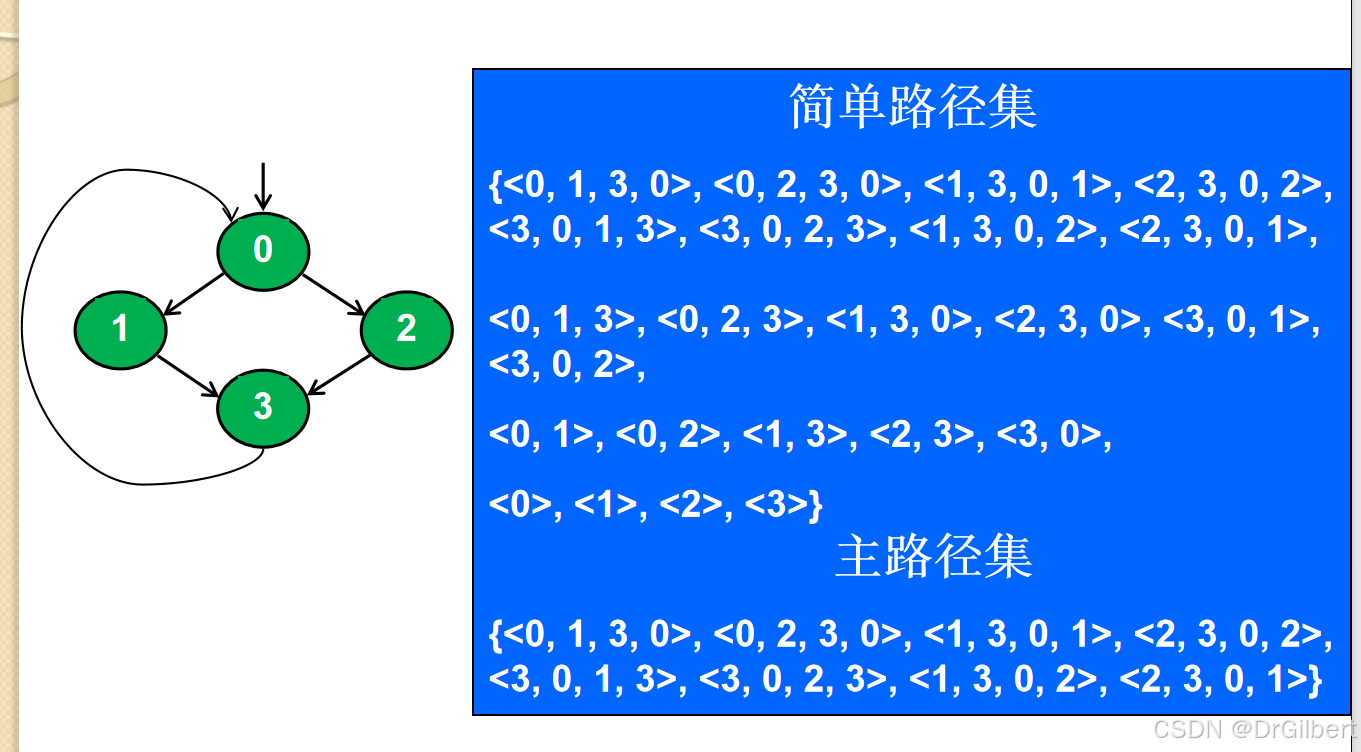
简单路径:无重复节点(除了起点终点),无内部循环。
(一个循环也是简单路径,简单路径的子路径也是简单路径!)
主路径:不是其他简单路径的真子路径。(不是包含关系,但可以是本身)
见之前的笔记软件测试与质量重点
数据流覆盖
定义(变量被赋值):
d
e
f
(
n
)
=
{
x
∣
节点
n
中定义了
x
}
def(n)=\{x|节点n中定义了x\}
def(n)={x∣节点n中定义了x},
d
e
f
(
e
)
=
{
x
∣
边
e
中定义了
x
}
def(e)=\{x|边e中定义了x\}
def(e)={x∣边e中定义了x}
使用(变量被使用):
u
s
e
(
n
)
=
{
x
∣
节点
n
中使用了
x
}
use(n)=\{x|节点n中使用了x\}
use(n)={x∣节点n中使用了x},
u
s
e
(
e
)
=
{
x
∣
边
e
中使用了
x
}
use(e)=\{x|边e中使用了x\}
use(e)={x∣边e中使用了x}
位置对:对于
(
l
i
,
l
j
)
(l_i,l_j)
(li,lj),一个变量
l
i
l_i
li被定义,在
l
j
l_j
lj被使用。
def-use-对:
l
i
=
l
j
l_i=l_j
li=lj的位置对(即处于循环之中)
def-use-路径:从变量被定义,到它被使用期间的路径。(期间没有对该变量重新定义)
def-use
(
n
i
,
n
j
,
v
)
(n_i,n_j,v)
(ni,nj,v):从
n
i
n_i
ni到
n
j
n_j
nj的变量
v
v
v的def-use路径集合。
def-use
(
n
i
)
,
v
(n_i),v
(ni),v:从
n
i
n_i
ni开始的变量
v
v
v的def-use路径集合。(
d
u
(
n
i
,
v
)
=
∪
n
j
d
u
(
n
i
,
n
j
,
v
)
du(n_i,v)=\cup_{n_j}du(n_i,n_j,v)
du(ni,v)=∪njdu(ni,nj,v))
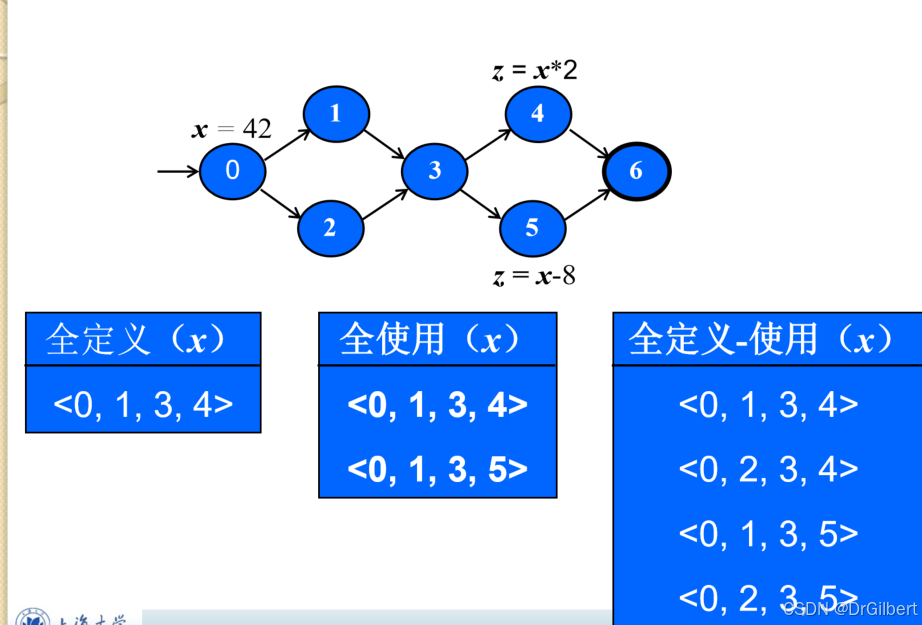
全定义覆盖(all-def):对于每个
d
u
du
du路径集合
S
=
d
u
(
n
,
v
)
S=du(n,v)
S=du(n,v),至少测试
S
S
S中的一条路径。(每个变量,测试至少一条du路径)
全使用覆盖(all-use):对于每个
d
u
du
du路径集合
S
=
d
u
(
n
i
,
n
j
,
v
)
S=du(n_i,n_j,v)
S=du(ni,nj,v),至少测试
S
S
S中的一条路径。(每个du对,测试至少一条du路径)
全du路径覆盖(all-du):测试所有的
S
=
d
u
(
n
i
,
n
j
,
v
)
S=du(n_i,n_j,v)
S=du(ni,nj,v)中的所有路径。(测试所有du路径)
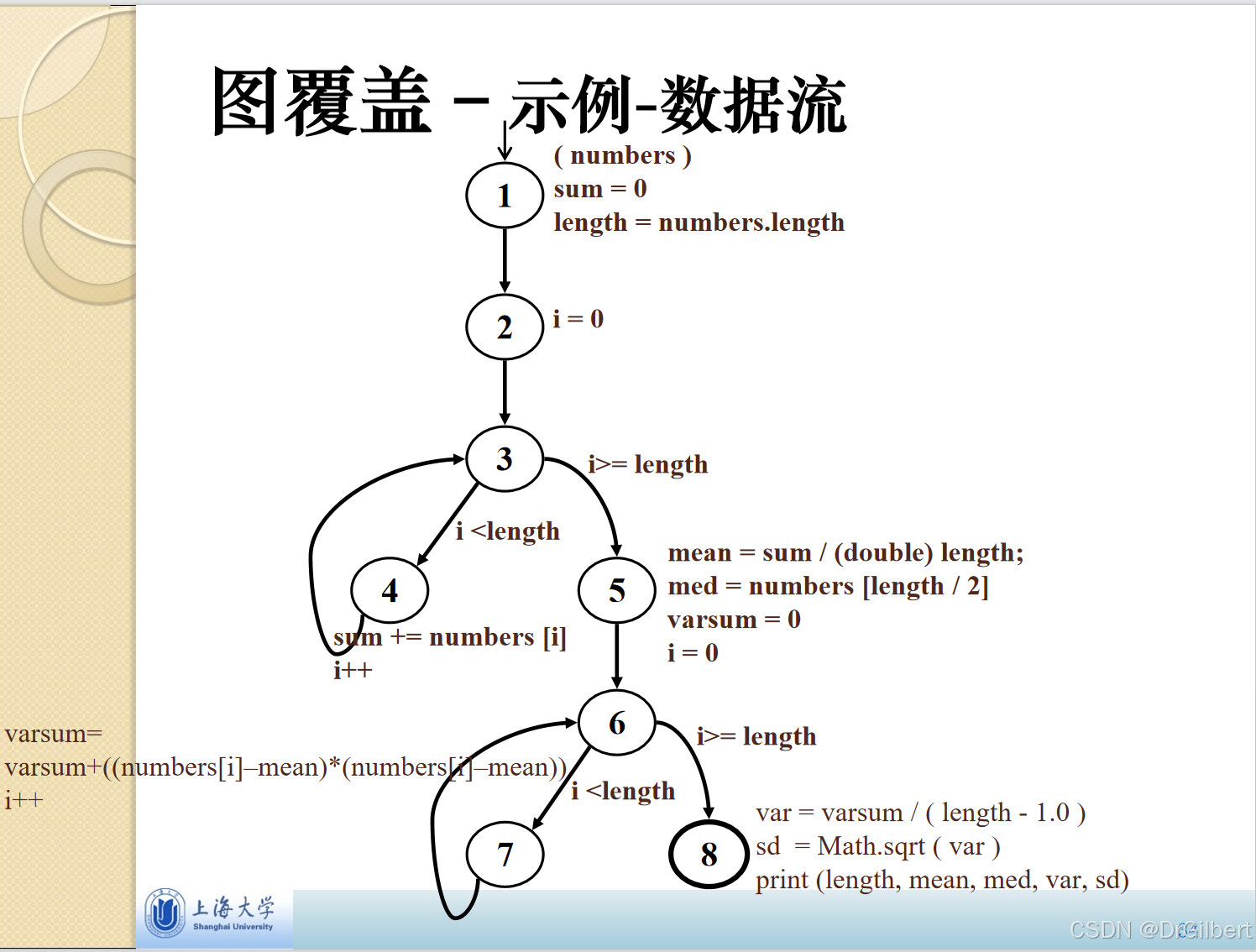
以下流程图为例,先得到每个节点的def与use
由上图可得出:
节点:
d
e
f
(
1
)
=
{
n
u
m
b
e
r
s
,
s
u
m
,
l
e
n
g
t
h
}
def(1)=\{numbers,sum,length\}
def(1)={numbers,sum,length}
d
e
f
(
2
)
=
{
i
}
def(2)=\{i\}
def(2)={i}
d
e
f
(
4
)
=
{
s
u
m
,
i
}
def(4)=\{sum,i\}
def(4)={sum,i}
u
s
e
(
4
)
=
{
s
u
m
,
i
,
n
u
m
b
e
r
s
}
use(4)=\{sum,i,numbers\}
use(4)={sum,i,numbers}
d
e
f
(
5
)
=
{
m
e
a
n
,
m
e
d
,
v
a
r
s
u
m
,
i
}
def(5)=\{mean,med,varsum,i\}
def(5)={mean,med,varsum,i}
u
s
e
(
5
)
=
{
s
u
m
,
l
e
n
g
t
h
,
n
u
m
b
e
r
s
}
use(5)=\{sum,length,numbers\}
use(5)={sum,length,numbers}
d
e
f
(
7
)
=
{
v
a
r
s
u
m
,
i
}
def(7)=\{varsum,i\}
def(7)={varsum,i}
u
s
e
(
7
)
=
{
v
a
r
s
u
m
,
n
u
m
b
e
r
s
,
m
e
a
n
,
i
}
use(7)=\{varsum,numbers,mean,i\}
use(7)={varsum,numbers,mean,i}
d
e
f
(
8
)
=
{
v
a
r
,
s
d
}
def(8)=\{var,sd\}
def(8)={var,sd}
u
s
e
(
8
)
=
{
v
a
r
s
u
m
,
l
e
n
g
t
h
,
v
a
r
,
m
e
a
n
,
m
e
d
,
s
d
}
use(8)=\{varsum,length,var,mean,med,sd\}
use(8)={varsum,length,var,mean,med,sd}
边:
u
s
e
(
3
,
4
)
=
{
i
,
l
e
n
g
t
h
}
use(3,4)=\{i,length\}
use(3,4)={i,length}
u
s
e
(
3
,
5
)
=
{
i
,
l
e
n
g
t
h
}
use(3,5)=\{i,length\}
use(3,5)={i,length}
u
s
e
(
6
,
7
)
=
{
i
,
l
e
n
g
t
h
}
use(6,7)=\{i,length\}
use(6,7)={i,length}
u
s
e
(
6
,
8
)
=
{
i
,
l
e
n
g
t
h
}
use(6,8)=\{i,length\}
use(6,8)={i,length}
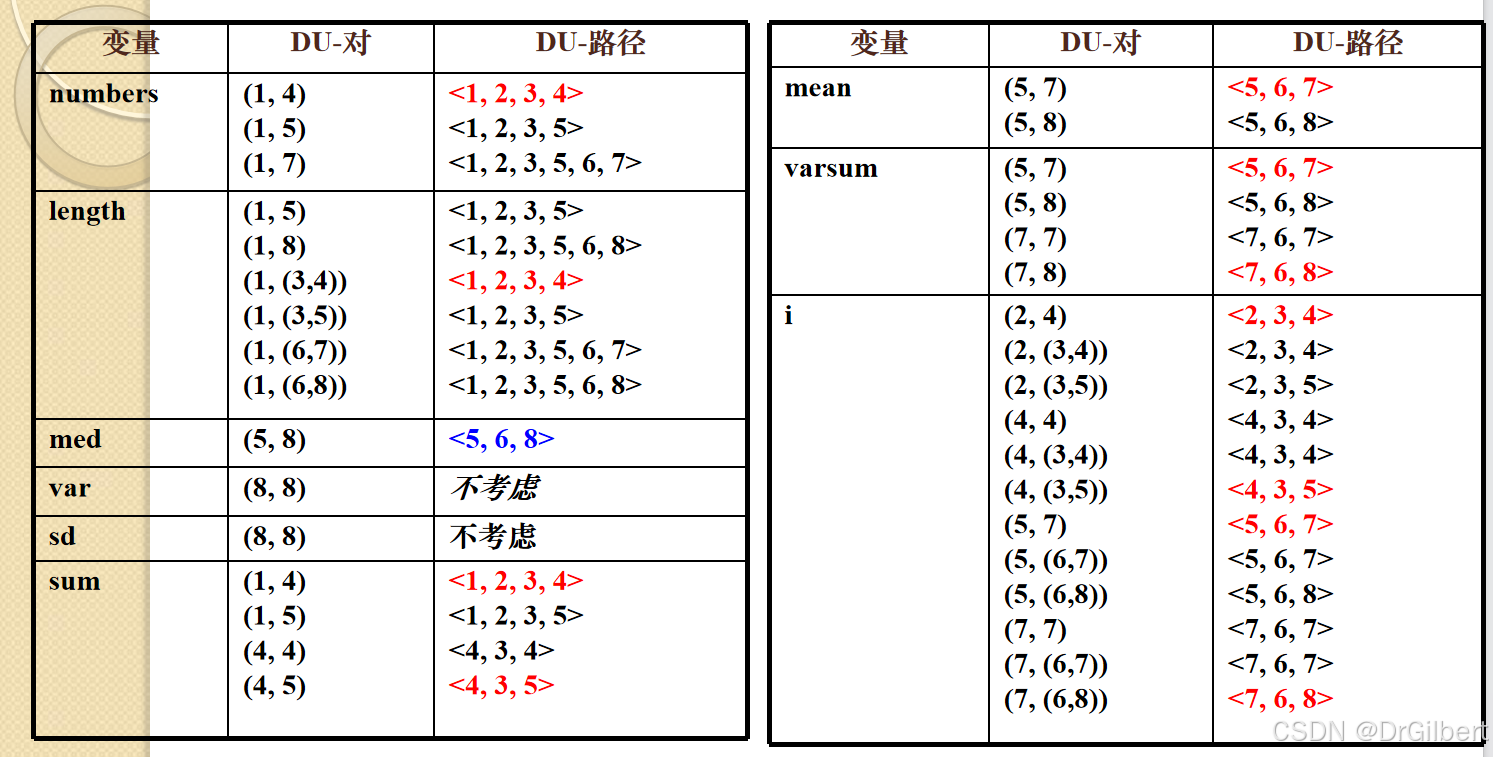
因此可以得到变量的du对:
n
u
m
b
e
r
s
:
(
1
,
4
)
,
(
1
,
5
)
,
(
1
,
7
)
numbers:(1,4),(1,5),(1,7)
numbers:(1,4),(1,5),(1,7)
l
e
n
g
t
h
:
(
1
,
5
)
,
(
1
,
8
)
,
(
1
,
(
3
,
4
)
)
,
(
1
,
(
3
,
5
)
)
,
(
1
,
(
6
,
7
)
)
,
(
1
,
(
6
,
8
)
)
length:(1,5),(1,8),(1,(3,4)),(1,(3,5)),(1,(6,7)),(1,(6,8))
length:(1,5),(1,8),(1,(3,4)),(1,(3,5)),(1,(6,7)),(1,(6,8))
m
e
d
:
(
5
,
8
)
med:(5,8)
med:(5,8)
v
a
r
:
(
8
,
8
)
var:(8,8)
var:(8,8)
s
d
:
(
8
,
8
)
sd:(8,8)
sd:(8,8)
m
e
a
n
:
(
5
,
7
)
,
(
5
,
8
)
mean:(5,7),(5,8)
mean:(5,7),(5,8)
s
u
m
:
(
1
,
4
)
,
(
1
,
5
)
,
(
4
,
4
)
,
(
4
,
5
)
sum:(1,4),(1,5),(4,4),(4,5)
sum:(1,4),(1,5),(4,4),(4,5)
v
a
r
s
u
m
:
(
5
,
7
)
,
(
5
,
8
)
,
(
7
,
7
)
,
(
7
,
8
)
varsum:(5,7),(5,8),(7,7),(7,8)
varsum:(5,7),(5,8),(7,7),(7,8)
i
:
(
2
,
4
)
,
(
2
,
(
3
,
4
)
)
,
(
2
,
(
3
,
5
)
)
,
(
2
,
7
)
,
(
2
,
(
6
,
7
)
)
,
(
2
,
(
6
,
8
)
)
,
i:(2,4),(2,(3,4)),(2,(3,5)),(2,7),(2,(6,7)),(2,(6,8)),
i:(2,4),(2,(3,4)),(2,(3,5)),(2,7),(2,(6,7)),(2,(6,8)),
(
4
,
4
)
,
(
4
,
(
3
,
4
)
)
,
(
4
,
(
3
,
5
)
)
,
(
4
,
7
)
,
(
4
,
(
6
,
7
)
)
,
(
4
,
(
6
,
8
)
)
,
(4,4),(4,(3,4)),(4,(3,5)),(4,7),(4,(6,7)),(4,(6,8)),
(4,4),(4,(3,4)),(4,(3,5)),(4,7),(4,(6,7)),(4,(6,8)),
(
5
,
7
)
,
(
5
,
(
6
,
7
)
)
,
(
5
,
(
6
,
8
)
)
,
(5,7),(5,(6,7)),(5,(6,8)),
(5,7),(5,(6,7)),(5,(6,8)),
(
7
,
7
)
,
(
7
,
(
6
,
7
)
)
,
(
7
,
(
6
,
8
)
)
(7,7),(7,(6,7)),(7,(6,8))
(7,7),(7,(6,7)),(7,(6,8))
于是可以得到所有变量的du路径:
去重后得到du路径:
<
1
,
2
,
3
,
4
>
<1,2,3,4>
<1,2,3,4>
<
1
,
2
,
3
,
5
>
<1,2,3,5>
<1,2,3,5>
<
1
,
2
,
3
,
5
,
6
,
7
>
<1,2,3,5,6,7>
<1,2,3,5,6,7>
<
1
,
2
,
3
,
5
,
6
,
8
>
<1,2,3,5,6,8>
<1,2,3,5,6,8>
<
2
,
3
,
4
>
<2,3,4>
<2,3,4>
<
2
,
3
,
5
>
<2,3,5>
<2,3,5>
<
4
,
3
,
4
>
<4,3,4>
<4,3,4>
<
4
,
3
,
5
>
<4,3,5>
<4,3,5>
<
5
,
6
,
7
>
<5,6,7>
<5,6,7>
<
5
,
6
,
8
>
<5,6,8>
<5,6,8>
<
7
,
6
,
7
>
<7,6,7>
<7,6,7>
<
7
,
6
,
8
>
<7,6,8>
<7,6,8>
因此,
全定义覆盖的测试路径集:
{
1
,
2
,
3
,
4
,
3
,
5
,
6
,
7
,
6
,
8
}
,
{
1
,
2
,
3
,
5
,
6
,
8
}
\{1,2,3,4,3,5,6,7,6,8\},\{1,2,3,5,6,8\}
{1,2,3,4,3,5,6,7,6,8},{1,2,3,5,6,8}
全使用/全du路径覆盖的测试路径集:
{
<
1
,
2
,
3
,
4
,
3
,
5
,
6
,
7
,
6
,
8
>
,
<
1
,
2
,
3
,
4
,
3
,
4
,
3
,
4
,
3
,
5
,
6
,
7
,
6
,
7
,
6
,
7
,
6
,
8
>
,
\{<1,2,3,4,3,5,6,7,6,8>,<1,2,3,4,3,4,3,4,3,5,6,7,6,7,6,7,6,8>,
{<1,2,3,4,3,5,6,7,6,8>,<1,2,3,4,3,4,3,4,3,5,6,7,6,7,6,7,6,8>,
<
1
,
2
,
3
,
5
,
6
,
8
>
,
<
1
,
2
,
3
,
5
,
6
,
7
,
6
,
8
>
}
<1,2,3,5,6,8>,<1,2,3,5,6,7,6,8>\}
<1,2,3,5,6,8>,<1,2,3,5,6,7,6,8>}
三、基于状态的测试
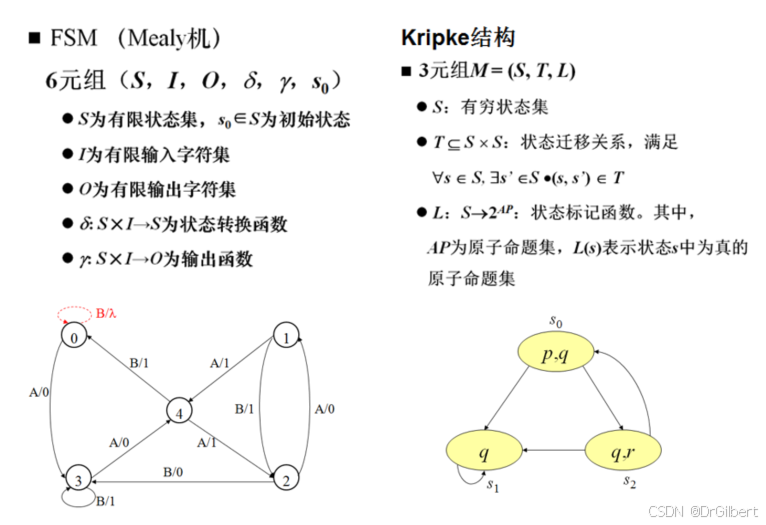
有穷状态机(FSM)
Mealy机/米勒机:
M
=
(
S
,
I
,
O
,
δ
,
γ
,
s
0
)
M=(S,I,O,\delta,\gamma,s_0)
M=(S,I,O,δ,γ,s0)
S
S
S:有限状态集
I
I
I:有限字符输入集
O
O
O:有限字符输出集
δ
\delta
δ:状态转换函数(
S
×
I
→
S
S\times I\rightarrow S
S×I→S)
γ
\gamma
γ:输出函数(
S
×
I
→
O
S\times I\rightarrow O
S×I→O)
s
0
∈
S
s_0\in S
s0∈S:初始状态
Moore机/摩尔机:
M
=
(
S
,
I
,
O
,
δ
,
γ
,
s
0
)
M=(S,I,O,\delta,\gamma,s_0)
M=(S,I,O,δ,γ,s0)
S
S
S:有限状态集
I
I
I:有限字符输入集
O
O
O:有限字符输出集
δ
\delta
δ:状态转换函数(
S
×
I
→
S
S\times I\rightarrow S
S×I→S)
γ
\gamma
γ:输出函数(
S
→
O
S\rightarrow O
S→O,与Mealy机不同之处)
s
0
∈
S
s_0\in S
s0∈S:初始状态
Mealy机与Moore机可以互相转化!
基于有穷状态机的测试(假设FSM是最小的、强联通的、完全的)
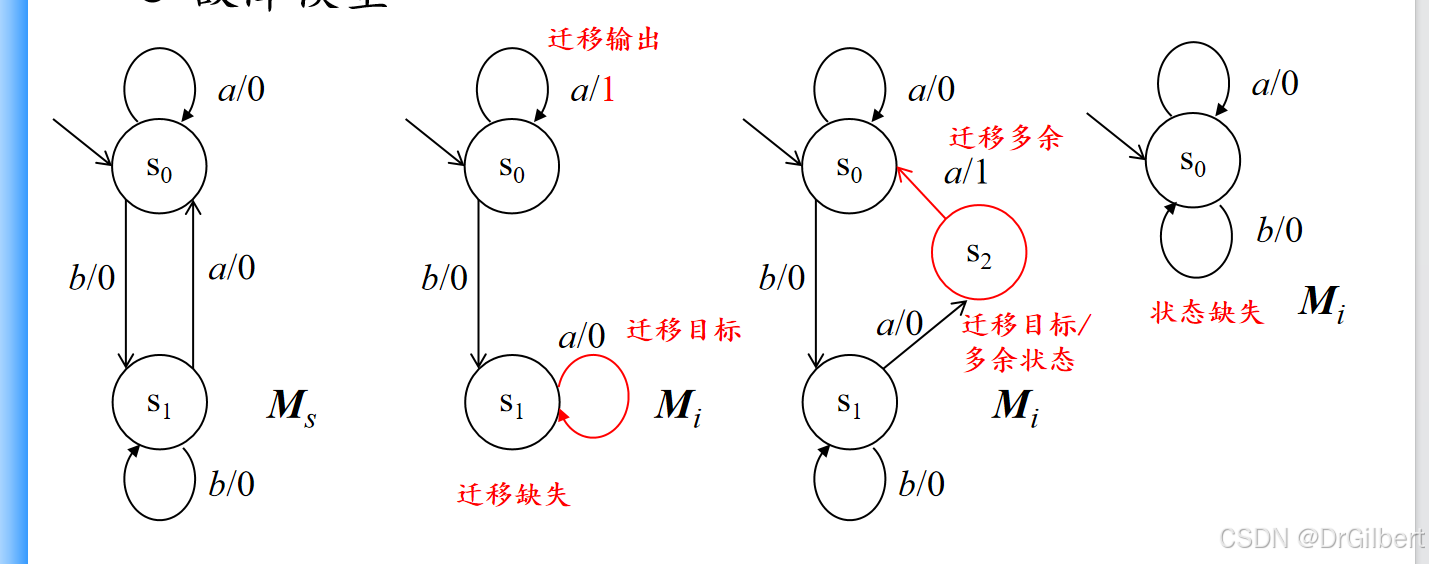
四种错误类型
迁移输出:迁移时输出字符错误
迁移缺失:缺少迁移路径
迁移目标:路径端点错误
迁移多余:多出了额外的迁移状态
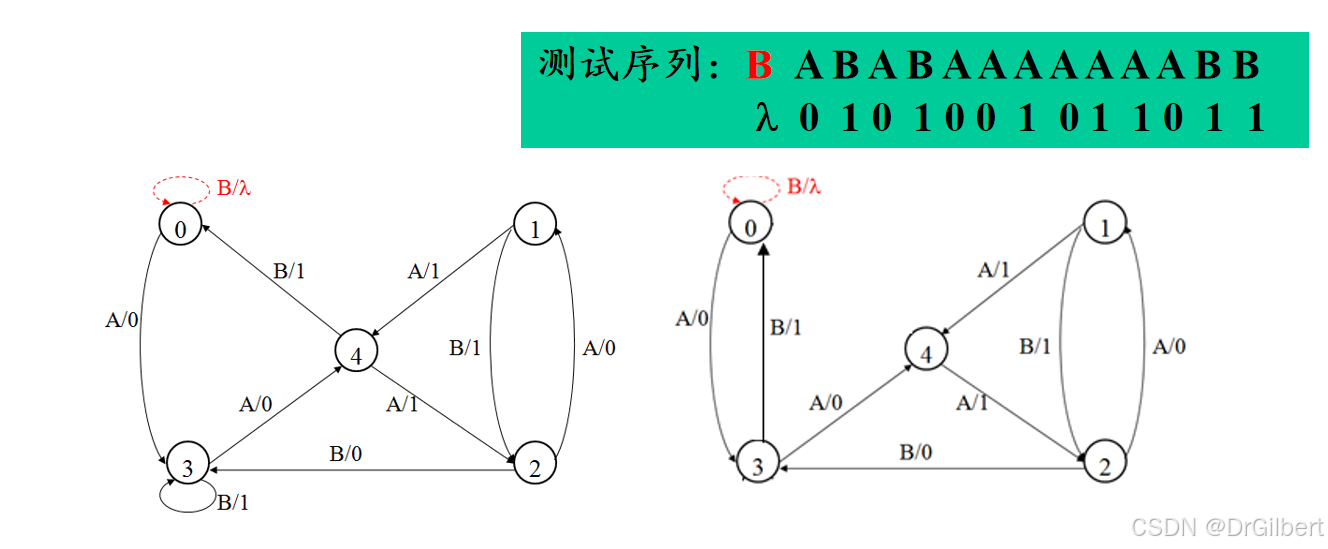
T方法(迁移回路法)
用一条路径覆盖所有边(不一定要最短,检错能力较差,只能检测迁移输出)
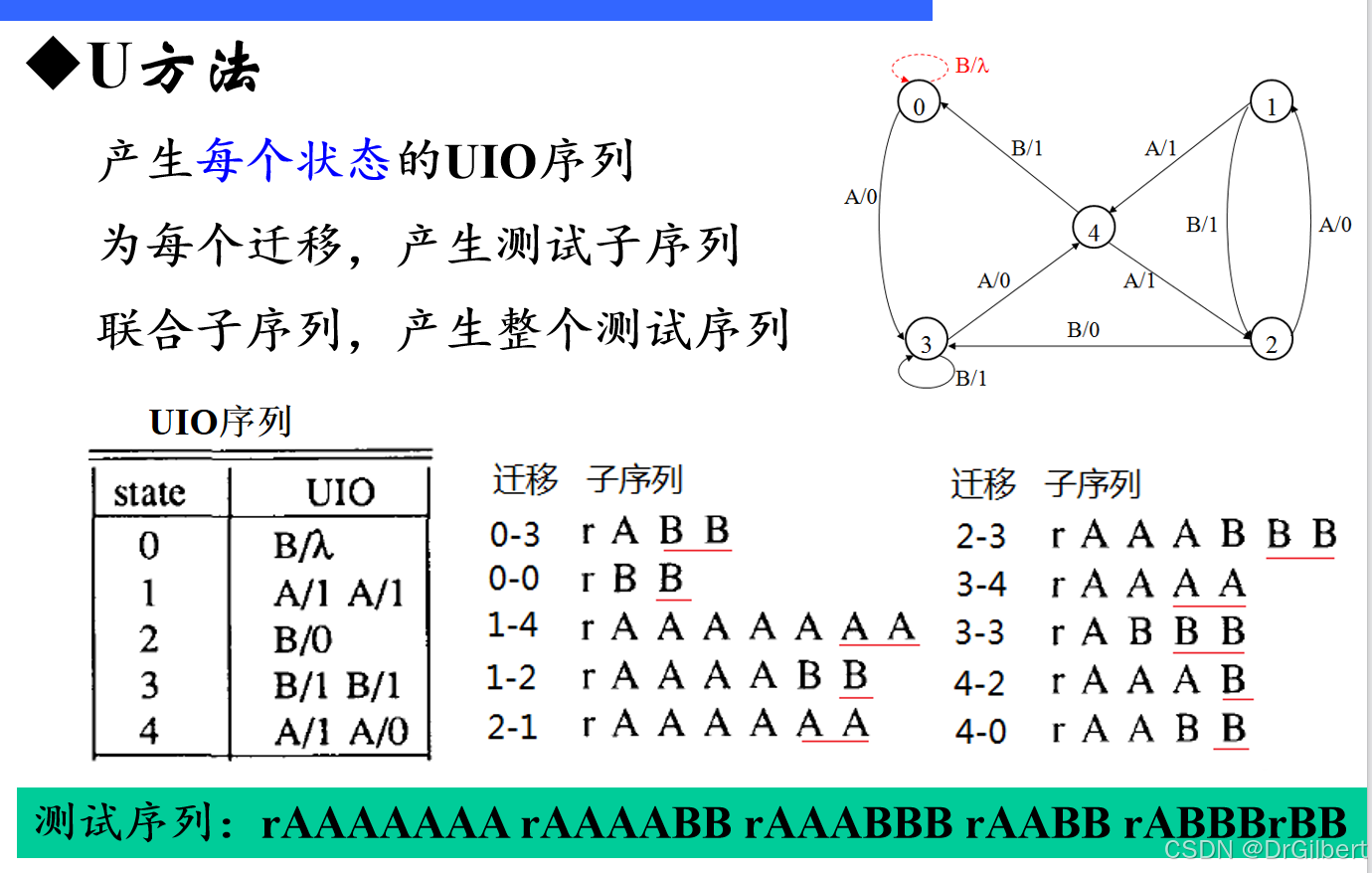
U方法(唯一输入输出/UIO序列检测)
对于每一个状态,从任意一条路径出发,期间不能走到已走过的状态直到不能走为止。(UIO序列可能不唯一!)
UIO序列生成算法:
以上图为例,代入路径DFS求出每一个状态对
(
i
,
j
)
(i,j)
(i,j)的路径向量,表示从状态
i
i
i到状态
j
j
j。
Uv方法:对UIO序列是否唯一进行验证。
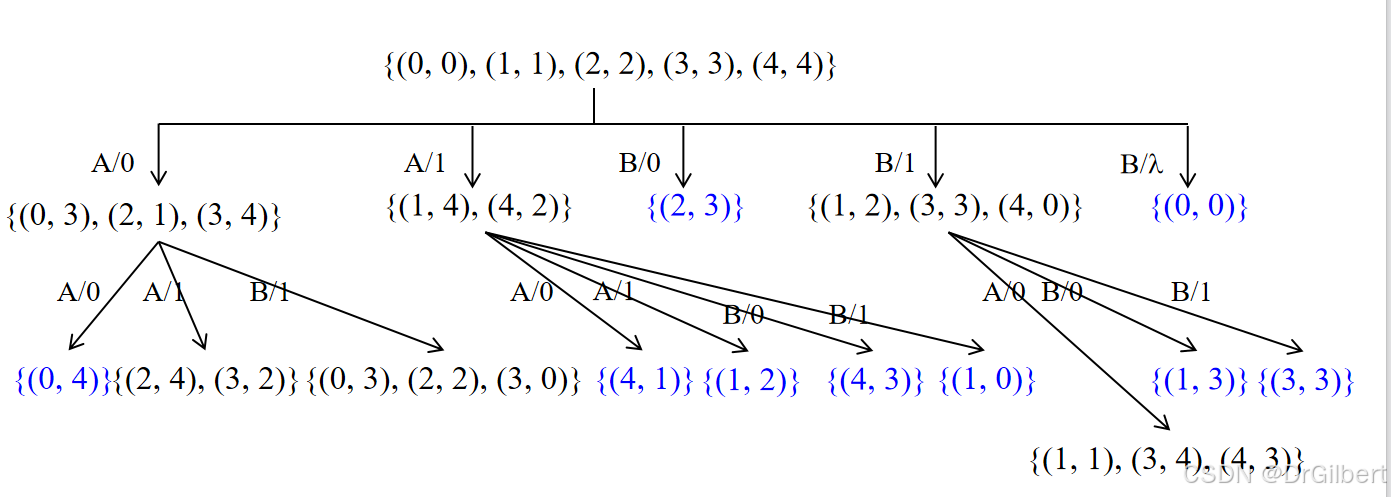
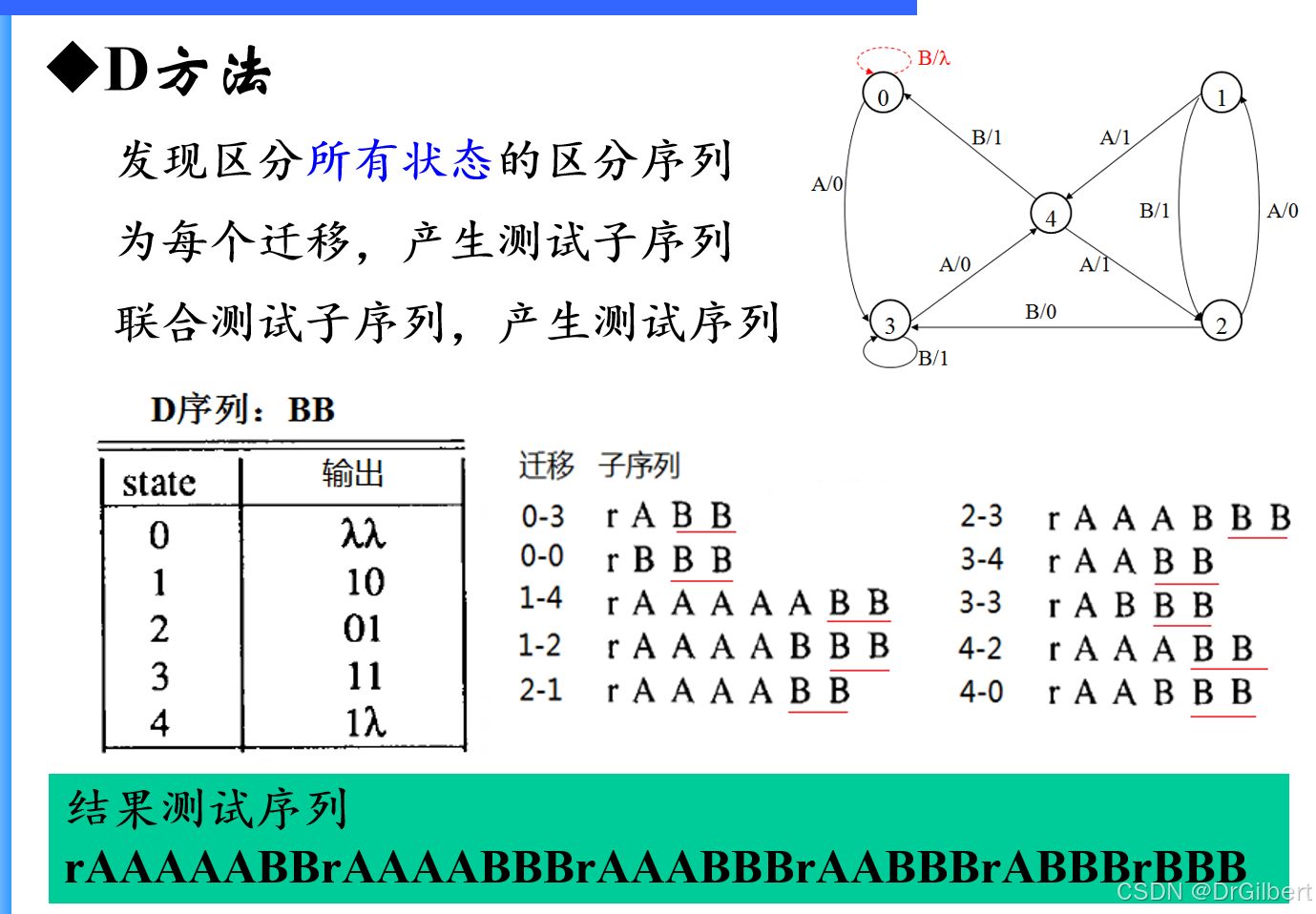
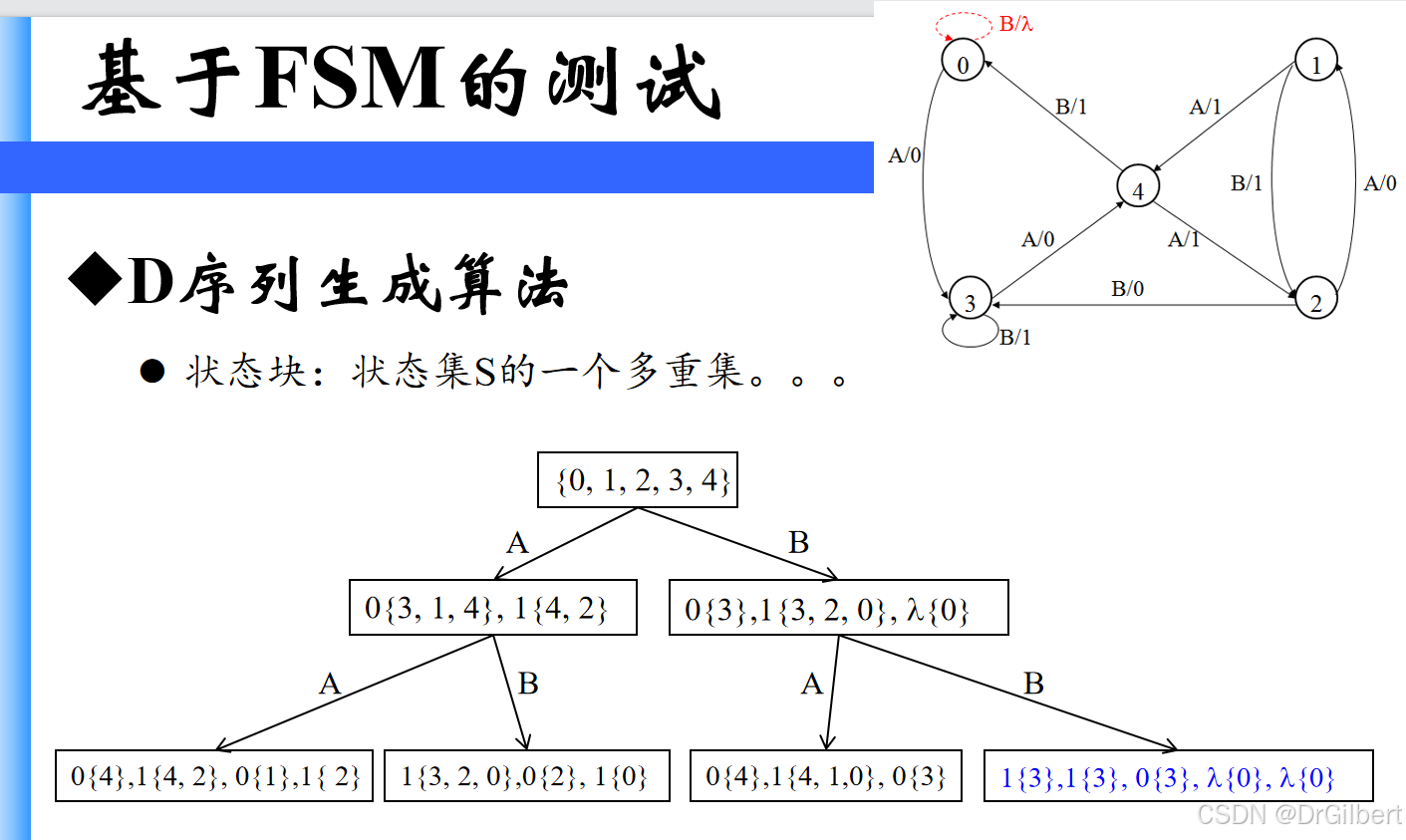
D方法(区分序列)
状态块:
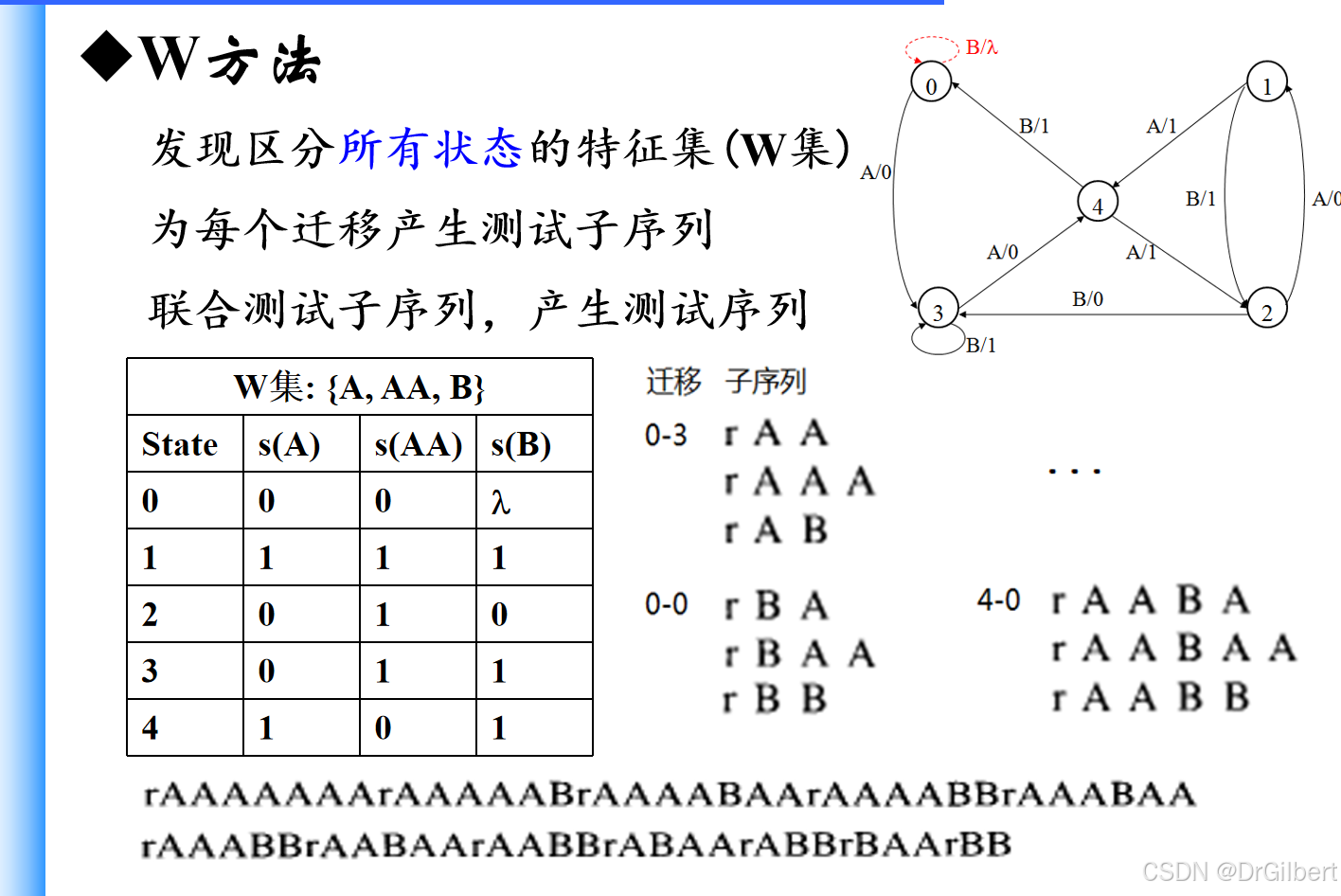
W方法(Characterization set W,特征集)
发现区分所有状态的特征集(W集)
四、输入域测试
见之前笔记软件测试与质量重点
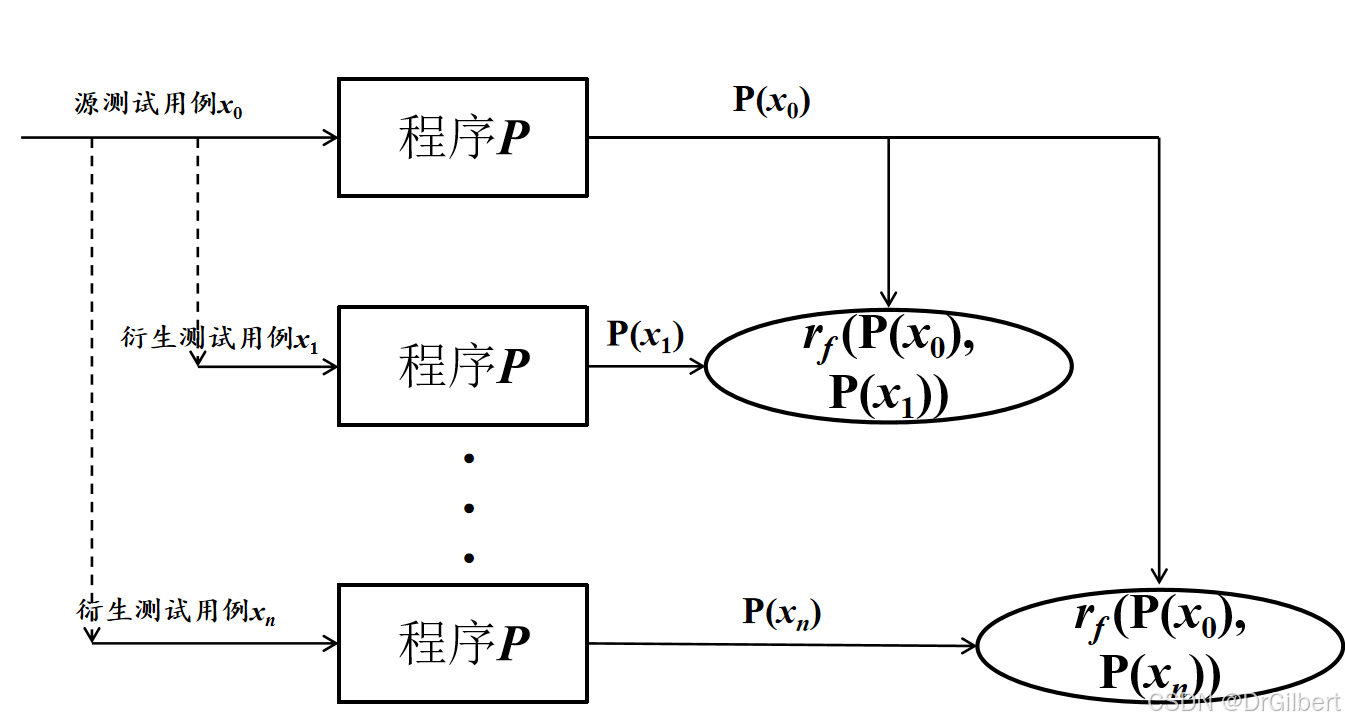
五、蜕变测试
预期输出无法给出的情况下,设计各种输入关系观察输出是否满足预期。
M
R
=
{
(
r
,
r
f
)
}
MR=\{(r,r_f)\}
MR={(r,rf)}
r
r
r:输入数据的关系
r
f
r_f
rf:期望的输出关系
构造数个额外的衍生测试用例
x
i
x_i
xi,并通过
r
f
r_f
rf判断衍生用例测试的结果与源测试用例之间是否符合预期。
但对软件测试人员要求比较高,且设计衍生测试用例不便于自动化。
eg:
P
(
x
)
=
c
o
s
x
P(x)=cosx
P(x)=cosx,
x
0
x_0
x0=38。
构造额外的衍生用例
x
1
=
−
38
,
x
2
=
142
,
x
3
=
218
x_1=-38,x_2=142,x_3=218
x1=−38,x2=142,x3=218
x
1
=
−
x
0
,
r
f
:
c
o
s
(
x
1
)
=
c
o
s
(
x
0
)
x_1=-x_0,r_f:cos(x_1)=cos(x_0)
x1=−x0,rf:cos(x1)=cos(x0)
x
2
=
180
−
x
0
,
r
f
:
c
o
s
(
x
2
)
=
c
o
s
(
x
0
)
x_2=180-x_0,r_f:cos(x_2)=cos(x_0)
x2=180−x0,rf:cos(x2)=cos(x0)
x
3
=
180
+
x
0
,
r
f
:
c
o
s
(
x
3
)
=
−
c
o
s
(
x
0
)
x_3=180+x_0,r_f:cos(x_3)=-cos(x_0)
x3=180+x0,rf:cos(x3)=−cos(x0)
六、基于逻辑表达式的测试
对判定的测试
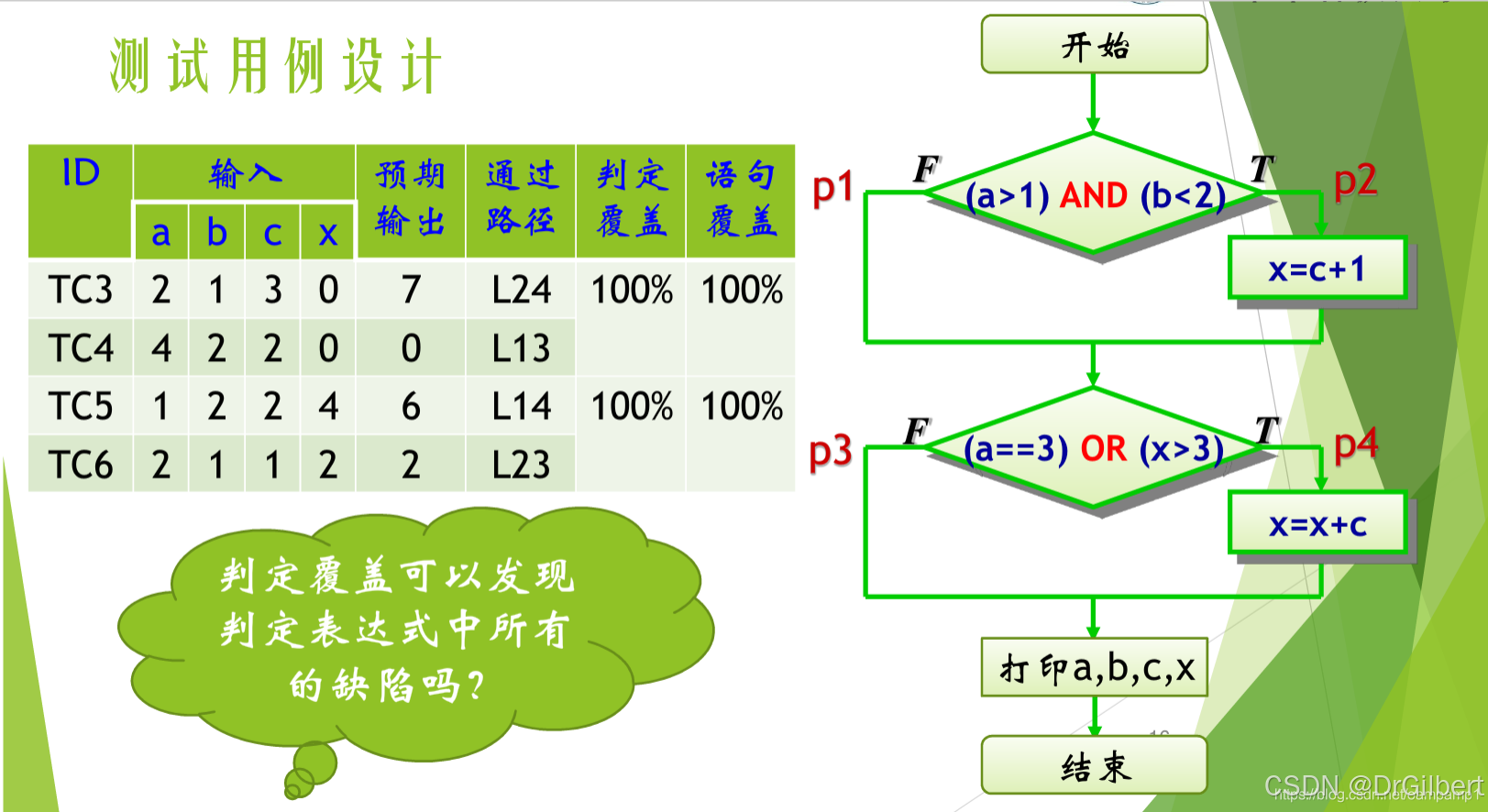
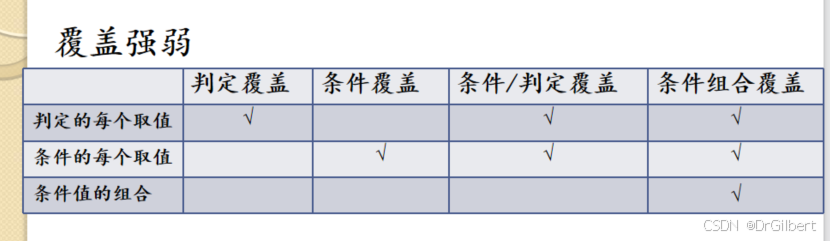
判定覆盖(边覆盖,只关心判定节点整体取值而非子条件)
保证每个判定节点能取到所有可能。
但判定节点为复合判定式子时,判定覆盖只关心其整体取值、因此无法覆盖到每个子条件的取值情况。
如图所示,只需要让两个判定节点两两生成四种结果即可。
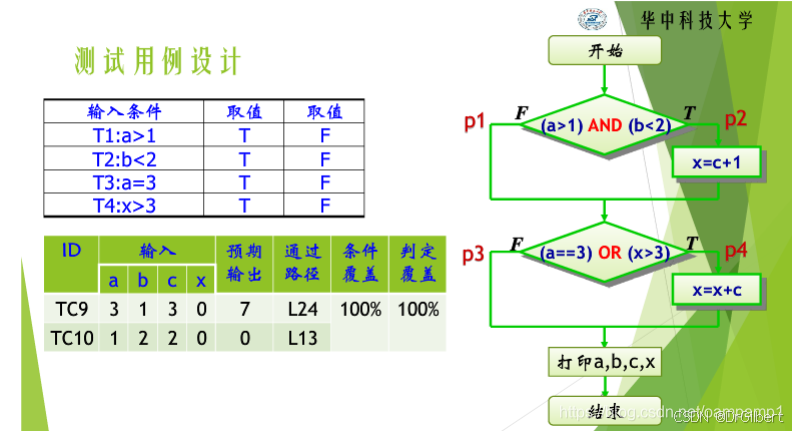
条件覆盖(注重子条件而非整体)
保证程序每个复合判定表达式中,每个 简单判定条件(子条件) 的取真和取假情况至少各执行一次。
条件覆盖不一定满足判定覆盖! 虽然深入检查了判定节点的每一个子条件,但不能保证整体的完全覆盖。
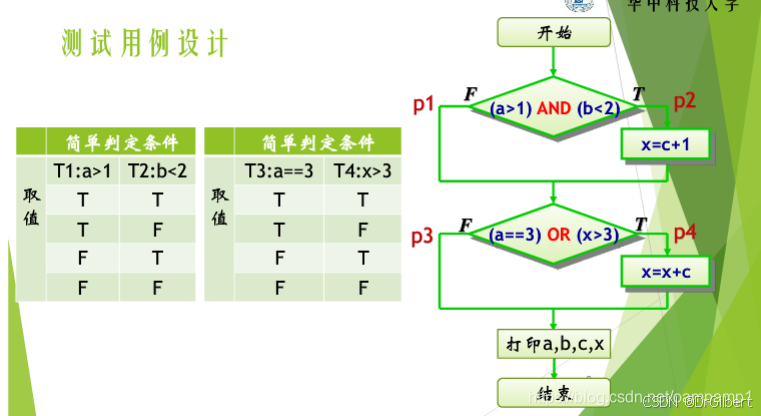
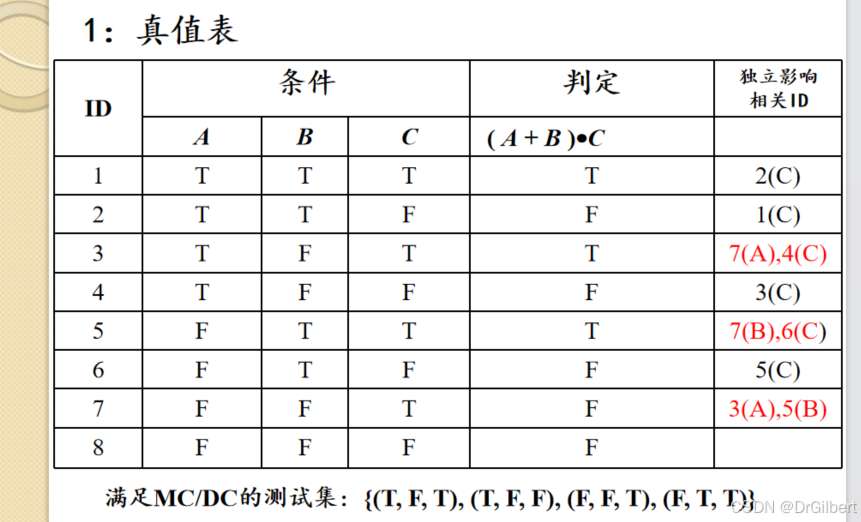
条件组合覆盖/多条件覆盖(真值表)
保证每个判定节点中,所有简单判定条件(子条件)的所有可能取值组合至少执行一次。
方法简单,但测试用例太多,冗余严重(即部分数据的路径相同,且如果子条件前后关联,路径还可能不存在,称为短路)。
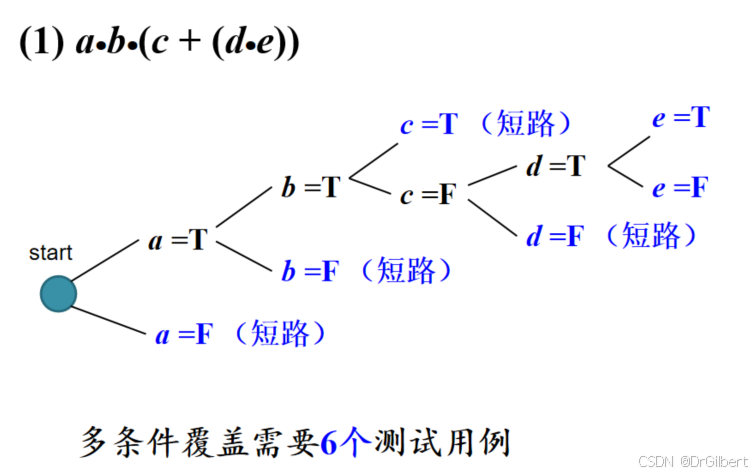
对于一个逻辑表达式,计算其完成条件组合覆盖的最少测试用例数:
MC/DC覆盖(修改条件/判断覆盖)
- 每个判定的每种值至少执行一次
- 每个条件的每种值至少执行一次
- 判定的每个条件都独立影响该判定的结果(即其他不变,单独改变某个条件使得判定值发生变化)
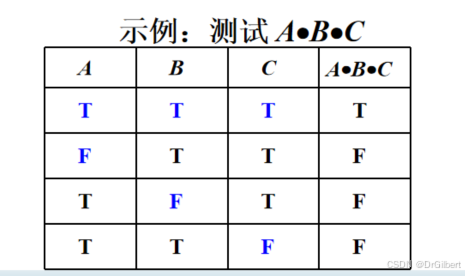
逻辑与(and/ ⋅ \cdot ⋅)的最低测试要求
1.令所有变量为T,使得结果为T。
2.令每个变量单独为F,其他为T,判定为F
(
n
n
n个变量,有
n
+
1
n+1
n+1个测试用例)
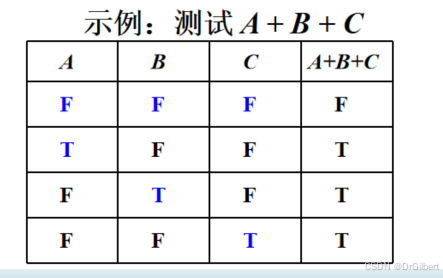
逻辑或(or/+)的最低测试要求
1.令所有变量为T,使得结果为T。
2.令每个变量单独为F,其他为T,判定为T
(
n
n
n个变量,有
n
+
1
n+1
n+1个测试用例)
异或(xor/ ⊕ \oplus ⊕)的最低测试要求
与逻辑或类似,
1.令所有变量为T,使得结果为F。
2.令每个变量单独为T,其他为F,判定为T
(
n
n
n个变量,有
n
+
1
n+1
n+1个测试用例)
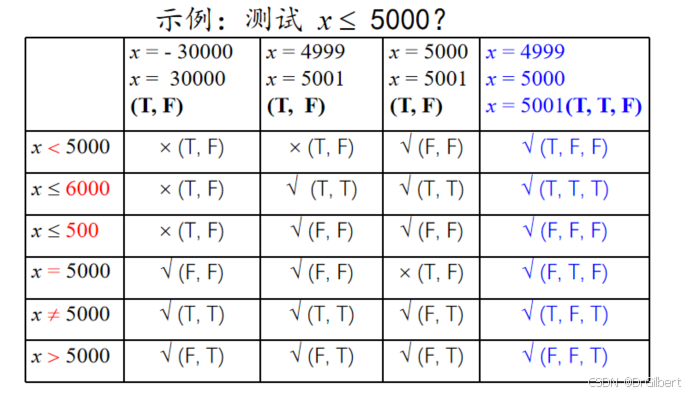
对于关系比较运算( = , ≠ , > , ≥ , < , ≤ =,\neq,>,\geq,<,\leq =,=,>,≥,<,≤)的最低测试要求
选择3类用例:等于、稍大于、稍小于
如何让一个条件独立影响判定
真值表
异或运算
p
c
=
t
r
u
e
p_{c=true}
pc=true:表示
p
p
p中的从句
c
c
c被替换为
t
r
u
e
true
true时的结果
p
c
=
f
a
l
s
e
p_{c=false}
pc=false:表示
p
p
p中的从句
c
c
c被替换为
f
a
l
s
e
false
false时的结果
p
c
=
p
c
=
t
r
u
e
⊕
p
c
=
f
a
l
s
e
p_c=p_{c=true}\oplus p_{c=false}
pc=pc=true⊕pc=false
若该值为
t
r
u
e
true
true则说明
c
c
c独立影响
p
p
p,若为
f
a
l
s
e
false
false则从不影响
p
p
p。
eg1:对于
p
=
a
+
(
b
⋅
c
)
p=a+(b\cdot c)
p=a+(b⋅c),
p
a
=
p
a
=
t
r
u
e
⊕
p
a
=
f
a
l
s
e
p_a=p_{a=true}\oplus p_{a=false}
pa=pa=true⊕pa=false
=
(
t
r
u
e
+
(
b
⋅
c
)
)
⊕
(
f
a
l
s
e
+
(
b
⋅
c
)
)
=(true+(b\cdot c))\oplus (false+(b\cdot c))
=(true+(b⋅c))⊕(false+(b⋅c))
=
t
r
u
e
⊕
(
b
⋅
c
)
=true\oplus (b\cdot c)
=true⊕(b⋅c)(
p
⊕
q
=
(
p
∧
¬
q
)
∨
(
¬
p
∧
q
)
p\oplus q=(p\land \neg q)\lor(\neg p \land q)
p⊕q=(p∧¬q)∨(¬p∧q))
=
¬
(
b
⋅
c
)
=\neg(b\cdot c)
=¬(b⋅c)
=
¬
b
+
¬
c
=\neg b+\neg c
=¬b+¬c
故
a
a
a不独立影响
p
p
p。
eg2:对于
p
=
(
a
⋅
b
)
∨
(
a
⋅
¬
b
)
p=(a\cdot b)\lor(a\cdot \neg b)
p=(a⋅b)∨(a⋅¬b)
p
a
=
p
a
=
t
r
u
e
⊕
p
a
=
f
a
l
s
e
p_a=p_{a=true}\oplus p_{a=false}
pa=pa=true⊕pa=false
=
(
b
∨
¬
b
)
⊕
f
a
l
s
e
=(b\lor\neg b)\oplus false
=(b∨¬b)⊕false
=
t
r
u
e
⊕
f
a
l
s
e
=true\oplus false
=true⊕false
=
t
r
u
e
=true
=true
故
a
a
a独立影响
p
p
p。
p
b
=
p
b
=
t
r
u
e
⊕
p
b
=
f
a
l
s
e
p_b=p_{b=true}\oplus p_{b=false}
pb=pb=true⊕pb=false
=
(
a
)
⊕
(
a
)
=(a)\oplus (a)
=(a)⊕(a)
=
f
a
l
s
e
=false
=false
故
b
b
b不影响
p
p
p。
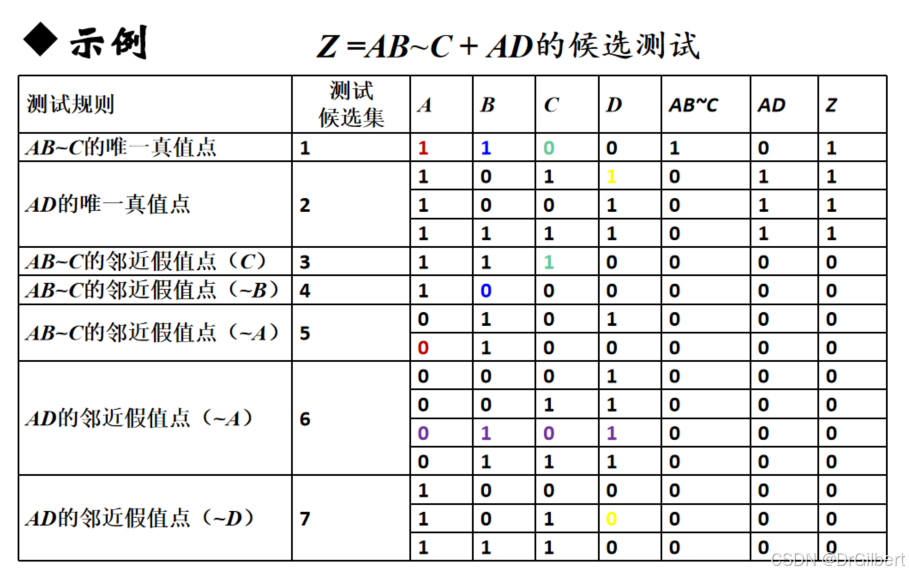
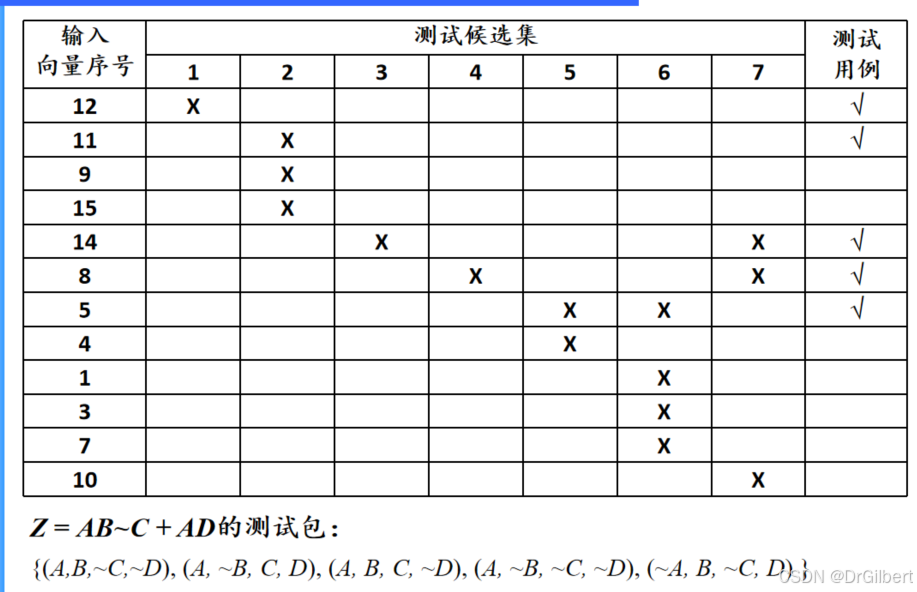
变量否定覆盖
将逻辑表达式转化为析取范式,每个积项/变量独立地影响整个逻辑表达式取值。
唯一真值点:每个积项产生一个变式,使该积项为真而其他为假。
邻近假值点:为每个积项产生一个变式,积项的一个变量为假且其他变量为真时,整个函数值为假。
七、集成测试
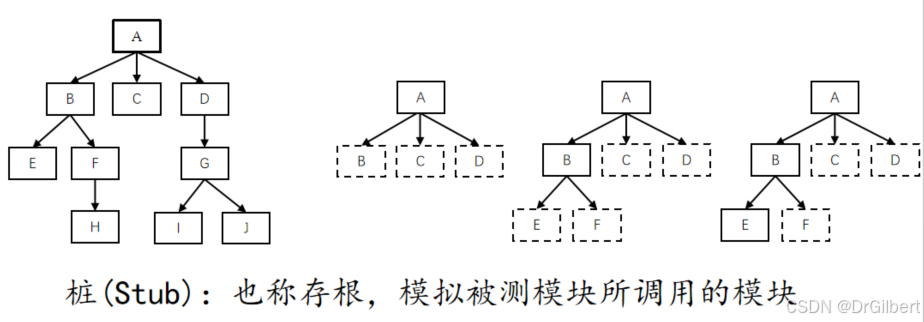
集成策略
自顶向下(类似dfs)
1.集成主控单元,用桩代替隶属于主控单元的所有单元
2.如果单元没有被集成,用实际单元替换桩,实际模块的直接下属单元若存在,也改为桩。
3.对新单元递归到第1步。
自底向上
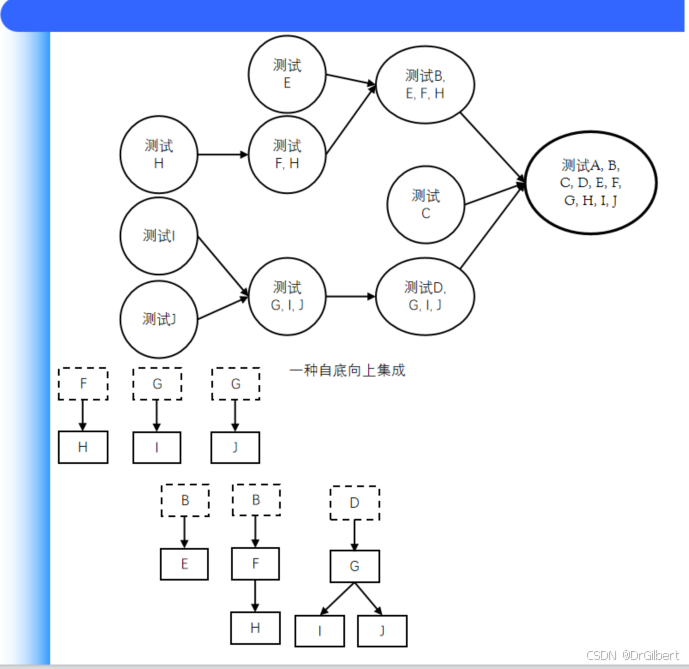
从叶节点模块开始,三层模块作为驱动模块(模拟被测模块的上级模块,接受测试数据并将其传送给被测模块)
三明治集成
将自顶向下&自底向上的组合,桩与驱动的开发量较少。
成对集成
调用图的每条边对应着一次集成,降低了桩/驱动的开发量。
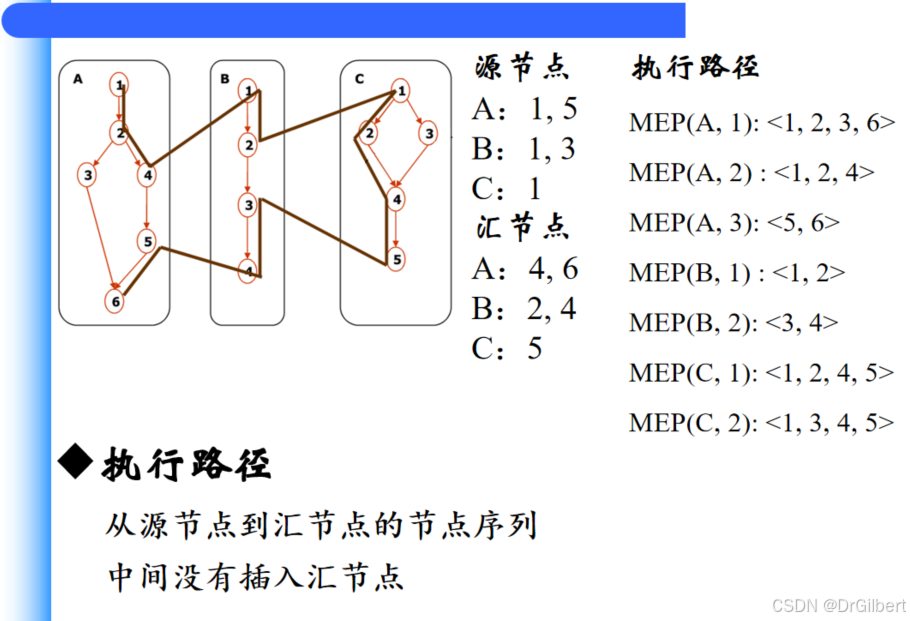
基于路径的集成
源节点:单元起始节点,转移控制到其他单元节点后的紧邻节点
汇节点:单元终止节点,转移控制到其他单元的节点。
一条执行路径从源节点出发汇节点结束,中间没有任何汇节点。
八、系统测试
线索/原子系统功能(ASF)序列:从端口输入事件开始,遍历程序,到端口输出事件结束。
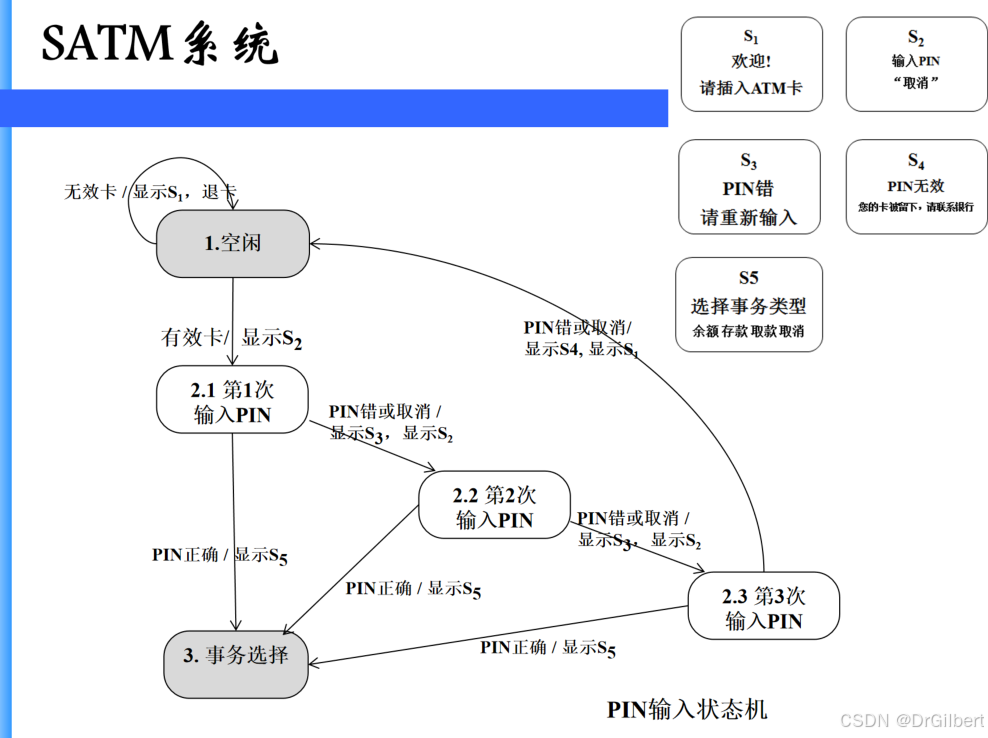
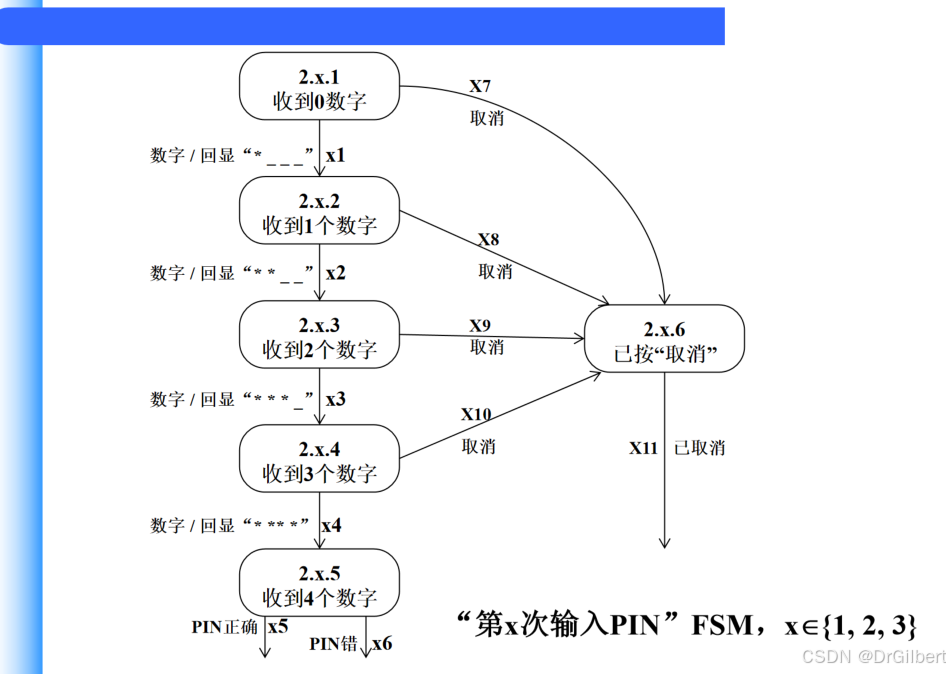
以该SATM系统为例,由该流程图可知线索:
有效卡->显示
S
1
S_1
S1
卡错->显示
S
2
S_2
S2
PIN正确->显示
S
3
S_3
S3
PIN错->显示
S
4
S_4
S4
取消->显示
S
5
S_5
S5
有穷状态机:
测试线索:节点覆盖、边覆盖等…
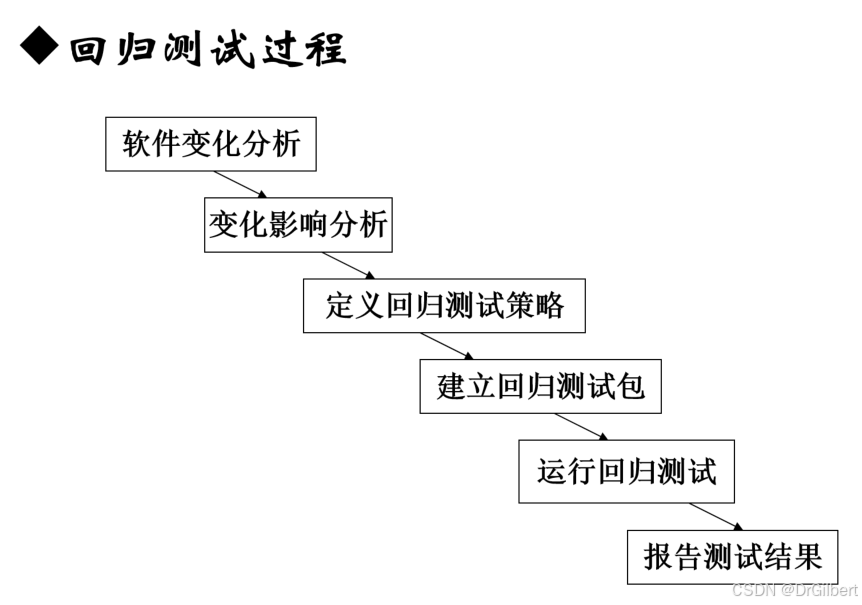
九、回归测试
对已经测试过、修改过的程序重新测试,以发现因为修改可能引起的错误。
测试方法:
(1)全部重新测试(适用于大部分被修改或测试用例不多)
(2)有选择的重新测试(测试用例很多或系统改动很小)
组测试:一个模块单独运行正常,但整体集成时失败。
波漪效应分析:寻找所有受影响部分与潜在的受影响部分,确保修改后仍保持一致性与完整性。(这些部分链在一起形成模块防火墙)
程序切片(往往生成数量很大的切片集):把程序分为若干段语句集,去影响里面的语句变量值。能自动化帮助进行识别潜在波及影响。
十、符号执行
用抽象的符号表示变量的值模拟程序运行,需要维护状态与路径约束。
动态符号执行:Concolic
对于第一行,具体值
x
=
1
,
y
=
1
x=1,y=1
x=1,y=1,符号状态
x
=
x
0
,
y
=
y
0
x=x_0,y=y_0
x=x0,y=y0,路径情况为
T
r
u
e
True
True。
执行z=double(y)时,具体值
x
=
2
,
y
=
1
,
z
=
2
x=2,y=1,z=2
x=2,y=1,z=2,符号状态
x
=
x
0
,
y
=
y
0
,
z
=
2
∗
y
0
x=x_0,y=y_0,z=2*y_0
x=x0,y=y0,z=2∗y0,路径情况为
T
r
u
e
True
True。
执行if(z==x)时,具体值
x
=
2
,
y
=
1
,
z
=
2
x=2,y=1,z=2
x=2,y=1,z=2,符号状态
x
=
x
0
,
y
=
y
0
,
z
=
2
∗
y
0
x=x_0,y=y_0,z=2*y_0
x=x0,y=y0,z=2∗y0,路径情况
2
∗
y
0
=
=
x
0
2*y_0==x_0
2∗y0==x0。
跳转到if(x>y+10)执行时,具体值
x
=
2
,
y
=
1
,
z
=
2
x=2,y=1,z=2
x=2,y=1,z=2,符号状态
x
=
x
0
,
y
=
y
0
,
z
=
2
∗
y
0
x=x_0,y=y_0,z=2*y_0
x=x0,y=y0,z=2∗y0,路径情况
(
2
∗
y
0
=
=
x
0
)
∧
(
x
0
≤
y
0
+
10
)
(2*y_0==x_0) \wedge (x_0 \leq y_0+10)
(2∗y0==x0)∧(x0≤y0+10)。
solve:
(
2
∗
y
0
)
=
=
(
x
0
∧
x
0
>
y
0
+
10
)
(2*y_0)==(x_0 \wedge x_0>y_0+10)
(2∗y0)==(x0∧x0>y0+10)
solution:
x
0
=
30
,
y
0
=
15
x_0=30,y_0=15
x0=30,y0=15。
十一、模型检测(自动的、基于模型的性质验证方法)
Kripke结构:
3元组
M
=
(
S
,
T
,
L
)
M=(S,T,L)
M=(S,T,L)
S
S
S:有穷状态集
T
⊆
S
×
S
T\subseteq S\times S
T⊆S×S:状态迁移关系
L
:
S
→
2
A
P
L:S\rightarrow2^{AP}
L:S→2AP:状态标记函数
路径
π
=
<
s
1
,
s
2
,
s
3
,
.
.
.
>
\pi=<s_1,s_2,s_3,...>
π=<s1,s2,s3,...>,也可以表示为
s
1
→
s
2
→
s
3
→
.
.
.
s_1\rightarrow s_2\rightarrow s_3 \rightarrow ...
s1→s2→s3→...,用
π
3
:
s
3
→
s
4
→
.
.
.
\pi^3:s_3\rightarrow s_4\rightarrow ...
π3:s3→s4→...
时态逻辑
线性时间逻辑(路径集合,LTL)
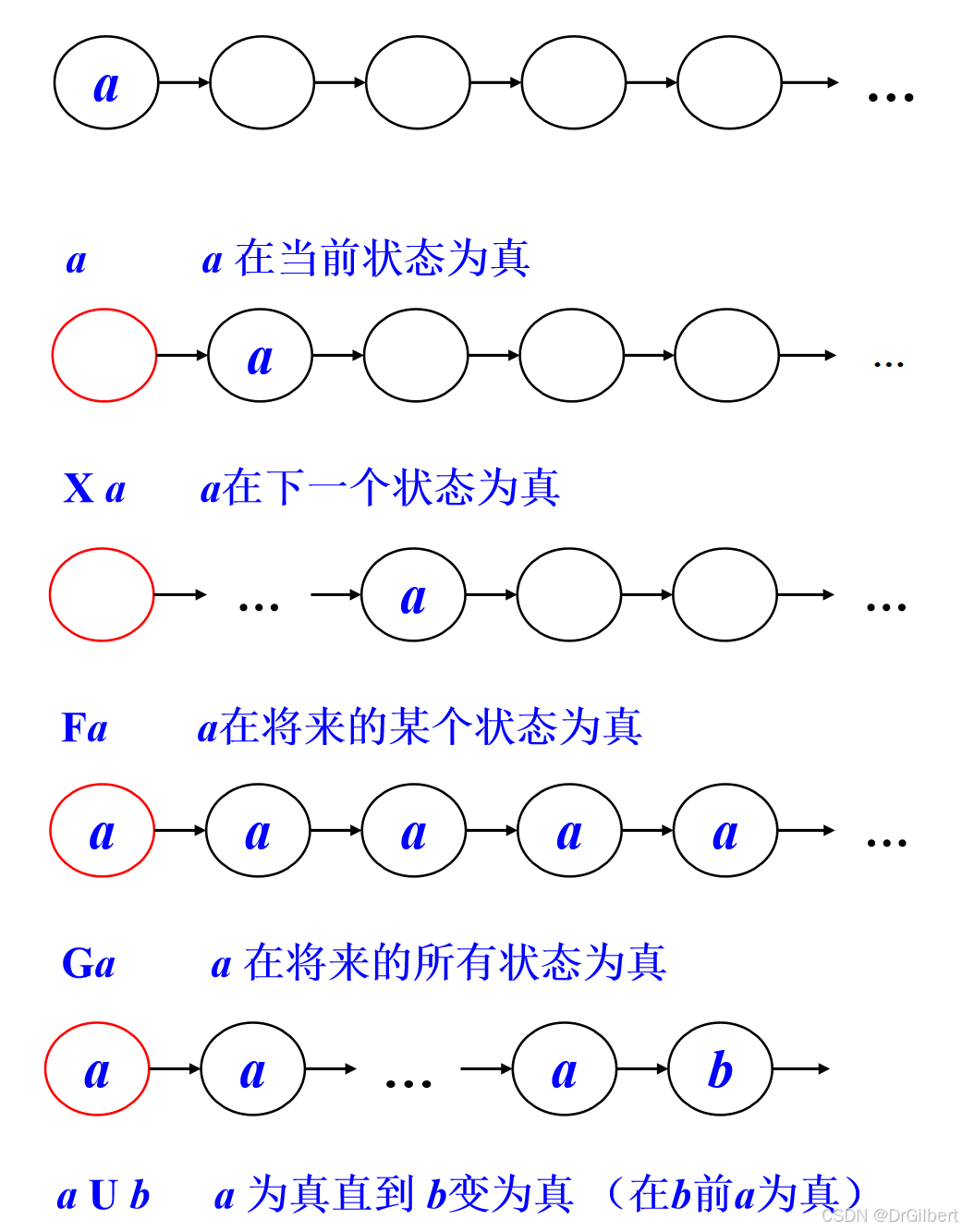
X:下一状态(
X
a
Xa
Xa:
a
a
a在下一个状态为真)
F:将来状态(
F
a
Fa
Fa:
a
a
a在将来的某个状态为真)
G:所有将来状态(
G
a
Ga
Ga:
a
a
a在将来的所有状态为真)
U:直到…(
a
U
b
aUb
aUb:在
b
b
b前
a
a
a为真)
符号优先级:
¬
、
X
、
F
、
G
¬、X、F、G
¬、X、F、G> 二元时序操作
U
U
U>
∧
、
∨
\wedge、\vee
∧、∨>
→
\rightarrow
→
互斥:
安全性:坏事永不发生(任何时候临界区不能存在多于1个进程)
活性:好事总会发生(只要请求进入临界区,会被允许进入)
无阻性:进程总可以请求进入临界区
进程状态:
n
n
n:非临界
t
t
t:试图进入
c
c
c:处于临界
计算树逻辑(树形结构,CTL)
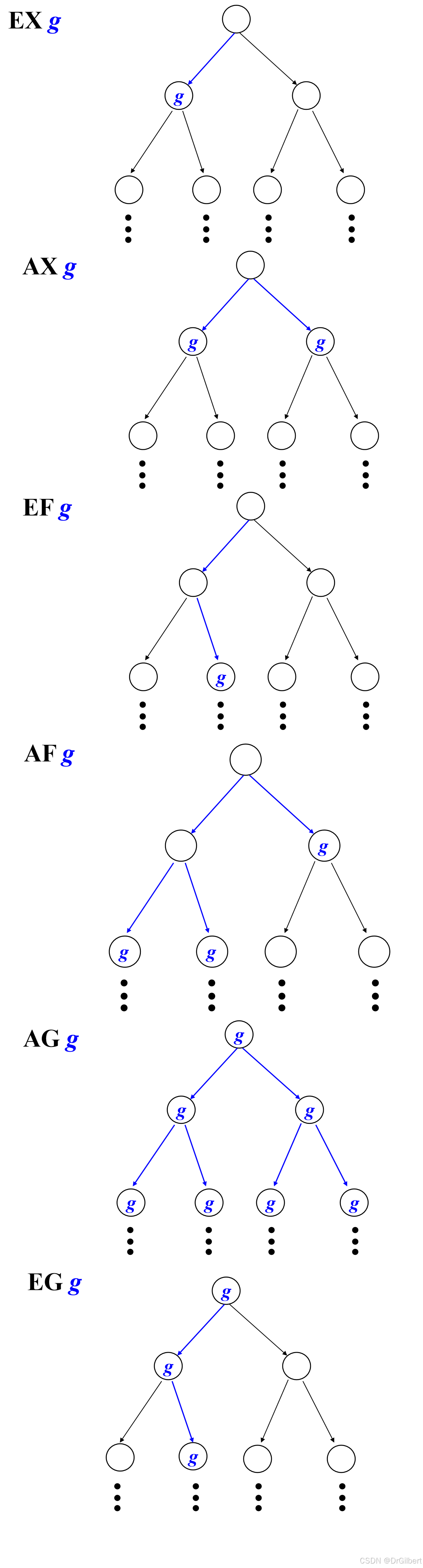
A:所有路径
E:存在路径
X:下一状态
F:将来状态
G:所有将来状态
U:直到…
由上述组合出8个状态
A
X
,
E
X
,
A
G
,
E
G
,
A
U
,
A
F
,
E
F
AX, EX, AG, EG, AU, AF, EF
AX,EX,AG,EG,AU,AF,EF。
优先级:
¬
,
A
G
,
E
G
,
A
F
,
E
F
,
A
X
,
E
X
¬,AG, EG, AF, EF,AX, EX
¬,AG,EG,AF,EF,AX,EX>
∧
、
∨
\wedge、\vee
∧、∨>
→
,
A
U
,
E
U
\rightarrow,AU,EU
→,AU,EU。
CTL与LTL的比较
LTL不能表达:任何状态可以到达 restart 状态,但LTL可以描述在所有路径上选择一个范围
CTL的模型检测算法
对于
M
=
(
S
,
T
,
L
)
,
s
0
∈
S
,
φ
,
\mathcal{M}=(S,T,L),s_0\in S,\varphi,
M=(S,T,L),s0∈S,φ,求
M
,
s
0
∣
=
φ
\mathcal{M},s_0|=\varphi
M,s0∣=φ。
缺点:模型是线性的,规模随变量个数成指数增长
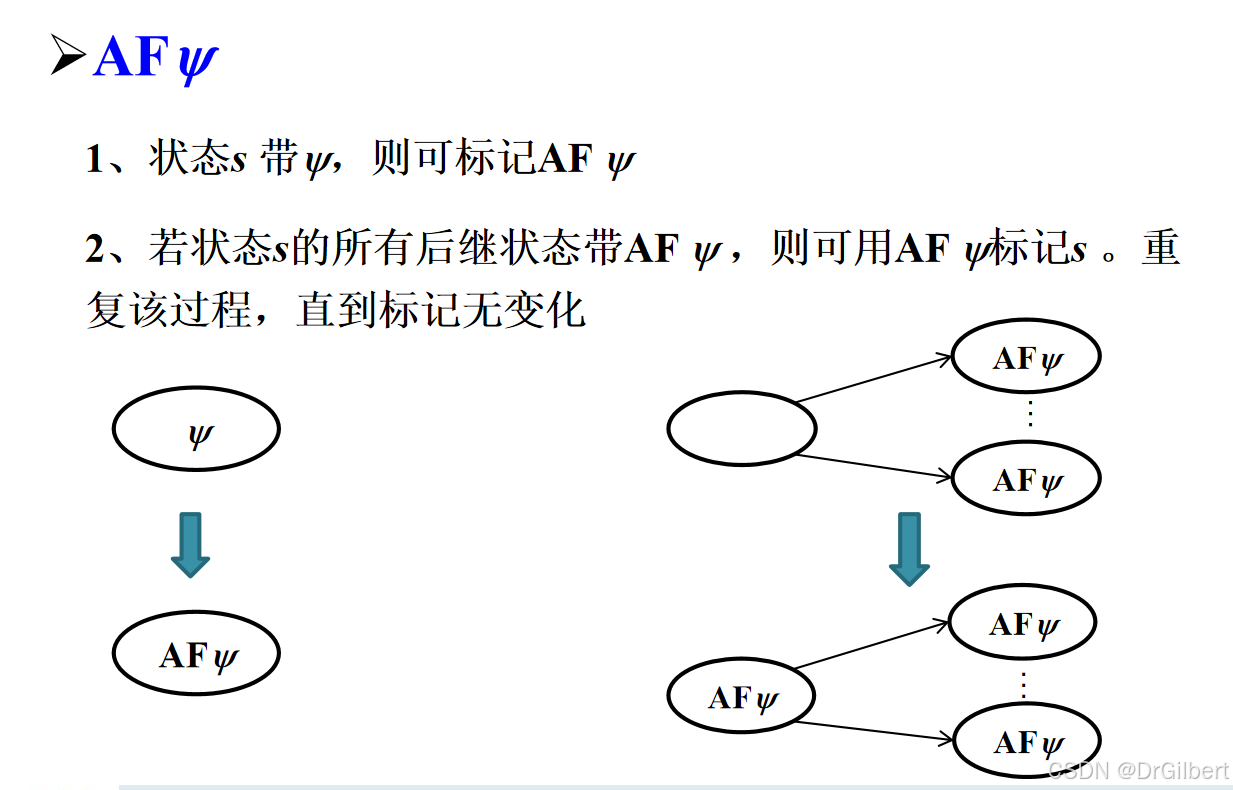
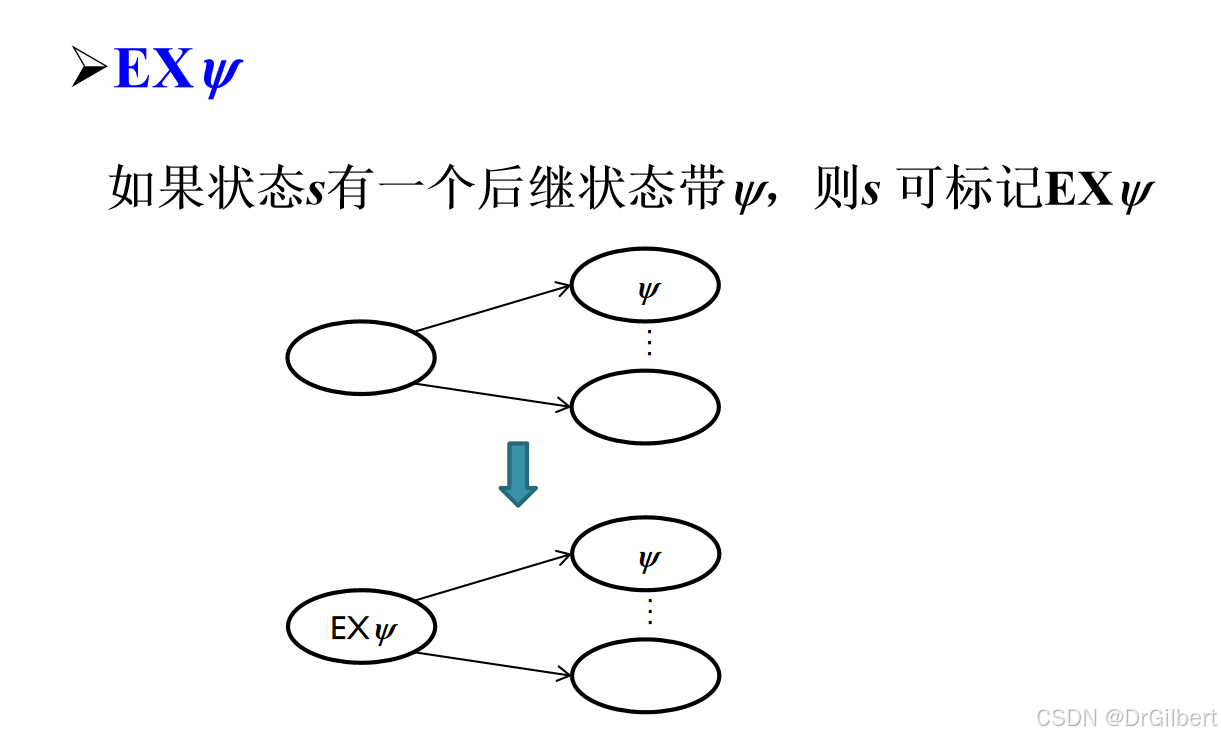
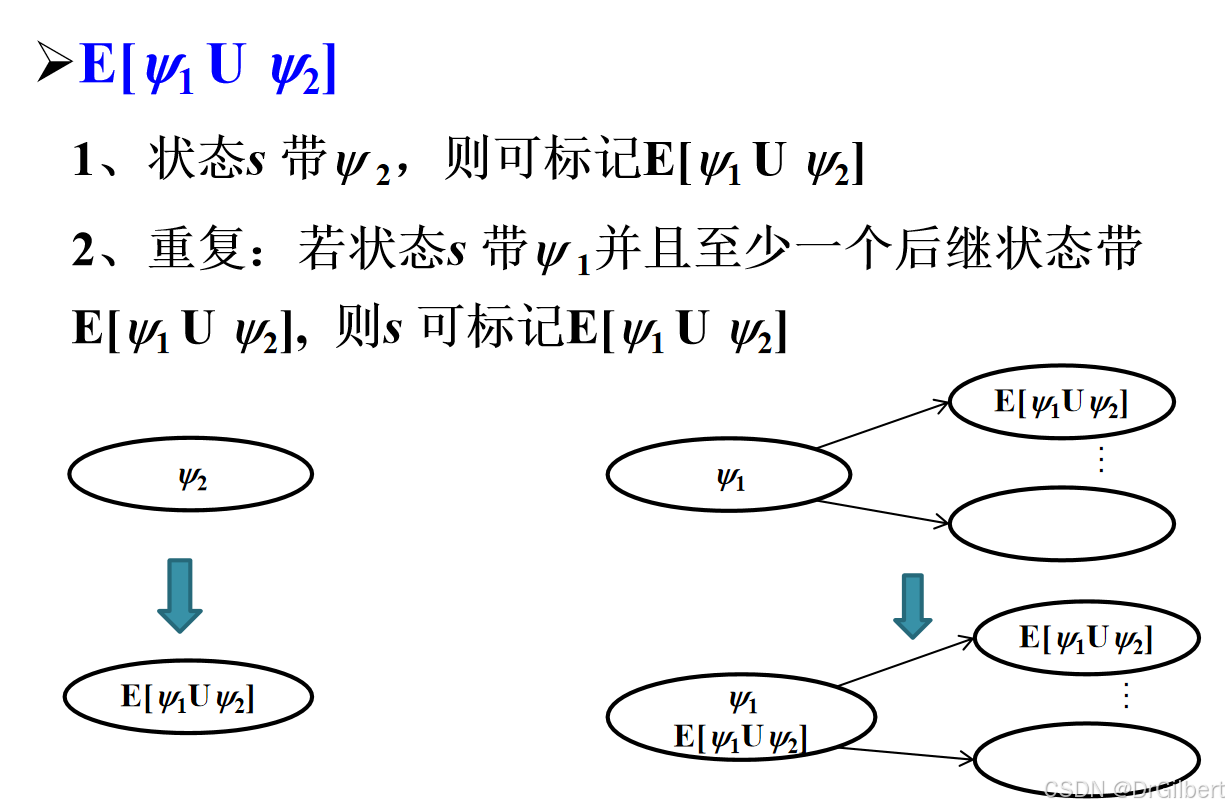
标记算法 S A T ( φ ) SAT(\varphi) SAT(φ)
标记 ψ \psi ψ可以标记的状态:
⊥
\bot
⊥:没有任何状态带标记
⊥
\bot
⊥。
p
p
p:若
p
∈
L
(
s
)
p\in L(s)
p∈L(s),则
s
s
s带标记
p
p
p。
ψ
1
∧
ψ
2
\psi_1\wedge\psi_2
ψ1∧ψ2:若状态
s
s
s同时拥有标记
ψ
1
\psi_1
ψ1与
ψ
2
\psi_2
ψ2,则用
ψ
1
∧
ψ
2
\psi_1\wedge\psi_2
ψ1∧ψ2标记。
¬
ψ
1
¬\psi_1
¬ψ1:状态
s
s
s没有
ψ
1
\psi_1
ψ1。
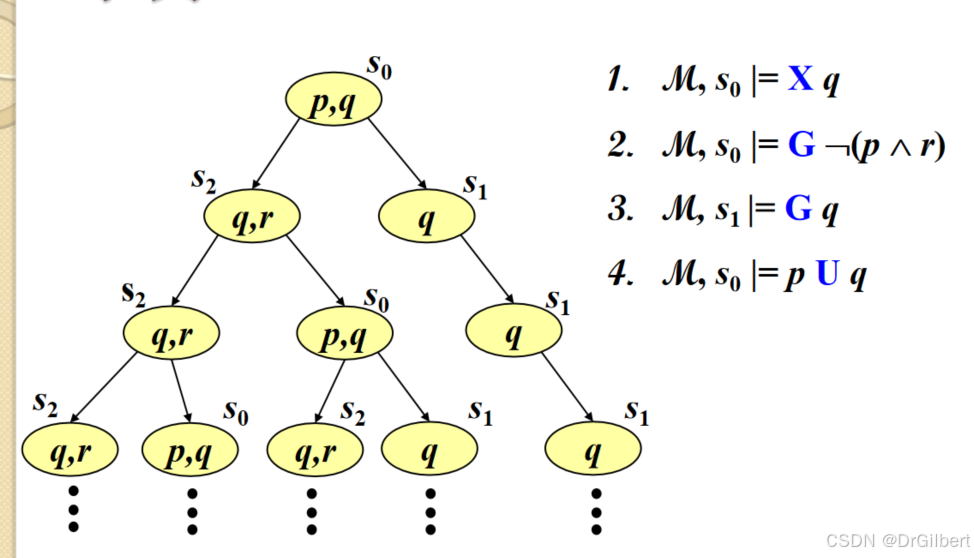
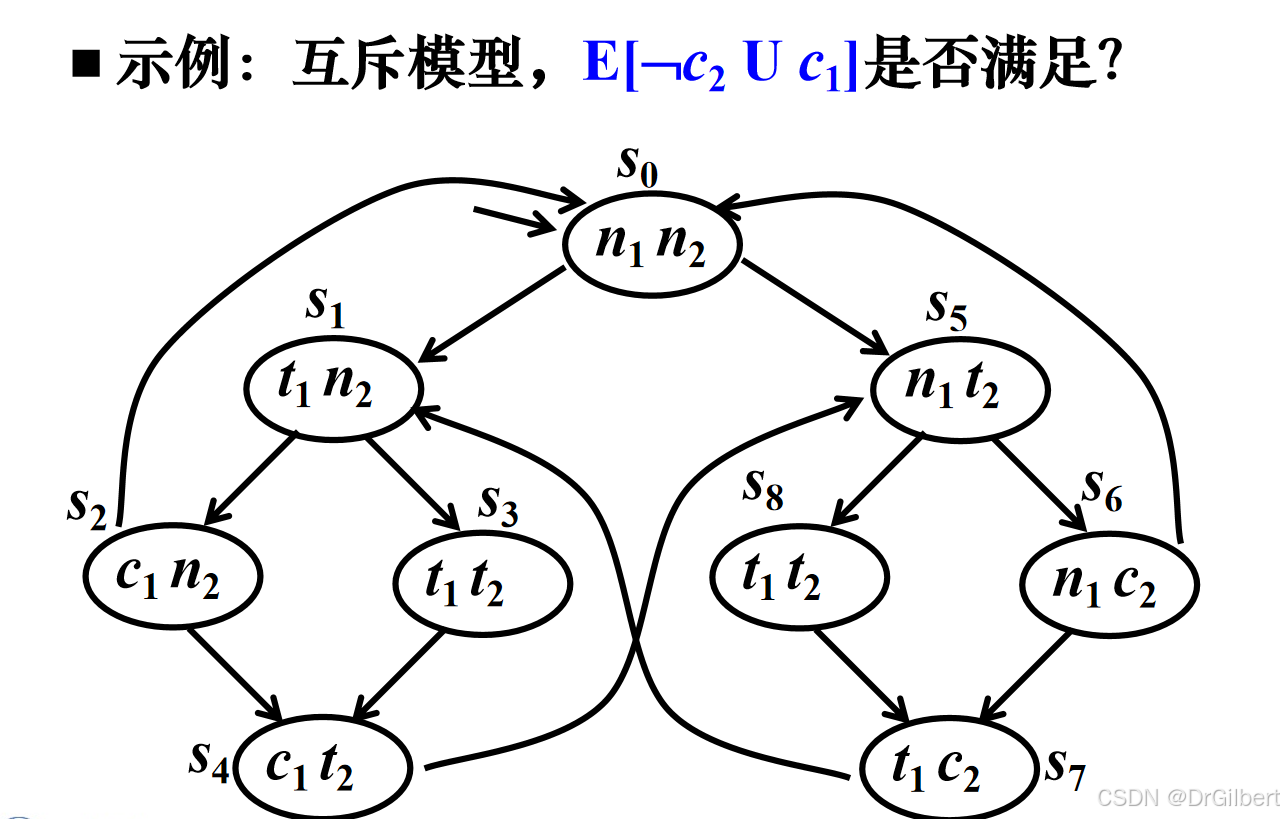
如图所示,为了验证E[¬
c
2
c_2
c2U
c
1
c_1
c1](直到
c
1
c_1
c1为真之前,¬
c
2
c_2
c2为真),先为找出所有包含
c
1
c_1
c1的状态
s
2
,
s
4
s_2,s_4
s2,s4,然后找到
¬
c
2
¬c_2
¬c2(不包含c_2)的状态(除
s
6
,
s
7
s_6,s_7
s6,s7以外全体)。逐个状态分析可以得到其成立。