理论课：C2W4.Word Embeddings with Neural Networks

Training the CBOW model

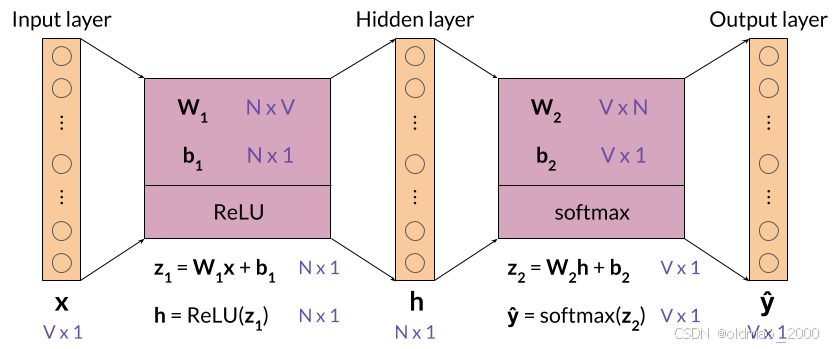
先根据网络构架搞清楚输出、隐藏层、输出维度

图中描述的是一个简单的神经网络模型，通常用于处理词嵌入（Word Embedding）任务，如连续词袋模型（Continuous Bag of Words, CBOW）。这个模型由输入层、隐藏层和输出层组成。下面是每个层和相关操作的维度解释：

1. 输入层 (Input layer):

   • 维度：$(N\times V)$
   • 描述：输入层接收一个词的one-hot编码，其中(N)是词汇表的大小，$(V)$是词汇表中每个词的向量维度（即one-hot编码的长度）。

2. 权重矩阵 W1 (Weight matrix W1):

   • 维度：$(N\times V)$到$ $(N\times 1)$
   • 描述：这是从输入层到隐藏层的权重矩阵。每个词的one-hot编码通过这个权重矩阵转换为隐藏层的激活值。

3. 偏置向量 b1 (Bias vector b1):

   • 维度：$(N\times 1)$
   • 描述：这是加在隐藏层激活值上的偏置项。

4. 隐藏层 (Hidden layer):

   • 维度：$(N\times 1)$
   • 描述：隐藏层的激活值由输入层的加权和加上偏置后通过激活函数（如ReLU）计算得到。

5. 激活函数 ReLU (Activation function ReLU):

   • 描述：隐藏层的激活函数，通常用于引入非线性，帮助模型学习复杂的模式。

6. 权重矩阵 W2 (Weight matrix W2):

   • 维度：$(V\times N)$
   • 描述：这是从隐藏层到输出层的权重矩阵。它将隐藏层的激活值转换为输出层的预测值。

7. 偏置向量 b2 (Bias vector b2):

   • 维度：$(V\times 1)$
   • 描述：这是加在输出层预测值上的偏置项。

8. 输出层 (Output layer):

   • 维度：$(V\times 1)$
   • 描述：输出层的值是模型对每个词的预测概率，通常通过softmax函数转换为概率分布。

9. softmax 函数:

   • 描述：softmax函数用于将输出层的线性预测值转换为概率分布，使得所有输出概率的和为1。

10. 预测值 $\hat{y}$ (Predicted value $\hat{y}$):

    • 描述：模型的最终输出，表示为每个词的概率。

这里将 $N$ 设为 3。$N$是 CBOW 模型的一个超参数，代表单词嵌入向量的大小以及隐藏层的大小。
$V$这里为5，是词表大小。

# Define the size of the word embedding vectors and save it in the variable 'N'
N = 3

# Define V. Remember this was the size of the vocabulary in the previous lecture notebooks
V = 5

Forward propagation

Initialization of the weights and biases

在开始训练CBOW 之前，需要用随机值初始化权重矩阵和偏置向量。正常是需要使用numpy.random.rand来完成该操作，这里直接填充好（大家实验结果才会一致，也可以用随机种子完成）：

# Define first matrix of weights
W1 = np.array([[ 0.41687358,  0.08854191, -0.23495225,  0.28320538,  0.41800106],
               [ 0.32735501,  0.22795148, -0.23951958,  0.4117634 , -0.23924344],
               [ 0.26637602, -0.23846886, -0.37770863, -0.11399446,  0.34008124]])

# Define second matrix of weights
W2 = np.array([[-0.22182064, -0.43008631,  0.13310965],
               [ 0.08476603,  0.08123194,  0.1772054 ],
               [ 0.1871551 , -0.06107263, -0.1790735 ],
               [ 0.07055222, -0.02015138,  0.36107434],
               [ 0.33480474, -0.39423389, -0.43959196]])

# Define first vector of biases
b1 = np.array([[ 0.09688219],
               [ 0.29239497],
               [-0.27364426]])

# Define second vector of biases
b2 = np.array([[ 0.0352008 ],
               [-0.36393384],
               [-0.12775555],
               [-0.34802326],
               [-0.07017815]])

检查参数的维度：

print(f'V (vocabulary size): {V}')
print(f'N (embedding size / size of the hidden layer): {N}')
print(f'size of W1: {W1.shape} (NxV)')
print(f'size of b1: {b1.shape} (Nx1)')
print(f'size of W2: {W2.shape} (VxN)')
print(f'size of b2: {b2.shape} (Vx1)')

结果：
V (vocabulary size): 5
N (embedding size / size of the hidden layer): 3
size of W1: (3, 5) (NxV)
size of b1: (3, 1) (Nx1)
size of W2: (5, 3) (VxN)
size of b2: (5, 1) (Vx1)
然后使用Part1中创建的一系列函数完成相关数据预处理操作：

# Define the tokenized version of the corpus
words = ['i', 'am', 'happy', 'because', 'i', 'am', 'learning']

# Get 'word2Ind' and 'Ind2word' dictionaries for the tokenized corpus
word2Ind, Ind2word = get_dict(words)

# Define the 'get_windows' function as seen in a previous notebook
def get_windows(words, C):
    i = C
    while i < len(words) - C:
        center_word = words[i]
        context_words = words[(i - C):i] + words[(i+1):(i+C+1)]
        yield context_words, center_word
        i += 1

# Define the 'word_to_one_hot_vector' function as seen in a previous notebook
def word_to_one_hot_vector(word, word2Ind, V):
    one_hot_vector = np.zeros(V)
    one_hot_vector[word2Ind[word]] = 1
    return one_hot_vector

# Define the 'context_words_to_vector' function as seen in a previous notebook
def context_words_to_vector(context_words, word2Ind, V):
    context_words_vectors = [word_to_one_hot_vector(w, word2Ind, V) for w in context_words]
    context_words_vectors = np.mean(context_words_vectors, axis=0)
    return context_words_vectors

# Define the generator function 'get_training_example' as seen in a previous notebook
def get_training_example(words, C, word2Ind, V):
    for context_words, center_word in get_windows(words, C):
        yield context_words_to_vector(context_words, word2Ind, V), word_to_one_hot_vector(center_word, word2Ind, V)

Training example

# Save generator object in the 'training_examples' variable with the desired arguments
training_examples = get_training_example(words, 2, word2Ind, V)

使用 yield 关键字的 get_training_examples 被称为生成器。运行时，它会生成一个迭代器（iterator），迭代器是一种特殊类型的对象…你可以对它进行迭代（例如使用 for 循环），以检索函数生成的连续值。
在这种情况下，get_training_examples会生成训练示例，对training_examples进行迭代会返回连续的训练示例。
下面取出生成器的第一个值：

# Get first values from generator
x_array, y_array = next(training_examples)

next 是另一个特殊的关键字，用于从迭代器中获取下一个可用值。上面的代码你会得到第一个值，也就是第一个训练示例。如果再次运行这个单元，就会得到下一个值，依此类推，直到迭代器返回的值用完为止。
这里使用 next 是因为只进行一次迭代训练，如果在多个迭代中进行完整的训练，需要使用常规的 for 循环以提供训练示例的迭代器。

打印提取到的向量：

# Print context words vector
x_array

结果：array([0.25, 0.25, 0. , 0.5 , 0. ])

# Print one hot vector of center word
y_array

结果：array([0., 0., 1., 0., 0.])
现在将这些向量转换为矩阵（或二维数组），以便能够在正确类型的对象上执行矩阵乘法

# Copy vector
x = x_array.copy()

# Reshape it
x.shape = (V, 1)

# Print it
print(f'x:\n{x}\n')

# Copy vector
y = y_array.copy()

# Reshape it
y.shape = (V, 1)

# Print it
print(f'y:\n{y}')

结果：

x:
[[0.25]
 [0.25]
 [0.  ]
 [0.5 ]
 [0.  ]]

y:
[[0.]
 [0.]
 [1.]
 [0.]
 [0.]]

定义激活函数：

# Define the 'relu' function as seen in the previous lecture notebook
def relu(z):
    result = z.copy()
    result[result < 0] = 0
    return result

# Define the 'softmax' function as seen in the previous lecture notebook
def softmax(z):
    e_z = np.exp(z)
    sum_e_z = np.sum(e_z)
    return e_z / sum_e_z

Values of the hidden layer

初始化完毕前向传播所需的所有变量，可以使用下面的公式计算隐藏层的值：
$$\begin{array}{r}{\mathbf{z}}_1={\mathbf{W}}_1\mathbf{x}+{\mathbf{b}}_1\\ \mathbf{h}=\mathrm{ReLU}({\mathbf{z}}_1)\end{array}\text{\hspace{1em}(1)(2)}$$
根据公式1写代码：

# Compute z1 (values of first hidden layer before applying the ReLU function)
z1 = np.dot(W1, x) + b1
# Print z1
z1

结果：

array([[ 0.36483875],
       [ 0.63710329],
       [-0.3236647 ]])

根据公式2写代码：

# Compute h (z1 after applying ReLU function)
h = relu(z1)

# Print h
h

结果：

array([[0.36483875],
       [0.63710329],
       [0.        ]])

注意观察，上面是ReLU的结果。

Values of the output layer

以下是计算输出层（以向量 $\hat{y}$表示）值所需的公式：
$$\begin{array}{rl}{\mathbf{z}}_2& ={\mathbf{W}}_2\mathbf{h}+{\mathbf{b}}_2\\ \hat{\mathbf{y}}& =\mathrm{softmax}({\mathbf{z}}_2)\end{array}\text{\hspace{1em}(3)(4)}$$
根据公式3写代码：

# Compute z2 (values of the output layer before applying the softmax function)
z2 = np.dot(W2, h) + b2

# Print z2
z2

结果：

array([[-0.31973737],
       [-0.28125477],
       [-0.09838369],
       [-0.33512159],
       [-0.19919612]])

注意其维度是：$(V\times 1)$
根据公式4计算输出：

# Compute y_hat (z2 after applying softmax function)
y_hat = softmax(z2)

# Print y_hat
y_hat

结果：

array([[0.18519074],
       [0.19245626],
       [0.23107446],
       [0.18236353],
       [0.20891502]])

思考：得到了输出$\hat{y}$，如何计算其预测的单词 ¹？

Cross-entropy loss

有了预测结果，就可以计算Cross-entropy损失来决定预测的准确度有多少。
这里因为只有一个训练样本，而非一个batch的训练样本，因此用lost，不是cost。当然，cost是lost的一般形式。
再次打印预测结果和真实值：

# Print prediction
y_hat

结果：

array([[0.18519074],
       [0.19245626],
       [0.23107446],
       [0.18236353],
       [0.20891502]])

# Print target value
y

结果：

array([[0.],
       [0.],
       [1.],
       [0.],
       [0.]])

交叉熵损失计算公式为：

$$J=-\sum _{k=1}^V{y}_k\log {\hat{y}}_k\text{\hspace{1em}(6)}$$
对应的代码为：

def cross_entropy_loss(y_predicted, y_actual):
    # Fill the loss variable with your code
    loss = np.sum(-np.log(y_hat)*y)
    return loss

测试：

# Print value of cross entropy loss for prediction and target value
cross_entropy_loss(y_hat, y)

结果：1.4650152923611106
这个结果不好也不坏，模型还没学习到任何信息，需要继续进行反向传播

Backpropagation

根据网络构架，反向传播用到的公式为：
$$\begin{array}{rl}\frac{\partial J}{\partial {\mathbf{W}}_1}& =\mathrm{ReLU}\left({\mathbf{W}}_2^{\top }(\hat{\mathbf{y}}-\mathbf{y})\right){\mathbf{x}}^{\top }\\ \frac{\partial J}{\partial {\mathbf{W}}_2}& =(\hat{\mathbf{y}}-\mathbf{y}){\mathbf{h}}^{\top }\\ \frac{\partial J}{\partial {\mathbf{b}}_1}& =\mathrm{ReLU}\left({\mathbf{W}}_2^{\top }(\hat{\mathbf{y}}-\mathbf{y})\right)\\ \frac{\partial J}{\partial {\mathbf{b}}_2}& =\hat{\mathbf{y}}-\mathbf{y}\end{array}\text{\hspace{1em}(7)(8)(9)(10)}$$
以上公式是针对单个样本的，batch操作会更复杂，先计算公式10

# Compute vector with partial derivatives of loss function with respect to b2
grad_b2 = y_hat - y

# Print this vector
grad_b2

结果：

array([[ 0.18519074],
       [ 0.19245626],
       [-0.76892554],
       [ 0.18236353],
       [ 0.20891502]])

然后根据公式8写代码：

# Compute matrix with partial derivatives of loss function with respect to W2
grad_W2 = np.dot(y_hat - y, h.T)

# Print matrix
grad_W2

结果：

array([[ 0.06756476,  0.11798563,  0.        ],
       [ 0.0702155 ,  0.12261452,  0.        ],
       [-0.28053384, -0.48988499, -0.        ],
       [ 0.06653328,  0.1161844 ,  0.        ],
       [ 0.07622029,  0.13310045,  0.        ]])

按公式9写代码：

# Compute vector with partial derivatives of loss function with respect to b1
grad_b1 = relu(np.dot(W2.T, y_hat - y))

# Print vector
grad_b1

结果：

array([[0.        ],
       [0.        ],
       [0.17045858]])

最后计算公式7：

# Compute matrix with partial derivatives of loss function with respect to W1
grad_W1 = np.dot(relu(np.dot(W2.T, y_hat - y)), x.T)

# Print matrix
grad_W1

结果：

array([[0.        , 0.        , 0.        , 0.        , 0.        ],
       [0.        , 0.        , 0.        , 0.        , 0.        ],
       [0.04261464, 0.04261464, 0.        , 0.08522929, 0.        ]])

再次确认结果的维度：

print(f'V (vocabulary size): {V}')
print(f'N (embedding size / size of the hidden layer): {N}')
print(f'size of grad_W1: {grad_W1.shape} (NxV)')
print(f'size of grad_b1: {grad_b1.shape} (Nx1)')
print(f'size of grad_W2: {grad_W2.shape} (VxN)')
print(f'size of grad_b2: {grad_b2.shape} (Vx1)')

结果：
V (vocabulary size): 5
N (embedding size / size of the hidden layer): 3
size of grad_W1: (3, 5) (NxV)
size of grad_b1: (3, 1) (Nx1)
size of grad_W2: (5, 3) (VxN)
size of grad_b2: (5, 1) (Vx1)

Gradient descent

在梯度下降阶段，可使用下面的公式从原始矩阵和向量中减去 $\alpha$ 乘以梯度来更新权重和偏置。
$$\begin{array}{rl}{\mathbf{W}}_1& :={\mathbf{W}}_1-\alpha \frac{\partial J}{\partial {\mathbf{W}}_1}\\ {\mathbf{W}}_2& :={\mathbf{W}}_2-\alpha \frac{\partial J}{\partial {\mathbf{W}}_2}\\ {\mathbf{b}}_1& :={\mathbf{b}}_1-\alpha \frac{\partial J}{\partial {\mathbf{b}}_1}\\ {\mathbf{b}}_2& :={\mathbf{b}}_2-\alpha \frac{\partial J}{\partial {\mathbf{b}}_2}\end{array}\text{\hspace{1em}(11)(12)(13)(14)}$$
先给超参数一个初始值：

# Define alpha
alpha = 0.03

先按公式11计算：

# Compute updated W1
W1_new = W1 - alpha * grad_W1

比较更新前后的值：

print('old value of W1:')
print(W1)
print()
print('new value of W1:')
print(W1_new)

结果：

old value of W1:
[[ 0.41687358  0.08854191 -0.23495225  0.28320538  0.41800106]
 [ 0.32735501  0.22795148 -0.23951958  0.4117634  -0.23924344]
 [ 0.26637602 -0.23846886 -0.37770863 -0.11399446  0.34008124]]

new value of W1:
[[ 0.41687358  0.08854191 -0.23495225  0.28320538  0.41800106]
 [ 0.32735501  0.22795148 -0.23951958  0.4117634  -0.23924344]
 [ 0.26509758 -0.2397473  -0.37770863 -0.11655134  0.34008124]]

根据公式12.13.14更新其他三个参数：

# Compute updated W2
W2_new = W2 - alpha * grad_W2

# Compute updated b1
b1_new = b1 - alpha * grad_b1

# Compute updated b2
b2_new = b2 - alpha * grad_b2


print('W2_new')
print(W2_new)
print()
print('b1_new')
print(b1_new)
print()
print('b2_new')
print(b2_new)

结果：

W2_new
[[-0.22384758 -0.43362588  0.13310965]
 [ 0.08265956  0.0775535   0.1772054 ]
 [ 0.19557112 -0.04637608 -0.1790735 ]
 [ 0.06855622 -0.02363691  0.36107434]
 [ 0.33251813 -0.3982269  -0.43959196]]

b1_new
[[ 0.09688219]
 [ 0.29239497]
 [-0.27875802]]

b2_new
[[ 0.02964508]
 [-0.36970753]
 [-0.10468778]
 [-0.35349417]
 [-0.0764456 ]]

Extracting word embedding vectors

开始前，把CBOW训练好的参数都重新给一次：

import numpy as np
from utils2 import get_dict

# Define the tokenized version of the corpus
words = ['i', 'am', 'happy', 'because', 'i', 'am', 'learning']

# Define V. Remember this is the size of the vocabulary
V = 5

# Get 'word2Ind' and 'Ind2word' dictionaries for the tokenized corpus
word2Ind, Ind2word = get_dict(words)


# Define first matrix of weights
W1 = np.array([[ 0.41687358,  0.08854191, -0.23495225,  0.28320538,  0.41800106],
               [ 0.32735501,  0.22795148, -0.23951958,  0.4117634 , -0.23924344],
               [ 0.26637602, -0.23846886, -0.37770863, -0.11399446,  0.34008124]])

# Define second matrix of weights
W2 = np.array([[-0.22182064, -0.43008631,  0.13310965],
               [ 0.08476603,  0.08123194,  0.1772054 ],
               [ 0.1871551 , -0.06107263, -0.1790735 ],
               [ 0.07055222, -0.02015138,  0.36107434],
               [ 0.33480474, -0.39423389, -0.43959196]])

# Define first vector of biases
b1 = np.array([[ 0.09688219],
               [ 0.29239497],
               [-0.27364426]])

# Define second vector of biases
b2 = np.array([[ 0.0352008 ],
               [-0.36393384],
               [-0.12775555],
               [-0.34802326],
               [-0.07017815]])

一共有三种提取词向量的方式。

Option 1: extract embedding vectors from ${\mathbf{W}}_1$

观察参数${\mathbf{W}}_1$，这个矩阵的第一列（3个元素）对应第一个单词的表征，第二列对应第二个单词，以此类推。我们把词库里面的单词按index打印出来：

# Print corresponding word for each index within vocabulary's range
for i in range(V):
    print(Ind2word[i])

结果：
am
because
happy
i
learning
将参数${\mathbf{W}}_1$对应单词的表征提取出来：

# Loop through each word of the vocabulary
for word in word2Ind:
    # Extract the column corresponding to the index of the word in the vocabulary
    word_embedding_vector = W1[:, word2Ind[word]]
    # Print word alongside word embedding vector
    print(f'{word}: {word_embedding_vector}')

结果：
am: [0.41687358 0.32735501 0.26637602]
because: [ 0.08854191 0.22795148 -0.23846886]
happy: [-0.23495225 -0.23951958 -0.37770863]
i: [ 0.28320538 0.4117634 -0.11399446]
learning: [ 0.41800106 -0.23924344 0.34008124]

Option 2: extract embedding vectors from ${\mathbf{W}}_2$

第二个选择是使用 ${\mathbf{W}}_2$的转置来提取单词的表征，先看${\mathbf{W}}_2$的转置：

# Print transposed W2
W2.T

结果：

array([[-0.22182064,  0.08476603,  0.1871551 ,  0.07055222,  0.33480474],
       [-0.43008631,  0.08123194, -0.06107263, -0.02015138, -0.39423389],
       [ 0.13310965,  0.1772054 , -0.1790735 ,  0.36107434, -0.43959196]])

将单词和其表征打印出来：

# Loop through each word of the vocabulary
for word in word2Ind:
    # Extract the column corresponding to the index of the word in the vocabulary
    word_embedding_vector = W2.T[:, word2Ind[word]]
    # Print word alongside word embedding vector
    print(f'{word}: {word_embedding_vector}')

结果：

am: [-0.22182064 -0.43008631  0.13310965]
because: [0.08476603 0.08123194 0.1772054 ]
happy: [ 0.1871551  -0.06107263 -0.1790735 ]
i: [ 0.07055222 -0.02015138  0.36107434]
learning: [ 0.33480474 -0.39423389 -0.43959196]

Option 3: extract embedding vectors from ${\mathbf{W}}_1$ and ${\mathbf{W}}_2$

将前面两种方法结合到一起，计算${\mathbf{W}}_1$ 和 ${\mathbf{W}}_2^{\top }$的平均，得到W3：

# Compute W3 as the average of W1 and W2 transposed
W3 = (W1+W2.T)/2

# Print W3
W3

结果：

array([[ 0.09752647,  0.08665397, -0.02389858,  0.1768788 ,  0.3764029 ],
       [-0.05136565,  0.15459171, -0.15029611,  0.19580601, -0.31673866],
       [ 0.19974284, -0.03063173, -0.27839106,  0.12353994, -0.04975536]])

打印单词表征结果：

# Loop through each word of the vocabulary
for word in word2Ind:
    # Extract the column corresponding to the index of the word in the vocabulary
    word_embedding_vector = W3[:, word2Ind[word]]
    # Print word alongside word embedding vector
    print(f'{word}: {word_embedding_vector}')

结果：

am: [ 0.09752647 -0.05136565  0.19974284]
because: [ 0.08665397  0.15459171 -0.03063173]
happy: [-0.02389858 -0.15029611 -0.27839106]
i: [0.1768788  0.19580601 0.12353994]
learning: [ 0.3764029  -0.31673866 -0.04975536]