2.8 线性表的归并

归并: 把两个表或多个表按照某种策略(规则)合并成一个表. 例如以后要介绍的归并排序就是归并的一个应用. 在线性表这一章, 我们只介绍二路归并. 即把两个线性表合并成一个表. 归并规则是把两个已经有序的线性表给归并成一个更长的线性表, 得到的表也是有序的.

1. 顺序表归并

策略: 每次从两个顺序表中挑出最小的元素, 然后把它插入到当前所归并好的那一段的顺序表的末端即可. 两个原始的顺序表均有序, 需要另外开辟存储空间来存储归并后的顺序表.

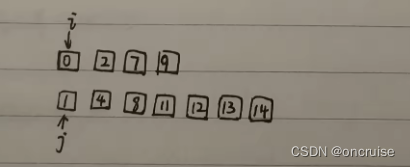
图1. 顺序表的归并

如图, 上面的顺序表记为a[ ], 长度为m; 下面的顺序表记为b[ ], 长度为n; 用c[ ] 存储归并后的顺序表. k记录c[ ] 中当前要放入的元素的索引. 怎么归并? 需要分别比较a[ i ]和b[ j ]的值, 将较小者放入c[ k ]中, 然后k++; 较小者的索引自增1; 比如若a[ i ] <b[ j ], 则c[ k ] = a[ i ]; k++; i++; 反之则c[ k ] = b[ j ]; k++; j++; 循环的判断条件该怎么写? 每次循环都会导致 i 或者 j 自增1, 这样总会有一个顺序表先遍历完, 需要注意的是, 并不是短的顺序表就一定先遍历结束, 因为 i 或 j 的自增是有条件的. 假如a比较短, 但a中所有的元素都大于b中的元素, 则归并的时候肯定是b中的元素先被归并到c[ ] 中, 也即b[ ] 先被遍历完. 只要有一个表被遍历完, 则说明另一个未遍历完的表中的元素, 全部大于归并好的元素, 这时只需要将未归并的元素依次放入c[ ] 中即可.

#include <iostream>

/// <summary>
/// 数组最大长度
/// </summary>
const int MAX_SIZE = 10;

/// <summary>
/// 顺序表的归并
/// </summary>
/// <param name="a">有序的顺序表1</param>
/// <param name="m">顺序表1的长度</param>
/// <param name="b">有序的顺序表2</param>
/// <param name="n">顺序表2的长度</param>
/// <param name="c">归并后的顺序表</param>
/// <param name="k">归并后的顺序表的长度</param>
void mergeArray(int* a, int m, int* b, int n, int* c, int& k) {		//假设传入的数组c长度足够大
	int i = 0;
	int j = 0;

	int compTimes = 0;		//比较次数

	while (i < m && j < n) {
		if (a[i] < b[j]) {
			c[k] = a[i];
			k++;
			i++;
		}
		else {
			c[k] = b[j];
			k++;
			j++;
		}
		compTimes++;
	}

	while (i < m) {		//下面这两个循环只会执行其中一个
		c[k] = a[i];
		k++;
		i++;
	}
	while (j < n) {
		c[k] = b[j];
		k++;
		j++;
	}

	printf("比较次数: %d\n", compTimes);
}

int main()
{
	int a[MAX_SIZE] = { 0, 2, 7, 9 };
	int m = 4;

	int b[MAX_SIZE] = { 1, 4, 8, 11, 12, 13, 14 };
	int n = 7;

	int c[MAX_SIZE * 2] = {};
	int k = 0;

	mergeArray(a, m, b, n, c, k);

	printf("归并后的顺序表长度: %d\n", k);
	printf("归并后的顺序表元素: \n");
	for (int i = 0; i < k; i++)
	{
		printf("%d\n", c[i]);
	}
}

代码1: 顺序表的归并

现在我们研究一下顺序表归并的比较次数. 可以看出只有在第一个while循环里面才会进行比较.

什么情况下比较次数最少? 由于第一个while循环会至少遍历完其中的一个顺序表, 因此比较次数最少为min{m, n}, 这种情况下, 索引 i 和 j 只能有一个发生了移动, 另一个索引始终指向顺序表的第一个元素. 也即当其中一个顺序表的所有元素全部大于另一个顺序表中的所有元素的时候, 比较的次数最少, 为min{m, n};

什么情况下比较次数最多? 显然是遍历过程中, 索引 i 和 j 全部发生了移动, 也即 i 和 j 最后都指向了顺序表的最后一个元素. 若 a = {7, 8, 9, 10}; m为4; b = {1, 2, 3, 4, 5, 6, 9999}; n为7; 则 j 先从0变化到5, 比较了6次, i 再从0变化到3, 比较了4次, 此时a已经遍历完毕, 跳出循环. 共比较了6 + 4 = 10次. 即m + n - 1次. 也即遍历过程中, 其中一个表b的索引先移动到最后一个元素, 此时比较的次数为该表b的表长 - 1, 即n - 1. 然后另外一个表a的索引移动到该表的最后一个元素, 此时又比较了表a的表长的次数, 即m. 此时表a遍历完毕, 跳出循环. 故最坏的情况需要比较m + n - 1次.

2. 链表归并

1. 尾插法归并链表

图2. 尾插法归并链表

如图, 归并A, B两个升序的链表, 将其归并到链表C中. p指向A中待归并的结点, q指向B中待归并的结点, r指向C中已归并的结点. 同时对链表A和链表B进行遍历, 当p != NULL && q != NULL时进行循环, 比较两个链表中结点的值, 若p->data < q->data, 则r->next = p; p = p->next; r = r->next; 反之, 则r->next = q; q = q->next; r = r->next; 循环结束后, 若p != NULL; 则r->next = p; 若q != NULL; 则r->next = q; 尾插法归并链表得到的链表是顺序的.

#include <iostream>

/// <summary>
/// 链表结点结构体定义
/// </summary>
typedef struct LNode {
	int data;
	struct LNode* next;
}LNode;

/// <summary>
/// 尾插法归并单链表
/// </summary>
/// <param name="A"></param>
/// <param name="B"></param>
/// <param name="C"></param>
void merge(LNode* A, LNode* B, LNode* C) {	
	LNode* p = A->next;		//p指向A中待归并的结点
	LNode* q = B->next;		//q指向B中待归并的结点
	LNode* r = C;			//r指向C中已归并的结点
	C->next = NULL;
	free(A);
	free(B);

	while (p != NULL && q != NULL)
	{
		if (p->data < q->data) {
			r->next = p;
			p = p->next;
			r = r->next;
		}
		else {
			r->next = q;
			q = q->next;
			r = r->next;
		}
	}

	if (p != NULL) {
		r->next = p;
	}
	if (q != NULL) {
		r->next = q;
	}
}

int main()
{
	LNode* A = (LNode*)malloc(sizeof(LNode));
	LNode* a0 = (LNode*)malloc(sizeof(LNode));
	LNode* a1 = (LNode*)malloc(sizeof(LNode));
	LNode* a2 = (LNode*)malloc(sizeof(LNode));
	LNode* a3 = (LNode*)malloc(sizeof(LNode));

	A->data = NULL;
	a0->data = 0; 
	a1->data = 2;
	a2->data = 7;
	a3->data = 9;

	A->next = a0;
	a0->next = a1;
	a1->next = a2;
	a2->next = a3;
	a3->next = NULL;

	LNode* B = (LNode*)malloc(sizeof(LNode));
	LNode* b0 = (LNode*)malloc(sizeof(LNode));
	LNode* b1 = (LNode*)malloc(sizeof(LNode));
	LNode* b2 = (LNode*)malloc(sizeof(LNode));
	LNode* b3 = (LNode*)malloc(sizeof(LNode));
	LNode* b4 = (LNode*)malloc(sizeof(LNode));
	LNode* b5 = (LNode*)malloc(sizeof(LNode));
	LNode* b6 = (LNode*)malloc(sizeof(LNode));

	B->data = NULL;
	b0->data = 1;
	b1->data = 4;
	b2->data = 8;
	b3->data = 11;
	b4->data = 12;
	b5->data = 13;
	b6->data = 15;

	B->next = b0;
	b0->next = b1;
	b1->next = b2;
	b2->next = b3;
	b3->next = b4;
	b4->next = b5;
	b5->next = b6;
	b6->next = NULL;

	LNode* C = (LNode*)malloc(sizeof(LNode));

	merge(A, B, C);

	LNode* p = C->next;
	printf("归并后的数据: \n");
	while (p != NULL)
	{
		printf("%d\n", p->data);
		p = p->next;
	}
}

代码2: 链表的尾插法归并

/// <summary>
/// 尾插法归并单链表
/// </summary>
/// <param name="A"></param>
/// <param name="B"></param>
/// <param name="C"></param>
void merge(LNode* A, LNode* B, LNode* C) {	
	LNode* p = A->next;		//p指向A中待归并的结点
	LNode* q = B->next;		//q指向B中待归并的结点
	LNode* r = C;			//r指向C中已归并的结点
	C->next = NULL;
	free(A);
	free(B);

	while (p != NULL && q != NULL)
	{
		if (p->data < q->data) {
			r->next = p;
			p = p->next;
			r = r->next;
		}
		else {
			r->next = q;
			q = q->next;
			r = r->next;
		}
	}

	if (p != NULL) {
		r->next = p;
	}
	if (q != NULL) {
		r->next = q;
	}
}

代码3: 尾插法归并链表核心代码

2. 头插法归并链表

图3. 头插法归并链表

如图, 归并A, B两个升序的链表, 将其归并到链表C中. p指向A中待归并的结点, q指向B中待归并的结点. C作为头结点, 接收插入的元素, 将插入的元素放在C的后面. s指向当前取出的最小值结点. 同时对链表A和链表B进行遍历, 当p != NULL && q != NULL时进行循环, 若p->data < q->data; 则s = p; p = p->next; s->next = C->next; C->next = s; 反之, 则s = q; q = q->next; s->next = C->next; C->next = s; 循环结束后, 当p != NULL时; 则重复之前的操作, 即s = p; p = p->next; s->next = C->next; C->next = s; 当q != NULL时; 则重复之前的操作, 即s = q; q = q->next; s->next = C->next; C->next = s; 头插法归并链表得到的链表是顺序的.

#include <iostream>

/// <summary>
/// 链表结点结构体定义
/// </summary>
typedef struct LNode {
	int data;
	struct LNode* next;
}LNode;

/// <summary>
/// 头插法归并单链表
/// </summary>
/// <param name="A"></param>
/// <param name="B"></param>
/// <param name="C"></param>
void merge(LNode* A, LNode* B, LNode* C) {	
	LNode* p = A->next;		//p指向A中待归并的结点
	LNode* q = B->next;		//q指向B中待归并的结点
	LNode* s;				//s指向当前取出的最小值结点
	C->next = NULL;
	free(A);
	free(B);

	while (p != NULL && q != NULL)
	{
		if (p->data < q->data) {
			s = p;
			p = p->next;
			s->next = C->next;
			C->next = s;
		}
		else {
			s = q;
			q = q->next;
			s->next = C->next;
			C->next = s;
		}
	}

	while (p != NULL) {
		s = p;
		p = p->next;
		s->next = C->next;
		C->next = s;
	}
	while (q != NULL)
	{
		s = q;
		q = q->next;
		s->next = C->next;
		C->next = s;
	}
}

int main()
{
	LNode* A = (LNode*)malloc(sizeof(LNode));
	LNode* a0 = (LNode*)malloc(sizeof(LNode));
	LNode* a1 = (LNode*)malloc(sizeof(LNode));
	LNode* a2 = (LNode*)malloc(sizeof(LNode));
	LNode* a3 = (LNode*)malloc(sizeof(LNode));

	A->data = NULL;
	a0->data = 0; 
	a1->data = 2;
	a2->data = 7;
	a3->data = 9;

	A->next = a0;
	a0->next = a1;
	a1->next = a2;
	a2->next = a3;
	a3->next = NULL;

	LNode* B = (LNode*)malloc(sizeof(LNode));
	LNode* b0 = (LNode*)malloc(sizeof(LNode));
	LNode* b1 = (LNode*)malloc(sizeof(LNode));
	LNode* b2 = (LNode*)malloc(sizeof(LNode));
	LNode* b3 = (LNode*)malloc(sizeof(LNode));
	LNode* b4 = (LNode*)malloc(sizeof(LNode));
	LNode* b5 = (LNode*)malloc(sizeof(LNode));
	LNode* b6 = (LNode*)malloc(sizeof(LNode));

	B->data = NULL;
	b0->data = 1;
	b1->data = 4;
	b2->data = 8;
	b3->data = 11;
	b4->data = 12;
	b5->data = 13;
	b6->data = 15;

	B->next = b0;
	b0->next = b1;
	b1->next = b2;
	b2->next = b3;
	b3->next = b4;
	b4->next = b5;
	b5->next = b6;
	b6->next = NULL;

	LNode* C = (LNode*)malloc(sizeof(LNode));

	merge(A, B, C);

	LNode* p = C->next;
	printf("归并后的数据: \n");
	while (p != NULL)
	{
		printf("%d\n", p->data);
		p = p->next;
	}
}

代码4: 链表的头插法归并

/// <summary>
/// 头插法归并单链表
/// </summary>
/// <param name="A"></param>
/// <param name="B"></param>
/// <param name="C"></param>
void merge(LNode* A, LNode* B, LNode* C) {	
	LNode* p = A->next;		//p指向A中待归并的结点
	LNode* q = B->next;		//q指向B中待归并的结点
	LNode* s;				//s指向当前取出的最小值结点
	C->next = NULL;
	free(A);
	free(B);

	while (p != NULL && q != NULL)
	{
		if (p->data < q->data) {
			s = p;
			p = p->next;
			s->next = C->next;
			C->next = s;
		}
		else {
			s = q;
			q = q->next;
			s->next = C->next;
			C->next = s;
		}
	}

	while (p != NULL) {
		s = p;
		p = p->next;
		s->next = C->next;
		C->next = s;
	}
	while (q != NULL)
	{
		s = q;
		q = q->next;
		s->next = C->next;
		C->next = s;
	}
}

代码5: 头插法归并链表核心代码