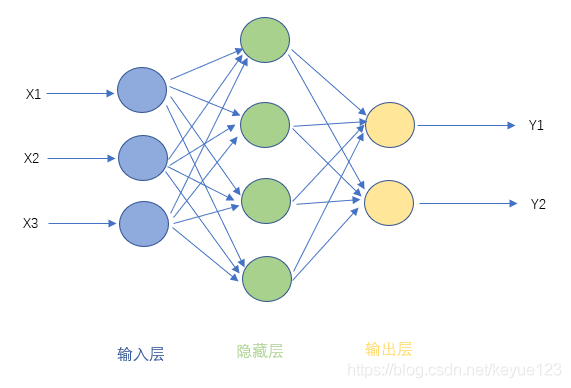
全连接神经网络
前馈神经网络
包含的层:
- 线性层和卷积层:这两种层对输入进行线性计算。层内维护着线性运算的权重
- 激活层:这层对数据进行非线性运算。非线性运算时可以逐元素非线性运算的,也可以是其它类习惯的非线性运算
- 归一化层:根据输入的均值和方差对数据进行归一化,使得数据的范围在一个相对固定的范围内
- 池化层和视觉层:这两种层和数据重采样有关,包括对数据进行下采样(就是隔几个数据采一个数据)、上采样(把一个数据复制出很多份)和重新排序。
- 丢弃层:在输入中随机选择一些输出
- 补齐层:采用循环补齐等方法让数据变多
一般的简单表示方式:
使用torch.nn.Sequential类搭建前馈神经网络
torch.nn.Sequential类是由torch.nn.Module类派生得到的。
torch.nn.Moudle类及其子类有以下用途。
- 表示一个神经网络 例如
torch.nn.Sequential类可以表示一个前馈神经网络 - 表示神经网络的一个层 例如上次说的
torch.nn.Linear就是表示神经网络的一个层的线性连接部分,它是一种线性层;torch.nn.ReLU类表示逐元素计算max(·, 0),它是一种激活层。 - 表示损失。
torch.nn.MSELoss类、torch.nn.L1Loss类、torch.nn.SmoothL1Loss类等等
from torch.nn import Linear, ReLU, Sequential
net = Sequential(Linear(3, 4), ReLU(), Linear(4, 2), ReLU())
print(net)
输出:
Sequential(
(0): Linear(in_features=3, out_features=4, bias=True)
(1): ReLU()
(2): Linear(in_features=4, out_features=2, bias=True)
(3): ReLU()
)
全连接层和全连接神经网络
全连接层的意思
所谓全连接层,就是指一个神经元组成的层所有输出和该层的所有输入都连接,即每个输入都会影响所有的神经元输出
注意:一般来说两个线性层之间可能会有一个激活层,例如ReLU之类的激活函数,这个计算是非线性的,如果,如果把它分开来看的话激活层可能就不算全连接层,但是一般情况下我们把线性函数和激活函数合起来看就行了。
全连接神经网络的意思
全连接神经网络是仅由全连接层组成的前馈神经网络。
全连接神经网络是一种特殊的前馈神经网络
非线性激活
非线性激活的必要性
如果一个神经网络没有激活层,所有运算都是线性计算,整个网络就是一个线性组合,这样的神经网络就发挥不出它的优势
激活层分为两大类
- 基于逐元素非线性运算的激活层。对于这类激活层,一个称为“激活函数”的非线性函数对张量进行逐元素运算。例如可以对张量求(x, max),或是逐元素求expit()。
- 多元素组合运算的激活层,对于这类激活层,并不是“激活函数”对张量逐元素运算,而是利用多个元素的值联合计算。例如对某些元素联合起来进行softmax()运算。
逐元素激活
分为三类:
- S形激活
- 单侧激活
- 皱缩激活
S型激活
S型激活函数把(-∞, +∞)范围的值映射到一个有限的闭区间里。从这个意义来看,S型激活可以有效控制输出的范围。但是S型激活函数常常在输入的绝对值比较大的时候导数为零,从而导致梯度消失
| 激活函数 | 值域 | torch.nn.Modul的子类 |
|---|---|---|
| s o f t z = z 1 + ∥ z ∥ soft z = {z \over {1+\|z\|}} softz=1+∥z∥z | (-1, 1) | torch.nn.Softsign |
| e x p i t z = 1 1 + e x p ( − z ) expitz = {1 \over {1+exp(-z)}} expitz=1+exp(−z)1 | (0, 1) | torch.nn.Sigmoid |
| t a n h z = e x p ( z ) − e x p ( − z ) e x p ( z ) + e x p ( − z ) tanh z = {exp(z) - exp(-z) \over {exp(z) + exp(-z)}} tanhz=exp(z)+exp(−z)exp(z)−exp(−z) | (-1, 1) | torch.nn.Hardtanh |
| h a r d t a n h z = { 1 , z > 1 z , − 1 ≤ z ≤ 1 − 1 , z > 6 hardtanh z = \begin{cases} 1, & z > 1 \\ z, & -1 \leq z \leq 1 \\ -1, & z > 6 \end{cases} hardtanhz=⎩⎪⎨⎪⎧1,z,−1,z>1−1≤z≤1z>6 | [-1, 1] | torch.nn.Hardtanh |
| r e l u 6 z = { 0 , z < 0 z , 0 ≤ z ≤ 6 6 , z > 6 relu6 z = \begin{cases} 0, & z < 0 \\ z, & 0 \leq z \leq 6 \\ 6, & z > 6 \end{cases} relu6z=⎩⎪⎨⎪⎧0,z,6,z<00≤z≤6z>6 | [0, 6] | torch.nn.ReLU6 |
它们的图像在经过放缩和平移之后完全一样。对自变量的的放缩和平移往往可以通过放缩和偏移之前层的权重抵消,上面这几个函数的主要区别为输出范围不同。
单侧激活函数
单侧激活函数一般是把(-∞, +∞)映射到(c, +∞)(有例外),采用这种激活函数后,比较大的值基本不变,而比较小的值就基本被抛弃了。这样的做法能够让比较多的输入有梯度,大大缓解了梯度消失的问题。但是它并不能完全将输出控制在一个范围内,并且会让输出的均值不为0,另外,这样的函数往往是通过分段实现的,从数学意义上来看在分段点上可能没有导数,这回引起不便。
Pytorch提供的单侧激活函数:
| 激活函数 | 值域 | torch.nn.Modul的子类 |
|---|---|---|
| r e l u z = { 0 , z < 0 z , z ≥ 0 relu z = \begin{cases} 0, & z < 0 \\ z, & z \geq 0 \end{cases} reluz={0,z,z<0z≥0 | [0, +∞) | torch.nn.ReLU |
| l e a k y r e l u ( z ; a ) = { a z , z < 0 z , z ≥ 0 leakyrelu (z; a) = \begin{cases} az, & z < 0 \\ z, & z \geq 0 \end{cases} leakyrelu(z;a)={az,z,z<0z≥0 | (-∞, +∞) | torch.nn.LeakyReLUtorch.nn.RReLUtorch.nn.PReLU |
| t h r e s h o l d ( z ; λ , ν ) = { ν , z < λ z , z ≥ λ threshold(z; \lambda, \nu) = \begin{cases} \nu, & z < \lambda \\ z, & z \geq \lambda \end{cases} threshold(z;λ,ν)={ν,z,z<λz≥λ | { ν } \{\nu\} {ν} ⋃ \bigcup ⋃ [ λ , + ∞ \lambda, +∞ λ,+∞ ) | torch.nn.Threshold |
| s e l u ( z ; σ , α ) = { σ α ( e x p ( z ) − 1 ) , z < 0 σ z , z ≥ 0 selu (z;\sigma, \alpha) = \begin{cases} \sigma\alpha(exp(z)-1), & z < 0 \\ \sigma z, & z \geq 0 \end{cases} selu(z;σ,α)={σα(exp(z)−1),σz,z<0z≥0 | [- $ \sigma\alpha $ , +∞) | torch.nn.ELUtorch.nn.SELU |
| s o f t p l u s ( z ; β ) = 1 β l n ( 1 + e x p ( β z ) ) softplus (z;\beta) = {{1 \over \beta} ln(1 + exp(\beta z))} softplus(z;β)=β1ln(1+exp(βz)) | (0, +∞) | torch.nn.Softplus |
| $ln expit(z) = -ln(1+exp(-z)) $ | (-∞, 0) | torch.nn.LogSigmoid |
基于斜坡函数relu()函数的激活层是最基本的激活层,但是这个激活层有一个明显的缺陷:它对负输入的输出为常数,这会导致很大范围内没有导数,很可能会严重的影响权重的求解。为了解决这个问题,Leaky ReLU、PReLU和RReLU。这三种激活在负输入的时候还有一个小的正导数α*(0 < α < 1),起到压缩功能,他们的区别如下:
- Leaky ReLU:构造类实例的时候需要传入α的值,一旦传入,不可更改(默认为0.01)
- RReLU:构造时需要传入两个参数lower和upper,α将是lower和upper间均匀分布的随机数,lower的值默认为1/8,upper的默认值为1/3
- PReLU:斜率α作为一个可优化的值,将在确定权重时一并确定。并且每个元素九可以使用不同的权重值
皱缩激活
皱缩激活用的比较少,这里就先不记了
网络结构的选择
欠拟合与过拟合
欠拟合:由于网络复杂性不够,导致网络不能很好的完成任务
过拟合:网络复杂性过大,导致网络错误地将噪声带来的影响引入到网络中。这样在没有见过的数据中就会引发错误
从左至右分别是欠拟合,正常拟合,过拟合
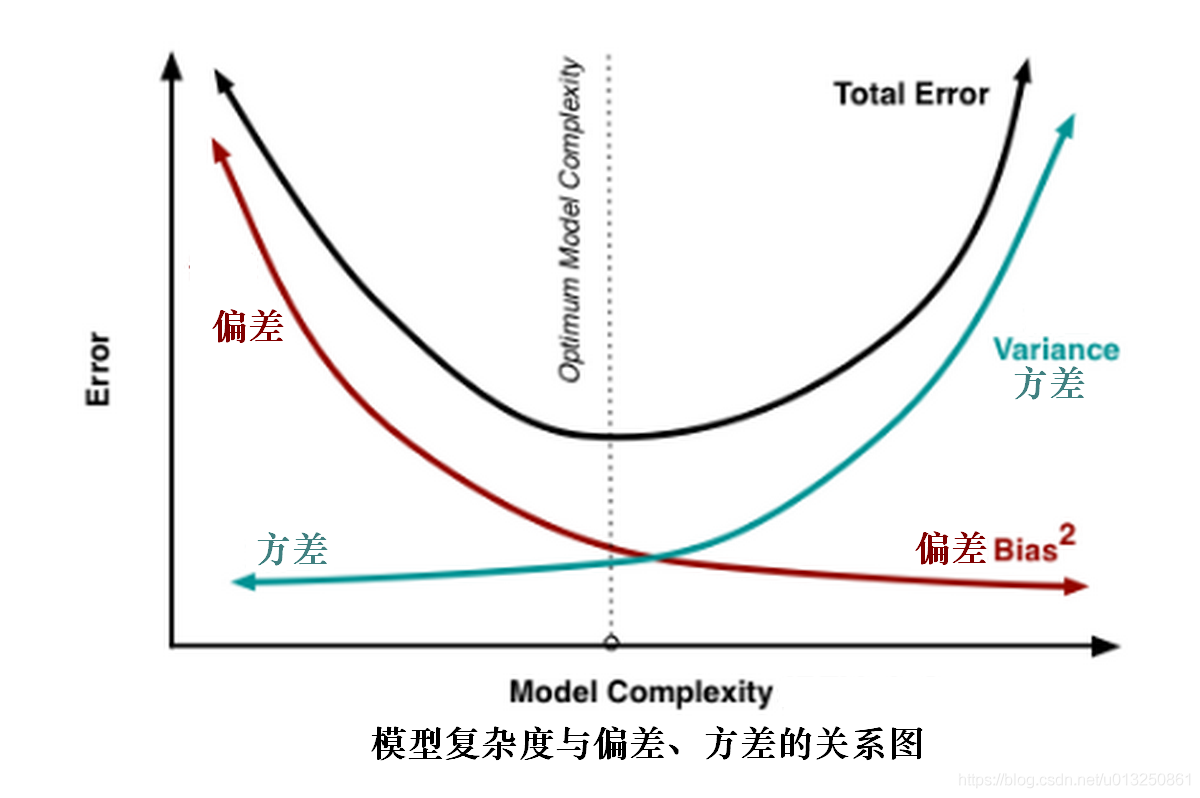
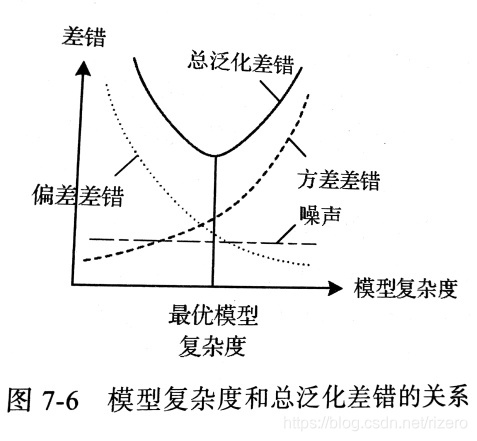
这两种情况都会导致神经网络在新的数据上的性能(又称为“泛化能力”)变差。在给特定训练数据上进行有监督学习得到的网络,在新的数据上难免会出现差错(generalization error)。这里,泛化差错可分为“偏差差错”(bias)、“方差差错”(variance)、“噪声”(noise)。偏差差错是由于网络的缺陷导致网络不能正确完成目标的差错。一般而言,网络越复杂,偏差差错越小。偏差差错过大,就会出现欠拟合。方差差错是由于训练模型使用的数据和新的数据有一定的差别,训练过的网络从训练数据上学习到了在新的数据上并不满足的性质,从而导致差错。一般而言,对于固定的训练数据,网络越简单,方差差错越小。方差差错过大,就会出现过拟合。噪声则是这个系统中没有办法消除的部分。由于方差差错和偏差差错随模型复杂度的变化趋势相反,总泛化差错随着模型复杂度先变小再增大。在理想情况下,应当选择复杂度合适的模型,使得总差错最小,这就需要在偏差差错和方差差错之间进行折中。如果经判断得知当前偏差差错过大,发生了欠拟合,则可以试图通过增加网络层数、每层神经元个数等手段,使得网络变复杂;如果经判断得知当前方差差错过大,发生了过拟合,在训练数据不变的情况下,可以试图通过减小网络层数、每层神经元个数等手段,使得网络变简单。
训练集、验证集和测试集
训练集:用来计算权重值;
验证集:用来判定是否出现欠拟合或者过拟合,并确定网络结构或者控制模型复杂程度的参数
测试集:用来评价最终结果
一般这三者比例是 60%、20%、20%
简单说就是学习的数据越少学习的差错之和也就越小
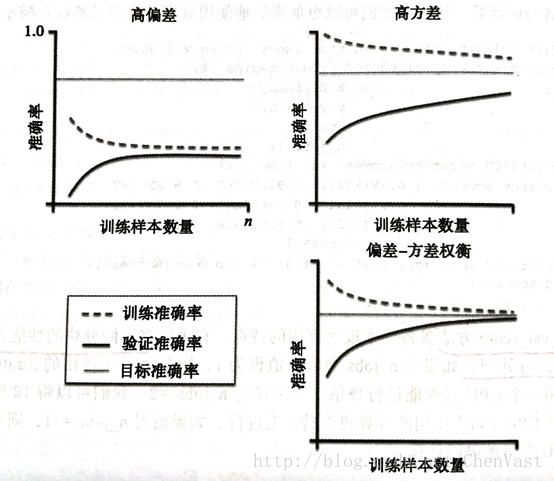
验证曲线:在验证集上的差错随着训练数据条目数的变化称为验证曲线
学习曲线:在训练集上的差错随着训练数据条目数的变化称为验证曲线
偏差方差分析利用验证学习曲线和学习曲线,可以判断网络是否出现了欠拟合或过拟合
- 如果某种结构的网络的学习曲线和验证曲线都收敛到同一个比较大的差错值,通过改大网络可以使得学习曲线和验证曲线收敛到的差错值变小,那么在改大网络前就应该出现了高偏差差错,出现了欠拟合。
- 如果某种结构的网络的学习曲线和验证曲线最终值差别较大,通过改小网络可以使得这个差别变小,那么在改小网络前就应该出现了高方差差错,出现了过拟合。
总结:
| 欠拟合 | 过拟合 | |
|---|---|---|
| 泛化差错主要来源 | 偏差差错 | 方差差错 |
| 模型复杂度 | 过低 | 过高 |
| 学习曲线和验证曲线特征 | 收敛到比较大的差错值 | 两个曲线之间差别大 |
| 解决方案 | 增加模型复杂度 | 减小模型复杂度或增大训练集 |
例子:基于全连接网络的非线性回归
数据生成和数据集分割
import torch
torch.manual_seed(seed=0)# 固定随机数种子,这样生成的数据是确定的
sample_num=1000 # 生成样本数
features=torch.rand(sample_num,2)*12-6 # 特征数据
noises=torch.randn(sample_num)
def himmelblau(x):
return(x[:,0] **2 + x[:,1]-11)**2 +(x[:,0] + x[:,1] **2-7)**2
hims=himmelblau(features)*0.01
labels=hims + noises # 标签数据
train_num,validate_num,test_num=600,200,200 # 分割数据
train_mse=(noises[:train_num] **2).mean()
validate_mse=(noises[train_num:-test_num] **2).mean()
test_mse=(noises[-test_num:] **2).mean()
# MSE算法这里吧预测值当作0,平方的平均值就是数据的MSE
print('真实:训练集MSE={:g},验证集MSE={:g},测试集MSE={:g}'.format(train_mse,validate_mse,test_mse))
输出:
真实:训练集MSE=0.918333,验证集MSE=0.902182,测试集MSE=0.978382
确定网络结构并训练网络
作为开始,我们考虑3层神经网络,前2个隐含层分别有6个神经元和2个神经元,并使用逻辑函数激活;最后一层输出有一个神经元,没有非线性激活,利用torch.nn.Sequential类来搭建这个神经网络
import torch.nn as nn
# 指定隐含层数
hidden_features = [6, 2]
layers = [nn.Linear(2, hidden_features[0]), ]
for idx, hidden_feature in enumerate(hidden_features) :
layers.append(nn.Sigmoid())
next_hidden_feature = hidden_features[idx + 1] \
if idx + 1 < len(hidden_features) else 1
layers.append(nn.Linear(hidden_feature, next_hidden_feature))
print(layers)
net = nn.Sequential(*layers)
print(f'神经网络为{format(net)}')
# 在3.5版本开始,python对星号增加新的适用场景,即在元组、列表、集合和字典内部进行对可迭代参数直接解包,
# 这里需要一再强调的是,这里是在上述四个场景下才可以对可迭代参数直接解包,
# 在其他场景下进行可迭代对象的星号解包操作时不允许的。
输出:
[Linear(in_features=2, out_features=6, bias=True), Sigmoid(), Linear(in_features=6, out_features=2, bias=True), Sigmoid(), Linear(in_features=2, out_features=1, bias=True)]
神经网络为Sequential(
(0): Linear(in_features=2, out_features=6, bias=True)
(1): Sigmoid()
(2): Linear(in_features=6, out_features=2, bias=True)
(3): Sigmoid()
(4): Linear(in_features=2, out_features=1, bias=True)
)
import torch.optim
optimizer = torch.optim.Adam(net.parameters())
criterion = nn.MSELoss()
train_entry_num = 600 # 选择训练样本数
n_iter = 100000 # 最大迭代次数
for step in range(n_iter):
outputs = net(features)
# 去掉所有维度为1的维度
preds = outputs.squeeze()
loss_train = criterion(preds[:train_entry_num], labels[:train_entry_num])
loss_validate = criterion(preds[train_num: -test_num], labels[train_num: -test_num])
if step % 1000 == 0:
print('#{} 训练集MSE = {:g},验证集MSE={:g}'.format(step, loss_train, loss_validate))
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
print(f'训练集MSE = {loss_train}, 验证集MSE={loss_validate}')
输出一部分:
#96000 训练集MSE = 1.04245,验证集MSE=1.06843
#97000 训练集MSE = 1.04209,验证集MSE=1.06864
#98000 训练集MSE = 1.04173,验证集MSE=1.06773
#99000 训练集MSE = 1.04131,验证集MSE=1.0668
训练集MSE = 1.040966510772705, 验证集MSE=1.0663131475448608
outputs = net(features)
preds = outputs.squeeze()
loss = criterion(preds[-test_num:], labels[-test_num:])
print(loss)
输出:
tensor(1.0991, grad_fn=<MseLossBackward0>)