稀疏矩阵存储方式之CSR\CSC
一、前言
维基百科(Wikipedia):
Large sparse matrices often appear in scientific or engineering applications when solving partialdifferential equations. Whenstoring and manipulating sparse matrices on a computer, it isbeneficial and often necessary to use specialized algorithms and data structures that take advantage of the sparse structure ofthe matrix. Operations using standard dense-matrix structures and algorithmsare slow and inefficient when applied to large sparse matrices as processingand memory are wasted on the zeroes. Sparse data is by nature moreeasily compressed and thus requires significantly less storage. Some very large sparse matrices areinfeasible to manipulate using standard dense-matrix algorithms .
大型稀疏矩阵在计算科学以及工程应用中往往应用于求解偏微分方程PDEs。在计算机中存储和操作稀疏矩阵时候,通常需要使用特殊的算法和数据结构以充分发挥矩阵的稀疏性。如果将标准的密集矩阵存储的数据结构和算法用于稀疏矩阵是很慢的并且是低效的,因为大量的计算和存储浪费在零元素上面。因此对于稀疏矩阵的压缩存储很有必要。这里主要介绍稀疏矩阵的存储方式为CSR和CSC。
二、稀疏矩阵存储方式之CSR与CSC
1、Compressedsparse row (CSR, CRS or Yale format)
The compressedsparse row (CSR) or compressed row storage (CRS) format represents a matrix M by three (one-dimensional) arrays, thatrespectively contain nonzero values, the extents of rows, and column indices.It is similar to COO, but compresses the row indices, hence the name. Thisformat allows fast rowaccess and matrix-vector multiplications (Mx).
CSR矩阵压缩:采用三个以为数组表示一个二维矩阵,这个三个以为数组分别是存储非零元素(nozero values)、非零元素的行范围?(the extents of rows)、非零元素的列下标(column indices)。使得矩阵的访问元素以及矩阵的乘法更为快速!
The CSR format stores a sparse m × n matrix M in row form using three (one-dimensional)arrays (A, IA, JA). Let NNZ denote the number of nonzero entries in M.
CSR的三个一维数组分别用A,IA和JA表示,NNZ表示稀疏矩阵M(mxn)的非零元素的个数。A(NNZ个非零元素,nozero values)、IA(the extents of rows)、JA(非零元素的列下标,column indices)。
A: The array A is of length NNZ and holds all the nonzero entries of M in left-to-right top-to-bottom("row-major") order.A数组是一个存储二维M矩阵中NNZ个非零元素的一位数组(这些非零元素依次为从左到右,从上到下)。
IA: The array IA is of length m + 1,IA为一个长度为m+1的一维数组(行数+1).
IA的表示类似一种相对位置表示法,递推公式为:
IA[0] = 0
IA[i] = IA[i − 1]+ (number of nonzero elements on the (i-1)-th row in the originalmatrix). 备注:表示的是IA数组的第i个元素由前一个元素加上在原矩阵中第i-1行的非零元素个数,及存储的是相对偏移量offset,表示某一行的第一个元素在values里面的起始偏移位置。
Thus, the first m elements of IA store the index into A of the first nonzero element in each row of M, and the last element IA[m] stores NNZ, the number of elements in A, which can be also thought of as the index in A of first element of a phantom row just beyondthe end of the matrix M. The values of the i-th row of the original matrix is read from the elements A[IA[i]] to A[IA[i + 1] − 1] (inclusive on both ends), i.e. from the startof one row to the last index just before the start of the next.
含义:前m个元素存储M中每一行的第一个非零元素的索引相对于A数组的第一个元素的偏移量,最后一个元素存储非零元素个数。原矩阵M中的第i行的数值通过从A[IA[i]] 到 A[IA[i + 1] − 1]读取。
JA: The thirdarray, JA, contains the column index in M of each element of A and hence is of length NNZ as well. JA表示非零元素在矩阵M中列索引。
需要注意的是:The CSR format saves on memory only when NNZ < (m (n − 1) − 1) / 2
CSR存储格式满足的必要条件:矩阵非零元素个数NNZ满足: NNZ < (m (n −1) − 1) / 2
2、Compressedsparse column (CSC or CCS)
同理行变列
3、C++代码实现
为了方便这里采用的是eigen矩阵库:
#include<iostream>
#include<vector>
#include<Eigen/Dense>
using namespace Eigen;
using namespace std;
int main() {
//声明矩阵M及其初始化4x4
MatrixXfM(4,4);
M<< 0, 0, 0, 0,
5, 8, 0, 0,
0, 0, 3, 0,
0, 6, 0, 0;
RowVectorXfA; //存储非零元素
RowVectorXiIA; //存储行相关信息
RowVectorXiJA; //存储非零元素列索引号
vector<float> Atmp; //临时存储非零元素
vector<int> JAtmp; //临时存储非零元素列索引
intm = M.rows();
intn = M.cols();
intNNZ = 0;
IA.resize(m+1);
RowVectorXirow_nozeronum(m);
IA(0) = 0;
for (inti = 0; i <m; i++) {
introw_nozeros=0;
for (intj = 0; j < n; j++) {
if (abs(M(i, j))>1e-6) {
Atmp.push_back(M(i, j));
JAtmp.push_back(j);
NNZ++;
row_nozeros++;
}
}
row_nozeronum(i) = row_nozeros;
if (i > 0) {
IA[i] = IA[i - 1] + row_nozeronum[i-1];
}
}
IA[m] = NNZ;
A.resize(NNZ);
JA.resize(NNZ);
for (intk = 0; k < NNZ; k++) {
A[k] = Atmp[k];
JA[k] = JAtmp[k];
}
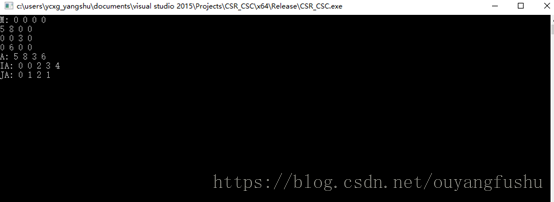
cout<<"M: "<<M<<endl;
cout<<"A: "<<A<<endl;
cout<<"IA: "<<IA<<endl;
cout<<"JA: "<<JA<<endl;
//读取CSR稀疏矩阵数据
getchar();
return 0;
}
维基百科:
https://en.wikipedia.org/wiki/Sparse_matrix#Compressed_sparse_row_.28CSR_or_CRS.29