线索二叉树
线索二叉树的原理
我们把指向前驱和后继的指针称为线索,加上线索的二叉链表称为线索,加上线索的二叉链表为线索链表,相应的二叉树就称为线索二叉树(Threaded Binary Tree)
| lchild | ltag | data | rtag | rchild |
其中:
l ltag为0时指向该结点的左孩子,为1时指向该结点的前驱
l rtag为0时指向该结点的右孩子,为1时指向该结点的后继
实现代码如下:
typedef enum{Link,Thread} PointerTag;
typedef struct BiThrNode
{
TElemType data;
struct BiThrNode *lchild,*rchild;
PointerTag LTag;
PointerTag RTage;
}
线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。由于前驱和后继信息只有在遍历该二叉树时才能得到,所以线索化的过程就是在遍历的过程中修改空指针的过程。
/*中序遍历进行中序线索化*/
BiThrTree pre; //全局变量,始终指向刚刚访问过的结点
void InThreading(BiThrTree p)
{
if(p)
{
InThreading(p->lchild); //递归左子树线索化
if(!p->lchild)
{
p->LTag=Thread
p->lchild = pre;
}
if(!pre->rchild)
{
pre->RTag=Thread;
pre->rchild=p;
}
pre = p; //保持pre指向p的前驱
InThreading(p->rchild); //递归右子树线索化
}
}
除红色部分和二叉公示的中序遍历递归代码几乎完全一样。只不过将本是打印的结点的功能改成线索化的功能。
中间加粗的代码做了这样一些事情if(!p->lchild)表示如果某结点的左指针域为空,因为其前驱结点刚刚访问过,赋值给了pre,所以可以将pre赋值给p->lchild,并修改p-Ltag=Thread(也就是定义为1)完成前驱结点的线索化。
后继就是要稍稍麻烦一些。因为此时p结点的后继还没有访问,因此只能对它前驱结点pre的右指针rchild做判断,if(!pre->rchild)表示如果为空,并且设置pre->RTag=Thread,完成后继结点的线索化。完成前驱和后继的判断后,别忘记将当前的结点p赋值给pre,以便于下一次使用。
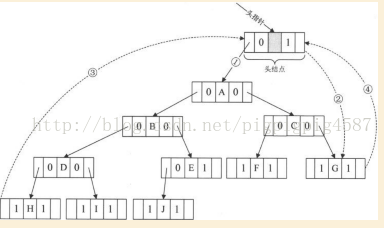
有了线索二叉树后,我们对它的进行遍历时发现,其实就等于是操作一个双向链表结构。
和双向链表结构一样,在二叉树线索链表上添加一个头结点,并令其lchild域的指针指向二叉树的根结点,其rchild域指针指向之前中序遍历时访问的最后一个结点。反之,令二叉树的中序遍历中的第一个结点中,lchild域指针和最后一个结点的rchild域均指向头结点。这样定义的好处就是我们既可以从第一个结点起顺序后继进行遍历,也可以从最后一个结点起顺序前驱进行遍历。
遍历代码如下:
T指向头结点,头结点左链lchild指向根结点,头结点右键rchild指向中高序遍历的最后一个结点,中序遍历二叉线索链表表示的二叉树T
Status InOrderTraverse_Thr(SiThrTree T)
{
BiThrTree p;
p = T->lchild;
while(p!=T)
{
while(p->LTag==Link)
p=p->lchild;
printf(“%C”,p->data);
while(p->RTag==Thread &&p->rchild!=T)
{
p=p->rchild;
printf(“%C”,p->data);
}
p=p->rchild;
}
}