GWO 算法的等级结构

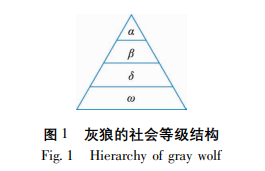
灰狼优化算法是模拟食物链顶端的捕食者狼群的捕食行为产生的算法。灰狼大都喜欢群居， 且具有非常严格的社会等级制度，如图 1 金字塔结 构的等级制度所示。

GWO 算法的数学模型

​ 在 GWO 算法数学建模中，每只灰狼代表种群 中 1 个候选解，将最优解视为 $\alpha$，第二、第三个最佳 候选解视分别为 $\beta$ 和 $\delta$，其余的候选解视为 $\omega$。在 GWO 算法中，搜索( 优化) 由 $\alpha$、$\beta$ 和 $\delta$ 引导，$\omega$ 狼跟随这三只狼。

​ 假设灰狼的种群数量为 $N$，搜索空间为 $Dim$ 维 空间，第 $i$ 只灰狼在第 $Dim$ 维空间中的位置向量可 以表 示 ${X_i}^{Dim}$ 灰 狼围捕猎物的数学模型描述如 式( 4) 、式( 5) 所示:
$$\begin{gathered} D=|C{X}_p(t)-C(t)|(4) \\ X(t+1)=X_p(t)-AD(5) \end{gathered}$$

式(5) 中: $t$ 表示当前迭代次数; $A$ 和 $C$ 为系数向量; $X_p$ 为猎物的位置向量; $D$ 为灰狼个体与猎物之间的位置 关系向量; $X$ 为灰狼的位置向量。$A、C$ 计算公式为
$$\begin{gathered} A=2a{r}_1-a(6) \\ C=2r_2(7) \end{gathered}$$
式中: $r_1$ 和 $r_2$ 的模是$[0,1]$的随机数; $a$ 为收敛因 子，其数值随着迭代次数的增加从 2 线性减小到 0， 计算公式为
$$a=2-\frac{2t}{t_{max}}(8)$$
式( 8) 中: $t$ 为当前迭代次数; $t_{max}$为最大迭代次数。 灰狼追踪猎物位置的数学模型描述如式( 9) ～ 式( 11) 所示:
$$\begin{gathered} D_{\alpha }=|C_1{X}_{\alpha }-X| \\ {D}_{\beta }=|C_2{X}_{\beta }-X|(9) \\ {D}_{\delta }=|C_3{X}_{\delta }-X| \end{gathered}$$
式中: $C_1、C_2、C_3$ 为随机向量; $D_{\alpha }、D_{\beta }$ 和 $D_{\delta }$ 分别为 $\alpha$ 狼、$\beta$ 狼和 $\delta$ 狼与狼群其他成员之间的距离; $X_{\alpha }$、$X_{\beta }$、$X_{\delta }$ 分别为 $\alpha$ 狼、$\beta$ 狼和 $\delta$ 狼的位置; $X$ 为当前狼的位置。 狼群中 $\omega$ 狼的位置由 $\alpha$ 狼、$\beta$ 狼和 $\delta$ 狼共同决定。

灰狼算法的python实现

import random
import numpy

def GWO(objf, lb, ub, dim, SearchAgents_no, Max_iter):
    # 初始化 alpha, beta, and delta_pos
    Alpha_pos = numpy.zeros(dim)  # 位置.形成30的列表
    Alpha_score = float("inf")  # 这个是表示“正负无穷”,所有数都比 +inf 小；正无穷：float("inf"); 负无穷：float("-inf")

    Beta_pos = numpy.zeros(dim)
    Beta_score = float("inf")

    Delta_pos = numpy.zeros(dim)
    Delta_score = float("inf")  # float() 函数用于将整数和字符串转换成浮点数。

    # list列表类型
    if not isinstance(lb, list):  # 作用：来判断一个对象是否是一个已知的类型。 其第一个参数（object）为对象，第二个参数（type）为类型名，若对象的类型与参数二的类型相同则返回True
        lb = [lb] * dim  # 生成[100，100，.....100]30个
    if not isinstance(ub, list):
        ub = [ub] * dim

    # Initialize the positions of search agents初始化所有狼的位置
    Positions = numpy.zeros((SearchAgents_no, dim))
    for i in range(dim):  # 形成5*30个数[-100，100)以内
        Positions[:, i] = numpy.random.uniform(0, 1, SearchAgents_no) * (ub[i] - lb[i]) + lb[i]  # 形成[5个0-1的数]*100-（-100）-100
    Convergence_curve = numpy.zeros(Max_iter)

    #迭代寻优
    for l in range(0, Max_iter):  # 迭代1000
        for i in range(0, SearchAgents_no):  # 5
            # 返回超出搜索空间边界的搜索代理

            for j in range(dim):  # 30
                Positions[i, j] = numpy.clip(Positions[i, j], lb[j], ub[
                    j])  # clip这个函数将将数组中的元素限制在a_min(-100), a_max(100)之间，大于a_max的就使得它等于 a_max，小于a_min,的就使得它等于a_min。

            # 计算每个搜索代理的目标函数
            fitness = objf(Positions[i, :])  # 把某行数据带入函数计算
            # print("经过计算得到：",fitness)

            # Update Alpha, Beta, and Delta
            if fitness < Alpha_score:
                Alpha_score = fitness  # Update alpha
                Alpha_pos = Positions[i, :].copy()

            if (fitness > Alpha_score and fitness < Beta_score):
                Beta_score = fitness  # Update beta
                Beta_pos = Positions[i, :].copy()

            if (fitness > Alpha_score and fitness > Beta_score and fitness < Delta_score):
                Delta_score = fitness  # Update delta
                Delta_pos = Positions[i, :].copy()

        # 以上的循环里，Alpha、Beta、Delta

        a = 2 - l * ((2) / Max_iter);  #   a从2线性减少到0

        for i in range(0, SearchAgents_no):
            for j in range(0, dim):
                r1 = random.random()  # r1 is a random number in [0,1]主要生成一个0-1的随机浮点数。
                r2 = random.random()  # r2 is a random number in [0,1]

                A1 = 2 * a * r1 - a;  # Equation (3.3)
                C1 = 2 * r2;  # Equation (3.4)
                # D_alpha表示候选狼与Alpha狼的距离
                D_alpha = abs(C1 * Alpha_pos[j] - Positions[
                    i, j]);  # abs() 函数返回数字的绝对值。Alpha_pos[j]表示Alpha位置，Positions[i,j])候选灰狼所在位置
                X1 = Alpha_pos[j] - A1 * D_alpha;  # X1表示根据alpha得出的下一代灰狼位置向量

                r1 = random.random()
                r2 = random.random()

                A2 = 2 * a * r1 - a;  #
                C2 = 2 * r2;

                D_beta = abs(C2 * Beta_pos[j] - Positions[i, j]);
                X2 = Beta_pos[j] - A2 * D_beta;

                r1 = random.random()
                r2 = random.random()

                A3 = 2 * a * r1 - a;
                C3 = 2 * r2;

                D_delta = abs(C3 * Delta_pos[j] - Positions[i, j]);
                X3 = Delta_pos[j] - A3 * D_delta;

                Positions[i, j] = (X1 + X2 + X3) / 3  # 候选狼的位置更新为根据Alpha、Beta、Delta得出的下一代灰狼地址。

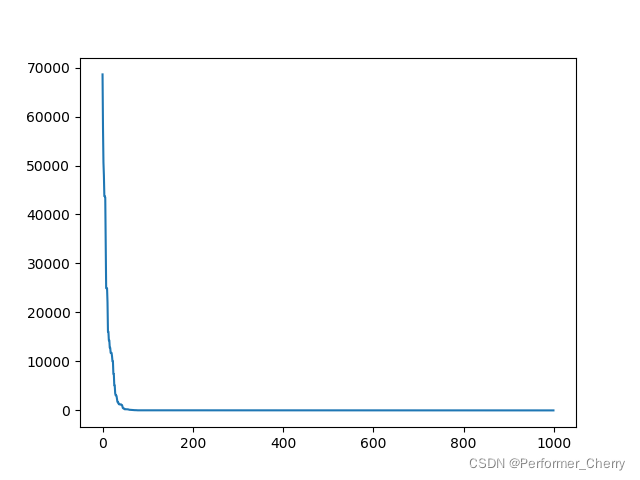
        Convergence_curve[l] = Alpha_score;

        if (l % 1 == 0):
            print(['迭代次数为' + str(l) + ' 的迭代结果' + str(Alpha_score)]);  # 每一次的迭代结果

#函数
def F1(x):
    s=numpy.sum(x**2);
    return s

#主程序
func_details = ['F1', -100, 100, 30]
function_name = func_details[0]
Max_iter = 1000#迭代次数
lb = -100#下界
ub = 100#上届
dim = 30#狼的寻值范围
SearchAgents_no = 5#寻值的狼的数量
x = GWO(F1, lb, ub, dim, SearchAgents_no, Max_iter)

寻优结果

下载链接

完整带图形输出的下载链接（点击可下载）