1. 在C语言中，数字常量如果没有后缀‘U'或'u'，则默认为是有符号数。
例：

其中1024和oxff这两个常量都是有符号数，这就意味着每个赋值操作包含了一个隐式的由有符号数到无符号数的类型转换。
而1024u和0xffu则视为无符号数。

2. 同类型整数之间的类型转换：

这样的类型转换是指不同字长的无符号数或有符号数之间的类型转换，如由short转为int，或是有unsigned short转换为unsigned。
无符号数由短变长使用零扩展，使用0来填充多出来的高字节。
例：

a的二进制表示为1011,0010，b的二进制表示为0000,0000,1011,0010，这就是零扩展。零扩展对于应汇编(ia32)指令movz。

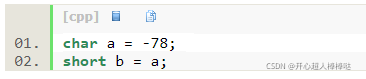
有符号数一般使用补码表示，有符号数的由短变长的转换使用符号扩展，即较短的数的二进制表示的最高位是0则用零扩展，同无符号数的零扩展，而如果是1，则用1来补充缺少的位。
例：

a的二进制表示为1011,0010，b的二进制表示为1111,1111,1011,0010。当然，此时b的大小仍是-78。

而由长变短则更简单，直接截断即可，高位的字节直接丢掉，低位的字节保持不变。

3. 有符号数和无符号数之间进行类型转换：

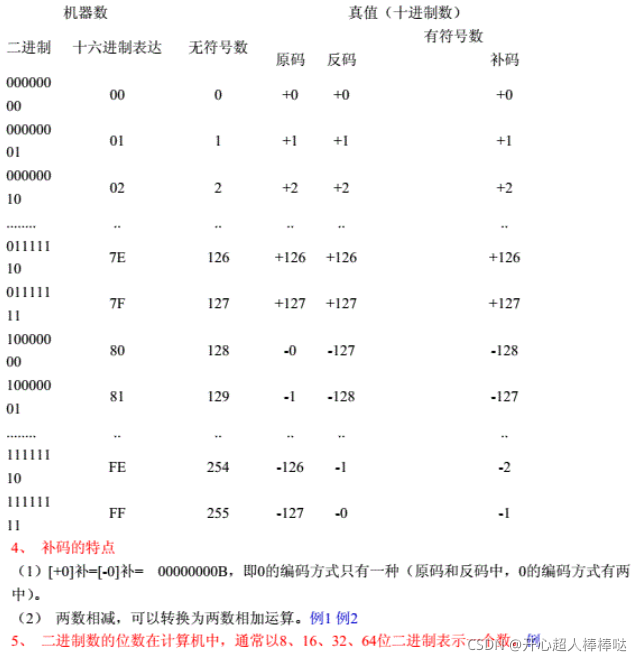
当发生有符号数和无符号数之间的强制类型转换时，如果他们的长度是相同（比如int和unsigned一般都是4个字节，short和unsigned short都是两个字节），那么在位一级的表示上并没有变化，即如果都转化为二进制的形式来看，都是一样的。虽然从二进制01组成的角度来看是一样的，但我们要知道有符号数和无符号数的区别是最高位的权值发生了变化，有符号整数用补码表示，最高位的权值是-2^(w-1)，w为位宽，如int类型w大小为32，而无符号整数的最高为的权值为2^(w-1)。而如果两个数长度不同，则先进行前面提到的2中长度的转换，再进行类型转换。

4. 有符号数和无符号数在一起进行运算时，要首先将有符号数转换为无符号数，再进行运算。

例：

这样可以得到什么结果呢？

首先n转化为无符号数，大小为65535，所以输出是m<n。

本质按位比较，看谁大

5. 整型常量

在1中我们说，如果一个常数没有后缀，那么默认的是int类型，如果后缀是u，则默认为unsigned int。但这样的说法并不完整。

首先，我们默认了常数的格式是十进制，但是十六进制的也很常用。

然后，还可能出现这样的情况：给出的常数的值已经超越了int或是unsigned int的范围。这种情况又该如何处理？

可能目前为止都没有遇到过这种情况，但是如果发生该如何理解呢？别急，C标准对这些情形都给出了明确的说明，了解之后你就会知道为啥不知道也没有发生错误。

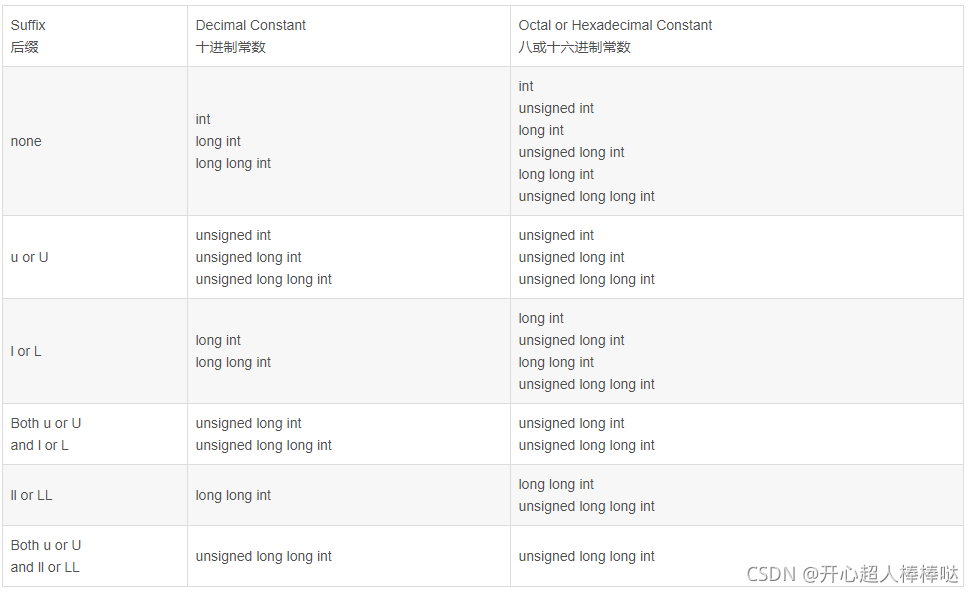
看完下面这张表你也许悟到了点啥，莫名其妙也没关系，让我们来细说一例：

“十进制常数”和“none”后缀的对应的格子里的内容是：

int

long int

long long int

这三行的意思是对于没有后缀的十进制常数，如1024和3147483647，首先用int类型来匹配，int类型值得范围是-2147483648～2147483647（这里可以看出有符号整型的范围不是对称的，而且此处默认int类型为32位），1024在此范围之内，那么这个常数的类型就是int了，但3147483647不在此范围之内，即int类型罩不住，那么看第二行， long int 类型， 其范围还依赖于机器的字长，一般32位机上为-2147483648～2147483647，还是罩不住，再看第三行，long long int，其范围是-9223372036854775808到9223372036854775807，所以3147483647最终匹配的类型是long long int。

对于八进制或十六进制的常数，如果没有后缀，会先匹配有符号数，再匹配无符号数，毕竟从取值的绝对值的范围的角度上看无符号数更广。

如果一个常数大的表中没有任何类型能够表示，那么就要看有没有扩展类型能够表示它，如果没有，那么这个常数没有类型。

-2147483648这个常数会是什么类型？不一定是int类型，这还要看编译器，很可能编译器会把它当成一个64位的有符号整型（可能是long long int），或者说该编译器在识别常数时可能认为int类型的范围是-2147483647～2147483647，但是我们应该知道32位的int类型是可以表示-2147483648。所以求int类型的绝对值也不那么简单，需要考虑这种情况。

我们知道，C代码会被编译为针对某种处理器架构的汇编代码，然后生成机器码，机器码才能够被cpu执行。在C代码时看起来很简单的逻辑，变为机器码后就很难读懂了，也就是说C代码比汇编代码和机器码对人类来说有更好的可读性。我们也知道一般用C语言进行底层开发，如开发Linux操作系统，为什么不用java呢，因为C语言更硬一些，更方便对硬件功能进行抽象描述，C语言在高级语言中并不那么高级。C标准中，整数分为有符号整数和无符号整数，但是归根到底是要放到寄存器中才能进行运算的（所有的高级语言层面抽象出来的数据结构和在这之上的操作，最终都要基于最底层硬件的寄存器、指令等来表现，中间转化过程一般有编译器完成），而寄存器是没有有符号和无符号的属性的，32位cpu上的寄存器由32个二进制位组成，至于其中放的是有符号数还是无符号数，则要看你怎么用它，就如一棵树，你可以把它做成家具，也可以把它当成柴火，要看你的需求。比如我们要将4位的整数1011扩展为8位的整数，如果我们（其实是编译器的工作）认为它是无符号的数，那么可以使用零扩展转移指令，变为00001011；如果认为是有符号，可以使用符号扩展转移指令，变为11111011（补码表示）。如果我们任性的要把4位的有符号的数变为8位无符号的数，也可以，但是要制定统一的规则，比如C标准中有该规定，那么这种转化就是可移植的，如果没有统一的规则，每个编译器都有自己的搞法，这件事就变成了依赖于编译器的事情，这就是所谓的依赖性。所谓的可移植性就是有统一的标准，所谓的不可移植，即依赖性，就是因为大家各搞各的。

参考CSAPP和C99
————————————————
版权声明：本文为CSDN博主「fhyangchina」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/fhyangchina/article/details/55250934